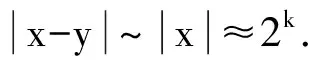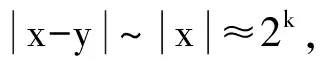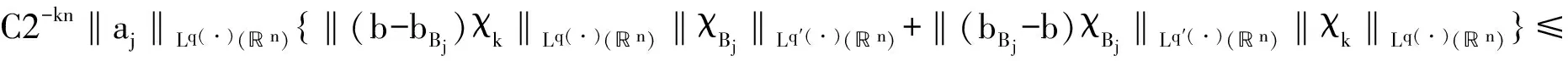Marcinkiewicz积分交换子的BMO估计
2017-05-16王洪彬武怡宏
王洪彬,武怡宏
(1.山东理工大学 理学院,山东 淄博 255049;2.淄博师范高等专科学校 招生就业处,山东 淄博255130)
Marcinkiewicz积分交换子的BMO估计
王洪彬1,武怡宏2
(1.山东理工大学 理学院,山东 淄博 255049;2.淄博师范高等专科学校 招生就业处,山东 淄博255130)
Marcinkiewicz积分交换子由Marcinkiewicz积分算子和BMO函数所生成,是调和分析中的重要算子. 将变指标Herz型Hardy空间上的原子分解定理进行适当推广, 利用其证明了Marcinkiewicz积分交换子在变指标Herz型Hardy空间上的有界性.
Marcinkiewicz积分;交换子;Herz型Hardy空间;BMO
算子的有界性理论一直是调和分析研究的主要课题, 它极大地推动了调和分析与其它学科有机结合的进程.Marcinkiewicz积分交换子是调和分析中的重要算子, 它在调和分析理论中具有重要的地位. 变指标函数空间理论作为调和分析领域的重要理论, 是二十世纪九十年代Kovik和Rákosník在研究具有非标准增长条件的非线性Dirichlet边值问题时提出的[1]. 变指标函数空间不仅从本质上推广了经典函数空间, 而且它与偏微分方程、概率论、弹性力学及流体力学等数学、力学中的多个分支有着非常紧密的联系[2], 已成为近年来调和分析领域最活跃的课题之一. 近些年来,调和分析中的许多重要空间, 如变指标Triebel-Lizorkin空间[3]、变指标Herz空间[4]、变指标Hardy空间[5]和变指标Herz型Hardy空间[6]等相继被建立,对于调和分析中的重要算子及其交换子在上述空间中的研究也取得了一定的成果[7-11]. 本文适当推广变指标Herz型Hardy空间上的原子分解定理,并用它证明Marcinkiewicz积分交换子在此空间中的有界性.
1 预备知识和记号
设Sn-1为n(n≥2)上的单位球面,Ω∈Lipβ(Sn-1)(0<β≤1)是零次齐次函数且满足∫Sn-1Ω(x′)dσ(x′)=0, 其中对任意x≠0有年,Stein[12]定义了如下与Littlewood-Paleyg函数相关的Marcinkiewicz积分算子:,其中,
令b为n中的局部可积函数, 定义由Marcinkiewicz积分算子μ和函数b所生成的交换子为
下面介绍变指标函数空间中的一些知识和记号. 给定开集Ω⊂n及可测函数p(·):Ω→[1,),Lp(•)(Ω)表示Ω上所有可测函数f的集合, 且满足对某个λ>0, 使得p(x)dx<.


在变指标Lp空间中有如下几个重要的引理.
引理 1[1]令p(·)∈P(n). 若f∈Lp(·)(n)且g∈Lp′(·)(n), 则fg在n上可积并且
其中rp=1+1/p--1/p+. 上述不等式被称为广义Hölder不等式.
引理 2[4]设p(·)∈B(n). 则存在常数C>0使得对所有n中的球B, 都有
引理 3[4]令p(·)∈B(n). 则存在正常数C使得对所有n中的球B和所有可测子集S⊂B, 都有

其中δ1,δ2是常数且满足0<δ1,δ2<1(注意在整篇文章中δ1,δ2都同引理3中的一样).
下面给出变指标Herz空间的定义. 对于k∈, 令且Ak=BkBk-1. 记+和分别是所有正整数和所有非负整数的集合, 对k∈有χk=χAk, 若k∈+则且其中χAk是Ak的特征函数.
定义 1[4]令α∈, 0 在此基础上给出变指标Herz型Hardy空间的定义及其原子分解特征. 用S(n)表示n上的Schwartz空间, 它是由无穷可微且在无穷远处迅速递减的函数所构成的,S′(n)表示S(n)的对偶空间. 令GNf(x)为f(x)的grand极大函数, 其定义为,其中且是非切向极大算子并且其定义为其中φt(x)=t-nφ(x/t). 定义 2[6]令α∈, 0 对于x∈我们用[x]表示小于等于x的最大整数. 由文献[6]中的结论容易得到 定义 3 令α∈,q(·)∈P(n)且非负整数s≥[α-nδ2].n上的函数a被称为中心(α,q(·))-原子, 如果它满足(i) 对某个r>0有suppa⊂B(0,r);; (iii) 对任意满足的多重指标β有∫a(x)xβdx=0.n上的函数a被称为是限制型中心(α,q(·))-原子, 如果它满足上述条件(ii), (iii)以及对某个r≥1有suppa⊂B(0,r). 注:在定义3中若对某个k∈有r=2k, 则称相应的中心(α,q(·))-原子为二进中心(α,q(·))-原子. 引理 4[6]令α∈, 0 引理 5[13]令k是正整数, 则对所有b∈ΒΜΟ(n)和所有j,i∈满足j>i, 有 ‖(b-bBi)kχBj‖Lp(·)(n) 其中B是n中的球. 文献[14]给出了Marcinkiewicz积分交换子[b,μ]的Lp(•)(n)有界性,下面将其推广到变指标Herz型Hardy空间中. 定理1 令b∈BΜΟ(n),q(·)∈B(n), 0 (1) 首先估计I2. 由[b,μ]的Lq(·)(n)有界性有 (2) 下面估计I1. 由aj的消失矩条件得 (3) 因为Lipβ(Sn-1)⊂L(Sn-1), 所以通过(3)式, Minkowski不等式和广义Hölder不等式有 所以有 由引理2、引理3和引理5, 有 ‖[b,μ](aj)χk‖Lq(·)(n)≤ C2-kn‖aj‖Lq(·)(n)(k-j)‖b‖*‖χBk‖Lq(·)(n)‖χBj‖Lq′(·)(n)≤ (4) 因此, 有 当1 (5) 当0 (6) 类似于对J1的估计, 得 类似于对J2的估计, 得 所以有 由引理2、引理3和引理5,有 ‖[b,μ](aj)χk‖Lq(·)(n)≤ C2-jn‖aj‖Lq(·)(n)(j-k)‖b‖*‖χBk‖Lq(·)(n)‖χBj‖Lq′(·)(n)≤ (7) 因此, 有 当1 (8) 当0 (9) 结合式(1), (2), (5), (6), (8)和(9), 有 因此, 定理1得证. [1]KOVJ.OnspacesLp(x)andWk,p(x)[J].CzechoslovakMathJ, 1991, 41(4): 592-618. [2]DIENINGL,HARJULEHTOP,HSTÖP,etal.LebesgueandSobolevspaceswithvariableExponents[M].Heidelberg:Springer, 2011. [3]XUJS.VariableBesovandTriebel-Lizorkinspaces[J].AnnAcadSciFennMath, 2008, 33: 511-522. [4]IZUKIM.BoundednessofsublinearoperatorsonHerzspaceswithvariableexponentandapplicationtowaveletcharacterization[J].AnalMath, 2010, 36(1): 33-50. [5]NAKAIE,SAWANOY.HardyspaceswithvariableexponentsandgeneralizedCampanatospaces[J].JFunctAnal, 2012, 262(9): 3 665-3748. [6]WANGHB,LIUZZ.TheHerz-typeHardyspaceswithvariableexponentandtheirapplications[J].TaiwaneseJMath, 2012, 16(4): 1 363-1 389. [7]WANGHB.CommutatorsofMarcinkiewiczintegralsonHerzspaceswithvariableexponent[J].CzechoslovakMathJ. 2016, 66(1): 251-269. [8]WANGHB.BoundednessofcommutatorsonHerz-typeHardyspaceswithvariableexponent[J].JordanJMathStat, 2016, 9(1):17-30. [9] 王洪彬.变指标Herz型Hardy空间上的Marcinkiewicz积分[J]. 山东理工大学学报(自然科学版), 2015, 29(4): 16-20. [10] 王洪彬.变指标Herz型Hardy空间上一类交换子的有界性[J]. 山东理工大学学报(自然科学版), 2015, 29(3): 27-31. [11] 王洪彬.变指标Herz型Hardy空间上的齐性分数次积分[J]. 鲁东大学学报(自然科学版), 2015, 31(2): 107-111. [12]STEINEM.OnthefunctionofLittlewood-Paley,LusinandMarcinkiewicz[J].TransAmerMathSoc, 1958, 88(2): 430-466. [13]IZUKIM.BoundednessofcommutatorsonHerzspaceswithvariableexponent[J].RenddelCircoloMatediPalermo, 2010, 59(2):199-213. [14] 王洪彬,傅尊伟,刘宗光. 变指标Lebesgue空间上的Marcinkiewicz积分高阶交换子[J]. 数学物理学报, 2012, 32A(6): 1 092-1 101. (编辑:郝秀清) BMO estimate for the commutators of Marcinkiewicz integrals WANG Hong-bin1, WU Yi-hong2 (1.School of Science, Shandong University of Technology, Zibo 255049, China;2. Department of Recruitment and Employment, Zibo Normal College,Zibo 255130,China) The commutator of Marcinkiewicz integral, which is generated by the Marcinkiewicz integral and BMO function, is very important in harmonic analysis. Using the extended atomic decomposition characterizations of Herz-type Hardy spaces with variable exponent, we obtain the boundedness of the commutator of Marcinkiewicz integral on the Herz-type Hardy spaces with variable exponent. Marcinkiewicz integral;commutator;Herz-type Hardy space;BMO 2016-06-11 国家自然科学基金项目(11171345);山东省自然科学基金项目(ZR2015PA001) 王洪彬, 男,wanghb@sdut.edu.cn 1672-6197(2017)04-0024-06 O A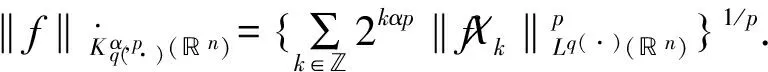


2 主要结论及证明