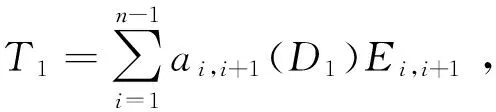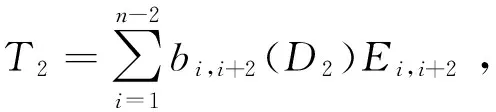交换环上上三角矩阵李代数的李三次导子

周丽丽

(晋中学院数学系，山西 晋中 030600)

交换环上上三角矩阵李代数的李三次导子

周丽丽

(晋中学院数学系，山西 晋中 030600)

为进一步研究导子，给出了李三次导子的概念，并利用其在矩阵基上的作用, 将含有单位元的交换环上上三角矩阵李代数的任意一个李三次导子分解为内三次导子、中心三次导子之和, 推广了导子的概念.

上三角矩阵李代数; 导子; 李三次导子; 交换环

引言

设R为含单位元的交换环,L为R上的李代数. 对任意的X,Y∈L，若存在一个映射φ：L→L,有φ([X,Y])=[φ(X),Y]+[X,φ(Y)], 则称φ为L上的一个导子.

导子在现代数学的研究中,发挥了不可缺少的作用.例如在20世纪40年代，Picard和Vessiot就是利用导子这个工具发现代数方程的Galois理论可以转化为通常的线性微分方程的理论.近几十年来，关于导子及导子推广的课题不断提出，大量的结论不断涌现,参看文献[2]～[11].本文给出了李代数上李三次导子的概念，它是导子概念的另一种推广，并进而决定了含有单位元的交换环上上三角矩阵李代数的所有李三次导子的具体形式.

1 基本概念和主要定理

设R是含有单位元的交换环,L是R上的李代数,φ:L→L是一个映射,且对任意的X,Y,Z∈L, 有

φ([[X,Y],Z])=[[φ(X),Y],Z]+[[X,φ(Y)],Z]+[[X,Y],φ(Z)]

则称φ为L上的李三次导子.

从而易见, 当φ是L上的导子时, 它必定是L上的李三次导子，故李三次导子概念是导子概念的一种推广.但是反过来, 却不一定成立.以下例子说明了这点.

例 1 设Nn(R)为含幺环上严格上三角矩阵组成的李代数，

可以验证这是Nn(R)的一个李三次导子，但它不是导子.

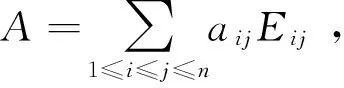
设N1=N,N2=[N,N1],N3=[N,N2],…则它们为N的降中心链, 且每一Nk都为Tn(R)的理想.

对大于1的正整数n, 设1≤k≤n-1, 则存在两个非负整数q、r，且r≤k-1，使得n=kq+r, 令Dk=Diag(Ek,2Ek,…,qEk,(q+1)Er)∈Dn(R),k=1,2,…,n-1.式中Ek为k×k单位矩阵.如果r=0，则令Dk=Diag(Ek,2Ek,…,qEk).

现在构造Tn(R)的几个标准的李三导次子.

1) 内三次导子

对任意的X∈Tn(R),那么映射adX:Tn(R)→Tn(R),Y[X,Y]是由X诱导的Tn(R)的一个导子, 称它为内三次导子.

2) 中心三次导子

φ(D+X)=(D)E,∀D∈Dn(R),X∈Nn(R)

可以证得φ是Tn(R)上的一个李三次导子, 称其为由诱导的中心三次导子.

主要定理：

定理1 设R是含有单位元的交换环，Tn(R)为其上的n阶上三角矩阵组成的李代数.若映射φ:

Tn(R)→Tn(R)为Tn(R)上的李三次导子，则φ=adT+φ，其中adT为内三次导子,φ为中心三次导子.

2 主要定理的证明

下面分三步来证明定理1.

第一步: 设φ为Tn(R)上的李三次导子, 对任一个对角矩阵H∈Dn(R), 存在上三角矩阵T∈Tn(R),有(φ-adT)(H)∈Dn(R).

对任意的H∈Dn(R), 假设

因[D1,[D1,H]]=0,用φ作用于两端，可得：

[φ(D1)，[D1,H]]+[D1,[φ(D1),H]]+[D1,[D1,φ(H)]]=0

由于[φ(D1),[D1,H]]=0，进而有[D1,[H,φ(D1)]]=[D1,[D1,φ(H)]],因此

比较等式两端,对任意的1≤i

(i(H)-j(H))aij(D1)=(i(D1)-j(D1))aij(H)

取j=i+1,有：(i(H)-i+1(H))ai,i+1(D1)=(i(D1)-i+1(D1))ai,i+1(H).

ai,i+1(H)=(i+1(H)-i(H))ai,i+1(D1),i=1,2,…,n-1

φ(H)∈Dn(R)+N2.若n=2, 则定理的证明已完成; 若n>2,对任意的H∈Dn(R),可设

由[D2,[D2,H]]=0, 可得：

[φ(D2),[D2,H]]+[D2,[φ(D2),H]]+[D2,[D2,φ(H)]]=0

由于[φ(D2),[D2,H]]=0,进而有[D2,[H,φ[D2]]=[D2,[D2,φ(H)]]

因此可得：

比较等式两端,对任意的1≤i

(i(H)-j+1(H))bi,j+1(D2)=(i(D2)-j+1(D2))bi,j+1(H),

取j=i+1,有

(i(H)-i+2(H))bi,i+2(D2)=(i(D2)-i+2(D2))bi,i+2(H).

bi,i+2(H)=(i+2(H)-i(H))bi, i+2(D2),i=1,2,…,n-2

φ(H)∈Dn(R)+N3，若n=3,定理的证明已完成.

若n>3,重复上述步骤,经过n-2步,可设φ(H)∈Dn(R)+Nn-1.对任意的H∈Dn(R), 设：

φ(H)≡C1,n(H)E1,n(mod(Dn(R)),C1,n(H)∈R

同理由[Dn-1,[Dn-1,H]]=0, 可得：

[φ(Dn-1),[Dn-1,H]]+[Dn-1,[φ(Dn-1),H]]+[Dn-1,[Dn-1,φ(H)]]=0

由于[φ(Dn-1),[Dn-1,H]]=0,进而有[Dn-1,[H,φ[Dn-1]]=[Dn-1,[Dn-1,φ(H)]]，

因此可得:

(1(H)-n(H))(1(Dn-1)-n(Dn-1))c1,n(Dn-1)=

(1(Dn-1)-n(Dn-1))(1(Dn-1)-n(Dn-1))c1,n(H)

取Tn=c1,n(Dn-1)E1,n.则(φ-adTn)(H)∈Dn(R). 记T=T1+T2+…+Tn,则(φ-adT)(H)∈Dn(R). 记φ1=φ-adT, 则φ1(H)∈Dn(R).

第二步： 对任意的H∈Dn(R), 若φ1(H)∈Dn(R), 则存在H0∈Dn(R), 对任意的1≤i

对任意的1≤i

取D∈Dn(R), 使得i(D)-j(D)=0, 则有：

气象站位于甘肃酒泉市金塔县境内，地处东经98°30'00"，北纬 40°19'58.8"，北靠黑山，地处戈壁，地势平坦，场地开阔。金塔县位于甘肃省河西走廊中段北部边缘，东、北与内蒙古额济纳旗毗连，西面与甘肃嘉峪关、玉门、肃北接壤，南与酒泉市和张掖地区的高台县为邻。

[D,[D,Eij]]=(i(D)-j(D))(i(D)-j(D))Eij=0

用φ1作用等式两端可得：

[φ1(D),[D,Eij]+[D,[φ1(D),Eij]]+[D,[D,φ1(Eij)]]=0

进一步可得：

(φ1-adH0)(Ei,i+1)=0. 记φ2=φ1-adH0. 则有：

φ2(Ei,i+1)=0,i=1,2,…,n-1

φ2(Eij)=bijEij,j=i+2,…,n

对任意的H∈Dn(R)，有[H,[H,Ei,i+1]]=(i(H)-i+1(H))2Ei,i+1,用φ2作用于两端可得：

2(i(H)-i+1(H))(i(φ2(H))-i+1(φ2(H)))Ei,i+1=0

由于H的任意性,故i(φ2(H))-i+1(φ2(H))=0,所以φ2(H)=rHE,rH∈R.

当n≥3时,由[[Ei,i+1,Ei+1,i+2],H]=(i+2(H)-i(H))Ei,i+2，用φ2作用于两端可得φ2(Ei,i+2)=0.

当1≤k

φ2(Ekl)=0.

故对任意1≤i

第三步:对任意的H∈Dn(R)，存在φ，使得(φ2-φ)(H)=0.

由第二步知,∀H∈Dn(R),φ2(H)=rHE.取=rH,则(H)=rH.故存在φ,使得

(φ2-φ)(H)=0,记φ3=φ2-φ.

综上,对任意的1≤i≤j≤n,有φ3(Eij)=0.从而φ3=0.故φ=adT+φ.

[1]JφndrupS.Automorphismsandderivationsofuppertriangularmatrixring[J].LinearAlgebraAppl, 1995, 221: 205-218.

[2]WangDengyin,YuQiu,OuShikun.DerivationsofcertainLiealgebrasofuppertriangularmatricesovercommmutativerings[J].JournalofMathematicalResearchandExposition, 2007, 27(3): 474-478.

[3]WangDengyin,YuQiu.DerivationsoftheparabolicsubalgebrasofthegenerallinearLiealgebraoveracommutativering[J].LinearAlgebraAppl, 2006, 418: 763-774.

[4]LarsonDR,SourourAR.LocalderviationsandlocalautomophismsofB(H)[J].ProcSymposPureMath,1990, 51: 187-194.

[5]KadisonR.LocalDerivations[J].JAlgebra, 1990,130:494-509.

[6]ChrlstR.LocalDerivationsonOperatorAlgebras[J].JFunctAnal,1996,135:76-92.

[7]LegerGF,LuksEM.GeneralizedderivationsofLiealgebras[J].JAlgebra, 2000, 228:165-203.

[8]张清华,王登银,周津名.可换环上严格上三角矩阵李代数的BZ导子[J].数学杂志,2011,31(1)：55-61.

[9]关琦,卞洪亚,陈炳凯.可换环上严格上三角矩阵李代数的拟导子[J].常熟理工学院学报, 2011(10)：42-47.

[10]周丽丽.可换环上上三角矩阵李代数的括积零导子[J].滨州学院学报， 2015(4)：68-72.

[11]周丽丽,李娜娜,孔祥源.可换环上上三角矩阵李代数的拟导子[J].滨州学院学报， 2013(3)：67-72.

[12]郭文杰. 交换环上反对称李代数的BZ导子[D]. 大连:大连理工大学,2012.

[13]李彩红.算子代数上的ξ-Lie可导映射[D].西安：陕西师范大学，2011.

[14]郑克礼.李超代数的若干结构与表示[D].长春：东北师范大学,2014.

Lie Triple Derivations of the Lie Algebra of Upper Triangular Matrice over Commutative Rings

ZHOU Li-li

(Department of Mathematics, Jinzhong University, Jinzhong Shanxi 030600, China)

For the further study of derivations, the paper gives the concept of Li triple derivations and uses its effect in the matrix basis to decompose any triple derivation of Lie algebras of triangular matrices over commutative rings with unit elements into the sum of three inner derivations and the central three derivations, which generalizes the concept of derivations.

Lie algebra of upper triangular matrices; derivations; Lie triple derivation; commutative rings

1673-2103(2017)02-0001-04

2016-11-20

周丽丽(1985-)，女，山东菏泽人，助教，硕士，研究方向：代数及应用.

O152.5

A