一种检测特征引导的飞机零件模型配准方法*

陈 磊，黄 翔，曾 琪

（1.南京航空航天大学机电学院，南京 210016；2.上海飞机制造有限公司，上海 200436）

随着复杂曲面零件在飞机制造领域的广泛应用，数字化检测技术在保证飞机复杂零件的尺寸测量精度方面发挥着重要作用。测量模型与理论数模（CAD模型）的精确匹配是误差检测分析的重要前提，由于数字化测量设备的测量坐标系与CAD模型的设计坐标系不统一，实现点云模型与CAD模型的位姿配准已成为数字化检测技术的关键。

通常，根据被测物的CAD模型是否已知，可将位姿配准大致分为两类，CAD模型未知的点云重构配准和CAD模型已知的模型引导配准。本文针对零件CAD模型已知的情况开展研究，通过求解满足特定配准要求的最佳刚性变换，实现检测点云与理论数模的准确配准。Meng等[1]研究了CAD模型引导的定位配准方法，并给出模型配准误差的评定方法。王东霞等[2]将粒子群优化算法融入ICP配准，实现被测曲面与设计曲面精确定位。迭代最近点（Iterative Close Point, ICP）算法[3]是模型配准中应用较为广泛的方法，但是基于最小二乘原理的ICP算法在模型配准应用中求解速度慢，配准可靠性差，尤其当实测零件存在局部变形时，配准结果不理想[4-5]。针对ICP配准算法的不足，普遍解决方式是利用特征信息适当简化点云，再进行配准计算。点云简化常用的特征信息包含法向量分布[6]、曲率分布[7]、边界特征[8]等简单特征。由于复杂零件的几何特征差异明显，多数情况下，不能保证不同特征点在简化过程中合理保留，影响配准精度和效率。考虑到零件配准的功能要求，文献[9]依据叶片型面不同区域具有不同公差设计要求的特点，在ICP算法基础上提出了一种区域公差约束的配准方法，尽可能将模型配准控制点集约束在公差带以内。文献[10]利用最大熵原理解决基于加工定位和质量检测的配准问题。文献[11]和[12]则针对数控加工工艺特点，研究了加工余量约束条件下测量数据与CAD模型的配准方法。

ICP算法的配准运算时间大部分消耗在寻找对应最近点集上，而三维激光扫描测得的曲面点云模型数据量级在106～108，且大量的点云并不能明显提高配准精度，因此，在保证配准精度的前提下，减少对应最近点的数量以减少迭代搜索时间，提高ICP算法的配准速度。飞机零件通常是自由曲面或直线、平面、圆柱面、球面等基本几何特征的组合，其特征的几何性质可以由离散的关键特性点来拟合，有鉴于此，本文将能表达产品理论形状的关键特性点定义为产品CAD模型的检测特征点，并以CAD模型的目标匹配点集为引导，采用改进的ICP算法寻找点云模型数据集中与目标匹配点最近的点集，从而提高点云模型与CAD模型的配准效率和精度。

问题描述

对于CAD模型引导测量的零件精度评定，关键是寻找坐标变换矩阵T使零件的测量模型和CAD理论模型配准对齐，实现不同坐标系的匹配统一。假设测量数据中参与配准运算的点为Pi（i=1，2，…，m），对应的CAD模型目标匹配点为Si（i=1，2，…，m），坐标系匹配后，Pi（i=1，2，…，m）在CAD模型上的投影点为Pi'（i=1，2，…，m），则配准过程就是使Pi在CAD模型上的投影点Pi'与对应的目标匹配点Si之间的距离之和最小，其目标函数为：

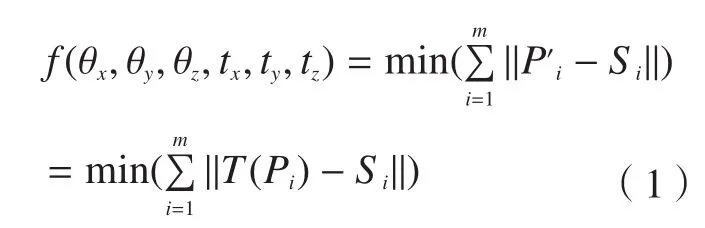
式中，T（Pi）为对Pi进行坐标变换的结果，变换矩阵T是参数向量[R，t]的函数，R=（θx，θy，θz）表示测量模型绕X、Y和Z轴旋转的角度，t=（tx，ty，tz）表示测量模型沿着X、Y和Z轴方向的平移分量。

由此可见，CAD模型引导的配准问题求解的实质是通过优化算法寻找参数（θx，θy，θz，tx，ty，tz），使得式（1）表达的目标函数取得最小值。

CAD模型的目标匹配点规划

对于CAD模型引导的配准求解而言，过多的目标匹配点会增加运算量，且对配准精度的提高并不明显，过少的目标匹配点则难以保证配准结果的可靠性。因此，在保证配准精度的前提下，需在CAD模型上选择尽可能少的特征点作为目标匹配点，以减少配准迭代计算，提高配准效率。鉴于直线、平面、圆柱面、球面、自由曲面等几何特征是反映零件关键特性的主要特征元素，本文通过建立检测特征点的选取规则来选取CAD模型的特征点，并根据模型配准的可靠性分析指标，规划出合理的目标匹配点集，以此提高配准运算效率并保证配准结果的可靠性。

1 检测特征点的选取策略

根据文献[13]研究成果，假设预先指定各个几何特征的检测特征点数目为L，则检测特征点的选取策略为：

（1）线段：把线段细分为3L-2等长的小段，然后在第 1，4，7，…，（3L-2）段中随机采点。

（2）平面：将平面的最大矩形包络细分为L1×L2的小矩形，L1×L2近似等于L，小矩形应尽可能接近于正方形，然后在每个小矩形上随机取一点，同时需保证所取测点在被测平面内。

（3）圆：把圆等分为L个相等的弧段，然后在每个弧段中随机取一点。

（4）球：对于半径为r的球，球面被一簇相距为h的平面所截，测点均匀分布在lc个平行且等距的球横截面圆周上。其中，均匀间隔的平面数，平面与球相交的圆上的均布测点数

（5）圆柱：对于高为h，半径为r的圆柱，测点均匀分布在lc个平行且等距的圆柱横截面圆周上，其中等距的横截面数目每个横截面圆周上的均布测点数lp=[L/lc]。

（6）圆锥：对于高为h，母线长为d，两端半径为r1、r2（r2>r1）的圆锥，测点均匀分布在lc个平行且等距的圆锥横截面圆周上，其中等距的横截面数目为

每个横截面圆周上的均布测点数为：

（7）自由曲面：将自由曲面剖分为L个3角片，取每个三角片的重心为测点。

由此，可利用CAD软件系统（如CATIA，UG等）提供的相关数据接口获取零件的检测信息和对应的关联几何特征，再根据本文中所采用的选取策略确定检测特征点的分布，作为目标匹配点的候选点集。

2 目标匹配点的可靠性分析

由于点云测量数据中包含制造误差和测量误差，使得点云模型与CAD模型的配准结果可靠性差。因此，本文以文献[14]中的配准可靠性指标为基础，在满足配准结果可靠性要求的前提下，确定CAD模型上的目标匹配点集。

模型配准运算得到模型配准最佳变换T*=（R*，t*），CAD模型上参与配准运算的目标匹配点记为Si*（i=1，2，…，L），此时，配准目标函数f在模型配准最佳变换T*下取得最小值ε*。由于每个配准点的配准误差近似服从正态分布，对目标函数f可采用F检验方法作统计检验。

取统计量：U=εa/ε*

式中，εa为配准目标函数f在实际变换下的值。

从统计学可知，U遵从第一自由度和第二自由度都为l=L-6的F分布，则给定置信度α，可推导出由X、Y、Z3个坐标轴方向的平移变换误差δt=（δtx，δty，δtz）T引起的配准平移位置误差的上界估计为：

式中，为置信度α对应的临界值，λt为矩阵Jt的最小特征值，Jt=式中，nt为目标匹配点处的曲面法矢量。

一般将X、Y、Z3个坐标轴的旋转变换误差δθ=（δθx，δθy，δθz）T等效为绕单位向量ω的旋转角度θ，则配准旋转角度θ的上界估计为：

式中，λr为矩阵Jr的最小特征值，其中，qi=Ra Pi，Pi为第i个目标匹配点的对应测量坐标，Ra为测量坐标系相对于CAD模型设计坐标系的旋转矩阵。

式（2）、式（3）定量检验配准点的位置和数目对模型配准可靠性的影响程度，则可被采用作为描述配准结果可靠性的度量指标。利用配准可靠性指标对目标匹配点的候选点集进行优化选择，在CAD模型上筛选出满足配准可靠性要求的目标匹配点集，具体过程如下：

步骤1：设CAD模型上检测特征点的总数为ψ，定置信度α、平移位置误差上界阈值和旋转角度误差上界阈值。

步骤2：按照检测特征点选取策略，建立目标匹配点的候选点集，并按式（2）、（3）计算当前平移位置误差d和旋转角度误差θ。

步骤3：若d

步骤4：ψ=ψ-1，若ψ-6 < 0，则转步骤5；否则，转步骤2。

步骤5：输出筛选后的目标匹配点集

模型配准

为实现测量模型与CAD模型的精确配准，以式（1）为目标优化函数，采用奇异值分解与最近点迭代相结合的配准算法（Singular Value Decomposition Iterative Closest Point，SVD-ICP）求解模型配准的全局最优解。具体求解过程如下：

步骤1：通过粗配准将测量模型的每个点Pi变换到CAD模型坐标系得到点，变换后的测量数据集为，此时旋转矩阵为R0、平移矩阵为T0。

步骤2：设置迭代计数器k=1，测量数据集和目标匹配点集的精确配准旋转矩阵Rk为正交矩阵和平移矩阵T k为0矩阵。

步骤3：寻找测量数据集中与按照目标匹配的可行性分析获得的CAD模型目标匹配点集最近的点集，得到精确匹配点对precise_match=

步骤4：计算精确匹配点对各点集的重心：，并对两点集作相对于各自重心的重合平移：

步骤5：计算测量数据集和目标匹配点集构造的协方差矩阵：

步骤6：根据文献[15]，由协方差矩阵H构造式（4）的四维对称矩阵H'4×4。

步骤7：求解H'4×4的特征值和特征向量，其中最大特征值对应的特征向量为旋转四元数ω=（ω1，ω2，ω3，ω4）T。

步骤8：根据式（5）计算得到旋转矩阵Rk，以及公式Tk=μ'-Rkμ解得平移矩阵T k。

步骤9：终止条件判断：计算本次和最近一次迭代变换后测量数据与CAD模型的匹配误差量Δ，如式（6）所示，若满足Δ<ζ，则迭代结束并转步骤10；否则令k=k+1，并转步骤3。其中ζ为预先设置的阈值。

步骤10：将粗配准的旋转矩阵R0和平移矩阵T0、精配准的旋转矩阵Rk和平移矩阵Tk共同作用于测量模型，即为最终的配准结果。

实例分析与验证

为分析不同目标匹配点集对配准结果的影响，以某型飞机翼肋的CAD模型为基础，在零件型面上以较高密度离散出5000个数据点，并对这些数据点施加已知的旋转和平移变换，然后对数据点添加随机噪声的仿真数据作为零件型面的实际测量数据，结果如图1所示，具体参数设置见表1。

图1 零件型面离散点Fig.1 Discrete points of part surface

分别用均匀采样方法和前文的检测特征点选取策略，确定CAD模型上的目标匹配点集S1、S2（点数N1=N2=300），如图2中的（a）、（b）所示。利用目标匹配点的可靠性分析给出的可靠性分析方法对检测特征点集S2进行筛选（设定平移位置误差和旋转角度误差的置信度均为97%），将筛选出的数据点作为目标匹配点集S（3N3=164），结果如图 （2c）所示。

为便于直观地评价配准精度，设测量数据与CAD模型匹配后，测量数据中任意一点在CAD模型上的投影点与对应目标匹配点之间的距离为，则配准误差为

测量数据与3种不同目标匹配点集的配准结果如表2所示，3种目标匹配点集的配准精度的差值小于0.001mm，说明在目标匹配点数量足够的情况下，增加目标匹配点的数量对模型配准精度不会有明显提高。并且以S3为目标匹配点集的计算耗时最短，由此可见通过目标匹配点的布局优化在改善配准精度的同时，可以明显提高配准的计算效率。

在应用试验中，使用ATOS三维光学扫描仪检测实际零件得到测量数据，并在Visual Studio 2010编程环境下实现模型配准算法。本文使用的测量系统为ATOS Compact Scan 5M，其单次扫描的测量点数可达106个，测量时间约0.8s，点距分辨率为0.017～0.481mm，测量精度可达0.01mm。

测量数据与CAD模型进行配准时，分别采用均匀采样方法和结合配准可靠性分析的检测特征点选取策略（设定平移位置误差和旋转角度误差的置信度均为97%），确定CAD模型上的目标匹配点集S1'、S2'（点数N1=700、N2=267）。根据模型配准提出的方法进行配准，计算得到配准误差以及平移参数与旋转参数的误差上限如表3所示。

从表3可以看出，以检测特征点作为目标匹配点集的配准结果比均匀采样的目标匹配点集的配准结果的精度高，主要原因是零件的检测特征通常处于零件成形过程的易变形区域，而采用本文介绍的检测特征点选取策略获得的目标匹配点集会在该区域侧重地分布较多匹配点，有利于提高配准精度。此外，目标匹配点集S2'经过筛选参与模型配准，提高了配准结果的可靠性，可避免由于零件变形过大导致的模型配准失败。

表1 仿真数据设置参数

图2 不同目标匹配点集Fig.2 Different target matching point sets

表2 3种目标匹配点集的配准结果

表3 不同目标匹配点集的配准误差对比

结束语

本文提出了一种检测特征引导的CAD模型配准方法，可实现复杂零件型面的高精度、高可靠性匹配。

（1）给出了复杂零件检测特征点的选取策略，借助检测特征点来表达零件CAD模型的主要几何特征并确定目标匹配点集，保证测量数据与CAD模型的配准精度，有效提高配准效率。

（2）采用配准可靠性指标筛选所得的目标匹配点集进行配准运算时，可以提高配准可靠性，避免由于零件变形过大导致的模型配准失败。

（3）通过仿真和实际应用试验，验证了本文配准方法的可行性和有效性。

此外，目标匹配点集在优化筛选过程中，随点数递减而不断更新，增加前期处理时间，使整体效率的降低。为此，基于配准可靠性指标的目标匹配点集优化方法有待进一步深入研究，以期达到更好的整体效果。

参 考 文 献

[1]MENQ C H, YAU H T, LAI G Y.Automated precision measurement of surface profile in CAD-directed inspection[J]. IEEE Transactions on Robotics & Automation,1992,8(2):268-278.

[2]王东霞, 温秀兰, 赵艺兵. 基于CAD模型引导测量的自由曲面定位及轮廓度误差评定[J]. 光学精密工程, 2012, 20(12):2720-2727.WANG Dongxia, WEN Xiulan, ZHAO Yibing. Localization and profile error evaluation of freeform surface based on CAD modeldirected measurement[J]. Optics and Precision Engineering, 2012, 20(12):2720-2727.

[3]BESL P J, MCKAY N D. A method for registration of 3D shapes[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 1992,14(2):239-256.

[4]POTTMANN H, LEOPOLDSEDER S,HOFER M. Registration without ICP[J]. Computer Vision & Image Understanding, 2004,95(1):54-71.

[5]LARKINS R L, CREE M J,DORRINGTON A A. Analysis of ICP variants for the registration of partially overlapping timeof-flight range images[C]. Image and Vision Computing New Zealand, Queenstown, 2012.

[6]RUSINKIEWICZ S, LEVOY M. Efficient variants of the ICP algorithm[C]//Proceedings of International Conference on 3-D Digital Imaging and Modeling. Quebec, 2001.

[7]葛宝臻, 彭博, 田庆国. 基于曲率图的三维点云数据配准[J]. 天津大学学报（自然科学与工程技术版）, 2013, 46(2):174-180.GE Baozhen, PENG Bo, TIAN Qingguo.Registration of three-dimensional point-cloud data based on curvature map[J]. Journal of Tianjin University (Science and Technology), 2013,46(2):174-180.

[8]王欣, 张明明, 于晓,等. 应用改进迭代最近点方法的点云数据配准[J]. 光学精密工程, 2012, 20(9):2068-2077.WANG Xin, ZHANG Mingming, YU Xiao,et al. Point cloud registration based on improved iterative closest point method[J]. Optics and Precision Engineering, 2012, 20(9):2068-2077.

[9]敬石开, 程云勇, 张定华,等. 一种区域公差约束的叶片模型配准方法[J]. 计算机集成制造系统, 2010, 16(4):883-886.JING Shikai, CHENG Yunyong, ZHANG Dinghua, et al. Tolerance zone constrained alignment method for turbine blade model[J].Computer Integrated Manufacturing Systems,2010, 16(4):883-886.

[10]谭高山, 张丽艳. 基于最大熵原理的复杂曲面位姿配准技术[J]. 农业机械学报,2014, 45(7):300-305.TAN Gaoshan, ZHANG Liyan. Pose registration technology of complex surfaces based on the maximum-entropyprinciple[J].Transactions of the Chinese Society of Agricultural Machinery, 2014, 45(7):300-305.

[11]SUN Y W, XU J T, GUO D M,et al. A unified localization approach for machining allowance optimization of complex curvedsurfaces[J]. Precision Engineering, 2009,33(4):516-523.

[12]WU H. Research on the localisation of the workpieces with large sculptured surfaces in NC machining[J]. The International Journal of Advanced Manufacturing Technology, 2004,23(5):429-435.

[13]FLACK D. Measurement good practice guide No. 41. CMM Measurement Strategies[M]. NPL, 2001.

[14]CHU Y X, GOU J B, WU H, et al.Localization algorithms: performance evaluation and reliability analysis[C]//Proceedings of IEEE International Conference on Robotics and Automation. IEEE, 1998: 3652-3657.

[15]HORN B K P. Closed-form solution of absolute orientation using unit quaternions[J].Journal of the Optical Society of America A, 1987,4(4):629-642.