知识迁移的极大熵聚类算法及其在纹理图像分割中的应用

程旸，蒋亦樟，钱鹏江，王士同

(江南大学 数字媒体学院，江苏 无锡 214122)

知识迁移的极大熵聚类算法及其在纹理图像分割中的应用

程旸，蒋亦樟，钱鹏江，王士同

(江南大学 数字媒体学院，江苏 无锡 214122)

本文研究了一种新型的基于知识迁移的极大熵聚类技术。拟解决两大挑战性问题: 1)如何从源域中选择合适的知识对目标域进行迁移学习以最终强化目标域的聚类性能；2)若存在源域聚类数与目标域聚类数不一致的情况时，该如何进行迁移聚类。为此提出一种全新的迁移聚类机制，即基于聚类中心的中心匹配迁移机制。进一步将该机制与经典极大熵聚类算法相融合提出了基于知识迁移的极大熵聚类算法(KT-MEC)。实验表明，在不同迁移场景下的纹理图像分割应用中，KT-MEC算法较很多现有聚类算法具有更高的精确度和抗噪性。

迁移学习；中心迁移匹配；极大熵聚类；纹理图像分割；抗噪性

在实际生产中，大部分机器学习方法处理的对象均为含噪数据集且存在数据量不足的问题。如对于图像分割[1]任务而言，图像数据往往含有很大的噪声。图像数据含噪程度越高，使用的机器学习方法对其进行分割的性能就变得越弱。一般来说，无监督的聚类方法通常用来获得图像的分割结果[2-3]，比较著名的算法有模糊C均值算法(FCM)[4]、可能性聚类算法(PCM)[5]、极大熵聚类算法[6]等。这些方法虽简单实用，但其对于含噪图像数据的分割效果并不理想。尽管已有学者致力于解决该问题，但效果并不明显。

1 问题描述

迁移学习技术[7]的提出，为我们提供了一种新的解决问题的思路。传统的机器学习假设训练数据与测试数据服从相同的数据分布。然而，大量实际情况中并不满足这种同分布假设。从另外一个角度上看，如果我们已经有了大量的、在不同分布下的训练数据，完全丢弃这些数据是非常浪费的。如何合理地利用这些数据就是迁移学习要解决的问题。迁移学习可以从现有的数据中迁移知识，用来帮助将来的学习。迁移学习的目标是将从一个环境中学到的知识用来帮助新环境中的学习任务，其学习过程类似人类的学习和思维方式。我们面临的问题如图1所示。

图1 问题描述Fig.1 The description of the problem

源域的数据中往往存在一部分数据为可用数据，如源域优质图像，目标域的数据通常呈现数据不足或噪声污染严重[8-9]等情况，如目标域含噪图像。如何才能得到最接近目标域理想分割的效果图，如果能够将源域的知识成功迁移到目标域中进行学习，是否能够大幅提高图像分割性能呢？

为了验证本文的设想，实现提高图像分割性能的目标，本文将迁移学习方法融入到经典的极大熵聚类算法[10](maximum entropy clustering，MEC)中，以提高极大熵算法的聚类性能，进而提高该算法对图像分割的性能。在将迁移学习策略融入到极大熵聚类算法的过程中，我们面临的挑战有：1)选择源域的何种知识进行迁移学习以增强目标域的聚类性能；2)当源域和目标域的聚类数不一致时如何迁移。

针对挑战1)，本文选用聚类中心作为迁移知识，因源域的聚类中心是各类所包含点的高度浓缩，亦是各类的代表点，将其作为聚类中的高级知识具有更强的指导性；针对挑战2)，本文提出了一个中心迁移匹配机制用于处理源域和目标域聚类数不一致的情况。无论源域与目标域的聚类数是否相同，该中心迁移匹配机制均可适用，且能够找到源域与目标域类中心的最佳匹配关系。将上述迁移知识与中心迁移匹配机制融入到经典的极大熵聚类算法中，本文提出了一种全新的基于知识迁移的极大熵聚类算法，并将该算法成功应用于纹理图像分割中。实验结果表明，本文所提出的基于知识迁移的极大熵聚类算法在不同的迁移场景下对于纹理图像的分割性能均优于其他迁移以及非迁移聚类算法。本文工作的创新主要涵盖以下几点：

1)确定了源域中哪种知识能够进行有效迁移，即从源域数据中获取的聚类中心知识可以用来指导并增强目标域的聚类性能；

2)给出了一种解决源域与目标域聚类数不同时，如何进行有效迁移的途径，即提出了一种通用的中心迁移匹配机制，不仅能够有效解决源域与目标域聚类数不相同时的迁移问题，还能指导源域、目标域聚类数相同时，各类中心如何一一对应的问题。

3)将上述两个问题的解决策略融入到极大熵聚类算法后，本文提出了一种新的基于知识迁移的极大熵聚类算法，实验表明该算法的聚类性能较其他迁移聚类算法以及非迁移聚类算法在处理不同迁移场景下的纹理分割图像时，具有更加优良的性能。

本文所用的符号说明如表1所示。

表1 符号说明

2 相关工作

2.1 经典MEC算法

MEC聚类算法是基于划分的聚类算法中最具代表性的算法之一，该算法的数学表达式简单明了、物理意义明确，是广大学者较常使用的聚类算法，关于MEC算法的变形算法较经典的如文献[10]。特别是在针对含有噪声的纹理图像的分割中，MEC聚类算法相比经典的模糊C均值聚类FCM以及可能性聚类PCM等聚类算法具有更好的抗噪性，进而能够获得更好的聚类性，使得分割结果更加逼近理想分割结果。综上，本文选用了MEC算法。MEC算法的函数表达式为

(1)

式中：xj为第j个数据样本，Vi为第i个聚类中心，uij为样本xj属于聚类中心Vi的隶属度，C为聚类数，N为样本总数，γ为熵的正则化参数， ‖xj-Vi‖2代表样本xj与聚类中心Vi之间的距离。

由拉格朗日乘子法则，求解式(1)，解得聚类中心Vi和隶属度Uij的表达式为

(2)

(3)

MEC算法步骤如下：

1)给定聚类数C，样本总数N，正则化参数γ，聚类精度ε，最大迭代次数T，初始化隶属度矩阵U和聚类中心V；

2)根据式(2)更新聚类中心矩阵V；

3)根据式(3)更新隶属度矩阵U；

5)算法收敛后，输出聚类中心V和隶属度矩阵U。

2.2 相关迁移聚类算法

近年来，迁移聚类算法及其相关算法的研究已受到许多专家学者的关注，本文将研究中较有价值的文献罗列如下：文献[11]提出了一种自学聚类算法，该算法是第1个基于互信息的迁移聚类算法，但是由于该算法运行的前提是假定源域数据是可用的，这在实际生产应用中并不切实际，所以该算法具有一定的局限性；文献[12]提出了一种基于谱聚类的迁移聚类算法，该算法主要针对光谱聚类；文献[13]提出了一种极大熵的迁移聚类算法，该算法提出了基于类中心和隶属度的两种知识迁移机制，但该算法并未解决当源域目标域聚类数不一致时，如何进行迁移的问题。除了直接提出的迁移聚类算法，还存在如协同聚类[14]、多任务聚类[15]、联合聚类[16]、半监督聚类[17]等具有相关性的聚类算法。其中，协同聚类算法的核心思想为结合样本间不同的协作能力形成拉动效应，共同推动事物的发展，从而提高样本的整体聚类精度。多任务聚类的核心思想为多个聚类任务同时进行，各个聚类任务之间相互协调配合，以提高聚类性能。联合聚类顾名思义就是联合多个聚类算法进行一定关系的联合使用，聚类精度的提高对于具体聚类算法的选择比较敏感。半监督聚类算法需要已知一部分数据样本的标签，根据这些标签来指导整个样本数据的聚类过程，从而提高聚类性能。

现有的迁移聚类算法及其相关算法在处理含噪的图像分割数据时，均存在各种问题。如文献[13]提出的迁移聚类算法无法解决当源域与目标域的图像分割数不一致时，如何实现迁移的问题。对于其他相关算法如联合算法来说，图像本身还有噪声，经过层层的聚类算法进行处理，误差被层层放大，最终的聚类性能则被削弱。本文所做研究主要针对纹理图像分割进行展开，我们将在下一节针对算法的抗噪性、源域目标域聚类数是否一致等问题进行详细描述。

3 基于知识迁移的MEC聚类算法

3.1 基于聚类中心的知识迁移机制

源域中存在许多知识可用于迁移到目标域中进行学习。问题在于在具体选择时，应该选择哪种或哪几种知识的组合进行迁移。源域中存在可以迁移的知识主要有：聚类中心、隶属度、数据样本以及其他经过二次或多次处理后获得的知识。考虑到源域的聚类中心具有较高的数据集中特征，且该知识作为自然聚类知识的核心，本文最终选择了聚类中心作为知识迁移的对象。基于中心迁移的表达式计算的是源域的聚类中心Vs与目标域Vt之间距离和。

(4)

式中：λ为迁移平衡参数，一般大于0，其值越大，表示源域知识在目标域中所占分量越大；Ct为目标域聚类数；Vj,t为目标域中第j个聚类中心；Vj,s为源域中第j个聚类中心。

3.2 基于聚类中心的迁移匹配机制

式(4)尽管实现了源域知识向目标域迁移进行指导学习的目的，但其并未解决源域与目标域的聚类数不相同时，如何进行迁移和中心间的匹配问题。本小节，我们将致力于探讨能否确定一个通用的准则，无论源域与目标域的聚类数是否一致均能自适应地匹配。为了解决上述问题，本文引入了模糊聚类理论来解决该问题，从而提出了一种中心迁移匹配机制。中心迁移匹配机制的表达式为

(5)

式(5)解决了源域的聚类中心Vs与目标域Vt之间的匹配问题。其中，参数Pt,s为知识迁移隶属度，pjk表示目标域的第j个类中心与源域的第k个类中心进行匹配的隶属度。当pjk→1，表示目标域的第j个类中心完全匹配源域的第k个类中心；当pjk→0，表示目标域的第j个类中心不匹配源域的第k个类中心，若出现不匹配的情况，源域中未找到匹配聚类中心的那个聚类中心将会从源域的聚类中心中删除掉。Nt为目标域数据样本的大小，Ct为目标域聚类数，Cs为源域聚类数。

3.3 基于知识迁移的极大熵聚类算法

将上述知识迁移机制与知识匹配机制融入到MEC聚类算法后，本文提出一种基于知识迁移的极大熵聚类算法。该算法的流程主要分为两个阶段，流程图如图2所示。

图2 KT-MEC算法流程图Fig.2 The flowchart of KT-MEC algorithm

1)知识提取

利用经典的极大熵聚类算法对源域的数据集进行聚类，得到源域的聚类中心Vs。知识提取的表达式为

(6)

通过求解式(6)，得到源域聚类中心Vs。

2)知识匹配与迁移

利用中心迁移匹配机制将阶段1得到的聚类知识进行自适应匹配，使源域中的聚类中心(知识)能够与目标域中的聚类中心进行完美匹配，以解决源域和目标域不同类时的迁移问题。同时，将匹配后的源域知识迁移到目标域中加以利用。结合极大熵聚类算法，基于知识迁移的极大熵聚类算法(KT-MEC)，该算法的函数表达式为

(7)

1≤j≤Nt,1≤i≤Ct,1≤k≤Cs

式中：uij,t为目标域隶属度，xj,t为目标域第j个样本数据，Vi,t为目标域第i个聚类中心，γ为熵的正则化参数，Ct为目标域聚类数，Nt为目标域样本总数，λ为知识迁移的平衡系数，pik表示目标域的第i个类中心迁移到源域的第k个类中心的知识迁移隶属度，Vk,s为源域的第k个类中心，η为迁移项的正则化参数。通过拉格朗日乘子法最小化式(7)，各参数表达式如下：

目标域隶属度uij,t：

目标域聚类中心vi,t：

知识迁移隶属度pik：

通过上述两个阶段的流程，将各源域与目标域的相关数据带入到各表达式中，得到最终的聚类结果。KT-MEC聚类算法的详细步骤如下：

输入 源域数据集xs，目标域数据集xt，源域聚类数Cs，目标域聚类数Ct，熵的正则化参数γ，收敛精度ε，最大迭代次数T；

输出 目标域隶属度Ut，目标域聚类中心Vt。

知识提取阶段:

1)随机初始化源域的隶属度矩阵Us；

2)利用式(2)求得源域的聚类中心Vs；

3)利用式(3)求得源域的隶属度Us；

4)满足迭代终止条件则输出源域聚类中心Vs并终止算法，否则返回 2)。

知识匹配与迁移阶段:

1)随机初始化目标域的隶属度矩阵Ut以及聚类中心Vt；

2)利用式(8)求得目标域的隶属度矩阵Ut；

3)利用式(9)求得目标域聚类中心矩阵Vt；

4)利用式(10)求得目标域的知识迁移隶属度矩阵Pts；

5)如满足迭代终止条件则输出目标域隶属度矩阵Ut，聚类中心Vt，并终止算法，否则返回2)。

4 实验与分析

为了评估本文所提KT-MEC聚类算法的性能，实验所使用的对比算法有：非迁移MEC聚类算法、自学聚类算法(STC)[11]、迁移谱聚类算法(TSC)[12]、DRCC协同聚类算法[15]、CombKM多任务聚类算法[15]。本文实验所用数据集为Brodatz纹理图像分割[17]数据集。

Brodatz纹理图像由7个基本纹理图像(D3、D6、D21、D49、D53、D56、D93)合成，具体见图3。合成纹理图像的大小被重新调整为100像素×100像素。为了模拟真实数据集环境，本文将不同标准偏差的高斯噪声添加到各个纹理图像中。实验中，图3(a)为源域的图像数据，图3(b)～(i)为在不同的目标域中的图像数据。为了模拟不同的迁移场景，我们设计了两种不同迁纹理图像分割任务，目标域图像T1～T4与源域图像的类别数均为7，σ=0.1,0.2,0.0,0.1；目标域图像T5～T8与源域图像的类别数分别为3、4、5、6，σ=0.1。

图3 源域及不同情况下目标域的纹理图像数据Fig.3 Texture image datasets of one source domain and some different target domains

理想分割图可用来为各算法的分割性能优劣作参考，理想的纹理分割结果如图4所示。

图4 不同纹理图像的理想分割结果Fig.4 Ideal segmentation result of different texture images

纹理图像分割的过程概括如下。文献[19]先采用Gabor滤波器在6个方向提取纹理图像特征的滤波器组。每个纹理图像的数据集包含30维特征，数据集大小为10 000。不同算法得到的类被认为分割图像的一个区域。

4.1 实验参数设置

通常用来衡量聚类算法性能的指标有：NMI、RI、Entropy、F-measure等，本文主要采用以下两种评估指标：

式中：Ni,j表示第i个聚类与类j的契合程度，Ni表示第i个聚类所包含的数据样本量，Nj表示类j所包含的数据样本量，而N表示整个数据样本的总量大小。RI表达式中的f00表示数据点具有不同的类标签并且属于不同类的配对点数目，f11则表示数据点具有相同的类标签并且属于同一类的配对点数目，而N表示整个数据样本的总量大小。NMI、RI两种评价指标的取值范围均为[0,1]，取值越大表明算法的性能越好。

在本文所使用的迁移算法中，KT-MEC算法的熵正则化参数γ∈{0∶0.05∶1}，迁移平衡因子λ∈{0.1,0.5,1,5,10,50,100,500,1 000}，迁移隶属度的正则化参数η∈{0∶0.05∶1}。TSC算法和STC算法的参数设置详见文献[11]和文献[12]。

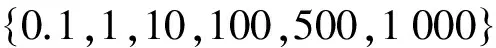
上述所有参数均由网格搜索[18]得到最优值，实验结果均为运行算法15次的结果取均值及方差所得。实验均在MARTLAB8.1.0.604(R2013a)平台下完成，操作系统为64位Windows7，CPU为Intel(R)Core(TM)i3-3240 3.40GHz，内存为4GB。

4.2 聚类数相同的纹理图像分割

表2与图5分别为源域与目标域聚类数相同时，各算法对纹理图像进行分割时的聚类性能对比与图像分割结果对比。

表2 源域与目标域的聚类数相同时的各算法聚类性能对比

(a) 6种算法分别在数据集T1上的图像分割结果

(b) 6种算法分别在数据集T2上的图像分割结果

(c) 6种算法分别在数据集T3上的图像分割结果

(d) 6种算法分别在数据集T4上的图像分割结果 图5 源域与目标域聚类数相同的含噪纹理图像分割结果Fig.5 Segmentation results of clustering algorithms for noisy texture images with the same number of clusters between source domain and target domain

从表2和图5的聚类结果可以观察到，迁移聚类算法(STC、TSC、KT-MEC)在T1～T4数据集上取得了比传统的非迁移聚类算法更高的聚类精度。表2中NMI和RI值以及图5中可视化的分割结果，均表明本文所提出的KT-MEC聚类算法优于经典的MEC算法。以上结果进一步表明，在含噪的数据环境中，本文KT-MEC算法具有比MEC更好的鲁棒性，也进一步表明迁移学习技术是提高算法鲁棒性的有效途径。

如表2和图5的聚类结果所示，本文提出的KT-MEC算法与协同算法DRCC以及多任务聚类算法CombKM相比，本文算法仍然较优，这是因为多任务聚类与迁移聚类的原理明显不同。协同聚类与多任务聚类在集中完成多个聚类任务的同时，通过使用每个聚类任务的独立信息和多个聚类任务间的潜在相关信息，以获得良好的聚类性能。然而，在迁移聚类场景中，目标域的数据不能提供正确的聚类信息，这就会使得协同聚类和多任务聚类算法的聚类性能变弱。

此外，由于本文提出的KT-MEC算法较其他迁移聚类算法、协同聚类算法、多任务聚类算法具有更好的聚类性能，这进一步表明先进的集群知识(如聚类中心)可以被看作是一种有效的迁移知识，以提高目标域的聚类性能。这也表明本文提出的聚类中心自适应匹配机制能使源域的类中心与目标域的类中心进行成功匹配，达到知识迁移的目的。

4.3 聚类数不同的纹理图像分割

表3与图6分别为源域与目标域聚类数不同时，各算法对纹理图像进行分割时的聚类性能对比与图像分割结果对比。

由于协同聚类算法DRCC、迁移聚类算法STC和TSC的聚类机制需要源域与目标域有相同的聚类数，所以这3种聚类算法不能在源域与目标域聚类数不同的迁移场景下运行。

表3和图6的实验结果表明本文提出KT-MEC聚类算法在图像分割性能上较经典的非迁移MEC算法以及CombKM算法具有更优的聚类性能。此外，得益于本文提出的基于知识的中心迁移机制，源域与目标域聚类数不同的迁移场景中的聚类结果表明了本文提出的基于知识的中心匹配机制可挖掘出源域和目标域之间完美的聚类中心的配对关系，进而确保知识迁移的质量。

表3 源域与目标域的聚类数不同时的各算法聚类性能对比

续表3

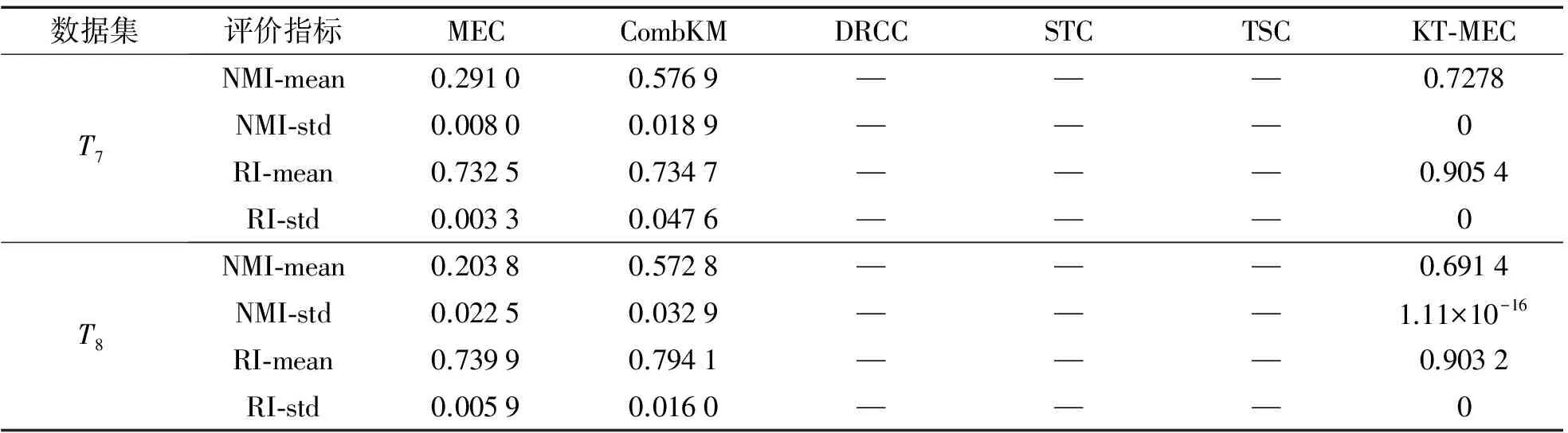
数据集评价指标MECCombKMDRCCSTCTSCKT⁃MECT7NMI⁃mean0．29100．5769———0．7278NMI⁃std0．00800．0189———0RI⁃mean0．73250．7347———0．9054RI⁃std0．00330．0476———0T8NMI⁃mean0．20380．5728———0．6914NMI⁃std0．02250．0329———1．11×10-16RI⁃mean0．73990．7941———0．9032RI⁃std0．00590．0160———0

(a) 6种算法分别在数据集T5上的图像分割结果

(b) 6种算法分别在数据集T6上的图像分割结果

(c) 6种算法分别在数据集T7上的图像分割结果

(d) 6种算法分别在数据集T8上的图像分割结果 图6 源域与目标域聚类数不同的含噪纹理图像分割结果Fig.6 Segmentation results of clustering algorithms for noisy texture images with the different number of clusters between source domain and target domain

上述实验结果表明本文提出的KT-MEC聚类算法在不同的迁移场景中的聚类性能均优于现有的相关聚类算法。特别是，KT-MEC聚类算法适用于一般的迁移场景，即无论是源域和目标域的聚类的数目是相同或不同时，本文KT-MEC算法均能适用且能获得比其他聚类算法更好的聚类结果。

5 结束语

本文研究是基于迁移学习的聚类算法，实验部分主要针对纹理图像的分割。本文算法对迁移聚类算法的贡献主要有两方面：1)确定了聚类中心作为迁移知识，实验证明了将聚类中心作为迁移知识能够更好地增强目标域的聚类性能；2)找到了一个解决无论源域与目标域的聚类数是否一致，都能够成功进行迁移的通用策略。基于上述工作，结合传统的非迁移极大熵聚类算法，本文提出了基于知识迁移的极大熵聚类算法，并将该算法与其他迁移算法、非迁移算法、协同聚类算法、多任务聚类算法等一系列相关算法进行了性能对比，实验表明本文KT-MEC聚类算法的性能在纹理图像分割上较其他算法具有更加优良的性能。KT-MEC聚类算法不仅能够提高算法的聚类精度，增强图像的分割效果，还能适应不同迁移场景下的聚类任务，具有较强的鲁棒性。

虽然本文KT-MEC聚类算法在纹理图像的分割上具有较好的性能，但该算法的适应性上还需进行进一步的研究。随着数据的爆炸式增长，数据复杂性的迅速增加，KT-MEC聚类算法是否能够适用于高维复杂数据还有待研究。

[1]ZHU Lin, CHUNG F L, WANG Shitong. Generalized fuzzy c-means clustering algorithm with improved fuzzy partitions[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2009, 39(3): 578-591.

[2]KIM S, YOO C D, NOWOZIN S, et al. Image segmentation usinghigher-order correlation clustering[J]. IEEE transactions on pattern analysis and machine intelligence, 2014, 36(9): 1761-1774.

[3]JIANG Yizhang, CHUNG F L, WANG Shitong, et al. Collaborative fuzzy clustering from multiple weighted views[J]. IEEE transactions on cybernetics, 2015, 45(4): 688-701.

[4]BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. USA: Springer Science & Business Media, 2013: 155-201.

[5]KRISHNAPURAM R, KELLER J M. A possibilistic approach to clustering[J]. IEEE transactions on fuzzy systems, 1993, 1(2): 98-110.

[6]KARAYIANNIS N B. MECA: maximum entropy clustering algorithm[C]//Proceedings of the Third IEEE Fuzzy Systems Conference. Orlando, USA: IEEE, 1994: 630-635.

[7]PAN S J, YANG Qiang. A survey on transfer learning[J]. IEEE transactions on knowledge and data engineering, 2010, 22(10): 1345-1359.

[8]DENG Zhaohong, CHOI K S, JIANG Yizhang, et al. Generalized hidden-mapping ridge regression, knowledge-leveraged inductive transfer learning for neural networks, fuzzy systems and kernel methods[J]. IEEE transactions on cybernetics, 2014, 44(12): 2585-2599.

[9]DENG Zhaohong, JIANG Yizhang, CHOI K S, et al. Knowledge-leverage-based TSK fuzzy system modeling[J]. IEEE transactions on neural networks and learning systems, 2013, 24(8): 1200-1212.

[10]ZHI Xiaobin, FAN Jiulun, ZHAO Feng. Fuzzy linear discriminant analysis-guided maximum entropy fuzzy clustering algorithm[J]. Pattern recognition, 2013, 46(6): 1604-1615.

[11]DAI Wenyuan, YANG Qiang, XUE Guirong, et al. Self-taught clustering[C]//Proceedings of the 25th International Conference on Machine Learning. New York, USA: ACM, 2008: 200-207.

[12]JIANG Wenhao, CHUNG F L. Transfer spectral clustering[M]//FLACH P A, DE BIE T, CRISTIANINI N. Machine Learning and Knowledge Discovery in Databases. Berlin Heidelberg: Springer, 2012: 789-803.

[13]钱鹏江, 孙寿伟, 蒋亦樟, 等. 知识迁移极大熵聚类算法[J]. 控制与决策, 2015, 30(6): 1000-1006. QIAN Pengjiang, SUN Shouwei, JIANG Yizhang, et al. Knowledge transfer based maximum entropy clustering[J]. Control and decision, 2015, 30(6): 1000-1006.

[14]PEDRYCZ W, RAI P. Collaborative clustering with the use of Fuzzy C-Means and its quantification[J]. Fuzzy sets and systems, 2008, 159(18): 2399-2427.

[15]GU Quanquan, ZHOU Jie. Learning the shared subspace for multi-task clustering and transductive transfer classification[C]//Proceedings of the Ninth IEEE International Conference on Data Mining. Miami, USA: IEEE, 2009: 159-168.

[16]GU Quanquan, ZHOU Jie. Co-clustering on manifolds[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York, USA: ACM, 2009: 359-368.

[17] RANDEN T. Brodatz texture[EB/OL]. [2015-12-14]. http://www.ux.uis.no/～tranden/brodatz.html.

[18]DENG Zhaohong, CHOI K S, CHUNG F L, et al. Enhanced soft subspace clustering integrating within-cluster and between-cluster information[J]. Pattern recognition, 2010, 43(3): 767-781.

[19]KYRKI V, KAMARAINEN J K, KLVIINEN H. Simple Gabor feature space for invariant object recognition[J]. Pattern recognition letters, 2004, 25(3): 311-318.

程旸，男，1991年生，硕士研究生，主要研究方向为人工智能、模式识别、数据挖掘。

蒋亦樟，男，1988年生，博士，讲师，主要研究方向为人工智能、模式识别、模糊系统。

钱鹏江，男，1979年生，副教授，博士，主要研究方向为模式识别、医学图像处理、大数据。

A maximum entropy clustering algorithm based onknowledge transfer and its application to texture image segmentation

CHENG Yang， JIANG Yizhang， QIAN Pengjiang， WANG Shitong

(School of Digital Media, Jiangnan University, Wuxi 214122, China)

In this paper, we propose a novel technique for maximum entropy clustering (MEC) based on knowledge transfer. More specifically, we aim to solve the following two challenging questions. First, how can knowledge be appropriately selected from a source domain to enhance clustering performance in the target domain via transfer learning? Second, how best do we conduct transfer clustering if the number of clusters in the source domain and the target domain are inconsistent? To address these questions, we designed a new transfer clustering mechanism called the central matching transfer mechanism, which we based on clustering centers. Further, we developed a knowledge-transfer-based maximum entropy clustering (KT-MEC) algorithm by incorporating our mechanism into the classic MEC approach. Our experimental results reveal that our proposed KT-MEC algorithm achieves a higher level of accuracy and better noise immunity than many existing methods when applied to texture image segmentation in different transfer scenarios.

transfer learning; center transfer matching; maximum entropy clustering; texture image segmentation; robustness

2016-03-04.

日期：2016-08-24.

国家自然科学基金项目(61572236);江苏省自然科学基金项目(BK20160187);江苏省产学研前瞻性联合研究项目(BY2013015-02).

蒋亦樟. E-mail：jyz0512@163.com.

10.11992/tis.201603005

http://www.cnki.net/kcms/detail/23.1538.tp.20160824.0928.004.html

TP181

A

1673-4785(2017)02-0179-09

程旸，蒋亦樟，钱鹏江，等. 知识迁移的极大熵聚类算法及其在纹理图像分割中的应用[J]. 智能系统学报， 2017, 12(2): 179-187.

英文引用格式：CHENG Yang， JIANG Yizhang， QIAN Pengjiang， et al. A maximum entropy clustering algorithm based on knowledge transfer and its application to texture image segmentation[J]. CAAI transactions on intelligent systems, 2017, 12(2): 178-187.