一种用于电力变压器故障识别的理论方法研究

杨 梅

1 引言

在冶金行业中，变压器作为电气设备的枢纽，其运行情况直接影响整个电力系统的安全。对变压器进行故障检测，对于提高电力系统的可靠性有着重要意义。对变压器故障进行识别，及时发现变压器内部故障的性质和未来发展趋势，准确掌握变压器的运行状况，也是制定变压器维护措施和检修计划的重要依据。目前广泛使用的气体色谱分析法是检测变压器内部故障性质的重要方法［1］。

支持向量机是一种以小样本统计学习理论为基础发展起来的新型通用学习方法，有效地解决了小样本、高维数、非线性等的学习问题，并克服了人工神经网络学习难以确定合理结构和存在局部最优的缺点，大大地提高了学习方法的泛化能力。目前支持向量机已经广泛应用于手写字体识别［2］、人脸识别［3］、遥感图像分类［4］等领域，并取得了良好的效果。本文将支持向量机引入变压器故障诊断中，提出了基于多分类支持向量机的变压器故障诊断方法，对变压器故障进行分类，以达到设备状态监测的目的。

2 最小二乘支持向量机

支持向量机方法在处理非线性问题时，将输入空间通过特定的函数进行非线性映射，将原输入空间变换到高维特征空间；然后，在高维空间中根据结构风险最小化原则寻找最大间隔最优线性分类超平面。此超平面对应着原输入空间的非线性分类面，分类后将高维空间的最优线性分类超平面做逆映射，从而得到原输入空间的非线性分类面。支持向量分类器只涉及到向量间（原输入空间或变换后的空间）的内积运算，因此，可以很好地应用核函数的方法来解决高维空间中的维数灾难问题，减少计算量。

最小二乘支持向量机（Least Squares Support Vector Machine，LS-SVM）则是在标准支持向量机的一种扩展。它采用最小二乘线性系统误差平方和作为损失函数［5］，将求解过程变成了解一组等式方程，提高了求解速度，减少了计算资源。在原始空间的最小二乘支持向量机分类问题描述为：

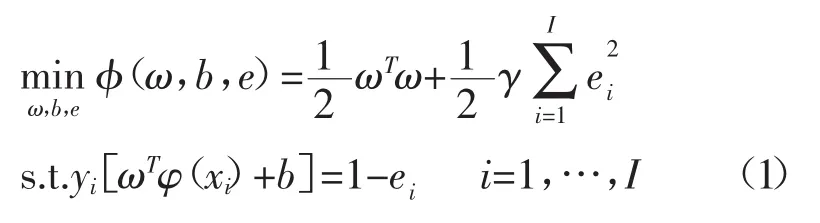
定义拉格朗日函数：

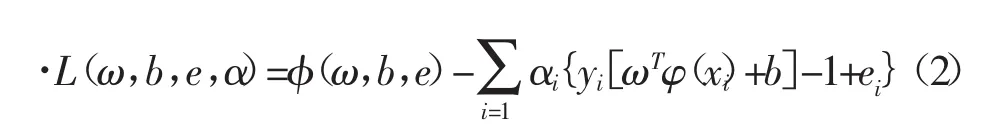
其中，αi∈R，根据优化条件

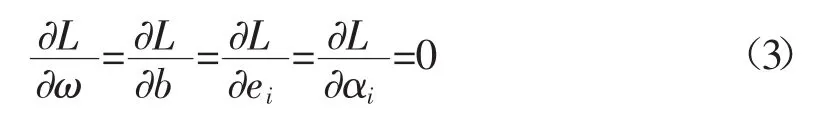
消除ω和ε后，得到矩阵方程：

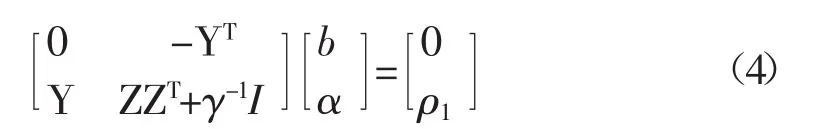
定义 Ω＝ZZT＝［qij］l×l，根据 Mercer［6］条件，该矩阵的元素可以表示为：

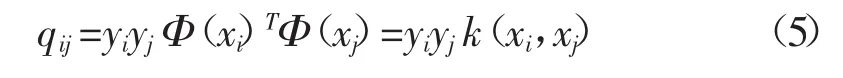
求解上述问题后可得到最优分类函数如下：

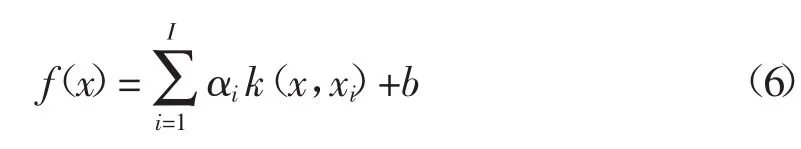
假定高维特征空间的内积函数为：

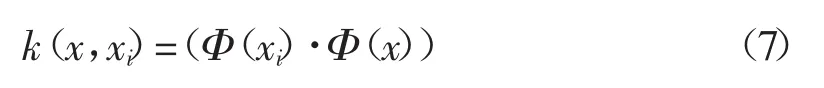
称上式的内积函数为核函数。只要一种核函数k（xi，xj）满足Mercer条件它就对应某一变换空间中的内积。

本文选用高斯径向基函数，如式（8）所示：

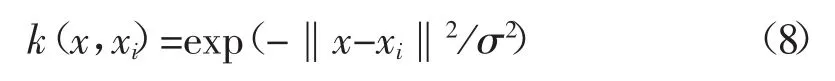
其中，σ≠0为方差。由此可知，待优化的变量包括核参数σ和正则化参数γ。

3 基于多分类支持向量机的电力变压器故障识别

电力变压器故障识别对象最常见的有4种状态：电力变压器的高能放电、低能放电、过热和正常状态。基于多分类支持向量机的电力变压器故障识别过程，包括变压器故障状态的特征提取、训练和测试。

3.1 适应度函数的选取

变压器故障诊断是个多分类问题，而支持向量机适用于二分类问题，因此，采用支持向量机解决变压器故障诊断问题时，就需要将多分类问题转化为二分类问题。

通常通过构造多个二分类器，将一个多分类问题转化为多个二分类问题。处理多分类问题时，最小输出编码相对于其他编码方式所需计算时间最短［7］。因此，本文采用最小输出编码方式解决多分类问题。

已知多分类问题的样本类别数为C。当采用最小输出编码方式解决多分类问题时，对于C类问题需要的二分类器数为能表示C的最小二进制数的位数。在支持向量机的参数优化问题中，为减少计算量，不需要对每个子二分类支持向量机的超参数都进行选择，而是通过最小输出编码方法的编码和解码过程把个二分类机作为一个整体，形成一个多分类支持向量机。

由上可知，支持向量机需要选择的超参数为σ和γ，根据仿真优化问题模型，直接利用支持向量机分类后的结果，通过计算分类正确率来表示个体的适应度，具体表示如下：

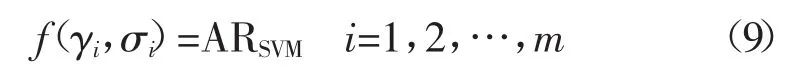
其中，m为遗传算法中的种群规模，本文中3.2章节有详细介绍。

通过独立输出编码方法得到的多分类支持向量机模型的性能采用正确率（theAccuracyRate，AR）作为评价指标，记为：

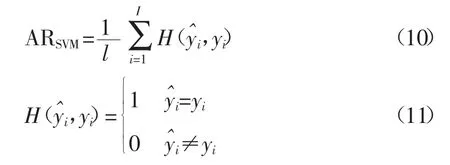
其中，yi为实际值，为模型预测输出，l为样本数。表示分类结果，分类正确为1，反之为0。

3.2 遗传算法的进化操作

遗传算法［8］（GeneticAlgorithms，GA）是基于生物界的自然选择和自然遗传机制的基本思想形成的一类优化方法。由于它采用群体搜索和基于交叉算子、变异算子实现群体中个体之间的信息交换，使其具有隐含并行性，大大提高了搜索的效率，同时克服了传统优化方法对于目标函数有连续、可微的要求。因此，遗传算法在实际问题中得到了广泛应用。

遗传算法中，描述和评价待优化问题中的每个解，以及实现选择、交叉、变异等进化操作是算法的核心问题。

3.2.1 个体编码

遗传算法中，搜索空间中的每个解都是通过以一定编码方式表示的个体加以描述的。因此，合理的编码方式是保证后续进化操作的基础。目前，常用的编码方式有二进制编码、实数编码等。本章中，支持向量分类模型中的超参数通常为实数，因此，采用实数编码方式描述待优化参数σ和γ，记个体为 x＝（γ，σ）。

3.2.2 选择算子

选择算子根据种群中个体的适应度，按照一定的规则，从第t代种群中选择出较优势个体遗传到下一代种群。目前，常用的选择算子有轮盘赌选择、联赛选择、精英保留选择等选择方法。本章中，为保证每代的最优个体进入下一代种群，采用随机联赛选择和最优个体保留方法相结合的方法选择算子，具体操作如下。

第一步：从当前种群中选出具有最高适应度值的个体和具有最低适应度值的个体。如果当前种群中最优个体适应度大于保留集中的最优个体适应度，则将当前种群中的最优个体保存在保留集中，作为新的保留集最优个体；同时，用保留集最优个体替代当前种群中的最差个体。

第二步：从种群中随机选取N（N＝2）个个体，比较其适应度大小；并将具有较大适应度的个体遗传到下一代种群中。

第三步：将上述过程重复m次，得到下一代种群的m个个体。这里，m为种群规模。

3.2.3 交叉算子

交叉算子是将种群中随机配对的个体，以某一概率对二者进行基因重组。针对不同编码方式的个体，有多种不同的交叉算子。目前，常用的交叉算子包括实数编码的算数交叉，二进制编码的单点交叉、多点交叉等。本章中，鉴于个体采用实数编码方式，所以采用算术交叉。

算术交叉就是将两个个体通过线性组合，生成两个新个体。针对个体xa（t）和xb（t），以交叉概率Pc运用算术交叉后产生的新个体是：

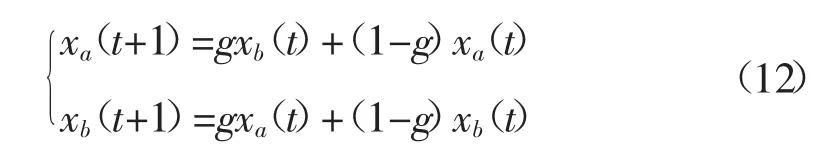
其中，g为［0，1］之间的常数。

3.2.4 变异算子

变异操作就是对种群中的某些个体，以某一概率改变其某一个或某一些基因位上的取值。该操作对于提高算法的搜索能力具有重要作用。针对不同编码方式的个体，有多种不同的变异算子。目前，常用的变异算子包括实数编码的非均匀变异，二进制编码的单点变异、多点变异等。本章中，考虑到个体采用实数编码方式，所以采用非均匀变异算子。

非均匀变异算子就是以变异概率Pm随机对个体中某一变量值进行非均匀变异。例如：假设变异前后的个体分别为。若发生变异的变量 γ 的取值范围为［γmin，γmax］，那么非均匀变异操作记为：

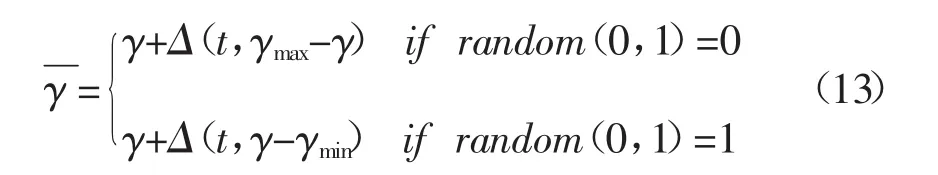
其中，△（t，e）（e 代表 γmax-γ 或 γ-γmin）表示［0，e］范围内符合非均匀分布的一个随机数。

3.3 数据预处理和特征提取

本文分析的基础是利用色谱分析得到的各种特征气体（包括 H2、CH4、C2H6、C2H4和 C2H2等）含量信息，它反映了电力变压器的高能放电、低能放电、过热和正常4种状态的特征信息，这些数据都是绝对值数据，每个测试数据都是由反映这些特征气体含量的n+1个分量［9］组成（n由实际情况决定）。为方便进行训练和识别，需要对检测出的特征气体含量进行预处理，以得到变压器故障识别需要的各种特征量，组成的训练样本具体如下。

（1）n种特征气体的相对含量：

其中，cn为第n种特征气体的绝对含量。

（2）反映各组测试数据之间横向比较信息的一个特征量，它通过下式得到：

这样就得到了n+1个特征量，组成一个n+1维的特征向量 X＝［x1x2x3…xnxn+1］T，该特征向量反映了识别高能放电、低能放电、过热和正常4种变压器状态需要的各种特征信息。

将特征向量作为多分类支持向量机的输入对模型进行训练，4类问题需要的二分类器数为2个。根据实际情况，将训练好的支持向量机用于测试。

4 结束语

本文将遗传算法与支持向量机结合，提出了一种基于遗传算法的支持向量分类超参数选择方法。进一步将遗传算法优化得到的参数应用到多分类支持向量机模型中，针对电力变压器故障识别问题，利用气体色谱分析法采集数据，并对采集的数值进行预处理得到特征值，对多分类支持向量机进行训练和识别，判断输出变压器所处的状态，预测设备的未来发展趋势，降低故障发生率。

参考文献：

［1］孙才新，郭俊峰，郑海平等.基于行为的变压器油色谱分析模糊诊断专家系统研究.电工技术学报，2001，16（3）：49-53.

［2］张 凯，王建平.基于混合核函数的脱机手写汉字识别.计算机与数字工程，2007（12）：25-27.

［3］.贾云得.机器视觉.科学出版社，2000.

［4］Yi-nan Guo， Mei Yang，Da-wei Xiao.The Selection Method for Hyper-parameters of Support Vector Classification by Chaotic Cultural Algorithm.International Journal of Intelligent Computing and Cybernetics，2010，3（3）：449-462.

［5］邓乃扬，田英杰.数据挖掘中的新方法：支持向量机.北京：科学出版社，2004.

［6］方瑞明.支持向量机理论及其应用分析.北京：中国电力出版社，2007.

［7］陈小娟.支持向量机及其在多属性决策中的应用.西安电子科技大学，2008.

［8］Yi-nan Guo，Da-wei Xiao，Mei Yang.Genetic Algorithm-Based Support Vector Classification Method for Multispectral Remote Sensing Image，Lecture Notes in Computer Science.2010.6328：213-221.

［9］吕干云，程浩忠，董立新，等.基于多级支持向量机分类器的电力变压器故障识［J］.电力系统及其自动化学报，2005，17（1）：19-22.