无功功率与电抗性元件储能之间关系的研究
2017-05-15汪圣杰詹金华胡国华
汪圣杰,詹金华,胡国华
(1.合肥学院 电子信息与电气工程系,合肥 230601;2.合肥市公安局 警令部,合肥 230041)
无功功率与电抗性元件储能之间关系的研究
汪圣杰1,詹金华2,胡国华1
(1.合肥学院 电子信息与电气工程系,合肥 230601;2.合肥市公安局 警令部,合肥 230041)
正弦交流电路有两种不同类型的功率:有功功率(P)、无功功率(Q)。通过讨论这两种功率的特点并定性地给出了关于这两种功率的结论,随后针对无功功率的独特特性,给出了电抗性元件(电感以及电容)的无功功率的理论定义式,然后在理论上推导了电抗性元件无功功率理论定义式与电抗性元件储能之间的关系。推导的过程表明在正弦交流电路中,无功功率(Q)有区别于有功功率(P)的独特特性即无功功率不是瞬时功率的平均效果值,可以利用无功功率进行积分从而得到电抗性元件的储能。
交流电路;有功功率;无功功率;电抗性元件的储能
0 引 言
在正弦激励的交流电路中,[1-2]由于电路的激励源是正弦电压源或是正弦电流源,根据电路原理中的理论,正弦变化的电压源或电流源在电路中产生的响应也将是同频的正弦电压或是同频的正弦电流。由于正弦的电压和电流其幅度是随着时间而变化的,因此在负载上的响应即正弦的电压和电流所产生的功率也将是一个随时间而变化的量,这个随时间变化的功率称为瞬时功率并且用符号p(t)表示,即p(t)=vi(watts),图1给出了一个交流电路中典型的三个量,即正弦电压的波形、正弦电流的波形以及二者所产生的典型的功率波形。
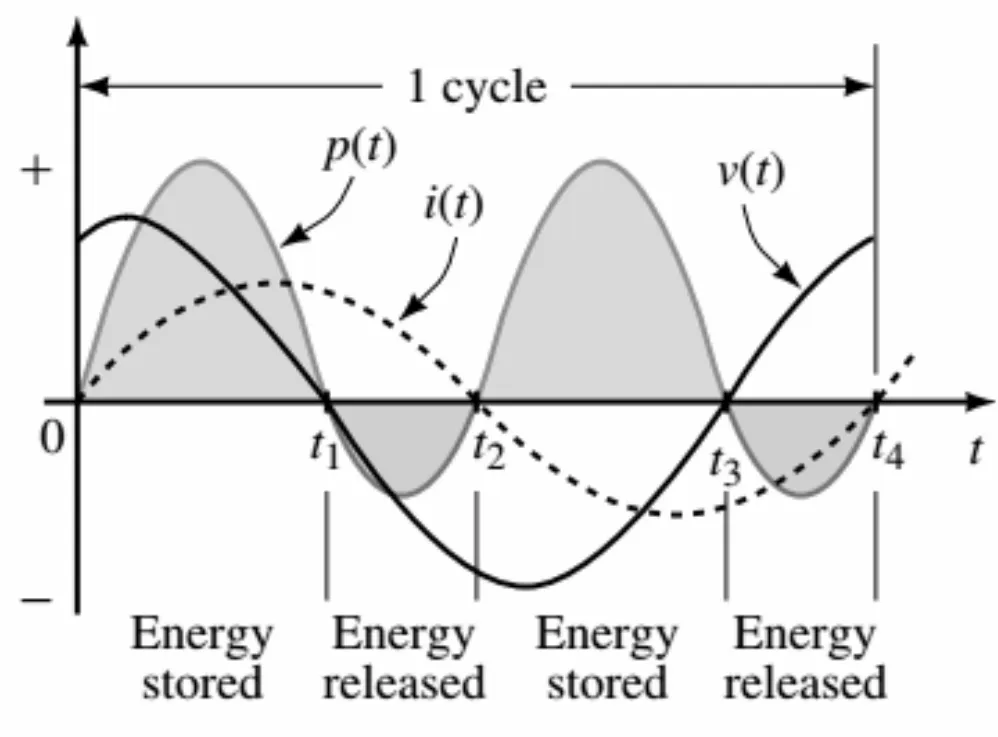
图1 交流电路中的典型功率波形
从图1中可以看出,瞬时功率波形是一种随时间变化的波形,这与直流电路中的功率波形不一样,在直流电路中,功率波形不随时间变化,反映在图形上就是功率波形是一条平行于时间轴的直线。从图1的瞬时功率波形可以得到正弦交流电路中的两种重要的不同类型的功率:[3-4]
①有功功率(P)。从图1中的瞬时功率曲线p(t),可以通过类似于求平均值的方法计算出该瞬时功率在周期内平均效果,即通过数学积分方法求出瞬时功率在一个周期内的平均值,这个平均值即为有功功率,也称为平均功率、实功率。因此如果需要计算正弦交流电路中负载实际消耗的能量,则只需要将有功功率乘以时间间隔就能得到负载实际所消耗的能量(W=Pt)。
②无功功率(Q)。从图1中也可以看到,瞬时功率p(t)在一个周期内也存在负值,p(t)为负值的时间里,功率方向实际是从负载返回的,当然功率的返回只有当负载含有电抗性元件:L或C才发生。功率中流入负载并又从负载返回来的那一部分称的功率之为无功功率。[5]从以上无功功率的定义中可以看出无功功率与有功功率定义是不同的,有功功率是瞬时功率在一个周期内的平均值,而无功功率是流入负载又被负载返回的功率,这并没有说无功功率是平均值,因为没有对p为负值的部分求平均值,因此如果需要计算电抗性元件储存的能量是不能使用诸如W=Qt这样的公式,下面就来研究电抗性元件的无功功率定义以及如何通过无功功率来得出电抗性元件的储能,即无功功率与电抗性元件储能之间的关系。
1 无功功率的定义
1.1 电感的无功功率定义

图2 纯电感性负载电路
对于一个纯电感性负载电路,如图2所示。

(1)

1.2 电容的无功功率定义

图3 纯电容性负载电路
对于一个纯电容性负载电路,如图3所示。

(2)

2 无功功率与电感或电容储能之间的关系

(3)
2.1 电感储存的能量
(4)

(5)

(6)
由公式(6)看出,可以通过无功功率得到了电感所储存的能量。
2.2 电容储存的能量
(7)
考察电感瞬时功率波形可知。电容中储存的能量可以通过对功率从T/4到T/2求积分,对应的电压上下限为0到V,即有:
(8)

由公式(2)可知,输送给容性负载的瞬时功率为pC=-VIsin2ωt=-QCsin2ωt,那么对这个瞬时功率在合理时间段内积分,就可以得到电容所储存的能量。由于能量在T/4到T/2时间内流入电感,因此电容储存的能量可以做如下的积分:
(9)
由公式(9)可以看出,同样也可以通过无功功率得到了电容所储存的能量。
3 结 论
本文阐明了正弦交流电路中的电抗性元件的无功功率与电抗性元件储存的能量之间的关系,通过研究发现电抗性元件的无功功率不是平均值,它是一个定义值,通过无功功率确定电抗性元件储存的能量与通过有功功率确定实际消耗能量这两者有本质的区别,即不能通过简单地将无功功率乘以时间间隔来确定电抗性元件储存的能量。但是可以通过无功功率来确定电抗性元件储存的能量,这需要将无功功率的定义式代入瞬时功率表达式之后通过在合理时间区间上的积分从而可确定电抗性元件储存的能量。
[1] 段大鹏,孙玉坤,尹鹏军,等. 单相电路电流分解与功率定义新方法[J]. 电力系统自动化,2005(5):34- 37.
[2] 陈明忠. 单相非正弦电路电流分解与功率定义的研究[J]. 江苏电器, 2008(7):24- 28.
[3] 熊元新,陈允平.正弦电路瞬时功率理论研究[J]. 电网技术,2001(6):18- 20.
[4] Zhang Dairun . Power Components in Single- phase AC Circuit[J]. Transactions of China Electrotechnical Society,1998,13(2):53- 56.
[5] Robbins Allan H, Miller Wilhelm C . Circuit Analysis Theory and Practice[M].4th ed.Kentucky:Cengage Learning Inc,2012:642- 643.
[责任编辑:张永军]
Study of Relashionship Between Reactive Power and Energy Stored by Reactive Components in AC Circuit
WANG Sheng- jie1,ZHAN Jin- hua2,HU Guo- hua1
(1.School of Electronic Information and Engineering, Hefei University, Hefei 230601;2.Police Command Department,Hefei Public Security Bureau,Hefei 230041,China)
In AC circuit, there are two kinds of power: active power and reactive power. In this paper, the characteristics of these two kinds of power are discussed and the conclusions about these two kinds of power are qualitatively given. Followed by the unique characteristics of reactive power, firstly, theoretical definition of reactive power for reactive elements is given out, then the relationship between energy stored by reactive element and the the theoretical definition of reactive power is discussed. Finally the theoretical derivation shows that the reactive power is different from the active power in sinusoidal AC circuit, the reactive power is not the average value of instantaneous power and the energy storage of the reactive element can be obtained by integrating the reactive power.
AC circuit; active power; reactive power; energy stored by reactive elements
2016-10-12
2017-02-23
合肥学院2016院自然科学科研发展基金项目(0395841698)、安徽省高等学校省级质量工程项目(2015sxzx018,2015ckjh062)、安徽省教育厅自然科学基金重点项目(KJ2015A164)、安徽省高等学校省级质量工程项目(2016jyxm0884)资助。
汪圣杰(1989— ),男,安徽太湖人,合肥学院电子信息与电子工程系助教,研究方向:电路原理、微波技术、天线,嵌入式;詹金华(1979— ),男,安徽太湖人,合肥市公安局警令部副主任科员。
TM132
A
2096-2371(2017)02-0047-04
