数形结合思想在高中数学教学中的运用

2017-05-15崔孝禹

青苹果 2017年6期

文/崔孝禹

数形结合思想在高中数学教学中的运用

文/崔孝禹

随着教育教育的不断深化，课堂教学以学生为主体的教育思想逐渐得到教师群体的肯定。在日常教育活动中，教师需要灵活使用数形结合思想，优化教育方案激发学生创新思维，进而实施预期的教育目标。文章主要以人教版高中数学教材为例，对数形结合思想在高中数学教学中的运用进行分析。

数学作为一门逻辑性较强的课程，也是解析数量关系及图像的科目，对于高中生来说，数学知识学习比较枯燥，学习难度比较大。因此，在高中数学课程教育活动中，教师必须要依据教材知识，采取切实可行的教学方法，引导学生对数学知识进行解析，进而获得优质的教育效果。

1 现阶段高中数学课程教学存在的不足

1.1 学习思维较为肤浅

现阶段，我国高中数学课程教育活动中，由于学生对数形结合概念认知比较肤浅，导致课程教学质量比较低效。具体体现在高中生在解决问题过程中，只会依据数学题目与问题解析数学条件，没有意识到转换解题思维，导致学生数学思维一直处于停滞不前的状态。同时，高中生普遍存在抽象思维，学生往往只会解答一些比较直观的数学问题，面对一些比较抽象的数学问题，学生无法准确把握问题核心，进而严重影响到课程教学质量。

1.2 学习差异性

因为高中教育阶段学生的学习基础是不一样的，促进学生的学习思维也存在一定差异，在思考问题的方式与视角上也有所不同。这也就进一步决定学生对同一问题的解析认知存在一定区别，促使学生的数学思维产生区别。但是，高中生在实际解答问题过程中，一般情况下不会自主挖掘数学条件，对提升课程教学效率与质量而言是十分不利的。

2 数形结合思想在高中数学教学中的运用

2.1 集合问题

借助图示实现将数学问题中无形的物质转化成有形，再将有形的东西转化成方程去求解。通过有效弱化学习难度，有效树学生的学习信心。因此，教师在教学集合知识时，需要充分利用数形结合方法，利用韦恩图去解决集合问题，进而不断强化学生解决问题的能力。需要注意的是在实际解答集合题时需要侧重关注数与行的结合。

例1：某班有54名同学，其中会打篮球的共有36人；会打排球的人数比会打篮球的多4人；另外，这两种球都不会打的人数是都会打的人数1/4还少1，问既会打篮球又会打排球的有______人.

分析：用韦恩图画出示意图，借助图形去分析解决此问题，使复杂的问题简单化，借助方程去求解。解析∵会打篮球的共有36人；会打排球的人数比会打篮球的多4人， ∴会打排球的有40人，设既会打篮球又会打排球的有x人，则只会打篮球的有篮球的有36-x人，只会打排球的有40-x人，则会打球的人有36+40-x=76-x，不会打球的人有54-（76-x）=x-22， ∵这两种球都不会打的人数是都会打的人数的1 4 还少1， ∴x-22= 1 4 x-1，即 3 4 x＝21，解得x=28，故答案为：28

通过有效利用数形结合方法，有效将数学问题的隐性条件进行显示，促使解题过程变得更为直观化，便于学生更加有效内化知识，激发学生的学习兴趣，进而充分发挥出数形结合教育方法的直观性功能。

2.2 方程不等式

随着学习程度的不断加深，高中生数学知识体系与认知能力日趋完善，学生的数学思维也变得更为成熟。从内心视角进行分析，思维作为学生头脑中接受客观事实刺激后对数学知识体系的发展规律完整细致的概括过程。借助对高中数学知识中“数”与“形”的深度剖析，进而有效形成一整套科学思维方式。

例2，对于每一个实数x，f（x）是y=2x与y=-x+1这两个函数中的较小者，则f（x）的最大值（）

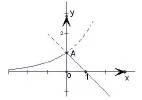
本题主要考察学生对一次函数的性质与应用，指数函数的解析式及定义（定义域、值域）等考点的理解。在实际解答过程中，要求学生分别画出函数y=2x与y=-x+1的图象，如图所示，实线部分即是函数f（x）的图像，由图像知函数f（x）的最大值是1，无最小值， ∴函数f（x）的最大值是1.

2.3 函数问题

在高中教学过程中，数学函数分析过程中，需要结合函数问题为根据，利用数学图像的方式将其中的函数知识进行详细分析，研究其中的函数知识。因为数学函数知识与图像之间具有紧密的联系，能够结合函数中的数量特征，进行巧妙的运用，凸显函数运行中的知识点，帮助老师更好的分析其中的函数特征，更好的进行函数图像观察，从而掌握详细的函数规律。

例3证明：如果函数y=f（x）满足f（a+x）=f（a－x），则f（x）的图像关于直线x=a对称。

解析：证明函数图像的对称性，一般地可以转化为图像上点的对称性来处理；本题证明f（x）的图像关于直线x=a对称，可在f（x）的图像上任取一点P，证明P关于直线x=a的对称点Q也在该函数图像上即可。

证明：在y=f（x）的图像上任取一点P（x,y），P点关于x=a的对称点为Q（2ax,y），则f（2a－x）=f［a+（a－x）］=f［a－（ax）］=f（x），故Q点坐标也满足y=f（x），故Q点也在该曲线上，因此可得：f（x）的图像关于直线x=a对称。通过有效结合图形进行直观感知，一方面有助于理解和记忆函数的性质，另一方面有助于得到解题思路，获得快捷的解题方法。