改进组合式T形钢管内核心混凝土应力-应变关系

曹 兵, 戴绍斌, 黄 俊, 陶 李

(1.安徽工程大学 建筑工程学院,安徽 芜湖 241000; 2.武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)

改进组合式T形钢管内核心混凝土应力-应变关系

曹 兵1, 戴绍斌2, 黄 俊2, 陶 李1

(1.安徽工程大学 建筑工程学院,安徽 芜湖 241000; 2.武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)

文章基于改进组合式T形钢管混凝土柱轴压试验结果,详细分析了在轴压状态下钢管对核心混凝土的约束特点,通过截面合理划分和假定,并借鉴已有的箍筋约束混凝土应力-应变关系,提出了改进组合式T形钢管内核心混凝土应力-应变关系;在分析主要影响参数的基础上,给出了应力-应变关系参数计算表达式;采用有限元软件ABAQUS对改进组合式T形钢管混凝土柱轴压荷载-应变关系曲线进行了数值计算,并将有限元计算结果与试验结果进行对比。研究结果表明,有限元计算结果与试验结果吻合较好,验证了所提核心混凝土应力-应变关系的合理性。

组合式T形钢管;核心混凝土;约束特点;应力-应变关系;有限元

钢管混凝土是在箍筋约束混凝土的基础上演变而来的,不同截面形式的钢管混凝土构件,其钢管对核心混凝土的约束作用明显不同,导致了钢管混凝土构件在力学性能方面存在差异。目前,国内外研究者采用试验研究和数值分析2种方法对钢管混凝土构件力学性能进行了大量的研究[1]。相比于试验研究法,数值分析法更加快捷方便,能够有效地解决试验研究中无法考虑的相关因素影响问题,其关键在于如何建立合理的核心混凝土应力应变关系。

国内对不同截面钢管内核心混凝土应力-应变关系的研究已有一些成果。文献[2]采用分解分析法对圆形截面钢管混凝土柱试验曲线进行了研究,提出了圆形截面钢管内核心混凝土应力-应变关系;文献[3]在方形截面钢管混凝土柱试验研究的基础上,充分考虑了约束效应系数的影响,提出了方形截面钢管内核心混凝土应力-应变关系;文献[4]对矩形截面钢管内核心混凝土应力-应变关系进行了研究,提出了基于体积的核心混凝土强、弱约束区划分法,建立了矩形截面钢管内核心混凝土应力-应变关系;文献[5]对带约束拉杆T形截面钢管混凝土柱进行了试验研究,分析了带约束拉杆T形截面钢管对核心混凝土的约束特点,将钢管对核心混凝土的约束作用等效为有效侧向约束力,借鉴箍筋混凝土应力-应变关系,提出了带约束拉杆T形截面钢管内核心混凝土应力-应变关系;文献[6]在对多室式T形截面钢管混凝土柱试验研究的基础上,采用等效截面法建立了多室式T形截面钢管内核心混凝土应力-应变关系。

以上的研究成果表明,采用有限元软件对异形截面钢管混凝土柱进行全过程分析时，仍采用普通截面钢管内核心混凝土的应力-应变关系是不尽合理的。因此,对改进组合式T形截面钢管内核心混凝土应力-应变关系需做进一步研究。

本文在改进组合式T形钢管混凝土柱轴压试验研究成果[7]的基础上,详细分析了钢管对核心混凝土的约束特点,通过合理假定,将截面划分为矩形区域和方形区域,借鉴箍筋约束混凝土应力-应变关系,提出了改进组合式T形截面钢管内核心混凝土应力-应变关系,最后采用有限元软件ABAQUS对改进组合式T形钢管混凝土柱轴压荷载-应变关系曲线进行了计算,并与试验结果进行了对比分析,验证了所提应力-应变关系的合理性。

1 钢管对核心混凝土的约束特点

在钢管混凝土中,钢管对核心混凝土的约束作用依据截面形式的不同而有所不同,改进组合式T形截面钢管对核心混凝土约束模式主要分为2种,如图1所示。

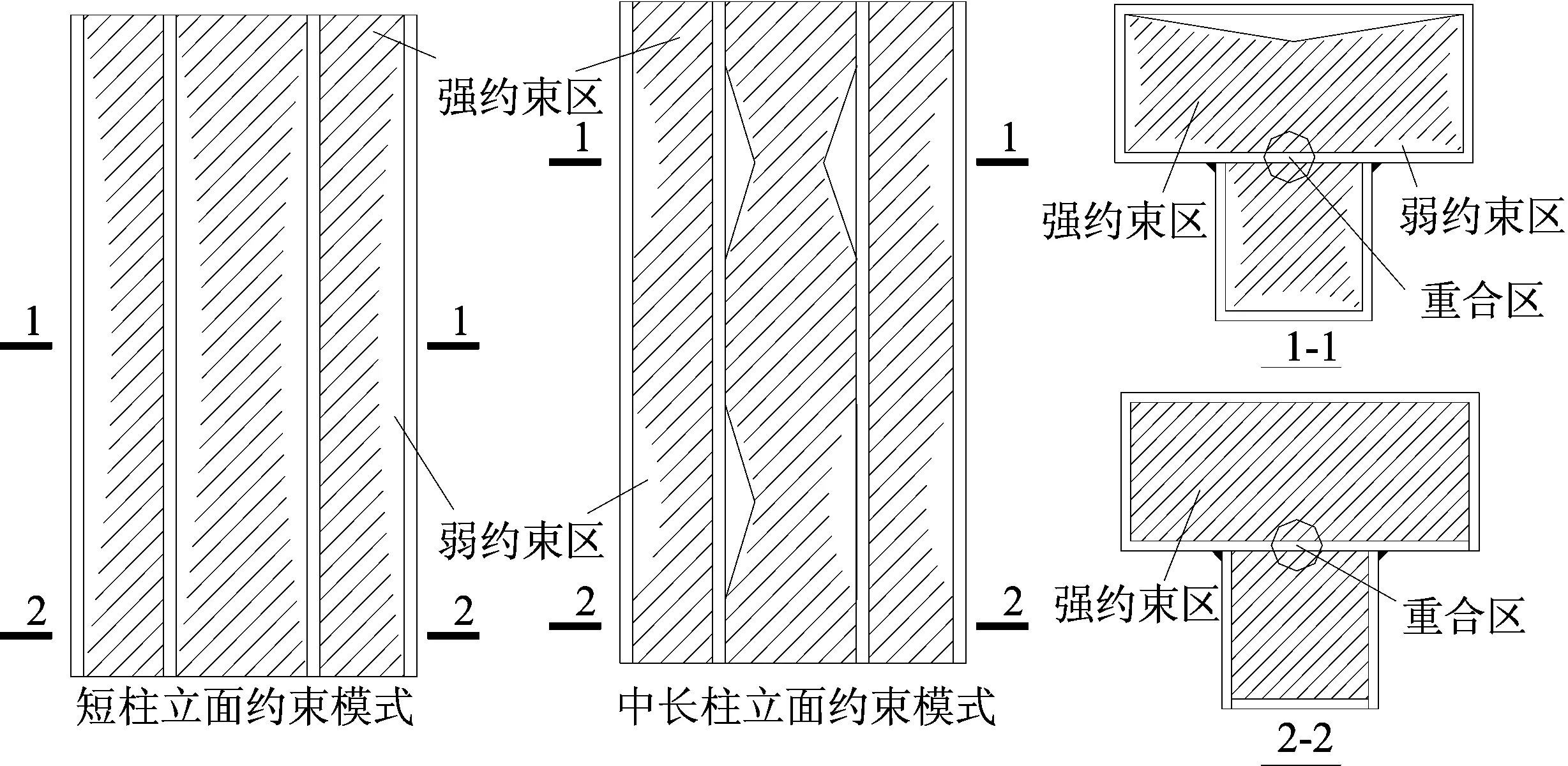
图1 钢管对核心混凝土约束示意图

从图1可以看出,短柱中钢管对核心混凝土的约束作用主要集中在端部区域,中部区域约束作用较弱;中长柱中钢管对核心混凝土的约束作用主要集中在端部以及中部区域,其他区域约束作用较弱;对于1-1截面,钢管对核心混凝土的约束作用主要集中在角部,钢管各边中部主要依靠钢板的抗弯刚度约束核心混凝土的外凸变形,约束作用相对较弱,同时钢管的宽厚比越大,这种约束作用越小,主要是由于宽厚比较大的钢管在轴向荷载作用下横向外凸变形无法得到抑制,从而容易先发生局部屈曲;对于2-2截面,钢管对核心混凝土的约束作用均匀分布在截面各边,主要是由于端部四周焊缝对钢管产生了加强作用,有效约束了钢管的横向变形;对于1-1截面和2-2截面中的重合区,钢管对核心混凝土均具有强约束作用,主要是由于钢板两侧均存在核心混凝土,在轴向荷载作用下两侧核心混凝土均具有相对运动趋势,从而对钢板产生了相反方向的侧压力。

2 核心混凝土应力-应变关系

2.1 应力-应变关系的提出

箍筋约束混凝土本构模型能够较好地描述不同约束水平下约束混凝土的力学性能,钢管混凝土在实质上类似于箍筋约束混凝土,两者之间的区别仅在于箍筋只承受环向拉力,钢管需承受环向拉力、纵向压力和径向压力,处于较为复杂的三向应力状态,但钢管所受的径向压力相对较小,可以忽略,钢管处于平面应力状态,屈服时均服从von Mises平面屈服准则[2,8-10]。本文在文献[2,7-10]的基础上,结合改进组合式T形截面钢管混凝土约束特点及应力-应变关系曲线特点,提出改进组合式T形截面钢管内核心混凝土应力-应变关系,如图2所示,其表达式如(1)～(3)式所示。

在AB上升段,有

(1)

在BC下降段,有

σ=fcc[1+100(k-1)(ε-εcc)]

(2)

在CD水平段,有

σ=mfcc

(3)

图2及(1)～(3)式中,εcc为约束混凝土平均峰值应变;fcc为受约束混凝土平均极限抗压强度;εco为无约束混凝土峰值应变;fco为无约束混凝土极限抗压强度;Ec为混凝土弹性模量;Esec为混凝土割线模量;r为AB段曲线形状参数,r=Ec/(Ec-Esec),Esec=fcc/εcc;k为BC下降段参数;m为CD水平段参数。

图2 核心混凝土应力-应变关系

2.2 应力-应变关系参数计算

2.2.1 有效侧向约束系数

改进组合式T形截面钢管对核心混凝土的约束作用主要和钢管厚度、宽厚比、材料强度以及长细比有关,弱约束的体积、抛物线的峰值和起角均有所不同。为简化计算,在计算有效侧向约束系数时采用以下假定:① 若钢管各边比值相差不大时(如a/b<3),各区域弱约束区抛物线起角均为θ,且起角范围不大于15°;② 截开面两侧均为强约束区,不存在弱约束区;③ 中长柱中部L″范围内为非约束区,其核心混凝土体积不计入强约束区核心混凝土总体积。横截面与纵截面约束区划分如图3所示。

有效侧向约束系数采用强约束区核心混凝土体积与核心混凝土总体积之比计算,其表达式为:

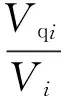
(4)

其中,kei为各区域核心混凝土的有效侧向约束系数;Vqi、Vi分别为各区域强约束区核心混凝土总体积和核心混凝土总体积。

(1) 短柱有效侧向约束系数计算。对于改进组合式T形截面钢管混凝土短柱,各区域在横截面、纵截面上的强、弱约束区划分如图3a、图3b所示,A～H面中弱约束区均相当于4个棱柱体。

对于图3a区域1,弱约束区核心混凝土总体积为:

Vr1=VAr+VBr+VCr+VDr=

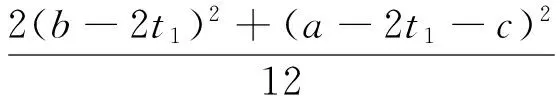
(5)

强约束区核心混凝土总体积为:

Vq1=V1-Vr1=L(a-2t1)(b-2t1)-

(6)

对于图3b区域2,弱约束区核心混凝土总体积为:

Vr2=VFr+VGr+VHr=

(7)

强约束区核心混凝土总体积为:

Vq2=V2-Vr2=

(8)

根据(4)式可得出各区域有效侧向约束系数为:

ke1=Vq1/V1=

1-(tanθ)×

(9)

(10)

(2) 中长柱有效侧向约束系数计算。对于改进组合式T形截面钢管约束混凝土中长柱,各区域在横截面、纵截面上的强、弱约束区划分如图3c、图3d所示,同理可求得改进组合式T形截面钢管约束混凝土中长柱各区域有效侧向约束系数,不再赘述。具体计算公式如下：

(11)

(12)

图3 横截面与纵截面约束区划分

2.2.2 有效侧向约束应力

在计算有效侧向约束应力时假定各区域有效侧向约束力沿管壁是均匀分布的,采用有效约束系数来考虑其不均匀性,其表达式为:

fij=keifij′

(13)

其中,i=1,2;j=1,2;fij为各区域核心混凝土各面的有效侧向约束应力;fij′为各区域核心混凝土各面的平均有效侧向约束应力。

首先以区域1为研究对象,取纵向单位长度钢管混凝土为受力体进行分析,钢管在水平方向沿长边、短边受力分析示意图如图4所示。

根据力平衡条件,平衡方程为:

f11′(a-2t1)=2fsh11t1

(14)

f12′(b-2t1)=2fsh12t1

(15)

其中,fsh11、fsh12为区域1各边钢管的平均横向应力。

图4 区域1钢管受力分析示意图

同理可求得区域2钢管平均有效侧向约束应力,不再赘述。

2.2.3 钢管的平均横向应力

钢管的宽厚比R是影响钢管混凝土破坏模态的主要因素,钢管的局部屈曲影响也主要和钢管的宽厚比R有关,钢管在双向应力作用下,即使不发生局部屈曲,其纵向应力均不能达到屈服强度[5,11-12]。改进组合式T形截面钢管约束混凝土中钢管在达到屈服强度前纵向应力fszip(i=1,2;p=1,2)与横向应力fship(i=1,2;p=1,2)的关系曲线如图5所示,钢管纵向和横向实际应力路径曲线近似于二次抛物线,钢管在双向应力作用下达到屈服强度时均服从von Mises屈服准则。因此,将文献[5,11-12]中的研究成果推广应用到改进组合式T形截面钢管混凝土柱中,达到极限荷载时钢管各边纵向应力fszip与横向应力fship的表达式如下：

当R≤0.723时,有

fszip=-0.89fy,

fship=0.21fy

(16)

当R>0.723时,有

(17)

图5 钢管纵向应力fszip与横向应力fship关系曲线

2.2.4 弱约束区抛物线起角θ

各区域钢管各边对核心混凝土的约束作用不同,弱约束区抛物线起角均不同,为简便计算,弱约束区抛物线起角均取各边起角较大值。弱约束区抛物线起角θ主要和钢管宽厚比R、约束效应系数ξ有关,通过试验数据回归计算,得到弱约束区抛物线起角θ的表达式为:

(18)

2.2.5 核心混凝土平均极限抗压强度

各区域核心混凝土受到的约束作用不同,核心混凝土平均极限抗压强度不同,为简化计算,核心混凝土平均极限抗压强度取各区域较小值,核心混凝土平均极限抗压强度采用Mander模型中建议的公式计算,其表达式为:

1.003fco-2minfij

(19)

2.2.6 核心混凝土平均峰值应变

各区域核心混凝土极限抗压强度不同,其峰值应变也有所不同。文献[9]中提出了核心混凝土峰值应变计算表达式,并采用修正系数η来修正峰值应变,其修正系数η均采用某一常数值计算。核心混凝土峰值应变与核心混凝土极限抗压强度、钢管宽厚比R、约束效应系数ξ等因素有关,通过试验数据回归计算,得到核心混凝土峰值应变的表达式为:

εcc=εco(0.001 6+11.97fco)×

(20)

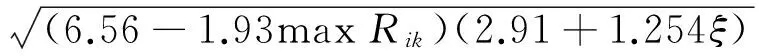
(21)

采用(20)式、(21)式对文献[7]中试件的核心混凝土平均峰值应变进行计算,并与试验值对比,如图6所示。

图6 平均峰值应变计算值与试验值对比

由图6可知，平均峰值应变计算值与试验值接近程度较好,计算值与试验值的比值平均值为0.973,标准差为0.023,表明(20)式、(21)式能够有效地计算出改进组合式T形截面钢管内核心混凝土的平均峰值应变。

2.2.7 下降段参数k

核心混凝土在达到峰值应力后,应力-应变曲线开始出现下降段,但其下降趋势不同,文献[10]采用下降段参数k来描述核心混凝土应力-应变曲线下降段的平缓程度。

此平缓程度主要和约束效应系数ξ、长细比λ等参数有关,通过试验数据回归计算,得到下降段参数k的表达式为:

(22)

2.2.8 水平段参数m

核心混凝土在达到峰值应力后,应力-应变曲线开始出现下降段,但同时由于钢管对核心混凝土的约束作用,曲线下降段渐趋于平缓,应力不再下降,应变一直增大,接近于水平状态。此水平段参数m主要和约束效应系数ξ、长细比λ等参数有关,通过试验数据回归计算,得到水平段参数m的表达式为:

(23)

3 应力-应变关系验证

为了验证本文所提改进组合式T形截面钢管内核心混凝土应力-应变关系的合理性,将所提应力-应变关系应用到有限元软件ABAQUS中,并对文献[7]中部分试件轴压荷载-应变关系曲线进行了计算,对比结果如图7所示。

从图7可以看出,有限元计算的轴压荷载-应变关系曲线与试验所得曲线吻合程度较好,有限元计算轴压极限荷载基本上小于试验轴压极限荷载,总体上偏于安全,轴压极限荷载有限元计算值与试验值之比为0.957～0.998,平均值为0.983,均方差为0.018,表明所提应力-应变关系具有一定的合理性,也适用于改进组合式T形钢管混凝土柱试件的有限元分析。

图7P-ε有限元计算曲线与试验曲线对比

4 结 论

(1) 通过截面的合理划分和假定,提出了改进组合式T形截面钢管内核心混凝土应力-应变关系,基于体积的核心混凝土强、弱约束区划分方法改进了箍筋约束混凝土应力-应变关系中有效侧向约束系数的计算方法,依据试验结果回归计算得到改进组合式T形截面钢管内核心混凝土应力-应变参数计算表达式。

(2) 有限元计算的轴压荷载-应变关系曲线与试验所得曲线吻合程度较好,有限元计算轴压极限荷载基本上小于试验轴压极限荷载,总体上偏于安全;轴压极限荷载有限元计算值与试验值之比为0.957～0.998,平均值为0.983,均方差为0.018,验证了所提改进组合式T形截面钢管内核心混凝土应力-应变关系的合理性。

[1] 王成刚,柳炳康,王静峰,等.方、圆钢管再生混凝土柱抗震性能试验研究与对比分析[J].合肥工业大学学报(自然科学版),2016,39(7):949-954.

[2] 钟善桐.钢管混凝土结构[M].3版.北京:清华大学出版社,2003:48-58.

[3] 韩林海.钢管混凝土结构:理论与实践[M].北京:科学出版社,2004:68-71.

[4] 郭小平.矩形钢管混凝土中核心混凝土的本构关系[J].湖南交通科技,2011,37(2):74-79，189.

[5] 左志亮,蔡健,钟国坤,等.带约束拉杆T形截面钢管内核心混凝土的等效单轴本构关系[J].工程力学,2011,28(11):104-113.

[6] 屠永清,刘林林,叶英华.多室式钢管混凝土T形短柱的非线性分析[J].工程力学,2012,29(1):134-140.

[7] 曹兵,戴绍斌,黄俊.改进组合式T形钢管混凝土柱轴压性能试验研究[J].建筑结构学报,2014,35(11):36-43.

[8] SHANMUGAM N E,LAKSHMI B.State of the art report on steel-concrete composite columns[J].Journal of Constructional Steel Research,2001,57(10):1041-1080.

[9] MANDER J B,PRIESTLEY M J N,PARK R.Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,1988,114(8):1807-1826.

[10] SCHNEIDER S P.Axially loaded concrete-filled steel tubes[J].Journal of Structural Engineering,1998,124(10):1124-1138.

[11] GE H B,USAMI T.Strength analysis of concrete filled thin-walled steel box columns[J].Journal of Constructional Steel Research,1994,30(3):259-281.

[12] SAKINO K,NAKAHARA H,MORINO S,et al.Behavior of centrally loaded concrete-filled steel-tube short columns[J].Journal of Structural Engineering,2004,130(2):180-188.

(责任编辑 张淑艳)

Stress-strain relationship for core concrete of improved composite T-shaped steel tube

CAO Bing1, DAI Shaobin2, HUANG Jun2, TAO Li1

(1.College of Civil Engineering and Architecture, Anhui Polytechnic University, Wuhu 241000, China; 2.School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, China)

Based on the axial compressive experimental results of improved composite T-shaped concrete-filled steel tubular columns, the constraint characteristic of steel tube to core concrete under axial compressive load was analyzed. According to the existing stress-strain relationship for stirrup confined concrete, the stress-strain relationship for the core concrete of improved composite T-shaped steel tube was proposed by reasonable section division and assumption. Based on the analysis of the key influencing parameters, the parameter calculation expressions of stress-strain relationship were given. Then the load-strain curves of the improved composite T-shaped concrete-filled steel tubular columns were analyzed with the proposed stress-strain relationship by using finite element software ABAQUS, where the results calculated by ABAQUS were compared with the experimental results. It is shown that the results calculated by ABAQUS agree well with the experimental results, thus verifying the rationality of the proposed stress-strain relationship.

composite T-shaped steel tube; core concrete; constraint characteristic; stress-strain relationship; finite element

2015-09-02；

2017-02-23

安徽省自然科学基金资助项目(1708085QE121);安徽省高等教育提升计划资助项目(TSKJ2016B25);安徽工程大学科研启动基金资助项目(2015YQQ013)和安徽省大学生创新创业训练计划资助项目(201610363116)

曹 兵(1988-),男,安徽安庆人,博士,安徽工程大学讲师; 戴绍斌(1966-),男,湖北仙桃人,博士,武汉理工大学研究员,博士生导师.

10.3969/j.issn.1003-5060.2017.04.017

TU398.9

A

1003-5060(2017)04-0515-07