测电源电动势和内阻实验数据的处理方法

许文

测电源的电动势E与内阻r的实验涉及到电路的设计、器材的选择、实物连线、数据处理、结果求解、误差分析等典型问题，具有方法灵活、内涵丰富、综合性强、考查频度大等特点，深受高考命题者的青睐。该实验原理是闭合电路的欧姆定律，而闭合电路欧姆定律的数学表达式有几种不同的表达形式，因此这个实验有很多变化之处与创新之点，特别是关于实验数据的线性图像处理技巧，要求学生能够明确实验原理，并能基于用线性图像处理实验数据的要求对欧姆定律的表达式进行数学推导变换，再通过线性图像的物理意义，对问题灵活地分析与求解。本实验能很好的考查学生的实验迁移能力和创新能力。本文通过对典型实例的分析，帮助学生认识该实验的创新设计思路与用线性图像处理数据的方法，希望给考生的实验备考复习带来一些启迪。

1 伏安法

1.1 实验原理

U=E-Ir。

1.2 电路设计

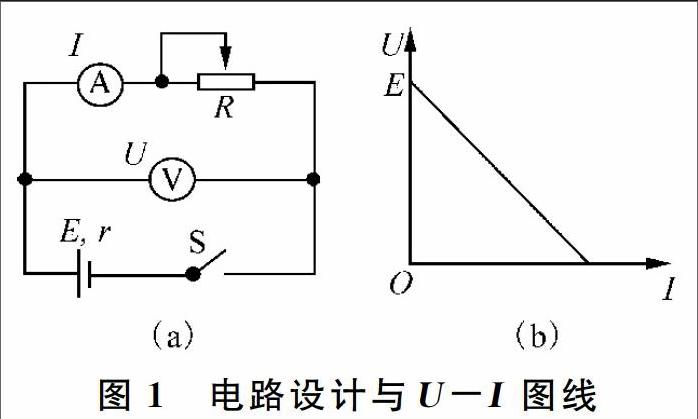
伏安法电路设计一般如图1（a）所示。

1.3 数据处理

改变R的值，测出多组U、I值，作出U-I图线，如图1（b）所示。图线与U轴交点的纵坐标即为电源电动势E的大小，电源内阻r为图线斜率的相反数。

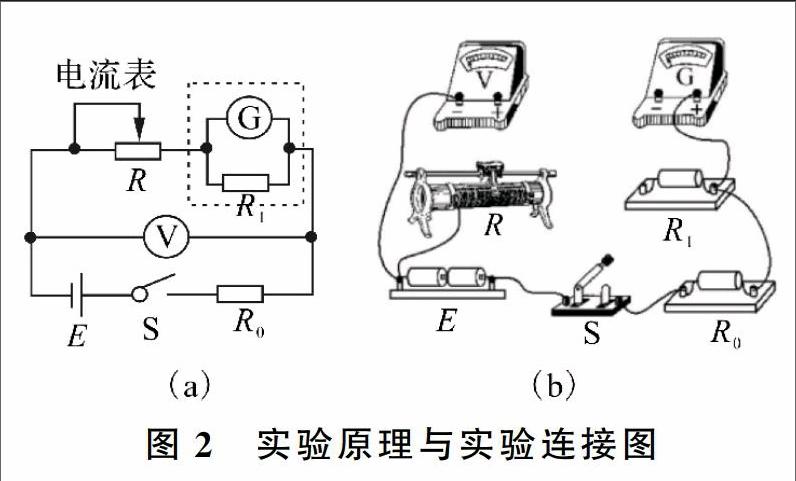
例1：某研究性学习小组利用伏安法测定某一电池组的电动势和内阻，实验原理如图2（a）所示，其中，虚线框内为用灵敏电流计G改装的电流表A，V为标准电压表，E为待测电池组，S为开关，R为滑动变阻器，R0是标称值为4.0 Ω的定值电阻。

（1）已知灵敏电流计G的满偏电流Ig=100 μA、内阻rg=2.0 kΩ，若要改装后的电流表满偏电流为200 mA，應并联一只______Ω（保留一位小数）的定值电阻R1。

（2）根据图2中实验原理图，用笔画线代替导线将图2（b）连接成完整电路。

（3）某次实验的数据如下，见表1：该小组借鉴“研究匀变速直线运动”实验中计算加速度的方法（逐差法），计算出电池组的内阻r=_________ Ω（保留两位小数）；为减小偶然误差，逐差法在数据处理方面体现出的主要优点是_________ 。

（4）该小组在前面实验的基础上，为探究图2（a）所示的电路中各元器件的识记阻值对测量结果的影响，用一已知电动势和内阻的标准电池组通过上述方法多次测量后发现：电动势的测量值与已知值几乎相同，但内阻的测量值总是偏大。若测量过程无误，则内阻测量值总是偏大的原因是___________ 。（填选项前的字母）

A.电压表内阻的影响

B.滑动变阻器的最大阻值偏小

C.R1的识记阻值比计算值偏小

D.R0的识记阻值比标称值偏大

解析：（1）改装电流表扩大量程I=Ig+IgrgR1，则R1=IgrgI-Ig=1.0 Ω。

（2）连接图如图3所示。

（3）电流表相邻两次读数之差为ΔI=20 mA，r+R0=-（U5+U6+U7+U8）-（U1+U2+U3+U4）16ΔI=5.66 Ω，可得r=1.66 Ω。这样做的优点是可以充分利用每一组数据。

（4）由题给出“用一已知电动势和内阻的标准电池组通过上述方法多次测量后发现：电动势的测量值与已知值几乎相同”，这说明电压表内阻很大，其分流作用很小可以忽略不计。如果电压表的分流作用不可忽略，这会导致电源电动势与内阻的测量值均偏小，故A选项错误；滑动变阻器的作用是调节电路中总电阻的变化，不会对实验测量带来误差，B选项错误；R1实际值偏小，计算值偏大，会导致计算电流时电流值偏小。设与灵敏电流计G并联的电阻的计算值为R1，实际值为R1′（R1′

点评：本题中安培表由电流计G与电阻R1并联改装而成。当被测电源的内阻较小时，可用一个已知阻值的定值电阻R0与电源串联以保护电源。本题对实验数据的处理采用了“逐差法”，体现出知识的迁移能力与应用能力。该题第（4）问关于实验误差的分析是本题的一个难点，在以上的求解中采用U-I图像进行误差分析，有效地突破了这个难点。

2 伏伏法

在无电流表时，可用一只电压表测电源路端电压，用两只电压表的示数差与一定值电阻来测电流，作U1-U2图像。

例2：某同学用如图5所示的电路测量电动势和内电阻。电源电动势约为3 V，内阻为几欧姆；两只直流电压表V1、V2，量程均为0～3 V，内阻约为3 kΩ；定值电阻R0=5 Ω；滑动变阻器R的最大阻值为50 Ω。实验中移动滑动变阻器触头，读出电压表V1和V2的多组数据U1、U2，描绘出U1-U2图像，如图6所示，图中直线斜率为k，与横轴的截距为a，则电源的电动势E=___________，内阻r=___________（用k、a、R0表示）。

解析：某次实验中两电压表V1和V2的示数分别为U1、U2，由闭合电路的欧姆定律有：

U2=E-U2-U1R0r

变形得：U1=-ER0r+R0+rrU2

由测量数据绘出的U1-U2图像知，当U1=0时U2=ER0R0+r=a，k=R0+rr

解得：E=kak-1，r=R0k-1

点评：本题用V-V法测电源的E与r。在无电流表或电流表的量程不合适时，可以用双电压表与一定值电阻配合进行测电流。此方法是V-A法的深化与拓展。由测量数据绘出的U1-U2图像，应由闭合电路的欧姆定律导出相关的函数关系，结合图像的物理意义进行分析与求解。

3 安安法

在无电压表时，可用一只电流表和定值电阻来测电压，用两只电流表之和测电源的电流，作I1-I2图像。

例3：如图7所示的电路是利用两个电流表A1和A2测量干电池电动势E和内阻r的电路原理图。图中S为开关，R为滑动变阻器，固定电阻R1和A1内阻之和为10 000 Ω（比r和滑动变阻器的总电阻都大得多），A2为理想电流表。实验中移动滑动变阻器的触头，测出一组A1表与A2表的示数，见表2。

以I1为纵坐标、I2为横坐标画出所对应的I1-I2曲线。利用所得曲线求的电源的电动势E=___________V，内阻r=___________Ω（保留两位小数）。

解析：设某次测量时A1表与A2表的示数分别为I1、I2。由闭合电路的欧姆定律得：E=I1（R1+RA1）+（I2+I1）r

由于A2为理想电流表，且R1和A1内阻之和比r和滑动变阻器的总电阻都大得多，则有：

I2I1。

可得：I1=ER1+RA1-rR1+RA1I2

将表2中数据作出如图8所示的图线。

由图线知I1-I2图线在纵轴上的截距为：

ER1+RA1=1.49

直线的斜率的绝对值为：

rR1+RA1=0.6×10-3

得：E=1.49 ，r=0.60 Ω。

点评：本题用A-A法测电源的E与r。在无电压表或电压表的量程不合适时，可以用一电流表与一定值电阻配合进行測电压，此方法也是V-A法的深化与拓展。问题求解时要明确实验原理与实验条件。本题的实验原理是E=I1（R1+RA1）+（I2+I1）r，但由于实验条件是A2为理想电流表，且R1和A1内阻之和比r和滑动变阻器的总电阻都大得多，则有：I2I1，可得I1=ER1+RA1-rR1+RA1I2。这就是由测量数据绘出的I1-I2图像的函数关系式，再结合图像的物理意义进行分析与求解。

4 安阻法

4.1 实验原理

E=I（R+r）。

4.2 电路设计

安阻法电路设计如图9（a）所示。

4.3 数据处理

方法1：将原理表达式变形为R=EI-r，改变R的值，测出多组R、I值，作出R-1/I图线，如图9（b）所示。图线与R轴交点的纵坐标即为电内阻的相反数-r，图线斜率的绝对值即为电源电动势E的大小。

方法2：将原理表达式变形为1I=1ER-rE，改变R的值，测出多组R、I值，作出1/I-R图线，如图9（c）所示。此直线的斜率的倒数为电动势E值，直线在纵轴上的截距的绝对值乘以电动势E为电源内阻r。

例4：利用如图10所示电路，可以测量电源的电动势和内阻，所用的实验器材有：待测电源、电阻箱R（最大阻值999.9 Ω）、电阻R0（阻值3.0 Ω）、电阻R1（阻值3.0 Ω）、电流表A（量程为200 mA、内阻为RA=6.0 Ω）、开关S。实验步骤如下。

（1）将电阻箱阻值调到最大，闭合开关S。

（2）多次调节电阻箱，记下电流表的示数I和电阻箱相应阻值R。

（3）以1I为纵坐标，R为横坐标，作1I-R图线（用直线拟合）。

（4）求出直线的斜率k和在纵轴上的截距b。回答下列问题：

①分别用E和r表示电源的电动势和内阻，则1/I与R的关系式为___________。

②用实验得到的部分数据在1I-R坐标系中描出点如图11所示。作出1I-R图线，根据图线求得斜率k=___________A-1Ω-1，截距b=___________A-1。

③根据图线求得电源电动势E=___________V，内阻r=___________Ω。

解析：①由闭合电路的欧姆定律知I与R的关系为：

E=IRA+（I+IRAR1）（r+R0+R）

将上式变形并代入相关数据有：

1I=（R1+RA）（R0+r）+R1RA+（R1+RA）RER1

=3RE+3r+15E

②1/I-R图线如图12所示，k=1 A-1Ω-1；截距b=6A-1。

③1/I与R的图线是直线，直线的k斜率为：

k=3/E=1，则E=3 V。

直线在纵轴上的截距为：3r+15E=b=6。

可得：r=1.0 Ω。

点评：本题用A-R法测电源的E与r。实验电路设计对安培表的量程进行了扩展，且用定值电阻R0与电源串联保护电源。由实验原理知I与R的关系不是线性关系，不符合我们通常用函数图像处理实验数据的习惯，需要从数学上分析I与R的关系，将图线化曲为直进行转化，再结合线性图像的物理意义进行求解。

5 伏阻法

5.1 不知伏特表内阻，可用并联式

具体电路设计如图13（a）。

（1）实验原理：E=U+URr。

（2）数据处理：将原理表达式变形为1U=1E+rE·1R，改变R，测出多组R、U值，作出1/U-1/R图线，如图13（b）所示。图线与1/U轴交点的纵坐标为电动势的倒数，即：

1/E，图线斜率的绝对值即为r/E。

5.2 已知伏特表内阻，可用串联式

具体电路设计如图14（a）所示。

（1）实验原理：E=U+URV（r+R）。

（2）数据处理：将原理表达式变形为1U=1E+rERV+1ERVR，改变R，测出多组R、U值，作出1/UR图线，如图14（b）所示。图线与1/U轴交点的纵坐标为1E+rERV，图线斜率的绝对值即为1ERV。

例5：要测量一电源的电动势E（小于3 V）和内阻r（约1 Ω）。现有下列器材：电压表V（0～3 V）、电阻箱（0～999.9 Ω）、定值电阻R0=2 Ω、开关和导线。某实验小组根据所给器材设计了如图15甲所示的实验电路。

（1）电路中定值电阻R0的作用是保护___________（填“電源”或“电压表”）。

（2）A同学调节电阻箱阻值R，读出对应的电压表读数U，得到两组数据：R1=2.0 Ω时，U1=224 V；R2=4.0 Ω时，U2=2.40 V。由这两组数据可求得电源的电动势为E=___________V，内阻r=___________Ω（结果保留两位有效数字）。

（3）B同学计划用作图法处理数据，他调节电阻箱阻值R，得出了若干组数据，并描点连线得出了如图16所示的图线。图线纵坐标表示电压表读数的倒数1U。图线的横坐标表示1R+R0。若所得图线的斜率为k，在1U坐标轴上的截距为b，则该电源的电动势E=___________，内阻r=___________（用k和b表示）。

（4）比较A、B两位同学的做法，___________同学得出的结果误差更小。

解析：（1）电路中定值电阻R0的作用：在调节电阻箱时，使电路中的电流不至于太大而烧坏电源。

（2）由闭合电路欧姆定律得：I=ER+R0+r=UR+R0。

将题给数据代入得：E=2.8 V，r=1.0 Ω。

（3）将上式整理可得：1U=rE·1R+R0

+1E。

直线的斜率为：k=rE，直线在纵轴上的截距为：b=1E。

解得：E=1b，r=kb。

（4）B同学运用图像处理数据，涉及的测量数据较多，误差更小。

点评：本题用V-R法测电源的E与r。将一个已知的定值电阻R0与电阻箱串联，以避免电源的电流过大而烧坏电源。在用线性图像处理实验数据时，应根据实验原理，弄清测量的物理间的函数关系式，通过数学分析知线性图像1U-1R+R0的物理意义，问题才能顺利求解。

总之，测电源的电动势E与内阻r的实验，基本方法有V-A法、A-R法、V-R法、V-V法与A-A法。但每种方法都有一些变化点与创新之处。如无相关电表或给出的电表量程不合适时，可将电表改装或扩大其量程；当电源内阻较小时，可用已知的定值电阻与电源串联以保护电源；当电表的内阻已知时，可将电表内阻等效到为电源内阻的一部分。无论哪种方法一般都需要进行多次测量以减小实验误差。实验数据的处理通常采用线性图像法，同学们要切实加强实验基本原理的理解，从实验原理出发，并通过相应的数学变形找出两被测量相关的线性函数关系，作出线性图像，利用图像的物理意义进行分析与求解。

最后，在测电源E、r实验操作中应注意以下几点：①选用较旧电池。为了使电路的路端电压变化明显，电池的内阻宜大些。②电流不要过大，读数要快。干电池在大电流放电时，电动势E会明显下降，内阻r会明显增大。因此读电表要快，且每次读完立即断电。③要求多次测量，且测量值的变化范围要适当大些。④实验数据处理时，应从实验原理出发，用相关线性图像处理实验数据，得出E、r的平均值。