应用形态分量分析算法研究电成像测井空白条带填充

邢强, 张晋言

(中石化胜利石油工程有限公司测井公司, 山东 东营 257096)

0 引 言

微电阻率扫描成像测井得到的井周二维图像带有空白条带,无法实现全井眼覆盖,不利于后期的裂缝、孔洞提取、岩相分析和地层研究等,因此,需要对图像的空白条带进行填充。电成像测井图像空白条带填充属于图像修复范畴。目前,图像修复方法主要可分为3大类:基于偏微分方程/变分方法[1-2]、基于样本块匹配的方法[3]和基于稀疏表示的方法[4]。研究表明基于偏微分方程/变分的修复模型适合处理小区域的缺损或以结构特征为主的图像,而基于样本块匹配的修复方法可以在纹理特征大面积缺损的情况下得到较为理想的修复效果。

关于电成像空白条带填充,张团峰等[5]提出多点地质统计学Filtersim算法,以电成像图像为训练对象,对空白条带进行了填充。Tetsushi Yamada等[6]在基于电成像的孔隙度分析中,采用了Filtersim算法。孙健孟等[7]比较了反距离加权插值法和Filtersim算法。傅少庆等[8]应用Filtersim算法,填充电成像图像中非均质性强的纹理部分。王俊华[9]应用Filtersim算法在非均质性强的空白条带区域处,取得了较好的填充效果。可见,Filtersim算法已经成为电成像空白条带填充的主流方法。Filtersim算法本质上属于样本块匹配的图像修复方法,实际应用中也发现该方法在非均质强的纹理区域能得到较好的填充效果,但在结构特征为主的多层理区域,填充后的层理连续性不强。为克服这一缺陷,提出一种改进算法,以边缘图像点邻域内的线性结构强度参数为填充顺序约束,取代Filtersim中的随机序贯模拟,可提升图像中结构信息的填充效果。

S.Assous等[10]首次将基于信号稀疏表示的形态分量分析(MCA)方法应用于电成像空白条带填充。本文探讨了MCA方法的原理和实现过程,通过Flitersim算法和MCA方法的实验对比研究,发现MCA方法对于结构分量较强和纹理分量突出的2类图像,都取得了较为理想的填充效果。

图1 Filtersim和改进的Filtersim算法空白条带填充对比结果

1 改进的Filtersim算法

图1为Filtersim和改进的Filtersim算法空白条带填充对比结果。图1(b)是使用Filtersim算法对图1(a)的空白条带图像的填充结果。这里,Filtersim算法采用9×9×1搜索模板和5×5×1的patch模板,基于像素点值相似度度量,训练图像分类采用K均值聚类,初始类别数为100,多重网格数设置为2。可以看到,填充结果中出现了错误的泥质条带,原泥质条带边缘处填充结果也不好,右下角层理连接处没有较好地处理。

Filtersim算法中序贯模拟的随机性,使得在空白条带处的待模拟节点提取出为空的数据事件时,算法随机地从训练图像prototype中选择1个图案,粘贴到待模拟节点区域,导致了填充结果较差。因此,提出一种改进算法,提取空白条带的边界图像点作为初始待模拟点集合,并以边界点等照度线方向约束的数据项和信任项,约束填充顺序,优先填充边界线上高优先级的边界点,取代Filtersim中的随机序贯模拟。

1.1 实现算法

(1) 搜索原始图像,得到初始边界点集合S。

(2) 如果S为空,结束;否则执行以下步骤。

(3) 计算S集合中边界点填充优先级;由信任项C(p)和数据项D(p)乘积得到。其中,C(p)为样本块内原始硬数据节点和已经patch过的节点数量之和,表示样本块内的有效信息量。D(p)为p点处等照度线在边界法线上的投影,反映p点邻域内线性结构强度。

(4) 对集合S按照优先级进行排序,对优先级最高的边界点按Filtersim算法进行单点粘贴。

(5) 对于该次粘贴后,在patch模板边界处未曾模拟过的节点,如果不在集合S中,则将其加入集合S;遍历集合S,如果集合中节点已经被模拟过,则从集合S删除。

(6) 返回步骤(2)。

1.2 处理效果

图1(c)是采用改进的Filtersim算法对图1(a)的原始图像填充后的结果,可以看出原泥质条带边缘处和右下角层理连接处得到了较好地处理。

2 形态分量分析(MCA)方法

2.1 MCA方法原理

Starck J L等[11]提出一种将图像分解为不同形态成分,即“几何结构”和“纹理”的形态分量分解框架MCA,其重要假设是图像的几何结构和纹理分量在某个特定的基库或过完备字典下是类内稀疏的,而各形态分量稀疏表示的基库或过完备字典之间具有不相干性。通过关于结构分量和纹理分量分类稀疏表示的强稀疏性,达到图像形态分量的有效分离。

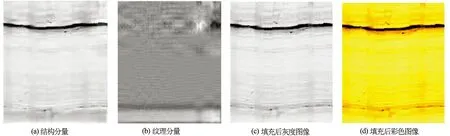
图2 MCA方法填充结果

MCA方法认为图像由边缘卡通成分(包括平滑与边缘轮廓结构)和纹理成分组成

u≅un+ut(1)

(1)

选择卡通图像un所在空间的一个基库或过完备字典Tn,则un可稀疏表示为un=Tnαn。对于纯纹理图像ut,也可通过选择合适的稀疏表征基库或过完备字典Tt,使得ut=Ttαt。利用Lagrange乘子法,再引入全变差正则化先验(TV)作为更高层的先验知识[11],对结构分量加以约束,则最终的MCA变分框架为

(2)

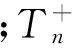
(3)

Elad M等[12]已经证明式(3)模型的收敛性。当使用稀疏系数和稀疏表征基库或过完备字典重构对应的图像分量时,各分量丢失的信息将被对应基库或过完备字典的基函数填充。

在实际应用中,MCA框架通常是按照经验选择已知稀疏表征基库或过完备字典。对于图像结构部分,常选用具有多方向性和各向异性图像表征性质的Ridgelet变换,Curvelet变换和Contourlet变换,可捕捉图像中的边缘轮廓细节信息。特别是第二代Curvelet[13]克服了高冗余度的问题,为Curvelet变换提供了更加简单的实现。对于图像的纹理部分,常选用局部离散余弦变换(Local DCT)或Gabor变换。

2.2 MCA方法实现过程

采用块协调松弛(Block-coordinate-relaxation BCR)方法求解式(3)模型[12],具体算法如下。

(1) 初始化。选择迭代次数N,TV正则化参数γ,结束标准值Stop,噪声标准偏差,Curvelet最粗略分解尺度,LDCT变换响铃及窗口宽度;对原始输入图像作Curvelet和LDCT变换,由变换系数计算初始阈值δ,计算下降步长λ。初始化结构分量Xn=0,初始纹理分量Xt=0。

(2) 迭代N次。

①计算残差R=M(X-Xn-Xt),X为待修复图像数据;

②PartA结构分量更新:

对Xn+R进行Curvelet变换,得到变换系数αn;

对αn使用δ进行软阈值收缩,再进行Curvelet反变换,重构Xn。

PartB纹理分量更新:

对Xt+R进行LDCT变换,得到变换系数αt;

对αt使用δ进行软阈值收缩,再进行LDCT反变换,重构Xt。

PartC使用参数γ对结构分量Xn进行TV校正。

③更新阈值δ,如果是指数下降,则δ=δ×λ;如果是线性下降,则δ=δ-λ。

2.3 处理结果

图2是使用MCA方法对图1(a)中原始空白条带图像填充结果。这里,迭代次数N=100,正则化参数γ=2,Stop=3,噪声标准偏差σ=0.000 001,Curvelet最粗略分解尺度为1,LDCT变换响铃为sine,窗口宽度为64;可以看到,经过填充后空白条带得到了很好的消除,与前后极板具有很好的连续性,特别是黑色泥质条带边缘的过渡更加自然。

3 处理结果对比分析

图3、图4和图5为3种方法对电成像图像填充效果对比图。可以看到,对于结构分量较强的多层理图像,如图3和图4的原始空白条带图像,Filtersim算法处理层理连接处的效果不好,如图3(b)、图4(b)所示;改进的Filtersim算法在一定程度上,对填充效果做出了提升,如图3(c)、图4(c)所示;而MCA方法对于该类图像,在3种方法中填充效果最好,极佳地保持了多个层理在空白处的连续性,如图3(d)、图4(d)所示。对于非均质性较强,纹理分量突出的原始空白条带图像(见图5),3种方法均取得了较为满意的填充效果。

图3 空白条带图像填充效果对比图(1)

图4 空白条带图像填充效果对比图(2)

图5 空白条带图像填充效果对比图(3)

4 结 论

(1) 在处理结构分量为主的多层理空白条带图像时,Filtersim算法的填充效果较差,层理连接处经常出现不连续的情况。

(2) 改进的Filtersim算法,由于采用边界点优先填充策略,取代了Filtersim算法中的序贯模拟,对于多层理图像的填充效果比Filtersim算法有了明显的提升。

(3) MCA方法从信号稀疏表示的角度,分别对图像结构信息和纹理信息进行分解和重构,处理多层理图像和非均质性较强的纹理图像,都取得了较好的填充效果。

(4) MCA方法完全是数据驱动,不依赖于任何地质模型,在使用上比Filtersim算法更加方便和高效。

参考文献:

[1] BERTALMIO M, SAPIRO G, CASELLES V, et al. Image Inpainting [C]∥International Conference on Computer Graphics and Interactive Techniques, New Orleans, 2000: 417-424.

[2] CHAN T, SHEN JIANHONG. Mathematical Models for Local Non-texture Inpaintings [J]. SIAM Journal on Applied Mathematics, 2002, 62(3): 1019-1043.

[3] 薛彦兵, 张桦, 王法玉, 等. 基于样本块的图像修补 [J]. 天津理工大学学报, 2008, 24(2): 46-48.

[4] 周亚同, 王丽莉, 唐红梅. 基于压缩感知的稀疏度自适应图像修复 [J]. 铁道学报, 2014, 36(9): 52-59.

[5] HURLEY N F, ZHANG T. Method to Generate Full-bore Images Using Borehole Images and Multipoint Statistics [J]. SPE Reservoir Evaluation and Engineering, 2011, 14(2): 204-214.

[6] YAMADA T, Quesada D, ETCHECOPAR A, et al. Revisiting Porosity Analysis from Electrical Borehole Images: Integration of Advanced Texture and Porosity Analysis [C]∥54th SPWLA Annual Logging Symposium, 2013.

[7] 孙建孟, 赵建鹏, 赖富强, 等. 电测井图像空白条带填充方法 [J]. 测井技术, 2011, 35(6): 532-537.

[8] 傅少庆, 伍东, 李斐, 等. 电成像空白条带自适应修复方法 [C]∥第十八届测井年会论文集, 2013: 391-398.

[9] 王俊华. 基于电成像测井图像处理关键技术研究 [D]. 荆州: 长江大学, 2015.

[10] ASSOUS S, WHETTON J, ELKINGTON P A S. Microresistivity Image Inpainting and Visualization [C]∥SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, USA, 2013.

[11] STARCK J L, ELAD M, DONOHO D L. Image Decomposition via the Combination of Sparse Representations and Variational Approach [J]. IEEE Transactions on Image Processing, 2005, 14(10): 1570-1582.

[12] ELAD M, STARCK J L, QUERRE P, et al. Simultaneous Cartoon and Texture Image Inpainting Using Morphological Component Analysis(MCA) [J]. Applied and Computational Harmonic Analysis, 2005, 19(3): 340-358.

[13] 隆刚, 肖磊, 陈学佺. Curvelet变换在图像处理中的应用综述 [J]. 计算机研究与发展, 2005, 42(8): 1331-1337.