基于干扰观测器的高超声速飞行器双幂次滑模控制研究

姜定国，刘 蓉，杨 帆

（1.南京航空航天大学 自动化学院，江苏 南京210016；2.南京航空航天大学 无人机研究院 中小型无人机先进技术工信部重点实验室，江苏 南京210016）

基于干扰观测器的高超声速飞行器双幂次滑模控制研究

姜定国1，刘 蓉2，杨 帆1

（1.南京航空航天大学 自动化学院，江苏 南京210016；2.南京航空航天大学 无人机研究院 中小型无人机先进技术工信部重点实验室，江苏 南京210016）

针对模型参数不确定和外界未知干扰对高超声速飞行器的影响，提出基于干扰观测器的双幂次滑模控制策略。首先利用插值拟合高超声速飞行器在巡航段的气动参数，从而建立精确的纵向模型；然后采用输入-输出反馈线性化方法，解除多变量之间的耦合关系；同时利用干扰观测器逼近未知干扰，并采用基于滑模方法解决非匹配不确定性的问题。最后，针对滑模控制中抖振的问题，加入双幂次进行改进。最后通过仿真实验验证表明，该方法可以保证闭环系统的全局稳定，并且拥有良好的跟踪性能和鲁棒性能。

高超声速飞行器；干扰观测器；双幂次；滑模；抖振

由于高超声速飞行器飞行环境大范围[1-2]变化，气动参数动态变化剧烈并存在外界气动干扰；建模得到的面向控制的飞行器模型与实际模型存在一定的不匹配，即建模的不确定性。以上原因导致高超声速飞行器存在较大的不确定性，这些不确定性将对高超声速飞行器控制的稳定性，快速性产生不利的影响。因此研究解决具有模型不确定性的高超声速飞行器动态特性分析问题，具有非常重要的意义。

目前针对高超声速飞行器不确定性问题，很多学者直接从控制器设计方面着手，不确定性视为一种扰动，将其假定在一定的范围内，并引入到控制器的设计中，如文献[3-4]。然而这种研究方法并没有分析不确定因素的物理本质，没有具体反映某一特定的不确定因素对动态系统的影响，如此对飞行器不确定参数的分析并不能精确反映出真实条件飞行器的动态特性和控制特性。文献[5-9]分别运用反步控制、滑模控制、鲁棒控制和自适应动态面控制等控制方法克服了外界干扰以及不确定因素的影响。然而，由于飞行器自身对飞行过程中系统的暂态性和飞行精度要求比较高，当外界干扰为非周期性的信号时，上述方法很难保证系统的暂态性。文献[10-11]分析了高超声速飞行器的不确定和外部干扰。文献[12]针对多输入多输出系统的不确定性干扰采取滑模的控制方法，但是抖振并没有得到明显的改善。

文中利用基于干扰观测器的双幂次的方法并加入参数不确定性的模型设计了高超声速飞行器的纵向模型的滑模变结构控制器。在反馈线性化得到的模型中加入不确定参数变化，然后设计控制器并利用Lyapunov函数验证其稳定性。为了验证该方法的有效性，对标称模型和参数摄动的模型进行仿真验证，表明基于干扰观测的双幂次滑模对高超声速飞行器的非线性控制具有指令跟踪行和鲁棒性。

1 高超声速飞行器纵向建模

1.1 非线性数学模型

该飞行器在高超声速巡航飞行条件下的纵向运动模型描述为[13-15]：

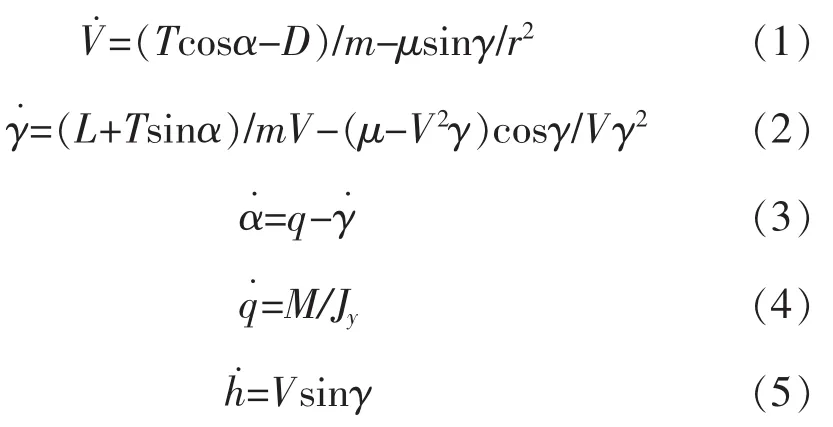
气动力和气动力矩表示为：

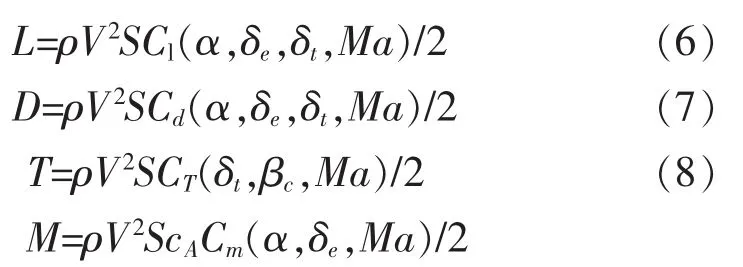
S表示机翼浸润面积，cA平均气动弦长，Cl，Cd，CT，Cm表示升力系数，阻力系数，推力系数，俯仰力矩系数。

其中，x=[V，γ，α，q，h]T表示高超声速飞行器的非线性的5个状态，分表是速度，航迹角，迎角，俯仰角速率，高度。

发动机推力计算公式为：

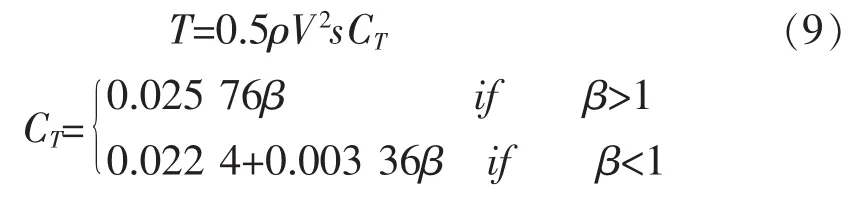
发动机动态方程采用二阶系统模型：

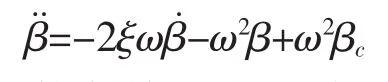
模型的控制输入为发动机节流阀调定值 βc和升降舵偏转δe，输出量为速度V和高度h，y=[V h]T，选定阻尼ζ=0.7，固有频率ωn=5 rad/s。

在分析高超声速飞行器的模型的时候，有必要考虑其内部干扰和不确定性，采用所假定的额定值附加一个变化-Δ来表示参数的不确定性，即：

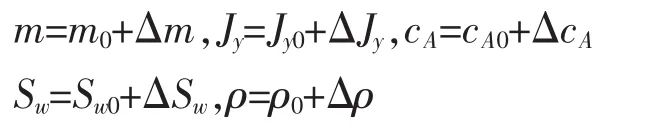
m，Jy，cA，Sw，ρ分别表示飞行器质量，转动惯量，气动弦长，机翼浸润面积和大气密度。

1.2 输入-输出反馈线性化

文中所提出的基于双幂次滑模的高超声速飞行器控制的目的是保证飞行器的飞行速度V和飞行高度h在给定的控制输入矢量范围内能快速跟踪到指定值Vc和hc。式（1）～（5）对输出飞行速度V和飞行高度h采用全状态反馈线性化处理，即对飞行

速度V和飞行高度h分别微分n和m次，直到控制输入βc或δe出现在微分式子中。于是有：

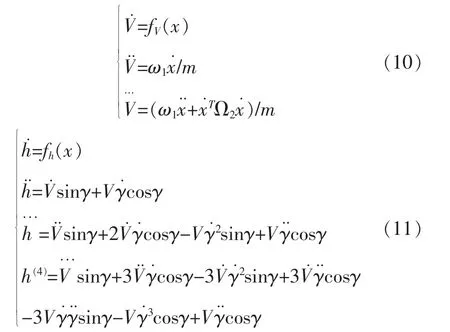
将输出飞行速度的3次微分和飞行高度h的4次微分表示为：

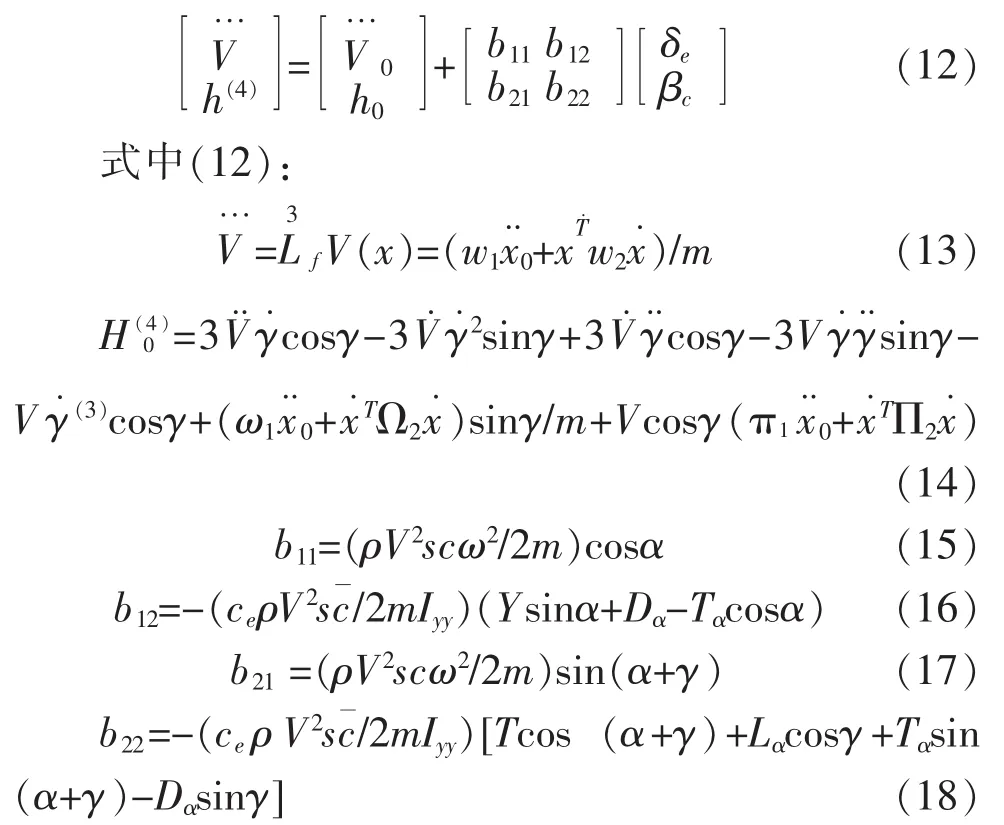
假定的额定值附加一个变化Δ的来表示参数的不确定性输出飞行速度的3次微分和飞行高度h的4次微分表示为：

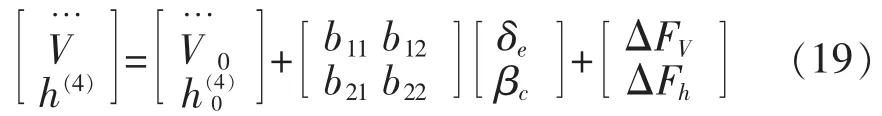
2 基于干扰观测器双幂次滑模控制器设计

2.1 控制器设计

假设:参数的确定性是有界的，|ΔFV|＜MV，|ΔFh|＜Mh（MV＞0，Mh＞0）BBT是非奇异矩阵，（BBT）-1是存在的。

根据高超声速飞行器的模型选择如下的滑模面；

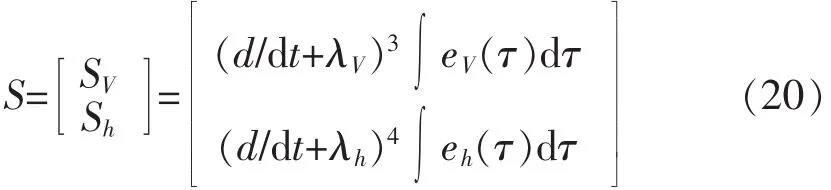
其中λV，λh是定值，eV（t）=V-Vd，eh（t）=h-hd是速度和高度的跟踪误差，积分项用来消除静态误差。

对（20）微分后：

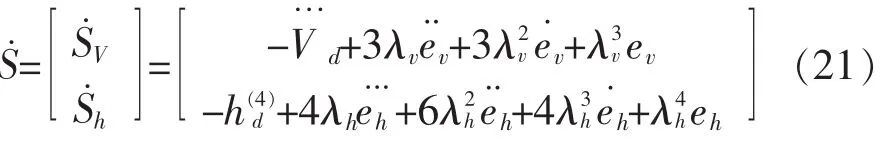
双幂次设计如下：

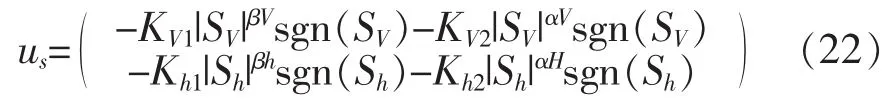
其中，kV1，kV2，kh1，kh2＞0 0＜αV，αh＜1，βV，βh＞1，sgn（SV），sgn（Sh）是符号函数。

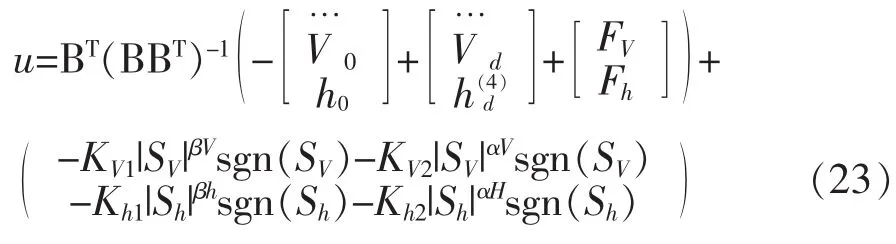
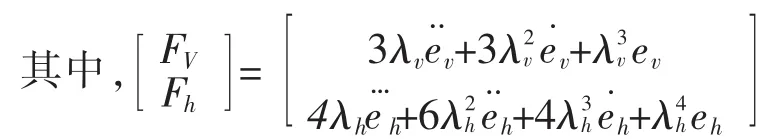
2.2 非线性干扰观测器设计

考虑系统受到的外界干扰和不确定性，令：

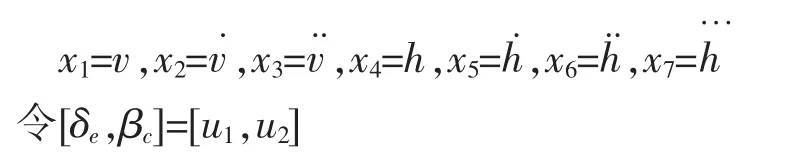
系统化为如下形式：

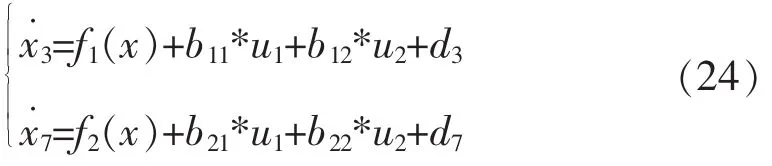
考虑速度跟踪非线性控制，设计如下的干扰观测器的状态：

设计的速度观测器为：

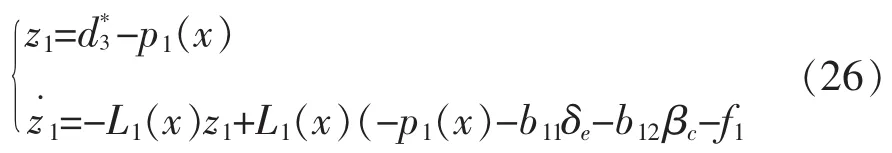
为了简化问题，通常将L1（x）取为常数l0，即：

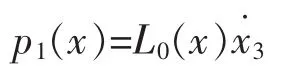
同理，高度的非线性观测器为：

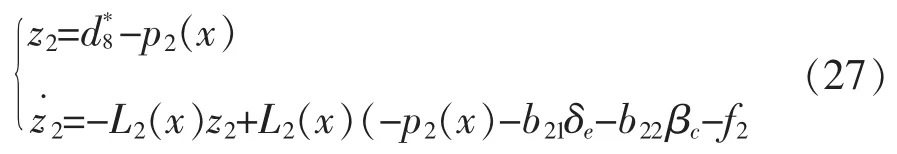
2.3 稳定性分析

选择系统Layapunov函数：

对（28）求导：

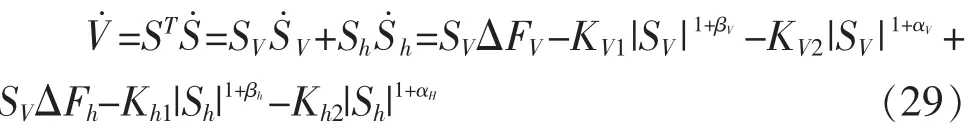
对（29）进一步推导得：

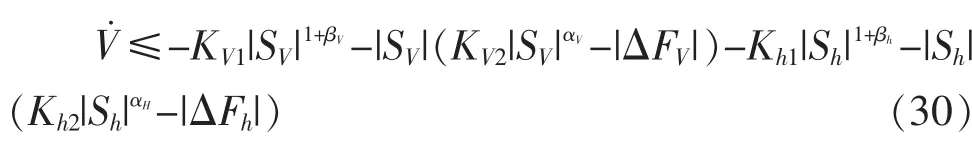
V&≤-KV1它是负定的。

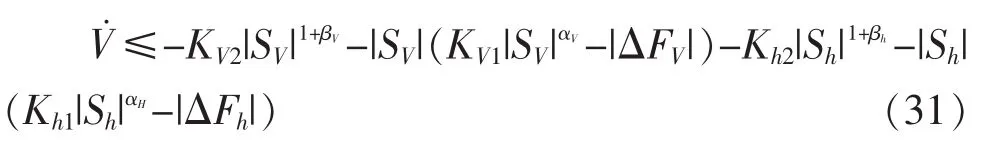
3 仿真验证

为了验证基于干扰观测器的双幂次滑模的可行性，在MATLAB/simulink下进行仿真验证，高超声速飞行器的平衡条件为：

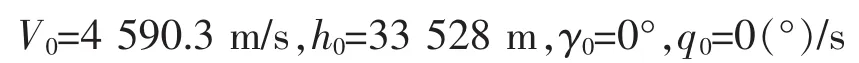
选取仿真参数如下：

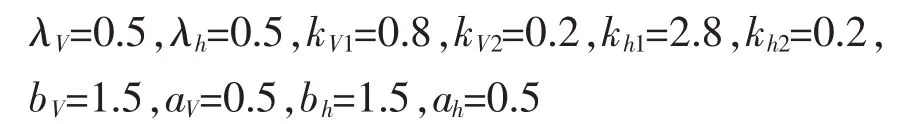
为了验证方法的鲁棒性，选取最大不确定参数变化如下：

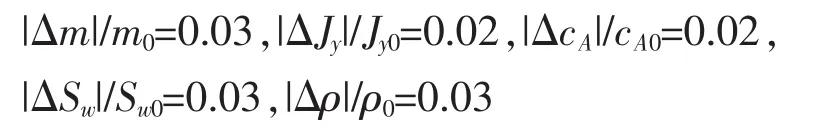
仿真结果如下：

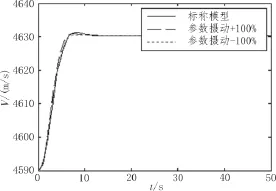
图1 标称模型和不确定性模型对速度的响应

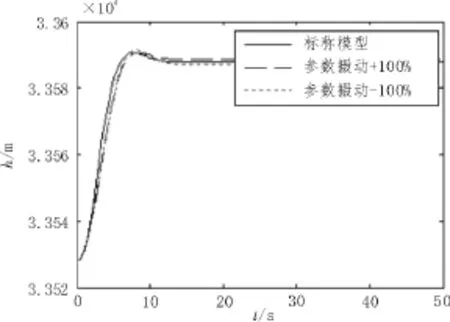
图2 标称模型和不确定性模型对高度的响应

从图1和图2看出在参数摄动在时，速度跟踪出现很小的超调，高度跟踪出现了细微的稳态误差，因此对速度和高度的单独控制取得了良好的控制效果。

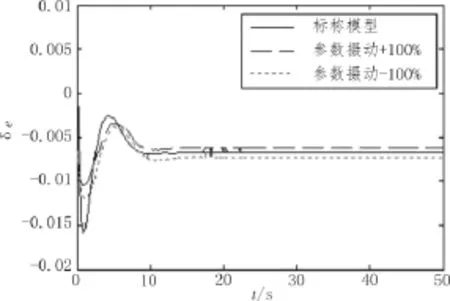
图3 标称模型和不确定性模型对升降舵的响应

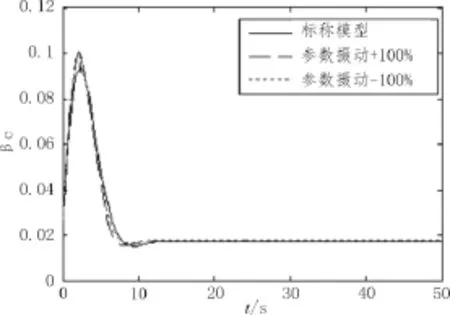
图4 标称模型和不确定性模型对调节阀的响应

从图3和图4看出，高超声速的控制输入的升降舵和调节阀具有很小的抖动，且从轨迹来看，参数摄动对轨迹变化影响小，验证了该方法具有较好的鲁棒性。仿真表明，基于干扰观测器的双幂次滑模对高超声速飞行器有较好的跟踪性和鲁棒性。

4 结 论

文中针对具有强非线性、不确定性的高超声速飞行器外环稳定跟踪控制问题，设计了基于干扰观测器的双幂次滑模非线性控制器。控制器利用了滑模方法在处理非线性问题时的独特优越性，并采用干扰观测器解决非线性干扰的问题。仿真结果表明，本文设计的控制器实现了高超声速飞行器外环稳定跟踪控制，改善了同时存在内部参数摄动和外部未知干扰下的飞行控制性能，具有良好的跟踪性能和鲁棒性能。

[1]黄琳.近空间高超声速飞行器对控制学科的挑战[J].控制理论与应用，2011，28（10）:23-28.

[2]Young M，Keith S.An overview of advanced concepts for near-space systems[R].AIAA-2009-4805，2009.

[3]刘彦斌.高超声速飞行器建模及其先进飞行控制机理的研究[D].南京：南京理工大学，2007.

[4]isa Fiorentini，Andrea Serrani，Michael A Bolender. Nonlinear control of a hypersonic vehicle with structural flexibility[C]//Proceedings of the 47th IEEE Conference on Decision and Control，2008：578-583.

[5]葛东明.临近空间高超声速飞行器鲁棒变增益控制[D].哈尔滨：哈尔滨工业大学，2011.

[6]王健.基于动态逆的高超声速飞行器高度控制方法[J].航天控制，2012，6（3）:19-22.

[7]Bajodah A H.Perturbed feedback linearization of attitude dynamics[C]//2008 American Control Conference Seattle，2008:5222-5229.

[8]韩钊，宗群，田柏苓，等.基于Terminal滑模的高超声速飞行器姿态控制[J].控制与决策，2013，28（2）：259-268.

[9]Chaofang H，Lin W.Adaptive generalized backstepping control based on sliding mode observer of air-breathing hypersonic vehicle [C]// In: Proceedings of the 31st Chinese Control Conference，Hefei，China，2012：122-128

[10]ShtesselY，TournesC，Krupp D.Reusable launch vehicle control in sliding modes[C]//In: AIAAGuidance，Navigation，andControlConference，New Orleans:AIAA，1997:335-345.

[11]R.A.Saidi，B.Minaker.An adaptive sliding mode control for trajectory tracking of aself-reconfigurable robotic system[C]//Robot Intelligence Technology and Application 2，2014：381-391.

[12]Nizar A，Houda B M，Said N A.A new sliding function for discrete predictive sliding mode control of time delay systems[J].International Journal of Automation and Computing，2013，10（4）：288-295.

[13]Qudrat K，Aamer I B，Sohail I，et al.Dynamic integral sliding mode for MIMO uncertain nonlinear systems [J].International Journal of Control，Automation，and Systems，2011，9（1）：151-160.

[14]刘燕斌，陆宇平.基于反步法的高超音速飞机纵向逆飞行控制[J].控制与决策，2007，22（3）:313-317.

[15]XU Haojian，Mimirani M D，Joanou P A.Aaptive sliding mode control dsesign for a hypersonic flight vehicle [J].Journal of Guidance Control and Dunamic 2004，27（5）:829-838.

Double power reaching law based sliding mode control for hypersonic vehicle based on disturbance observer

JIANG Ding-guo1，LIU Rong2，YANG Fan1
（1.College of Automation Engineering，NUAA，Nanjing 210016，China；2.Key Laboratory of Advanced Technology for Unmanned Aerial Vehicle UAV Research Institute，NUAA，Nanjing 210016，China）

The intelligence-nonlinear control scheme via double power reaching law based sliding mode control method is proposed to solve the problems of model uncertainties and unknown outside disturbances.Firstly，the aerodynamic parameters of the morphing vehicle are replaced with curve-fitted approximation in order to build the accurate model for the purpose of control design in the hypersonic flight.Then the nonlinear vehicle model is transformed into the strict feedback multi-input/multi-output nonlinear system by using the input-output feedback linearization approach.At the same time，the disturbance observer is used to approximate the unknown disturbance，and the sliding mode method is used to solve the problem of non matching and uncertainty.Finally，according to the buffeting problem in sliding mode control，the double power is improved.Finally，simulation results show that the proposed method can ensure the global stability of the closed-loop system，and has good tracking performance and robust performance

hypersonic vehicle；disturbance observer；double power；sliding mode；buffeting

TN249

A

1674-6236（2017）09-0096-05

2016-07-11稿件编号：201607089

总装预研基金资助项目（51325010601）

姜定国（1990—），男，安徽天长人，硕士研究生。研究方向：控制工程。