基于PageRank的马尔可夫链研究

张 桃，吴小伟

（1河海大学 商学院，江苏 南京210000；2江苏省邮电规划设计院有限公司 江苏南京 210019）

基于PageRank的马尔可夫链研究

张 桃1，吴小伟2

（1河海大学 商学院，江苏 南京210000；2江苏省邮电规划设计院有限公司 江苏南京 210019）

PageRank向量是一个离散时间、有限状态马尔可夫链的稳态分布。同时，马尔可夫链理论已经得到了充分发展，利用马尔可夫链可以更好地理解和分析有关PageRank的问题。本文基于循环或者排名下沉所造成的PageRank收敛问题，通过对马尔可夫链的数学内容进行研究的方法，得出不可约马尔可夫链的暂态行为和极限行为，并对不可约马尔可夫链的特征进行总结。

PageRank；不可约马尔可夫链；极限行为

马尔可夫链理论已经得到了充分发展，而且适用于PageRank问题。利用马尔可夫理论，可以对PageRank向量方程加以修正，以确保得到预期的结果、收敛性质等。幂法的传统终止准则指出，当相邻两次迭代所得结果的差别小于某个预先给定的容许限时，算法停止。但是研究者近期的研究结果表明，迭代应该在幂法所得的PageRank向量近似值的排序达到收敛时停止[1]。实验表明，在某些数据集上，节省的迭代次数加大，有效的提高了运算效率。即使减少了几次迭代数量，考虑到PageRank问题的规模，也是值得肯定利用的[2]。因此，对于任何初始向量，如果其是随机、不可约且非周期性的，则应用马尔可夫矩阵P的幂法将收敛到唯一一个稳态向量的正向量[3-5]。因此，如果将H修改为具有预期结果性质的马尔可夫矩阵，那么由于循环或者排名下沉所造成的PageRank收敛问题便可以得到解决。文中通过对马尔可夫链的数学内容分析，对不可约马尔可夫链的暂态行为和极限行为进行研究分析。

1 PageRank迭代过程中的问题

1.1 排名下沉

利用π（0）T=1/neT开始迭代过程，其中 eT是一个所有元素值均为1的全1行向量。在利用该初始向量执行方程 π（k+1）T=π（k）TH 时，排名下沉问题就会出现，即那些在各次迭代中累计起越来越多的PageRank的页面，它们最终垄断了得分，并拒绝与其他页面分享PageRank。如图1所示，结点4、5和6所形成的团簇将会共同囤积PageRank。对方程π（k+1）T=π（k）TH经过13次迭代后，π（13）T（0 0 0 2/3 1/3 1/5）。同时，随着结点积累了PageRank，某些结点可能会完全无法获得得分。因此，当大多数结点都被赋予了一个值为0的PageRank时，根据PageRank值来进行结点的排名就不仅运算规模大，同时成本较高。

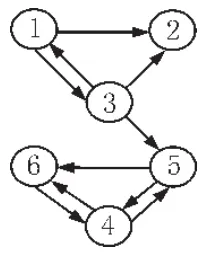
图1 具有6个页面的网络有向图

1.2 循环问题

如图2所示，页面1仅指向页面2，反之亦然，因此就形成一个无限的环路或者循环。假设方程π（k+1）T=π（k）TH 的迭代过程由π（0）T=（1 0）开始，则不论这一过程运行过长时间，迭代都不会收敛。迭代值π（k）T将在两个值之间进行无限次翻转：当k是偶数时，值为（1 0）；当k时奇数时，值为（0 1）。

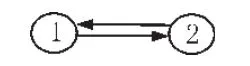
图2 存在循环的简单图

2 不可约马尔可夫链

分析图3可知，当上网者随机选择当前正在浏览页面中的链接时，便可以获取一条马尔可夫链，它由这个链接结构上的随机游走所定义，其转移概率矩阵为不可约随机矩阵H：

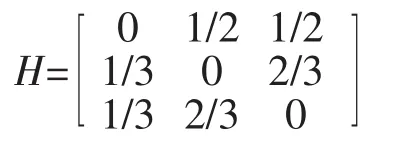
此时，超链接矩阵H是随机的，如果存在一个悬挂节点，则H将具有一个全0行，此时H将不再是随机的，而该过程也不再是一条马尔可夫链。

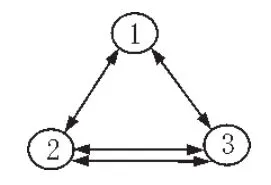
图3 微型的3页面网络

2.1 暂态行为

假设初始分布向量PT（0）=（P1（0）P2（0）...Pn（0）），那么首先需要计算第一次转移后处于任意给定状态的概率，即确定 PT（1）=（p1（1）p2（1）...pn（1）），需要注意，该次计算需要在第二次转移前进行[9]。令∧和∨分别表示逻辑与和逻辑或，那么由此可得，对于每个j，

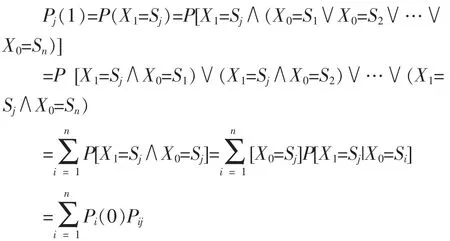
由以上计算可知，PT（1）=PT（0）P描述了由初始分布到一步之后的分布之间的演化过程，根据 “无记忆”的马尔科夫性[10]，进而可得两步之后的情形，即将PT（1）作为初始分布按上述计算方法重聚计算。因此，PT（2）=PT（1）P，PT（3）=PT（2）P，进而可得 PT（k）=PT（0）Pk。若，则PT（k）=PT（0）Pk中可得，对每个i=1，2，...，n，有由此可知，若P是一条定义于状态{S1，S2，…，Sn}上的马尔可夫链的转移概率矩阵，则矩阵Pk表示k步转移概率矩阵，即它的（I，j）元素是由Si经过k步转移到 Si的概率，第k步分布向量由PT（k）=PT（0）Pk得出。

2.2 极限行为

对马尔可夫链的极限性质进行分析，需要将随机矩阵族分为P不可约且存在和P不可约且不存在两种互不相交的类型[11-13]，具体分析如下：

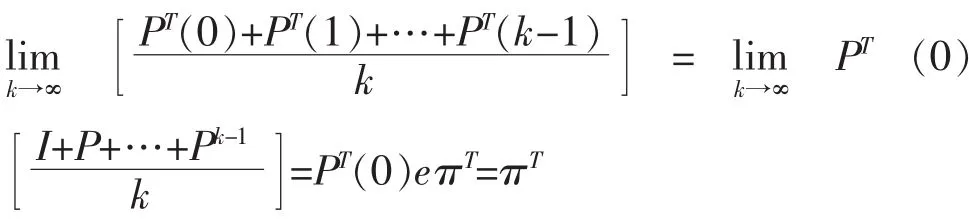
2.3 不可约马尔可夫链的特征总结

令P为状态{S1，S2，…，Sn}上的不可约马尔可夫链的转移概率矩阵，并πTP=πT，‖π‖1=1。因此，对于每个初始分布PT（0），则可知：

1）k步转移矩阵为Pk，第k步分布向量为PT（K）=PT（0）Pk；

3）无论P是素矩阵还是非素矩阵，πT的第j个元素πj都对应了足够长时间内链处于Sj的时间比例，且向量πT是链的唯一的稳态分布向量[14-15]。

3 结 论

马尔可夫链的研究已经展现其有效性，研究方法和思路更加追求创新和效率，但是无论暂态行为或者极限行为，目前的研究都还不尽完善。由于不同算法给出的矩阵彼此之间存在明显差别，因此未来的研究工作可以将多个相互独立的算法的结果加以融合。

[1]Grace E.Cho and Carl D.Meyer.Aggregation/ disaggregation errors for nearly uncoupled Markov chains[C]//Technical report，NCSU Tech.Report. 2013.

[2]李稚楹.PageRank算法研究综述[J].计算机科学，2011（38）:185-188.

[3]荣腾中.高阶马尔可夫链平稳分布的存在唯一性[J].系统工程理论与实践，2013（33）:2016-2019.

[4]肖敬伟.基于PageRank的缓存替换策略[J].信息技术，2016（6）:107-110.

[5]宫秀文.基于PageRank的社交网络影响最大化传播模型与算法研究[J].计算机科学，2013（40）:136-140.

[6]夏双志.目标存在状态变量的非齐次马尔可夫链模型[J].西安电子科技大学学报，2013（40）:49-54.

[7]Carl D.Meyer and James M.Shoaf.Updating finite Markov chains by using techniques of group matrix inversion.Journal of Statistical Computation and Simulation，1980：161-179.

[8]William J.Stewart Numerical experiments with iteration and aggregation for Markov chains.ORSA Journal on Computing，2011，4（3）:336-50.

[9]Cleve B.Moler.Numerical Computing with MATLAB [M].SIAM，2004.

[10]Grace E.Cho and Carl D.Meyer.Aggregation/ disaggregation errors for nearly uncoupled.

[11]William J.Stewart.Introduction to the Numerical Solution of Markov Chains[M].Princeton University Press，2014.

[12]Carl D.Meyer.Stochastic complementation，uncoupling Markov chains and the theory of nearly reducible systems.SIAM Review，1989：240-270.

[13]Grace E.Cho and Carl D.Meyer.Comparison of perturbation bounds for the stationary distribution of a Markov chain[M].Linear Algebra and Its Applications，2010：135-155.

[14]Eugene Seneta.Sensivity analysis，ergodicity coefficients and rank-one updates for finite Markov chains[M].In William J.Stewart，Editor，Numerical Solution of Markov chains，1991：121-130.

[15]Carl D.Meyer.Matrix Analysisand Applied Linear Algebra[M].SIAM.Philadelphia，2000.

The study of Markov chains based on PageRank

ZHANG Tao1，WU Xiao-wei2
（1.Business School of HOHAI University，Nanjing 210000，China；2.Jiangsu Posts& Telecommunication Planning And Designing Institute Co.Ltd，Nanjing 210019，China）

PageRank vector is a discrete-time，finite-state Markov Chains steady state distribution.At the same time，the theory of Markov Chains has been fully developed，with which we can understand and analyze the problem about PageRank.Based on convergence of PageRank resulted from loops or sinking rank，this paper analyzes transient behavior and limited behavior of irreducible Markov Chains and concludes the feature of them with the study of overarching ideas of Markov Chains.

PageRank；irreducible markov chains；limited behavior

TN0

A

1674-6236（2017）09-0036-03

2016-07-11稿件编号：201607090

江苏省社科联研究基金（201035）

张 桃（1992—），女，江苏徐州人，硕士。研究方向：企业管理、市场营销。