Lorenz系统参数估计方法研究

章翠莲，李维德*，朱高峰

(1.兰州大学数学与统计学院, 甘肃 兰州 730000; 2.兰州大学资源环境学院, 甘肃 兰州 730000)

Lorenz系统参数估计方法研究

章翠莲1，李维德1*，朱高峰2

(1.兰州大学数学与统计学院, 甘肃 兰州 730000; 2.兰州大学资源环境学院, 甘肃 兰州 730000)

马尔科夫链蒙特卡洛方法(简称MCMC)可用于复杂系统的不确定性估计和参数估计.基于贝叶斯理论，运用几种改进的MCMC方法：自适应Metropolis 算法(AM)、延迟拒绝自适应Metropolis算法(DRAM)、差分进化马尔科夫链算法(DE-MC)对具有复杂的动态性质的Lorenz 混沌系统未知参数进行了探讨性的估计.根据未知参数的后验概率密度似然函数，利用MATLAB 仿真，选取样本点出现频率高的区间作为目标分布区域，并通过缩小先验分布范围来计算参数的估计值.分析比较这三个算法模拟的结果，得出如下结论：合适的目标分布区域在参数估计中很关键；在搜索样本点上，DRAM 算法的遍历性最高；DE-MC 算法可使Lorenz 系统获得较为精确的参数向量，更适用于复杂系统未知参数的估计.

AM；DRAM；差分进化马尔科夫链；Lorenz 混沌系统；参数估计

1963年，洛伦兹提出了第一个表现奇异吸引子的动力学系统，即Lorenz系统[1].该系统表现出非线性动力学系统的复杂形式——具有混沌动态性质.近年来，混沌系统在保密通信，人工智能以及生命科学等领域得到应用和发展.但由于混沌系统的复杂性，参数的不可观测性，或者保密性，系统的参数是未知的.因此系统的参数估计在混沌控制以及同步领域上的作用是不可估量的[2].

通过观测数据求模型的未知参数，是建模分析中的重要步骤，但由于观测过程中存在系统误差以及观测信息的偶然误差，不一定可求得合适的参数解，或者得出的参数解不唯一，因此本文采用基于贝叶斯理论下改进的MCMC方法对Lorenz系统未知参数估计进行探讨性的研究.

MCMC的Metropolis-Hasting(M-H)算法，其思想是构造一个以目标分布π(x)为不变分布的马尔科夫链,通过一个概率密度函数q(x,y) (称为建议函数)来实现这一分布[3,4]. 该方法是否具有收敛性取决于是否选取合适的建议分布函数.假设当前状态为x，则从建议函数q(x,.)产生一个候选点y，那么接受概率:

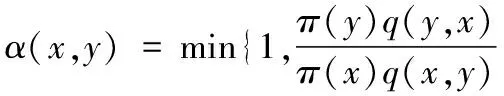
(1)

若α>u(u是[0,1]均匀分布的随机数)，接受候选点y作为新的采样点，否则复制原来的x作为新的采样点.

当建议分布为对称分布时，即q(x,y)=q(y,x).此时接受概率为：

(2)

近年来，许多研究人员在MCMC算法的运行效率和效果做出许多努力从而改进了方法.HeikkiHaario等提出了自适应Metropolis算法，简称AM.这个算法利用了MarkovChain的历史信息自动调节提议函数的协方差矩阵，与随机游走算法相比，提高了算法运行效率[5,6].文献[2] 应用了该算法对Lorenz系统的参数进行了估计.在AM算法提出后，HeikkiHaario等又提出了自适应Metropolis采样和延迟拒绝相结合的算法：延迟拒绝自适应Metropolis算法，简称DRAM.这个算法提高了马尔科夫链的遍历性和采样点的接受率[7].TerBraak则通过遗传算法思想，提出了一种差分进化马尔科夫链算法，简称DE-MC.该算法多条链同时运行，其解决了MCMC的一个重要问题，即为跳跃分布提供了合适的范围和方向[8].基于贝叶斯理论，本文主要将这三种改进的MCMC算法运用到对Lorenz系统的未知参数估计，对这三种方法进行探讨性的讨论，得出解决Lorenz系统未知参数估计的较优方法.

1 理论与算法

1.1 贝叶斯理论

贝叶斯方法提供了一个涵盖模型不确定性的框架，在这个框架下，具有概率分布的贝叶斯方法的关键的特点在于描述了参数和模型的不确定性[9].

基于贝叶斯理论，我们认为未知参数向量(对Lorenz系统而言，其有3个未知参数，因此d=3),在对X进行初步推断时，根据相关未知参数的信息 ，我们认为其先验分布为p(θ).在对系统进行观测采样后，得到观测信息(包含N个样本点).因此，由贝叶斯估计，系统参数的后验分布，观测信息和先验分布之间的关系[2]：

(3)

考虑到Z是已知的信息，上式可以写成：

p(θ|Z)∝p(Z|θ)P(θ)

(4)

我们知道，贝叶斯推断的核心在于使用似然函数去分析参数的不确定性.因此对p(Z|), 在实际中一般用似然函数表示，其值越大表明拟合程度越好[10].

1.2AM算法

AM是基于Metropolis算法中的随机游走算法(RWM)[11]改进而来的,该算法关键在于，先构造具有高斯分布的建议函数，利用马尔科夫链先前全部样本信息计算建议分布的协方差矩阵，自适应地向目标函数逼近[12]. 利用该点，通过后验分布获得的信息使得建议分布得到更新.在第i步中，Haario等提出了以当前点作为均值和具有协方差矩阵Ci的多元正态分布.该协方差Ci的定义为：

(5)

其中，sd是缩放因子，a1>0 是一个很小的数，它们分别取为2.382/d与10-6.在理论上要保证Ci非奇异，Id是d维单位矩阵.C0是初始协方差矩阵.Cov(θ0,...,θi-1)表示θ0,...,θi-1的协方差矩阵. 若初始协方差过大也会使AM算法自适应性变差；反之，初始协方差过小降低AM算法的遍历性. 为非自适应长度，其值越大自适应性越慢[12].

AM算法流程如下：

a)设定i=1，对所求的参数变量初始化；

b)利用(5)式计算协方差矩阵Ci；

c)产生候选点θ*～N(θi-1,Ci)；

d)根据(1)式，计算接受概率α=min{1,p(θ*|Z)/p(θi-1|Z)}；

e)产生满足均匀分布的随机数u～U[0,1]；

f)若α>u,则θi=θ*，否则θi=θi-1；

g)重复b)～f)，直到完成产生指定的迭代数量的样本.

1.3DRAM算法

DRAM是基于延迟拒绝算法[13]和AM算法相结合而得来的算法[7].

DR算法是具有不同提议函数和转移核的MCMC方法.Peskun和Tierney已证明出有限维的状态空间和普遍的状态空间里DR算法通过降低停留在当前候选点的概率提高MCMC方法的运行效率[14,15].其主要思想在于：在进行M-H抽样时，若当前的候选点被拒绝，不是保持当前状态不变，而是从当前位置利用改变的提议函数再次移动，通过对第2次移动的候选点的接受概率计算来保持马尔科夫链的可逆性，其本质上是通过对提议函数局部自适应调整来提高算法的效率[12].

在算法进程中，假定当前位置为x，用π(·)表示该点的目标分布函数，根据多元正态分布函数q0(x,·)产生新的候选点y，接受率(类似式(1))为：

(6)

若在点x被拒绝，则根据当前位置和被拒的候选点再次移动，从新的建议函数q1(x,y,·)产生新的候选点z,相应的接受概率为[16]：

(7)

若是第二级的候选点仍被拒绝，则可在被拒的候选点z上再进行第三级移动.

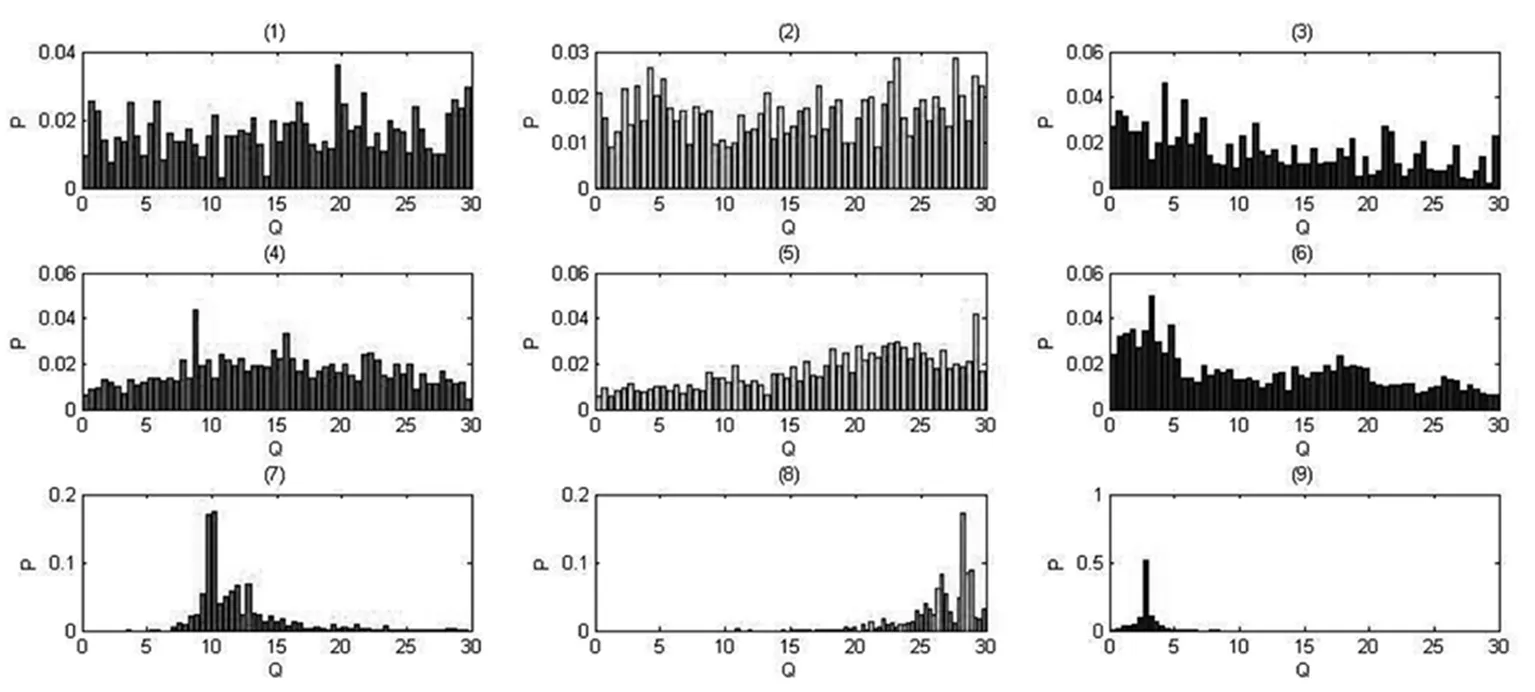
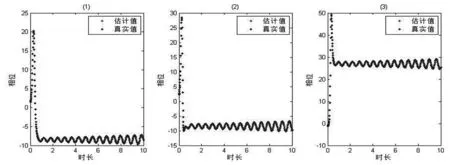
DRAM与AM算法的流程大致相同，不同于AM算法的是在第f)步.将第f)步改动:若α>u, 则θi=θ*，再返回到第b)步继续迭代；若α

1.4DE-MC算法

差分进化马尔科夫链是在具有MCMC模拟的实参数空间上利用Metropolis准则与差分进化算法[17]结合而得来的MCMC算法[8].该算法克服了MCMC方法中建议分布需要选取合适的范围和方向以及相应的计算效率问题.该算法有两个参数：缩放因子γ和平行链的数目N可根据实际情况定义[18].

DE-MC算法的基本过程[8]：

θ*=θi+γ(θa-θb)+ε

(8)

其中，θ*是建议选取的参数集，θi是当前的参数集，θa,θb是从θi不含外的参数集随机选取出来的，γ为缩放因子.ε～N(0,b)d,在这里b很小.建议的参数集接受或者拒绝取决于Metropolis比率,具体可参考(1) 式[16].

上面所列举的三种MCMC方法，AM和DRAM算法都具有自适应性，DE-MC是遗传算法和传统的Metropolis方法相结合的算法.每一种算法各有其相关的优势，因此下面将这三种算法运用到Lorenz模型进行未知参数的估计，进行探讨性的讨论.

2 Lorenz混沌系统参数估计分析

Lorenz系统可由如下的常微分方程组表示：

(9)

我们知道当系统(9)中a,b,r分别为10,28,8/3时，系统表现为混沌现象.Lorenz描述的非线性耗散系统具有初始条件敏感性.在用数值解法求解非线性微分问题时，数值积分方法和编程现实中的误差累积导致模拟的轨道与原来的轨道偏离.即不同的初始条件，不同的算法和编程细节，使得计算轨道是不可重复的.因此，系统的长期行为是不可预测的.本文选取的时间长度为10s.首先对该系统进行数据采样：先让Lorenz系统进行演化,以混沌系统中某一点(1.500，2.230，-1.270)作为初始点，并记为：(x1(0),x2(0),x3(0)).设置时间步长h为0.01s,采用四阶定步长Runge-Kutta算法来求解常微分方程，得出离散的数值解，我们得到Lorenz系统在10s内的1000组离散数据： (x1(ti),x2(ti),x3(ti))(i=0,1,...,1000).

它们可作为观测数据集Z, 由于这些数据在操作过程中必有观测误差，因此可多模拟几次，取每个步长状态的平均值作为观测数据集来减少误差的干扰.

现在已知观测数据集，分别采用AM,DRAM和DE-MC估计出Lorenz系统的未知参数集θ=(a,b,r).由贝叶斯公式求出参数的联合后验概率密度函数.令模型的初始状态量为：(x1(0),x2(0),x3(0))，每隔10个步长共取10个样本点，即抽取0h，10h，...，90h时刻的状态量(x1(ti),x2(ti),x3(ti))(i=1,2,...,10)作为这次的观测数据集Z.

根据贝叶斯公式(3),未知参数的后验分布：

p(a,b,r|Z)=k·p(Z|a,b,r)p(a,b,r)

(10)

其中，k是一个大于0的常数.

在贝叶斯推断中，首先设定未知参数的先验分布p(a,b,r).假设这三个参数均满足独立均匀分布，用U(a),U(b),U(r)分别表示三个参数的均匀分布，则

p(a,b,r)=U(a)U(b)U(r)

(11)

相比较其他分布，均匀分布是最简单的分布，其限定了参数变化的界限，先验分布的界限很小时，目标区域则相对变小，这样有利于提高参数的精确度.通常情况下熟知历史经验更能得到精确的先验分布.

对于式(10)中的p(Z|a,b,r),前面提到观测集是经过多次测量取平均值而得到的.根据普适似然不确定性分析方法GLUE的基本原理,用似然函数来比较模拟值和实测值的拟合程度，本文选用基于残差和的似然函数[19,20]：

(12)

本文取n=10,d=3,M=1.对向量进行更新后，通过用四阶定步长Runge-Kutta算法解Lorenz系统微分方程，时间和步长不变，每隔10h取一个数据，则得到10个数据.第i个数据记为:(y1(ti),y2(ti),y3(ti))(i=1,2,...,10).

由(10)-(12)可得，该系统未知参数的后验概率密度似然函数为：

(13)

在模拟之前，本文先假设三个参数的目标分布区间均为[0,30],即a,b,r的联合先验分布均为：

(14)

后验概率密度似然函数确定后，则可以用AM,DRAM,DE-MC算法对这三个未知参数进行随机抽样.对于AM和DRAM算法,非自适应段长度=200.DRAM算法中，λ=0.1，m=3.

3 仿真结果及分析

考虑到三个参数的目标分布都较大，迭代次数先取为2000，参数初始值则取相对应目标分布中的随机值. 在每个算法进行抽样时，每次都对未知参数向量进行更新，通过计算该随机参数向量的似然后验密度函数值与上一步后验密度函数值的比值，决定是否将该向量作为下一步的值并进行更新.

在各参数的目标分布区间皆为[0,30]时，各个算法模拟出来各参数的马尔科夫链还未收敛(图1)，仿真的结果不理想.根据图1中基于残差平方和似然函数值较大的部分对应的参数向量，即a=9.9529,b=28.2056,r=2.7923时，式(12)中的较大，说明我们估计的参数向量在这个向量的附近.但由于MCMC算法具有随机性，三种算法模拟出来三个参数的直方图都不理想(图2)， 缩小各个参数的目标分布区域再进行Matlab模拟可期望得出更精确的参数向量.重新设置参数的目标分布：a～U[9.9529-2,9.9529+2],b～U[28.2056-2,30],r～U[2.7923-2，2.7923+2]，其他条件不变.

图1 目标分布区间为[0,30]下各算法仿真结果

注：T表示迭代次数，Q表示目标分布区域，L表示基于残差和的似然函数值；(1)-(3)分别是用AM模拟得的参数a,b,r的马尔科夫链；(5)-(7)分别是用$DRAM$模拟得的参数a,b,r的马尔科夫链；(9)-(11)分别是用DE-MC模拟得参数a,b,r的马尔科夫链；(4),(8),(12)分别是用AM,DRAM,DE-MC模拟得到的基于残差和的似然函数值演化过程.

图2 目标分布区间为[0,30]下各算法仿真的参数值方图

注：P表示频率；(1)-(3)分别是用AM模拟出来参数a,b,r的直方图；(4)-(6)分别是用DRAM模拟出来参数a,b,r的直方图；(7)-(9)分别是用DE-MC模拟出来参数a,b,r的直方图.

图3 第一次调整目标分布后各算法仿真结果

在新的参数目标分布区域下，由三个算法模拟出各参数的马尔科夫链以及计算出式(12)的值的演化过程(图3)，我们可以看出DE-MC算法模拟出来的参数r的马尔科夫链已收敛，其他两个参数在小范围里波动，其基于残差的平方和的似然函数值大体比其他两个算法的大.在迭代次数1700-1800范围内，式(12)的值最大，此时参数向量为(9.9875,28.1047,2.6508)，AM和DRAM算法模拟各参数的马尔科夫链皆无收敛的趋势.从遍历性来看，DRAM的遍历性最好(候选点接受率约为0.5)，AM算法次之(候选点接受率约为0.35)，DE-MC的遍历性最差.结合三个算法模拟出各个参数的直方图(图4)，无法从AM算法模拟出样本点的直方图减小目标分布区域；DRAM算法模拟出来的各参数样本点直方图类似正态分布，参数r的最为明显；从DE-MC算法模拟出的各参数样本点直方图可以看出样本点皆分布集中，因此可根据其缩小目标分布区域.考虑DE-MC算法中的式(12)似然函数较大值所对应的参数向量，可将参数向量的目标分布设置为：(9.9875±0.5,28.1047±0.5,2.6508 ±0.2).

图4 第一次目标分布调整后各算法仿真的参数值方图

利用调整后的目标分布区域得出三个算法模拟出来的各参数的马尔科夫链以及由式(12)得到的似然函数值演化图(图5).从图5可看出，DRAM算法与其他两个算法相比，其遍历性最高，样本点的接受概率约为0.54,AM算法样本点的接受概率越为0.14，但是这两个算法最后未收敛.从后验概率密度似然函数来看，DE-MC算法收敛，并且其似然函数值最大.选取似然函数值最大的部分，即用DE-MC算法模拟出的马尔科夫链收敛的那部分，其对应的参数向量约为：(9.9949, 28.0042, 2.6673), 即约为9.9949，约为28.0042，约为2.6673. 将其带入(9)式，经过数值模拟，由(12)式可得出 约为1006，即其与观测集的残差平方和约为0.001. 由此可见，DE-MC算法更适用于Lorenz混沌系统的未知参数估计.

图5 第二次目标分布调整后各算法仿真结果

图6 状态变量估计值与真实值在15-25s内的轨迹对比图

Matlab中解一阶微分方程组初值问题常见的方法为ode45函数，该函数实现了变步长四阶五级的Runge-Kutta-Felhberg算法，采用变步长算法解微分方程[21].将原来的参数向量和通过DE-MC算法求解出来的参数向量代入Lorenz模型的状态方程(9)，利用MATLAB中ode45函数数值解法求解.当时间长度为10s，初始状态相同，发现各状态变量真实值和估计值在10s内的振幅以及频率相似，相位大体相同，轨迹几乎一模一样.其他条件不变，延长时间长度，各状态变量真实值和估计值在20s后开始不在一条轨道上，估计值渐渐脱离原来的轨道(图6).因此，Lorenz系统的长期行为是不可预测的.在选取观测样本数据时，系统不宜长时间演化，时间一般不超过10s. 在适当的目标分布区域内，DE-MC算法适用于短时间演化的复杂系统的参数估计，其最后模拟出的参数向量是有意义的.

4 结论与讨论

本文基于贝叶斯理论的框架，利用MCMC方法中的AM,DRAM和DE-MC算法对Lorenz模型未知参数向量进行采样，经过两次目标分布区域的调整，分析比较各参数的马尔科夫链，得到了系统的参数估计值.本文研究的主要结论总结如下：

(1)当未知参数的目标分布区域较大时，这三个算法模拟出各参数的马尔科夫链皆不收敛，基于残差和的似然函数值不高，效果不是很理想.参照各算法模拟出的似然函数值演化过程图以及各参数样本点的直方图，选取样本点出现频率高的区间作为新的目标分布区域，及时调整先验分布.参数的先验分布越准确，即目标分布区域越小，模拟出来的参数向量越精确.

(2)本文应用了MCMC的三种算法对Lorenz混沌模型未知参数进行了估计.与文献[2]仿真的结果不同的是，从运行过程来看，在相同的迭代次数下，AM算法运行的时间最少；由于DE-MC算法是多条链同时运行，模拟过程最缓慢.从样本点的搜索区域来看，DRAM算法搜索范围大，遍历性最好；而DE-MC算法的遍历性较差.从模拟出来的结果来看，经过两次目标分布区域的调整，在三种算法中，DE-MC算法模拟出的马尔科夫链收敛，并且基于残差和的似然函数值较大，说明模拟出来的参数向量与真实的参数向量相差甚小.

(3)从参数估计的效果看，在适当的目标分布区域内，对于短时间演化的Lorenz混沌系统，DE-MC算法能较快地模拟出该参数向量.对一般的非线性以及动态的模型，DE-MC算法同样能估计模型的参数.

综上所述，AM,DRAM和DE-MC算法皆是通过构造马尔科夫链进行随机模拟，在对Lorenz混沌系统进行未知参数估计的过程中，实际就是在先验分布界定的目标区域对参数向量进行随机且较好抽取样本点的过程，也就是构造马尔科夫链的过程.通过Matlab仿真模拟，DE-MC算法能较好地对Lorenz混沌系统未知参数进行估计，因此该算法能更好地应用在复杂系统的参数估计上.

[1]刘福才, 梁晓明,Hénon. 混沌系统的广义预测控制与同步快速算法[J].物理学报,2005, (10):4584-4589.

[2]曹小群,宋君强.基于MCMC方法的Lorenz混沌系统的参数估计[J].国防科技大学学报,2010,(2):68-72.

[3]ChristropheA,NandoDF.AnintroductiontoMCMCformachinelearning[J].MachineLearning,2003,50,5-43.

[4]陈平，徐若曦.Metropolis-Hastings自适应算法及其应用[J].系统工程理论与实践,2008，(1):100-108.

[5]HaarioH,SaksmanE,TamminenJ.AnadaptiveMetropolisalgoritnm[J].Bernoulli,2001,(2):223-242.

[6]SaksmanE,ViholaM.OntheergodicityoftheadaptiveMetropolisalgorithmonunboundeddomain[J].TheAnnalsofAppliedProbability,2010,(6):2178-2203.

[7]HaarioH,LaineM,MiraA,etal.DRAM:EfficientadaptiveMCMC[J].Statistics&Computing, 2006,(4):339-354.

[8]BraakCJ.AMarkovChainMonteCarloversionofthegeneticalgorithmdifferentialevolution:EasyBayesiancomputingforrealparameterspaces[J].Statistics&Computing, 2006, (16):239-249.

[9]LombardiMJ.Bayesianinferenceforstableditributions:ArandomwalkMCMCapproach[J].ComputationalStatistics&DataAnalysis,2007,(5):2688-2700.

[10]MarshallL,NottD,SharmaA.AcomparativestudyofMarkovchainMonteCarlomethodsforconceptualrainfall-runoffmodeling[J].WaterResourcesResearch, 2004, (40):183-188.

[11]KuczeraG,ParentE.MonteCarloassessmentofparameteruncertaintyinconceptualcatchmentmodels:TheMetropolisalgorithm[J].JournalofHydrology, 1998, (1-4):69-85.

[12]郝燕玲,单志明.基于DRAM算法的α稳定分布参数估计[J].华中科技大学学报，2011,(10):73-78.

[13]TierneyL,MiraA.SomeadaptiveMonteCarlomethodsforBayesianinference[J].StatisticsinMedicine, 1998, (17-18):2507-2515.

[14]PeskunPH.OptimumMonte-CarlosamplingusingMarkovchains[J].BiometrikaTrust, 1973,(3):607-612.

[15]TierneyL.AnoteonMetropolis-Hastingskernelsforgeneralstatespaces[J].AnnalsofAppliedProbability,1998, (1):1-9.

[16]SmithTJ,MarshallLA.Bayesianmethodsinhydrologicmodeling:AstudyofrecentadvancementsinMarkovchainMonteCarlotechniques[J].WaterResourcesResearch, 2008, (12):67-76.

[17]StornR,PriceK.Differentialevolution-Asimpleandefficientheuristicforglobaloptimizationovercontinuousspaces[J].JournalofGlobalOptimization, 1997,(4):341-359.

[18]BraakCJFT,VrugtJA.DifferentialevolutionMarkovchainwithsnookerupdaterandfewerchains[J].Statistics&Computing, 2008,(4):435-446.

[19]BevenKJBinleyAM.Thefutureofdistributedmodels:Modelscalibrationanduncertaintyprediction[J].HydrologicProcess,1992,(2):279-298.

[20]FreerJK,BevenKJ.Bayesianestimationofuncertaintyinrunoffpredictionandthevalueofdata:AnapplicationoftheGLUEapproach[J].WaterResourcesResearch,1996,(7):2161-2173.

[21]薛定宇,陈阳泉.高等应用数学问题的MATLAB求解(第3版)[M].北京：清华大学出版社，2013.

(责任编校：晴川)

Study on Methods of Parameters Estimation of Lorenz System

ZHANG Cuilian1,LI Weide1*, ZHU Gaofeng2

(1.School of Mathematics and Statistics, Lanzhou University, Lanzhou Gansu 730000, China; 2. School of Resources and Environment, Lanzhou University, Lanzhou Gansu 730000, China)

Markov Chain Monte Carlo method (in short as MCMC) is useful to the uncertainty and parameter estimation for complicated system. Based on the Bayesian theory, the paper proposes an explorative study by utilizing several MCMC methods, such as Adaptive Metropolis (AM), Delay Rejection Adaptive Metropolis (DRAM) and Differential Evolution Markov Chain (DE-MC) algorithm, to estimate the parameters of Lorenz system which has complicated dynamical property. According to the posterior probability density likelihood function of unknown parameter, utilizing MATLAB simulation, selecting the region where sampling points appearing with high frequency as target distribution area, and narrowing the scope of the prior distribution, we calculate the estimation value of parameters. By analyzing and comparing the simulated results of the three algorithms mentioned above, we achieved these conclusions: suitable target distribution area is critical to estimate parameter; DRAM algorithm has high ergodicity in searching sampling points; DE-MC algorithm is more appropriate for complicated system with unknown parameter estimation, which makes Lorenz system obtain precise parameter vector.

AM; DRAM; differential evolution Markov Chain; Lorenz chaotic system; parameter estimation

2016-10-14

国家自然科学基金(批准号：41571016)资助项目.

章翠莲(1991— )，女，广西钦州人，兰州大学数学与统计学院硕士生.研究方向：应用数学.

O212.1

A

1008-4681(2017)02-0005-06

*通讯作者：李维德(1967— )，男，甘肃兰州人，兰州大学教学与统计学院教授，博士.研究方向：数字生态学.