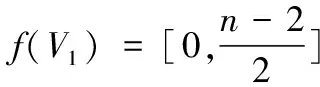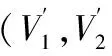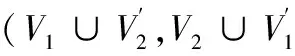连路树的全优美性

张明军

(兰州财经大学信息工程学院, 甘肃 兰州 730020)

连路树的全优美性

张明军

(兰州财经大学信息工程学院, 甘肃 兰州 730020)

图的标号理论是研究计算机网络节点的技术手段之一.给出了优美树、二分优美树、边对称树以及全优美标号的概念，定义了一类连路树T，并证明了连路树T及其边对称树是全优美标号、全优美图.为计算机网络的发展提供参考.

二分优美树；优美标号；全优美标号；边对称树

1 准备知识

图的标号理论是研究计算机网络节点的技术手段之一.优美图是图的标号研究中十分重要的课题之一.优美图在物流运输、编码理论、天文学等领域均有应用.图的标号问题来自数学和图论学科自身的问题, 甚至是编码、晶体学中X-射线的二分性、通信网络设计中的寻址、最佳电路布局和射电天文等应用领域[1,2]. 在优美树猜想的研究中, 新的标号以及新的问题不断涌现[3]. 本文讨论了连路树T及其边对称树是全优美标号、全优美图.

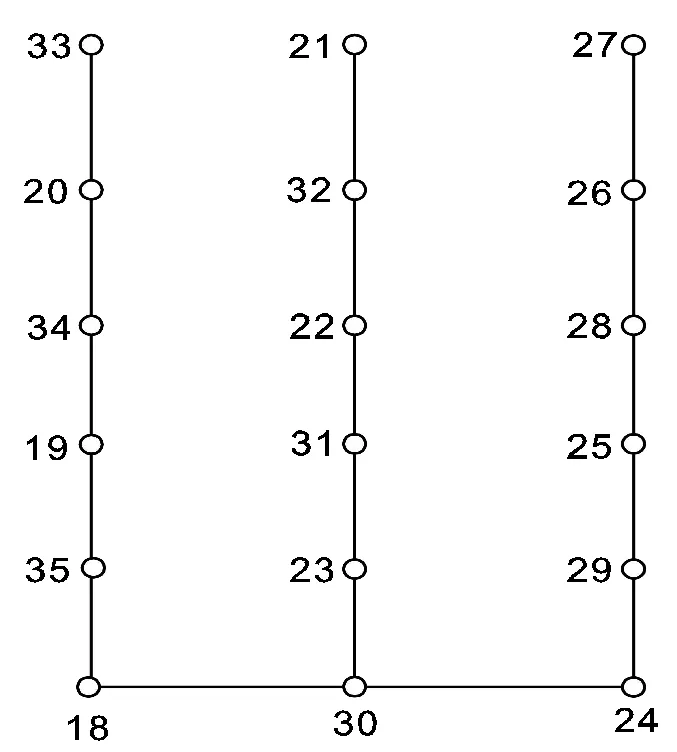
本文涉及的图均为有限、无向、简单图. 文中没有定义的术语和符号均采用文献[3]. 本文中用记号[m,n]表示非负整数集{m,m+1,m+2,…,n}, 其中m和n均为整数; [k,l]e表示偶数集{k,k+2,k+4,…,l}, 其中k和l都是偶数, 且满足0≤k

定义1[3,4].如果一棵n个顶点的树T有一个正常标号f:V(T)→[0,n-1], 使得边标号集合f(E(T))={f(uv)|uv∈E(T)}=[1,n-1], 则称T为优美树,f是T的一个优美标号.

定义2[5].设 (V1,V2) 是树T的顶点集的二部划分, 如果T有一个优美标号f, 使对树T任意 2 个顶点x∈V1和y∈V, 总有f(x)

定义3[6].对于一个(p,q)-图G, 如果存在一个双射f:V(G)∪E(G)→[1,p+q], 使得边标号集合f(uv)|uv∈E(G)=[1,q], 其中边标号为f(uv)=|f(u)-f(v)|,则称G为全优美图(STGG), 并称f为G的一个全优美标号 (STGL).

定义4[7].设T是一棵n阶树,T′ 是T的一个拷贝, 用一条边e=xx′将T中的点与其拷贝的同构点相连, 得到的新树称为树T的边对称树.

设有s条路Pi=ai,0ai,1,…,ai,2m+1(i=1,2,…,s), 用边连接顶点对ai,0和ai+1,0(i=1,2,…,s-1), 所得到的树称为连路树(path-linkedtree), 记为T, 其中ai,j是路Pi上的顶点,V(Pi)={ai,j∣j∈[0,2m+1]}, 顶点ai,0,ai+1,0(i=1,2,…,s-1)以及连接他们的边构成路树T的主路, 即是Q=a1,0a2,0…as,0. 图1给出一棵连路树T.

2 主要结果及证明

定理1. 连路树T有全优美标号, 是全优美图.

证明 连路树T有n=s(2m+1)个顶点. 下面给出树T的标号函数f:

记V1={ai,j∣(i,j)≡(1,0)(mod2)}∪{ai,j∣(i,j)≡(0,1)(mod2)},

V2={ai,j∣(i,j)≡(1,1)(mod2)}∪{ai,j∣(i,j)≡(0,0)(mod2)}.

fmax(ai,j)=s(m+1)-m-2,i≡1(mod2),j≡0(mod2);

fmax(ai,j)=s(m+1)-1,i≡0(mod2),j≡1(mod2).

即fmax(V1)=s(m+1)-1. 同理能够得到

fmin(ai,j)=s(m+1),i≡1(mod2),j≡1(mod2);

fmin(ai,j)=s(m+1)+m+1,i≡0(mod2),j≡0(mod2).

即fmin(V2)=s(m+1). 当s为偶数时, 有fmax(V1)

下面证明f是优美标号.

(2) 证明所有边标号中没有标号相同的边标号. 在E(T)中任取 2 条边e1=u1u2,e2=v1v2,下面分 4 种情况讨论.

情形I: 主路上的边标号与路Ps上的边标号不相同.

主路上的边标号为:f(e1)=|f(ai,0)-f(ai+1,0)|=|n-2(m+1)i|.

路Ps上的边标号为:

f(e2)=|f(ai,j)-f(ai,j+1)|=|2m+n-2(m+1)i-j+1|,i≡1(mod2),j∈[0,2m]

f(e2)=|f(ai,j)-f(ai,j+1)|=|n-2(m+1)i+j+1|,i≡0(mod2),j∈[0,2m]

当i≡1(mod2) 时, 若f(e1)=f(e2), 则一定有2m-j+1=0, 此时j=2m+1, 与j∈[0,2m]矛盾. 因此,f(e1)≠f(e2). 因为j+1≠0, 所以f(e1)≠f(e2) (i≡0(mod2)). 故主路上的边标号与路Ps上的边标号都不相同.

情形II: 主路Ps上的边标号互不相同. 由于

f(e1)=|f(ap,0)-f(ap+1,0)|=|n-2p(m+1)|;

f(e2)=|f(aq,0)-f(aq+1,0)|=|n-2q(m+1)|.

其中p,q∈[1,s-1],p≠q

所以,f(e1)-f(e2)=2|(m+1)(p-q)|≠0(p≠q),即主路上的边标号互不相同.

情形III: 同一条路Ps上的边标号互不相同. 若i≡1(mod2), 得

f(e1)=|f(ai,k)-f(ai,k+1)|=|2m+n-2(m+1)i-k+1|;

f(e2)=|f(ai,l)-f(ai,l+1)|=|2m+n-2(m+1)i-l+1|.

其中k,l∈[0,2m],k≠l.

因为k≠l, 显然有f(e1)≠f(e2). 若i≡0(mod2), 有

f(e1)=|f(ai,k)-f(ai,k+1)|=|n-2(m+1)i+k+1|;

f(e2)=|f(ai,l)-f(ai,l+1)|=|n-2(m+1)i+l+1|.

其中k,l∈[0,2m],k≠l.

注意到k≠l, 故f(e1)-f(e2)=|k-l|≠0. 可断言, 路Ps上的边标号互不相同.

情形IV: 不同的路Pi1和Pi2(i1≠i2,i1,i2∈s) 上的边标号互不相同.

(i) 若i1,i2≡1(mod2), 则有

f(e1)=|f(ai1,k)-f(ai1,k+1)|=|2m+n-2(m+1)i1-k+1|;

f(e2)=|f(ai2,l)-f(ai2,l+1)|=|2m+n-2(m+1)i2-l+1|.

其中k,l∈[0,2m].

假设f(e1)=f(e2), 即就是 2(m+1)i1+k=2(m+1)i2+l, 从而有2(m+1)(i1-i2)=l-k.

这里l-k∈[-2m,2m], 显然矛盾,f(e1)≠f(e2)成立.

(ii) 若i1,i2≡0(mod2), 因有

f(e1)=|f(ai1,k)-f(ai1,k+1)|=|n-2(m+1)i1+k+1|;

f(e2)=|f(ai2,l)-f(ai2,l+1)|=|n-2(m+1)i2+l+1|.

其中k,l∈[0,2m].

与 (i) 中证明类似, 同理可得f(e1)≠f(e2).

(iii) 当i1≡1(mod2) 和i2≡0(mod2) 时, 有

f(e1)=|f(ai1,k)-f(ai1,k+1)|=|2m+n-2(m+1)i1-k+1|;

f(e2)=|f(ai2,l)-f(ai2,l+1)|=|n-2(m+1)i2+l+1|.

其中k,l∈[0,2m].

假定f(e1)=f(e2), 就有 2m-2(m+1)i1-k=-2(m+1)i2+l, 也就是2(m+1)(i1-i2) +k+l=2m. 如果i1>i2, 则有 (i1-i2)min=1. 但是, 2(m+1)(i1-i2)+k+l=2m+2+k+l>2m矛盾. 如果i1

综上所述, 所有边标号中没有相同的边标号.即f(E(T))=[1,n-1].又fmax(V1)

因此, 连路树T是二分优美树.

(3)下面证明连路树T有全优美标号, 是全优美图.

连路树T有n个顶点和n-1 条边的二分优美树, (V1,V2) 是它的顶点集的二部划分,f是T的一个集有序优美标号. 给出连路树T的一个新标号：h(ai,j)=n+f(ai,j). 则f(E(T))=[1,n-1],.f(V(T))=[n,2n-1]，E(T)∪V(T)=[1,2n-1]=[1,p+q] (p,q分别表示连路树T的顶点数和边数).又f(E(T))=[1,n-1], 所以, 连路树T有全优美标号, 是全优美图(STGG).

图2、图3是解释定理 1 的一个例子.

图2 18个顶点连路树的全优美标号

图3 32个顶点连路树的全优美标号

定理2.连路树T的边对称树是全优美标号, 全优美图.

下面证明连路树T的边对称树H有全优美标号, 是全优美图.

由上述证明可知连路树T的边对称树H是一个有2n个顶点和 2n-1条边的二分优美树.h是边对称树H的一个集有序优美标号. 下面给出边对称树H的一个新标号：g(ai,j)=2n+h(ai,j). 由定理可知,f(E(T))=[1,2n-1],f(V(T))=[2n,4n-1].

图4和图5是解释定理 2 的例子.

图4 18个顶点连路树的边对称树的全优美标号

图5 32个顶点连路树的边对称树的全优美标号

由定理 2 的证明可得到下面的推论：

[1]BloomGS,GolombSW.Applicationsofnumberedgraphs[J].ProceedingsoftheIEEE, 1997, (4): 562-570.

[2]GallianJA.Adynamicsurveyofgraphlabeling[J].TheElectronicJournalofCombinatorics, 2009, 12: 42-43.

[3]BondyJA,MurtyUSR.GraphTheorywithApplications[M].London:TheMacmillanPressLtd, 1976.

[4]PereiraJ,SinghT,ArumugamS.On(k,d)-Skolemgracefulgraphs[J].ElectronicNotesinDiscreteMathematics,2015,48:81-88.

[5]YaoB,ChengH,YaoM.Anoteonstronglygracefultrees[J].ArsCombinatoria, 2009, (92) :155-169.

[6]SubbiahSP,PandimadeviJ,ChithraR.Supertotalgracefulgraphs[J].ElectronicNotesinDiscreteMathematics,2015,48:301-304.

[7]ZhouX,YaoB,ChenX.Discussodd-gracefultreesconjecture[J].JournalofShandongUniversity(NaturalScience), 2012, (12): 31-36.

(责任编校：晴川)

Super Total Gracefulness on Path-linked Trees

ZHANG Mingjun

(School of Information Engineering, Lanzhou University of Finance and Economics,Lanzhou Gansu 730020, China)

The labeling theory of graphs is one of the technical means to study the nodes of computer networks. We present the concepts of trees including graceful tree, bipartite graceful tree, edge symmetric trees and super total graceful labelling. We define a class of path-linked tree T and prove that every path-linked tree T and its edge symmetric tree are super total graceful graph, so as to provide a reference for the development of computer networks.

bipartite graceful tree; graceful labelling; super total graceful labelling; edge symmetric tree

2017-01-31

国家自然科学基金(批准号：61662066、61363060)资助项目.

张明军(1973— ), 男, 山东青州人, 兰州财经大学信息工程学院副教授, 硕士.研究方向：图的标号及复杂网络.

O

A

1008-4681(2017)02-0001-04