基于地球椭球的真三维井眼定位方法
2017-05-12刘修善中国石化石油工程技术研究院北京100101
刘修善(中国石化石油工程技术研究院,北京100101)
基于地球椭球的真三维井眼定位方法
刘修善
(中国石化石油工程技术研究院,北京100101)
针对现行井眼定位方法存在的问题,提出真三维井眼定位方法,并进行算例分析。现行定位方法以网格北作为指北基准,基于地图投影坐标进行水平面定位,基于高程坐标进行垂向定位,且二者相互独立,只使用一点处的子午线收敛角和磁偏角来归算全井的井眼轨迹,存在固有缺陷和误差。基于地球椭球及其解算原理,揭示了井口坐标系与大地坐标系及高程坐标系之间的转换关系,提出了采用真北作为指北基准的真三维井眼定位方法。算例分析结果表明,现行定位方法算得的靶点垂深偏小、水平位移偏大,与真三维定位方法相比存在较大误差。真三维井眼定位方法从根本上解决了现行定位方法存在的问题,能精准定位靶点与井口间的相对位置,可显著提高井眼轨迹设计的精确性和可靠性。图3表6参16
钻井理论;定向钻井;井眼轨迹;井眼定位
引用:刘修善. 基于地球椭球的真三维井眼定位方法[J]. 石油勘探与开发, 2017, 44(2): 275-280.
LIU Xiushan. A true three-dimensional wellbore positioning method based on the earth ellipsoid[J]. Petroleum Exploration and Development, 2017, 44(2): 275-280.
0 引言
井眼轨迹设计、监测与控制是定向钻井的核心技术。在设计井眼轨迹时,首先应确定井口和靶点的位置,然后求得靶点相对于井口的垂深、水平位移等参数[1-3]。在井眼轨迹监测和控制过程中,也需要随时确定井眼轨迹的空间坐标,以保证钻达预期目标。这些都属于井眼定位问题。
为满足井眼轨迹设计、监测与控制的需要,钻井工程师常以井口为原点,以正北、正东及垂直方向为坐标轴,建立一个三维笛卡尔坐标系,称为井口坐标系。目前,国内外都采用水平面定位和垂向定位相结合的方法进行井眼定位。在井口坐标系下,靶点北坐标和东坐标分别为靶点与井口之间的地图投影纵坐标之差和横坐标之差,而靶点垂深为井口与靶点的高程之差[1-3]。
然而,现行井眼定位方法存在一些明显缺陷。例如,将地球椭球面投影到平面上存在投影变形,致使地图投影坐标不可避免地会产生误差;水平面定位与垂向定位互不相关,不同直井在垂直方向上永远平行,但事实上它们应越来越靠近并在地心附近相交。
目前,井眼定位的研究热点主要集中于井眼轨迹的不确定性问题[4-9],而对靶点相对于井口的定位问题研究甚少。Williamson等[10]提出了采用变比例因子来计算地图投影坐标的方法,以减小因地图投影变形而产生的误差,但是没有研究其他缺陷的改进方法。本文基于地球椭球及其解算原理,提出既规避地图投影变形问题,又使垂向定位与水平面定位相协调的真三维井眼定位方法,从根本上消除现行定位方法的缺陷,精准定位靶点与井口间的相对位置。
1 现行定位方法
1.1 指北基准
井口坐标系是设计和监测井眼轨迹的基础,其首要任务是确定指北基准。定向钻井涉及3个指北方向,即真北、地图投影坐标北和磁北。真北指向地理北极方向,地图投影坐标北指向高斯投影、UTM(通用横轴墨卡托)投影等地图投影平面上的纵坐标轴正向(也简称网格北),而磁北指向地磁北极方向。在井口坐标系中,垂深坐标轴沿重力线方向指向地心,所以选定指北基准后就确定了北坐标轴和东坐标轴的方向。此外,指北基准还是方位角的起算基准,对应于 3个指北基准的方位角分别称之为真方位角、坐标方位角(也称网格方位角)和磁方位角[11-13]。三者之间的关系如图1所示。
由于磁北极随时间变化,所以磁北不宜作为指北基准,否则会给井眼防碰、老井侧钻及油田开发等工作带来不便[11-13]。理论上,真北和坐标北(网格北)都可作为指北基准。由于根据地图投影坐标容易确定井口坐标系下的靶点北坐标和东坐标,据此可直接设计井眼轨道,所以目前习惯采用网格北作为指北基准。
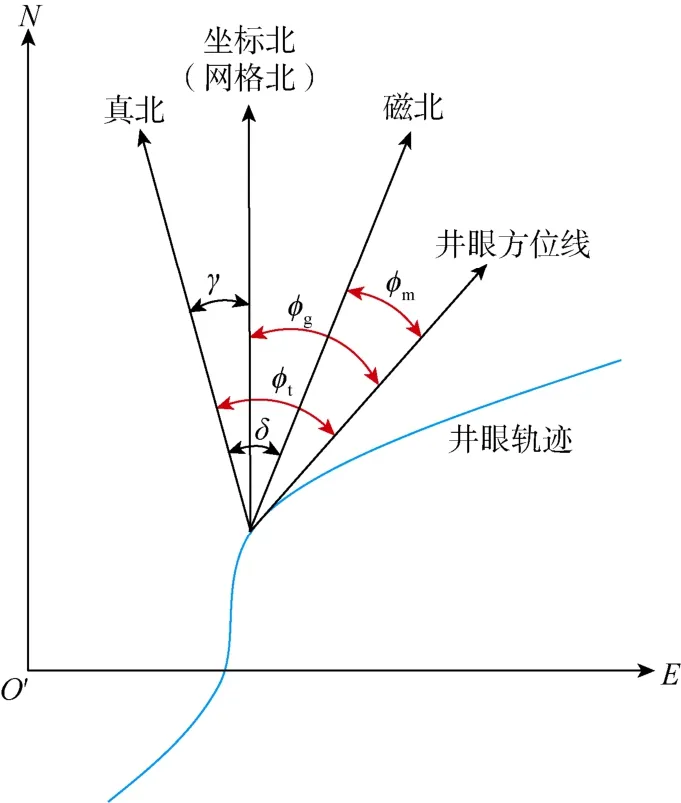
图1 指北基准及方位角
1.2 靶点定位方法
在设计井眼轨迹时,应先确定靶点与井口之间的相对位置。现行定位方法分别采用水平面定位和垂直方向定位来确定靶点在井口坐标系下的空间坐标[1-3]。垂直方向定位用于确定靶点垂深,靶点垂深为井口与靶点的高程之差。水平面定位用于确定靶点的北坐标、东坐标等参数,其定位方法及步骤为:①将井口点和靶点分别沿地球椭球面法线投影到椭球面上,得到大地坐标(L, B);②按地图投影原理及方法,将井口点和靶点分别投影到地图投影平面上,得到投影面上的坐标(x, y)[14-16];③靶点相对于井口的北坐标和东坐标分别为靶点与井口点在地图投影平面上的纵坐标 x之差和横坐标 y之差;④根据靶点北坐标和东坐标,计算靶点的水平位移、平移方位等参数。
确定了靶点在井口坐标系下的空间坐标,便可进行井眼轨迹设计。需要注意的是,此时指北基准为网格北。
2 现行定位方法存在的问题
2.1 水平面及垂向定位
在井口坐标系中,由北坐标轴和东坐标轴所构成的平面被认为是水平面。然而,大地水准面是假想海洋处于完全静止和平衡状态时的海水面,并延伸到大陆内部、包围整个地球的闭合曲面。模型化的地球椭球要求椭球大小和形状应与所研究区域的大地水准面有最佳吻合[14]。也就是说,大地水准面接近于椭球面,并非平面。在很小的区域内,大地水准面可近似为水平面,但并不存在严格意义上的水平面。
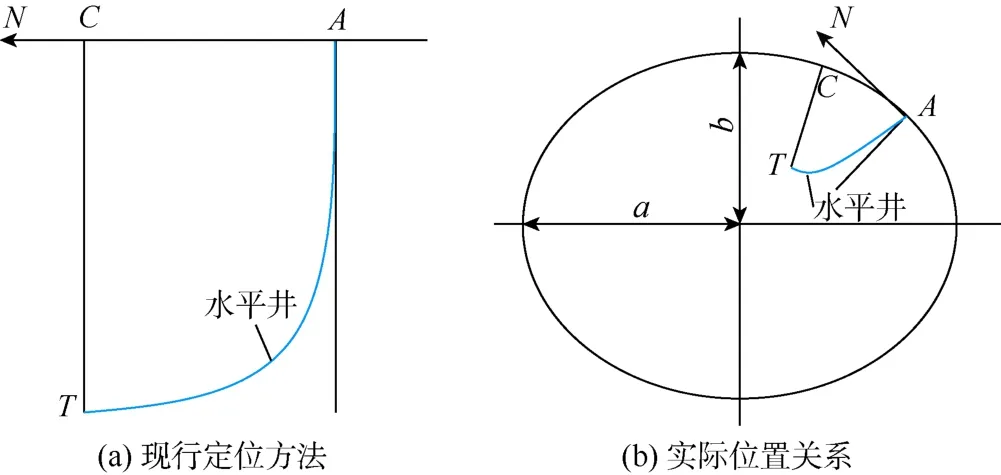
图2 现行定位方法与实际位置关系的对比
如图2所示,假设A和C两点的大地高均为零(在椭球面上),且位于同一个子午面上。如果在A点和C点分别打两口直井,按现行定位方法这两口井将平行向下钻进,但实际情况应是这两口井越来越靠近并相交于地心。特别地,如果A和C两点分别位于赤道和北极上,则这两口井应相互垂直而非平行。显然,对于丛式井而言,现行定位方法不能准确地定位各井间的相互位置关系。
对于同一口井而言,现行定位方法同样存在误差。例如,假设靶点T位于C点的垂直线上,从A点到T点打一口水平井。按现行定位方法计算出的水平位移明显偏大(见图2)。由于现行定位方法采用C点与T点间的高程差来确定T点的垂深,而实际上C点却不在由北坐标轴和东坐标轴所确定的平面上,即C点不在图2b中的北坐标轴N上,而是在子午椭圆上。因此现行定位方法计算出的垂深偏小。显然,按现行定位方法以井口A和靶点T为基础来设计井眼轨迹,其设计结果必然存在误差。
现行定位方法主要存在两个问题:①将大地水准面近似为水平面;②采用水平面定位和垂向定位进行空间定位,但二者相互独立。
2.2 地图投影
首先,投影变形是地图投影的固有缺陷,任何地图投影方法都不可避免地存在长度、方向、角度或面积变形甚至多种变形共存[14]。因此,基于地图投影坐标进行井眼定位必然存在误差,从而影响井眼轨迹设计的精度。此外,由于投影带内不同位置的投影变形程度不同,因此不同位置定向井的设计精度是不同的。
其次,不同国家及地区所采用的地图投影方法不同,且都有各自的大地坐标系。要开发相关的石油工程应用软件,必须涵盖几乎所有的地图投影解算方法及大地坐标系。此外,国际化的石油公司因涉及国外业务,也需要了解不同国家和地区地图投影方法及大地坐标系。因此,现行定位方法增加了不少繁琐的工作。
2.3 方向变形
现行定位方法以网格北为指北基准建立井口坐标系,并进行井眼轨迹设计。在将实钻轨迹归算到井口坐标系时,必然用到子午线收敛角和磁偏角[11-14]。但是,子午线收敛角和磁偏角都与地理位置有关,它们都沿井眼轨迹变化,而现行定位方法只使用一点(通常为井口点)处的子午线收敛角和磁偏角来归算全井的井眼轨迹,显然存在误差。
2.4 大地坐标系
一个国家或地区可能存在多个大地坐标系,例如中国先后建立了 4个国家大地坐标系。一口定向井从设计到施工往往涉及多个部门甚至多家公司,在实际工作中存在忽视甚至误用数据问题。通常,地质勘探与开发部门提供井口和靶点的地图投影坐标,油公司负责钻井工程设计,定向井服务公司提供井眼轨迹监测与控制技术服务。由于相应的数据审查及监管机制尚不完善,各工作环节所使用的大地坐标系及参考基准有可能不一致。例如,当前设计或正在钻进的新井采用2000国家大地坐标系,而几十年前已完钻的邻井采用1954年北京坐标系。因为这两个大地坐标系的参考椭球参数不同,所以应进行包括大地坐标系转换在内的数据归算。然而,在实际工作中时常会忽视这种坐标系转换问题而直接进行井眼防碰等计算,致使计算结果不准确。
3 真三维定位方法
要从根本上解决现行定位方法存在的问题,就必须规避地图投影及其投影变换问题。本文提出的真三维井眼定位方法的总体思路是:采用真北方向作为指北基准,借助地固坐标系建立井口坐标系与大地坐标系及高程坐标之间的转换关系,从而得到靶点相对于井口的空间坐标。
地固坐标系分为参心坐标系和地心坐标系,它们都有大地坐标系和空间直角坐标系两种形式。参心坐标系以参考椭球面为参考面,原点位于参考椭球中心;地心坐标系以总地球椭球面为参考面,原点位于地球质心[14]。如图3所示,地固空间直角坐标系O-XYZ的Z轴为地球椭球的旋转轴,指向地球北极;X轴为起始子午面与赤道面的交线,指向椭球面;Y轴在赤道面内并与X轴正交,指向地理东。
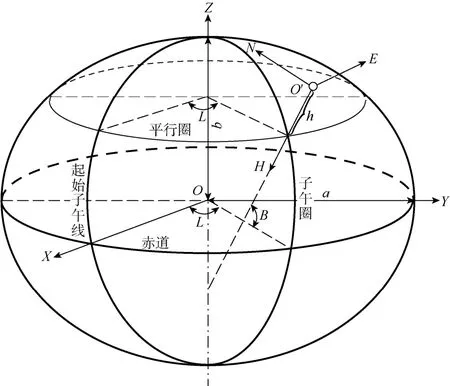
图3 坐标系统及其相互关系
地固空间直角坐标系与大地坐标系及高程坐标之间的转换关系为:
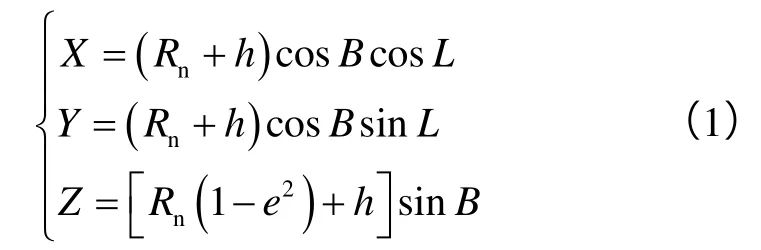
以井口点O′为原点,建立井口坐标系O′-NEH(见图3)。其中,H轴沿垂直方向指向参考椭球中心或地球质心,N轴沿子午线方向指向地理北,E轴垂直于N轴和H轴指向地理东。若井口点的大地坐标为(L0, B0)、地固空间直角坐标为(X0, Y0, Z0),则井口坐标系与地固空间直角坐标系之间的转换关系为:
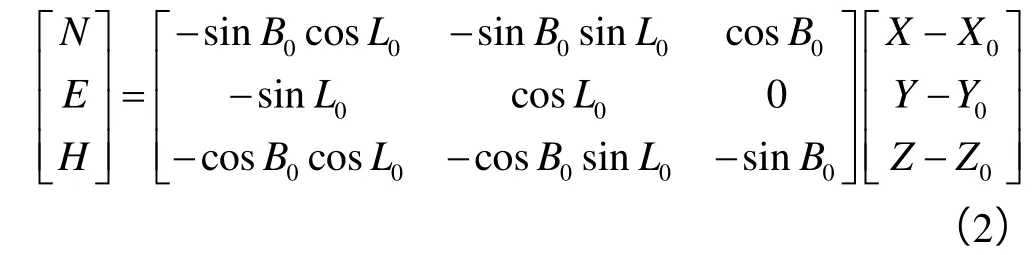
这样,根据井口点O′和靶点T的大地坐标及大地高(L0, B0, h0)和(LT, BT, hT),先由(1)式分别计算出地固空间直角坐标(X0, Y0, Z0)和(XT, YT, ZT),再由(2)式计算出靶点在井口坐标系下的坐标(NT, ET, HT),便可确定靶点相对于井口的空间位置。
真三维井眼定位方法基于地球椭球及其坐标变换进行靶点定位,不涉及地图投影及投影变换问题。不仅消除了因地图投影变形而产生的误差,而且规避了因忽视或遗漏不同大地坐标系间换算而带来的误差风险,能显著提高井眼轨迹设计与监测的精度和可靠性。
4 算例分析
地球椭球的几何参数是井眼定位的基础数据。不同国家及地区所采用的参考椭球不同,对定位精度的影响程度也不同,在此不予赘述。这里主要讨论不同地理位置以及靶点与井口相对位置条件下,现行定位方法的误差情况,也可理解为真三维井眼定位方法的定位精度提高程度。采用中国2000国家大地坐标系,其参考椭球的长半轴 a=6 378 137.0 m,短半轴 b= 6 356 752.314 1 m,扁率为1/298.257 222 101。
4.1 不同地理位置
假设在不同地理位置有 3口水平井,其井口和靶点的大地坐标及大地高数据见表1。按现行定位方法,先根据高斯投影公式算得井口和靶点的投影纵横坐标及子午线收敛角,再算得井口坐标系下的靶点坐标,结果见表2。按真三维井眼定位方法,先算得地固空间直角坐标系下的井口和靶点坐标,再算得井口坐标系下的靶点坐标,结果见表3。
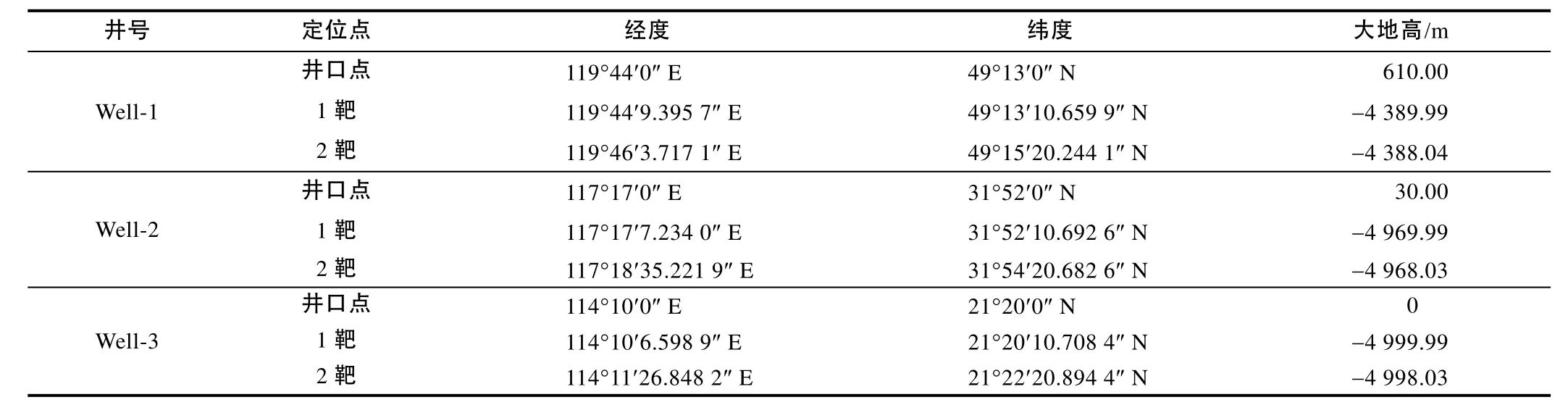
表1 大地坐标及大地高数据

表2 现行定位方法的计算结果
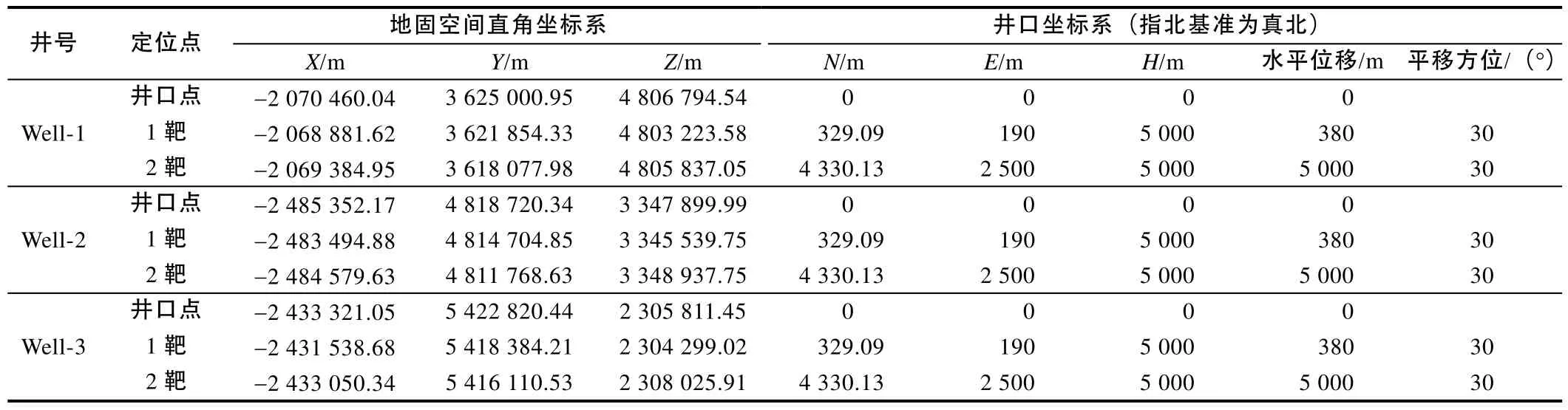
表3 真三维定位方法的计算结果
按真三维定位方法,该算例中 3口水平井具有相同的靶点垂深、水平位移及平移方位(见表3)。但是,因为它们的地理位置不同(位于20号地图投影带的不同位置),地图投影变形的程度不同,所以按现行定位方法算得的靶点垂深、水平位移及平移方位不同(见表2),子午线收敛角数值也不同。
4.2 不同靶点相对位置
假设某定向井的井口经度为 84°30′0″ E、纬度为41°0′0″ N、大地高为1 000 m。当靶点与井口之间的相对位置发生变化时,即在不同靶点垂深、水平位移、平移方位条件下,现行定位方法与真三维定位方法的计算结果见表4—表6。
由表4—表6可知:①靶点经度、纬度、大地高与靶点垂深、水平位移、平移方位这两组数据之间存在复杂的相互影响规律;②现行定位方法算得的靶点垂深偏小、水平位移偏大;③由于地球椭球的扁率很小,所以无论是现行定位方法还是真三维定位方法,靶点垂深和水平位移随平移方位的变化都很小。

表4 不同靶点垂深条件下的计算结果

表5 不同靶点水平位移条件下的计算结果
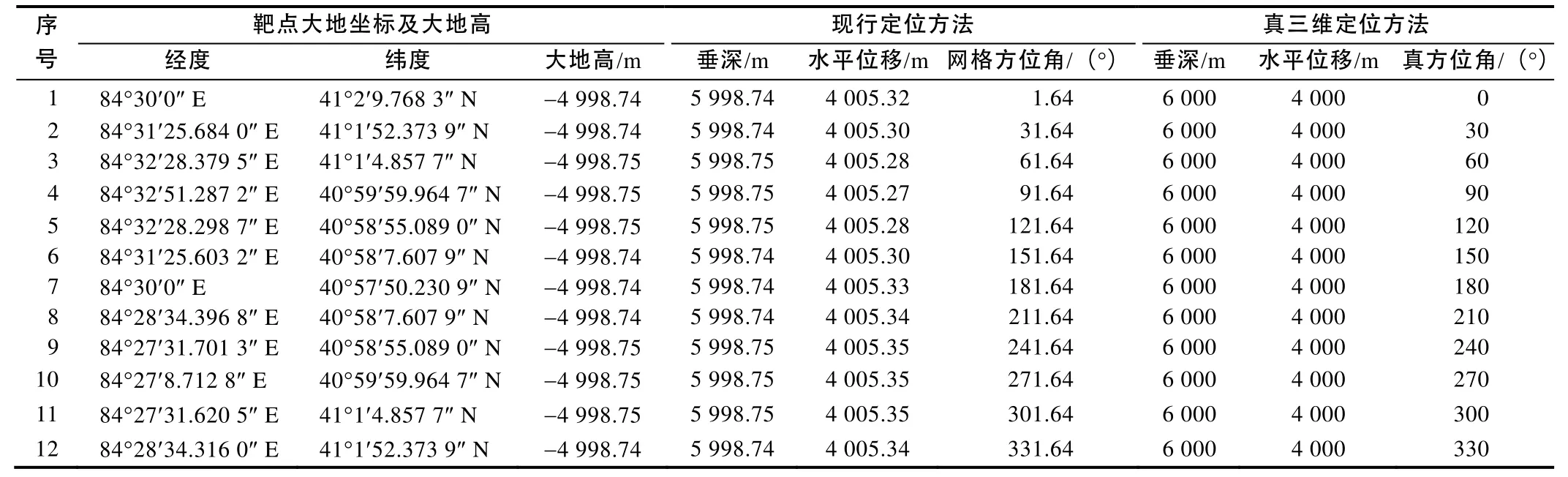
表6 不同靶点平移方位条件下的计算结果
5 结论
现行井眼定位方法采用网格北作为指北基准,但由于子午线收敛角和磁偏角都沿井眼轨迹变化,且井口坐标系只能使用一点处的子午线收敛角和磁偏角来归算全井的井眼轨迹,必然存在误差,因此采用真北作为指北基准更为科学。
现行定位方法基于地图投影坐标进行水平面定位,而投影变形是地图投影的固有缺陷,所以存在无法规避的定位误差。现行定位方法基于高程进行垂向定位,其靶点垂深只与靶点及井口的大地高有关,而与大地坐标无关,不符合实际。现行定位方法采用水平面定位和垂向定位相结合的方法来确定靶点与井口之间的相对位置,但两者却相互独立。算例分析也表明现行定位方法存在较大误差,计算的靶点垂深偏小,水平位移偏大。
真三维井眼定位方法基于地球椭球进行靶点与井口间相对位置的空间定位,不涉及地图投影问题,从根本上解决了现行定位方法存在的问题,能显著提高井眼轨迹设计与监测的精度和可靠性。
符号注释:
a——地球椭球的长半轴,m;b——地球椭球的短半轴,m;B——大地纬度,(°);e——地球椭球的第一偏心率,无因次;h——大地高,m;L——大地经度,(°);N,E,H——井口坐标系的北坐标、东坐标和垂向坐标,m;Rn——卯酉圈的曲率半径,m;x——地图投影平面上的纵坐标,m;y——地图投影平面上的横坐标,m;X,Y,Z——地固空间直角坐标系的坐标,m;γ——子午线收敛角,(°);δ——磁偏角,(°);φg——网格方位角,(°);φm——磁方位角,(°);φt——真方位角,(°)。下标:0——井口点;T——靶点。
[1] 韩志勇. 定向钻井设计与计算[M]. 2版. 东营: 中国石油大学出版社, 2007. HAN Zhiyong. Design and calculation of directional drilling[M]. 2nd ed. Dongying: China University of Petroleum Press, 2007.
[2] 刘修善. 井眼轨道几何学[M]. 北京: 石油工业出版社, 2006. LIU Xiushan. Geometry of wellbore trajectory[M]. Beijing: Petroleum Industry Press, 2006.
[3] 国家能源局. 定向井轨道设计与轨迹计算: SY/T 5435—2012[S].北京: 石油工业出版社, 2012. National Energy Administration. Wellpath planning & trajectory calculation for directional wells: SY/T 5435—2012[S]. Beijing: Petroleum Industry Press, 2012.
[4] JAMIESON A. Introduction to wellbore positioning[M/OL]. Inverness, Scotland: University of the Highlands & Islands, 2012[2016-04-25]. https://www.uhi.ac.uk/en/research-enterprise/wellbore-positioningdownload.
[5] WILLIAMSON H S. Accuracy prediction for directional measurement while drilling[J]. SPE Drilling & Completion, 2000, 15(4): 221-233.
[6] MACMILLAN S, GRINDROD S. Confidence limits associated with values of the earth’s magnetic field used for directional drilling[J]. SPE Drilling & Completion, 2010, 25(2): 230-238.
[7] MAUS S, NAIR M C, POEDJONO B, et al. High definition geomagnetic models: A new perspective for improved wellbore positioning[R]. SPE 151436, 2012.
[8] 史鸿祥, 李辉, 郑多明, 等. 基于随钻地震测井的地震导向钻井技术: 以塔里木油田哈拉哈塘区块缝洞型储集体为例[J]. 石油勘探与开发, 2016, 43(4): 662-668. SHI Hongxiang, LI Hui, ZHENG Duoming, et al. Seismic guided drilling technique based on seismic while drilling (SWD): A case study of fracture-cave reservoirs of Halahatang block, Tarim Oilfield, NW China[J]. Petroleum Exploration and Development, 2016, 43(4): 662-668.
[9] BROOKS A G, WILSON H. An improved method for computing wellbore position uncertainty and its application to collision and target intersection probability analysis[R]. SPE 36863, 1996.
[10] WILLIAMSON H S, WILSON H F. Directional drilling and earth curvature[J]. SPE Drilling & Completion, 2000, 15(1): 37-43.
[11] 刘修善, 王继平. 基于大地测量理论的井眼轨迹监测方法[J]. 石油钻探技术, 2007, 35(4): 1-5. LIU Xiushan, WANG Jiping. A method for monitoring wellbore trajectory based on the theory of geodesy[J]. Petroleum Drilling Techniques, 2007, 35(4): 1-5.
[12] 刘修善. 定向钻井中方位角及其坐标的归化问题[J]. 石油钻采工艺, 2007, 29(4): 1-5. LIU Xiushan. Naturalization of azimuth angles and coordinates in directional drilling[J]. Oil Drilling & Production Technology, 2007, 29(4): 1-5.
[13] 刘修善. 定向钻井轨道设计与轨迹计算的关键问题解析[J]. 石油钻探技术, 2011, 39(5): 1-7. LIU Xiushan. Analysis of the key issues involved in wellpath planning and trajectory calculation for directional drilling[J]. Petroleum Drilling Techniques, 2011, 39(5): 1-7.
[14] 孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010. KONG Xiangyuan, GUO Jiming, LIU Zongquan. The fundamentals of geodesy[M]. 2nd ed. Wuhan: Wuhan University Press, 2010.
[15] 孙达, 蒲英霞. 地图投影[M]. 南京: 南京大学出版社, 2012. SUN Da, PU Yingxia. Map projection[M]. Nanjing: Nanjing University Press, 2012.
[16] 王美玲, 付梦印. 地图投影与坐标变换[M]. 北京: 电子工业出版社, 2014. WANG Meiling, FU Mengyin. Map projection and coordinate transformation[M]. Beijing: Publishing House of Electronics Industry, 2014.
(编辑 胡苇玮)
A true three-dimensional wellbore positioning method based on the earth ellipsoid
LIU Xiushan
(Sinopec Research Institute of Petroleum Engineering, Beijing 100101, China)
In view of the problems existing in the current wellbore positioning method, a true three-dimensional wellbore positioning method was presented, and an example for analysis was given. The current positioning method uses the grid north as the reference datum to the north, positions in the horizontal plane based on the map projection coordinates, and positions in the vertical direction based on the elevation coordinates. It has inherent defects and errors, as the two positionings above are independent of each other, and only use the constant meridian convergence and constant magnetic declination at the wellhead to calculate the borehole trajectory for the whole well. Based on the earth ellipsoid and its calculating principle, the transformation relationship between the wellhead coordinate system, geodetic coordinate system and elevation coordinate system was revealed, and the true three-dimensional wellbore positioning method using the true north as the reference datum to the north was presented. Analysis results of an example show that the current positioning method yields a smaller vertical depth and a larger horizontal displacement for the target, and produces larger errors compared with the true three-dimensional positioning method. The true three-dimensional positioning method has fundamentally solved the problems existing in the current positioning method, accurately positioning the relative location between the target and the wellhead, and significantly improves the accuracy and reliability of borehole trajectory design.
drilling theory; directional drilling; wellbore trajectory; wellbore positioning
国家科技重大专项“海相碳酸盐岩油气井井筒关键技术”(2011ZX05005-006)
TE21
A
1000-0747(2017)02-0275-06
10.11698/PED.2017.02.13
刘修善(1962-),男,黑龙江牡丹江人,博士,中国石化石油工程技术研究院教授级高级工程师,主要从事导向钻井工艺、井下信息测量与控制等方面的研究工作。地址:北京市朝阳区北辰东路 8号北辰时代大厦9层,中国石化石油工程技术研究院,邮政编码:100101。E-mail:liuxs.sripe@sinopec.com
2016-06-22
2016-10-12
