MHD Stagnation Point Flow of Williamson Fluid over a Stretching Cylinder with Variable Thermal Conductivity and Homogeneous/Heterogeneous Reaction

M.Bilal,M.Sagheer,S.Hussain,and Y.Mehmood

Department of Mathematics,Capital University of Science and Technology,Islamabad,Pakistan

Nomenclature

?

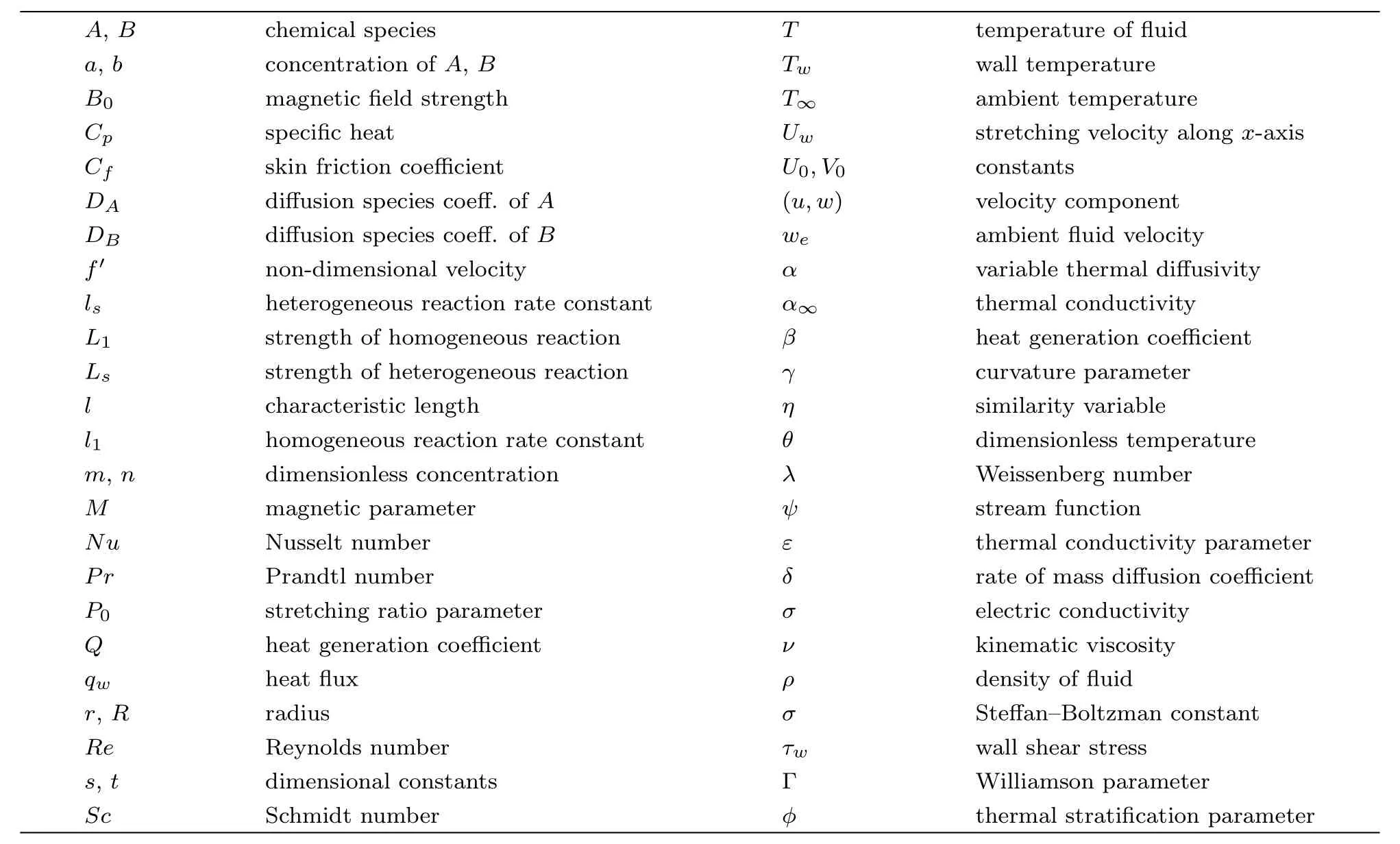
1 Introduction

Heat transfer analysis over a stretching cylinder is one of the current research topic among researchers due to its extensive applications in many engineering processes.In available literature,usually the thermal conductivity is taken as constant.Heat is transferred due to difference in temperature.If there is a large temperature difference then assumption of constant thermal conductivity will lead to a noticeable error.Thus to minimize this type of error,it is necessary to consider a temperature dependent variable thermal conductivity within the thermal boundary layer region.Hussain et al.[1]analyzed the effect of MHD Jeffrey fluid flow on heat transfer with variable thermal conductivity.They used the inclined magnetic field on peristaltic flow and obtained solution analytically using perturbation method.Lin et al.[2]presented the numerical solution of unsteady pseudo-plastic nanoliquid in a thin if lm flow over a linearly stretching surface.They considered the effect of viscous dissipation and variable thermal conductivity along with four different types of nanoparticles.Influence of variable thermal condutivity on an exponentially stretching sheet for third grade fluid using inclined magnetic field was addressed by Hayat et al.[3]In another article,Hayat et al.[4]documented the behaviour of mixed convection and variable thermal conductivity on viscoelastic nano fluid over a stretching cylinder with heat source/sink.Si et al.[5]explored numerically the laminar film condensation of non-Newtonian pseudo-plastic fluid on an isothermal vertical plate with variable thermal conductivity.Malik et al.[6]made an attempt,which deals with the heat transfer analysis of Williamson fluid over a stretching cylinder with heat generation/absorption and variable thermal conductivity.They conclude that increase in the thermal conductivity parameter enhances the temperature.References[7–10]include some recent work related to variable thermal conductivity.

An extensive literature can be found regarding non-Newtonian fluid flows over a stretching cylinder because of their industrial and engineering applications such as metallurgical processes,extraction of petroleum,pipe industry,and many others. Several models have been proposed to analyze the pseudo-plastic fluids(e.g.Cross model,Carreau model,Power law model,Ellis model and Williamson fluid model).Every model has its own characteristics.In Williamson fluid model,a variable viscosity of larger range can be considered.Williamson[11]introduced a model that describes the pseudo-plastic materials and fluid flow experimentally.Malik and Salahuddin[12]used the Williamson fluid model over a stretching cylinder with the effect of magnetohydrodynamics. Solutions are obtained by shooting method for the fluid flow.Malik et al.[13]discussed the flow and heat transfer of Williamson fluid over a stretching cylinder with homogeneous/heterogeneous reaction using Keller–Box method.In another article,Salahuddin et al.[14]have numerically investigated the MHD flow of Williamson fluid with Cattaneo–Christov heat flux model over a non-linear stretching surface.Explicit finite difference method is employed for the numerical solutions.Hayat et al.[15]offered an overview of the literature about MHD boundary layer flow of Williamson fluid with Ohmic dissipation and thermal radiation.They noticed the decreasing influence of Weissenberg number on velocity pro file.A list of references concerning Williamson fluid can be found in Refs.[16–18].

A phase is a distinct,uniform state of a system that has no observable boundary,which may divide the system into components. Chemical reactions are broadly classified into homogenous reactions(occurring in single phase)and heterogeneous reactions(involving multiple phases).A reaction is often aided with a catalyst,which enhances the reaction rate by providing a substitute path for reaction having lower activation energy.In recent years,scientists are very much concerned in creating effective and efficient processes that include an amalgamation of both homogenous and heterogeneous reactions.The researchers are currently much concerned with the study of the complex interactions of these reactions.Hayat et al.[19]explored Jeffrey fluid flow with homogeneous/heterogeneous reaction using Cattaneo–Christov heat flux model.They conclude that concentration of molecules increases with the increment of Schmidt number.On another article Hayat et al.[20]presented an analytical solution of Oldroyd-B fluid with MHD and homogeneous/heterogenenous reaction using Cattaneo–Christov heat flux model.Reddy et al.[21]analyzed the effect of homogeneous/heterogenenous reaction on MHD and non-linear thermal radiation between rotating plates.They employed shooting technique to solve the problem.Homogeneous/heterogenenous reaction in magneto-nano fluid in a permeable shrinking surface was addressed by Mansur et al.[22]Kameswaran et al.[23]explored homogeneous/heterogenenous reaction in a viscous nano fluid flow past a stretching sheet analytically when the auto catalyst and diffusion coefficients of the reactants are equal.

In all the above mentioned articles,thermal conductivity is considered as a constant. Very less work is available with variable thermal conductivity specially in stretching cylinder.Our interest in the present article is to analyze the work of Malik et al.[13]with the assumption of variable thermal conductivity,magnetohydrodynamics and heat generation/absorption.Williamson fluid is considered over a stretching cylinder with homogeneous/heterogeneous reaction. Solutions for flow and heat transfer are computed numerically by shooting method[24−28]integrated with Runge–Kutta method of order four.Numerical solutions are further supported with MATLAB built-in function bvp4c.Graphical results of velocity,temperature and concentration are presented and also numerical results of skin-friction coefficient and local Nusselt number are tabulated for emerging parameters.

2 Mathematical Formulation

We have considered MHD stagnation point flow of Williamson fluid under the combined effect of homogeneous/heterogeneousreaction and heatgeneration/absorption over a linearly stretching cylinder alongz-axis.Mangetic field of strengthB0is applied normal to the flow as shown in Fig.1.Induced magnetic field is neglected because of the supposition of small Reynolds number.Further a variable thermal conductivity and the effect of thermal strati fication at boundary layer flow are also incorporated.

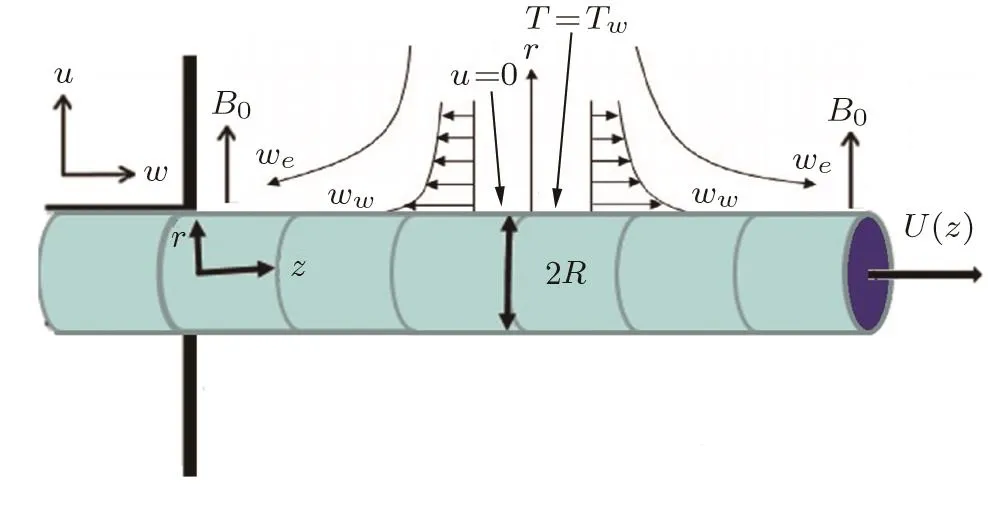
Fig.1 Geometry of the Problem.

It is also clear that temperature at the sheetTwis greater than the temperature far away from the sheetT∞.There is an isothermal cubic auto catalytic(homogeneous)reaction on boundary layer flow however first order reaction(heterogeneous)is taken on catalyst surface.These are represented by

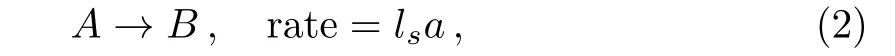
wherel1,lsare rate constants anda,bdenote concentrations of the chemical speciesA,Brespectively.Further considering that there is no change in temperature for both the reactions.Employing boundary layer approximations and taking in account all considerations mentioned above,the governing equations of the system,are

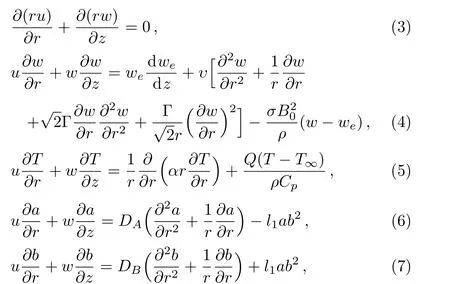
subject to the boundary conditions

Using the following transformations

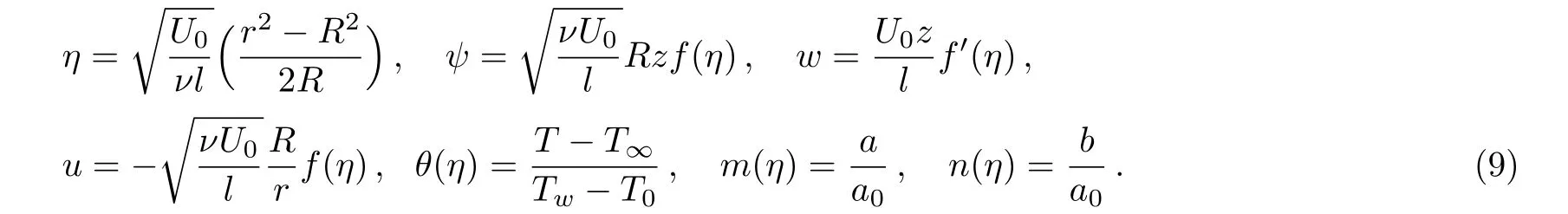
In Eq.(5),αis variable thermal conductivity,which is defined as

satisfaction of Eq.(3)is evident,however Eqs.(4),(5),(6),and(7)lead to the following non-dimensional form

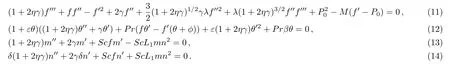
The transformed boundary conditions are:

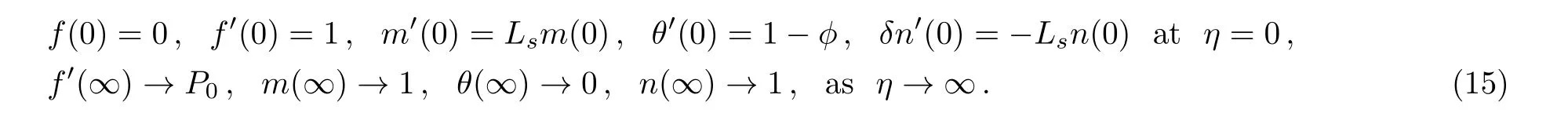
Different dimensionless parameters appearing in Eqs.(11)–(15),are defined as

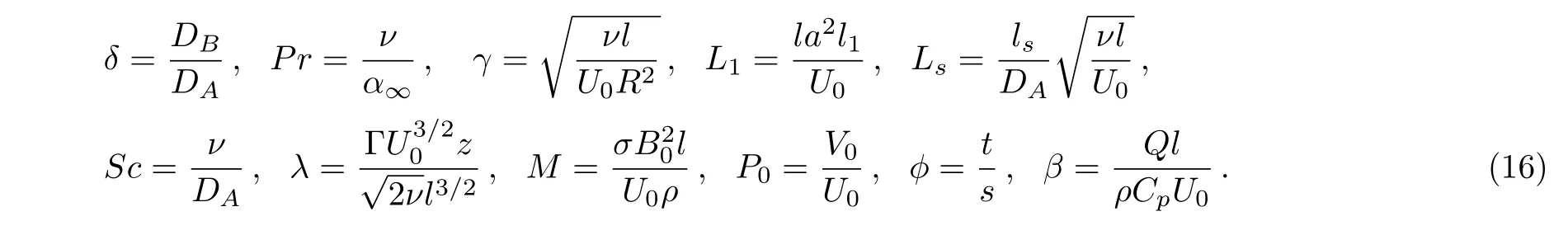
Assumption that diffusion coefficient of chemical speciesAandBare of analogous magnitude leads us to suppose thatDAandDBare identical providedδ=1.Thus,we have

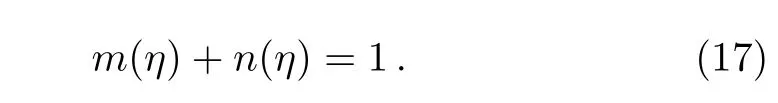
Using Eq.(17),Eqs.(13)and(14)take the form

and the corresponding boundary conditions for Eq.(18)are

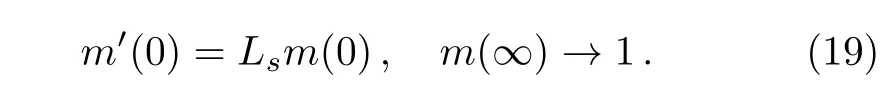
Skin friction coefficient and Local Nusselt number in dimensional form are

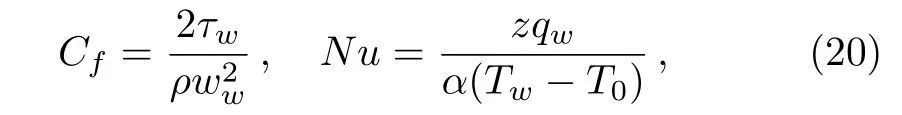
whereτwandqware the shear stress and surface heat flux given by

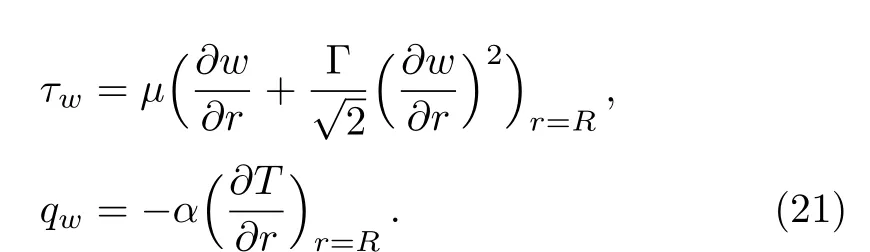
The dimensionless form of skin friction coefficient and local Nusselt number are represented as

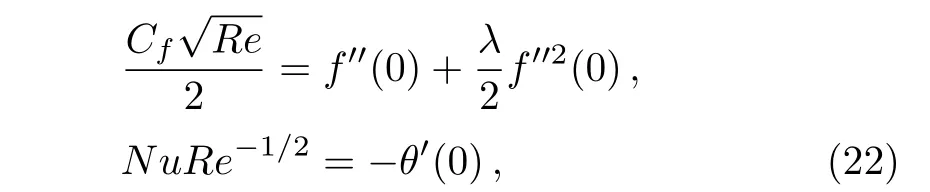
whereRe=U0z2/νl.

3 Solution Methodology

Non-linear system of ordinary differential equations obtained from partial differential equations,is solved numerically by shooting method with integration scheme of Runga–Kutta method of order four.To solve the system(11),(12)and(18)with respective boundary conditions,first we have to convert it into a system of first order ordinary differential equations.Afterwards,the missing conditionsι1,ι2andι3are supposed initially and then refined iteratively by Newtons iterative scheme subject to the tolerance of 10−6.For numerical computations,the largest value ofηhas been taken asη=8 instead ofη→ ∞because values ofηgreater thanη=8 do not make a considerable difference.The results are further strengthened by using bvp4c,a built-in MATLAB function.For first order initial value problem we have denotedfbyy1,θbyy4andmbyy6to have the following equations.

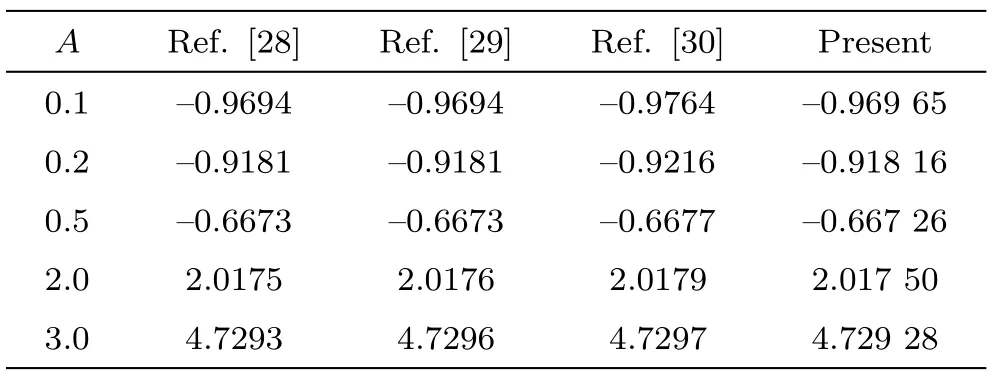
Table 1 Comparison of skin friction coefficient with the previously published work for different values of P0 when γ =0,λ =0,M=0,θ =0,m=0 for f′′(0).

This system of first order initial value problem with the supposition of missing initial conditions is solved with Runge–Kutta method of order four. Newton iterative scheme helps us to refine the initial guesses until the following stoping criteria is met

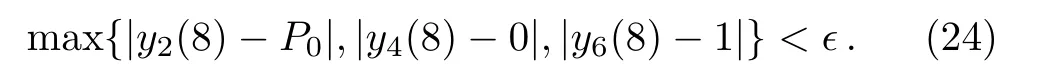
Numerical solutions are obtained and for the purpose of verification of the code,a comparison with some published work is presented in Table 1,where a very good agreement in the results can be seen.

4 Results and Discussions

Numerical solutions for the derived system of equations with associated boundary conditions are obtained by using shooting method.The results are verified by MATLAB built-in function bvp4c.The numerical results of skin friction coefficient and Local Nusselt number for various values of different parameters are enumerated in Table 2.It is evident from the table that friction factor increases with the increasing values of magnetic parame-terMand curvature parameterγ.A reverse behaviour is noticed in case of dimensionless Weissenberg numberλand stretching ratio parameterP0as both have decreasing tendency for the skin friction coefficient.A rise in values of curvature parameterγ,magnetic parameterMand Weissen berg numberλ,depreciates the local Nusselt number while raising the stretching ratio parameterP0enhances the rate of heat transfer in fluid.

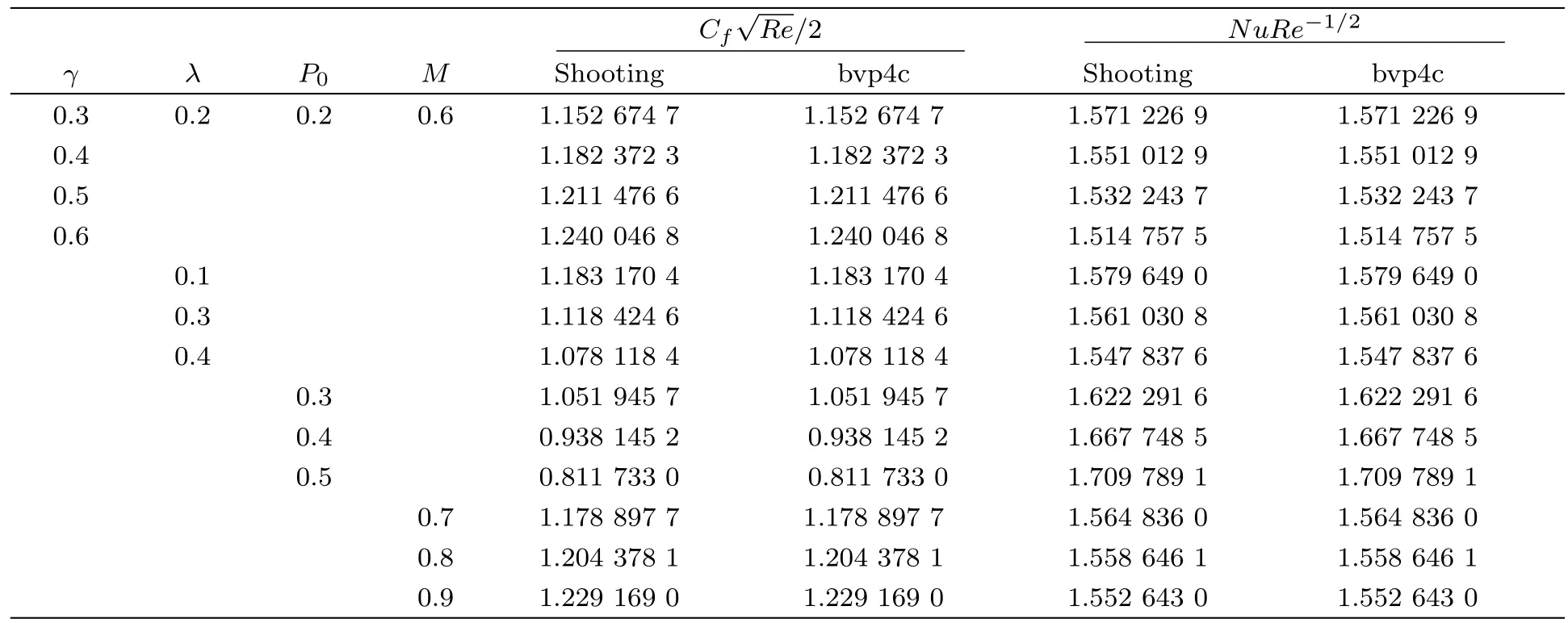
Table 2 Numerical values of Skin friction coefficient and local Nusselt number for different values of parameters when ε =0.2,Pr=0.72,β =0.1,and ϕ =0.3.

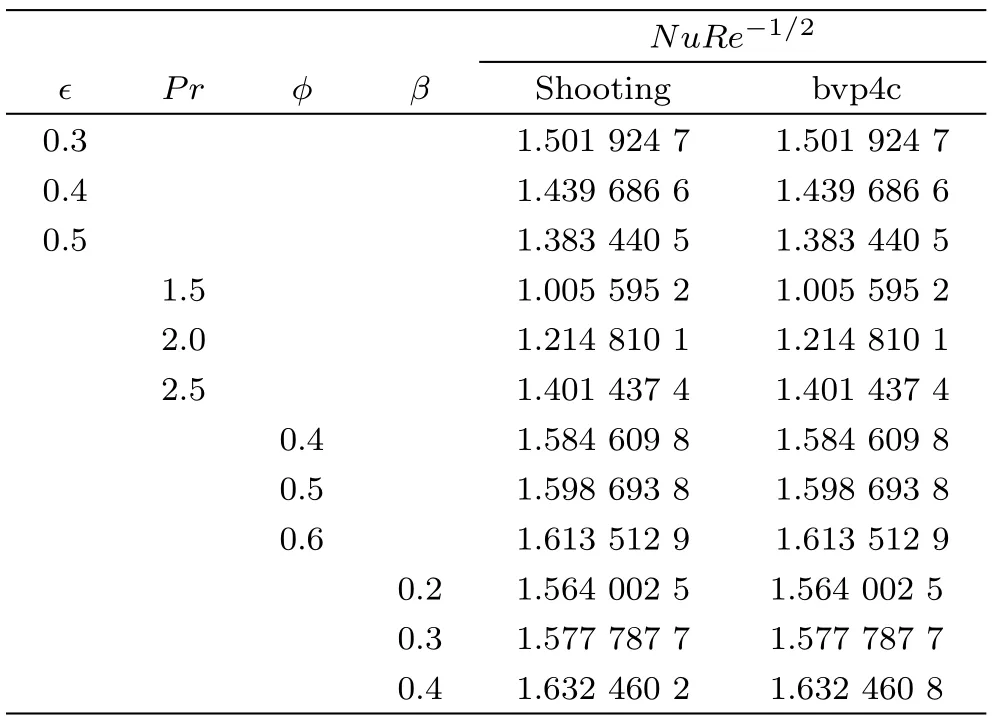
Table 3 Numerical values of local Nusselt number for different values of parameters when γ =0.3,λ =0.2 and P0=0.2,M=0.6.

In Table 3,the effect of thermal conductivity parameterε,Prandtl numberPr,thermal strati fication parameterϕand heat generation/absorption parameterβon heat transfer rate are presented.It is observed from the table that increase in thermal conductivity will reduce the heat transfer rate and hence the temperature increases.On the other hand Nusselt number enhances with the enhancement of Prandtl numberPr,thermal strati fication parameterϕ,and heat generation/absorption parameterβ.

Fig.2 Influence of γ on f ′.

The effects of curvature parameterγ,dimensionless Weissenberg numberWe,magnetic parameterM,and stretching ratio parameterP0on velocity pro file are displayed through Figs.2–5.In Fig.2,values of velocity functionf′(η)and the boundary layer thickness increase by increasingγ.Increase inγimplies reduction in radius of cylinder and hence the speed of the fluid got fasten.Figure 3 elucidates the behaviour of Weissenberg number on velocity pro file.Velocity reduces slightly whenλis raised.As we know that Weissenberg numberλis the ratio of relaxation time to specific process time.Increase in relaxation time will increase the resistance of the fluid and resultantly velocity reduces.In Fig.4,influence of magnetic parameterMon velocity pro file is displayed,which shows the reduction in speed of the fluid with increasingM.It happens due to the retarding force known as Lorenth force,which is a resistive force.Influence of stretching ratio parameterP0on velocity pro file is displayed in Fig.5.As the values ofP0increase,the velocity and the boundary layer thickness increase.

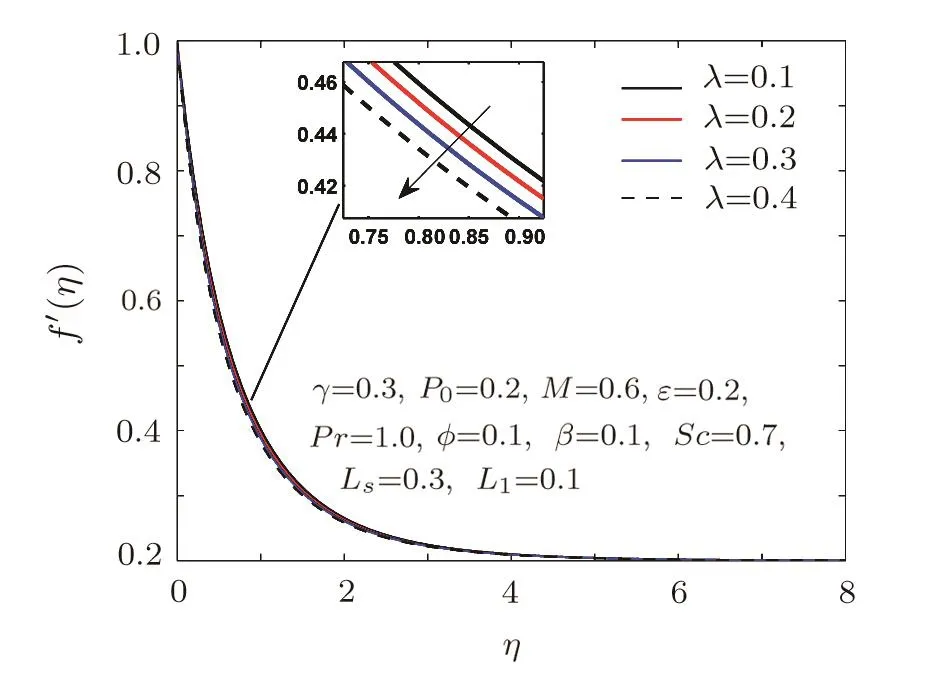
Fig.3 Influence of λ on f ′.

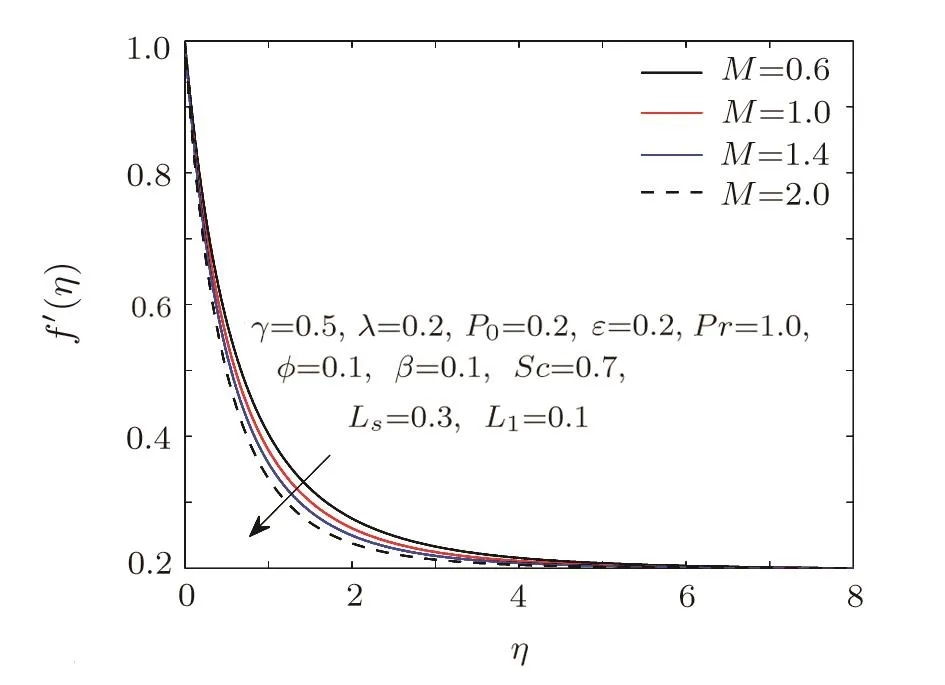
Fig.4 Influence of M on f′.

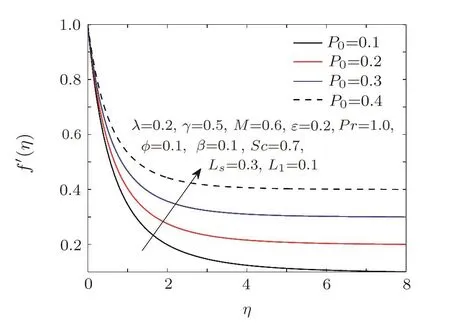
Fig.5 Influence of P0on f′.

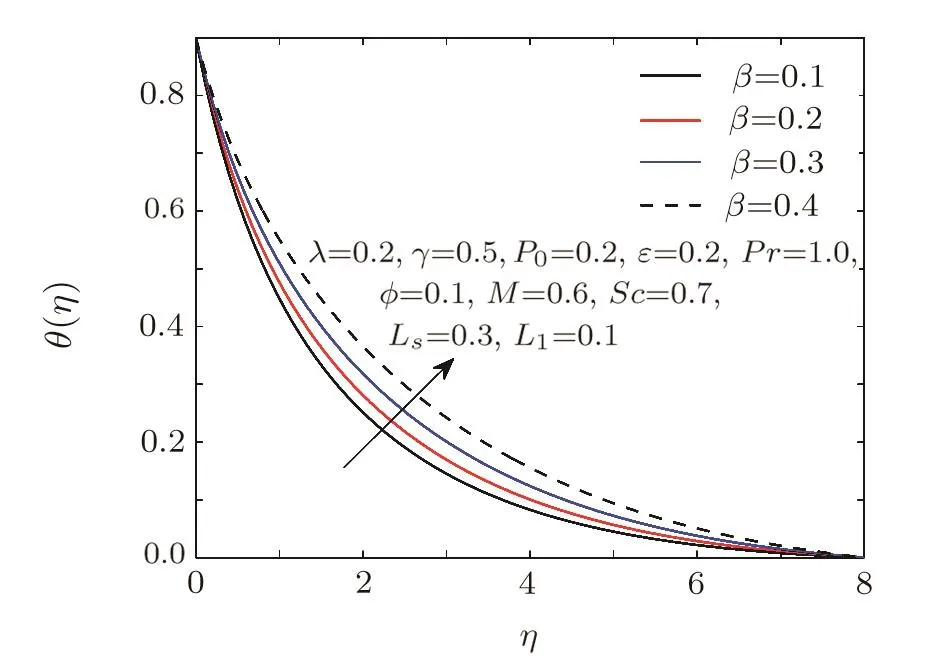
Fig.6 Influence of β on θ.

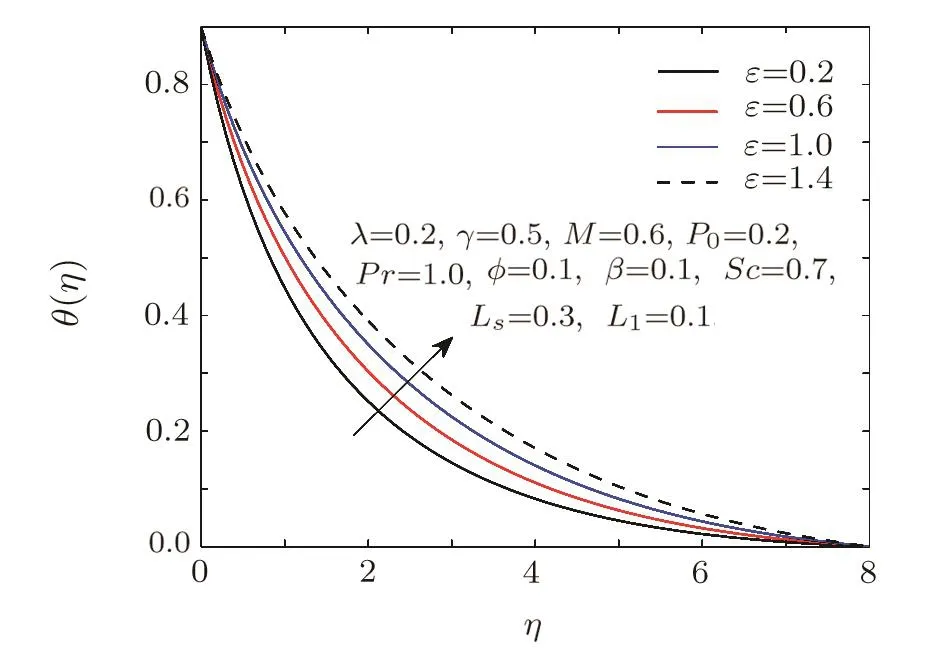
Fig.7 Influence of ϵ on θ.

Fig.8 Influence of γ on θ.

Figures 6–12 show the variations of different parameters on temperature pro file.Figure 6 demonstrates the effect of heat generation/absorption coefficient.As expected temperature increases with the increment of heat generation.Same effect is seen for the thermal conductivity parameterε.As increase in thermal conductivity will definitely raise the temperature of the fluid and this can be con firmed from Fig.7.Influence of curvature parameterγon temperature pro file is depicted in Fig.8.As increase in curvature parameter will reduce the radius of the cylinder,which causes less resistance to the fluid flow but due to the smaller diameter the resistive force between the fluid and wall of the cylinder is enhanced and consequently the temperature increases near the wall.

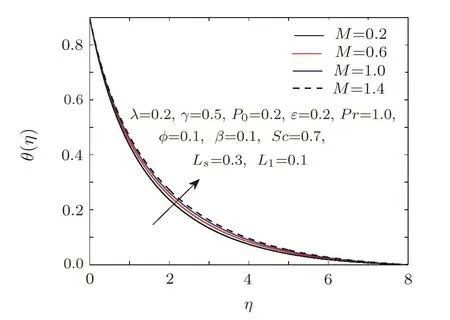
Fig.9 Influence of M on θ.

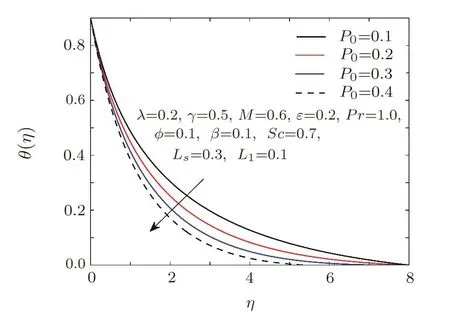
Fig.10 Influence of P0on θ.

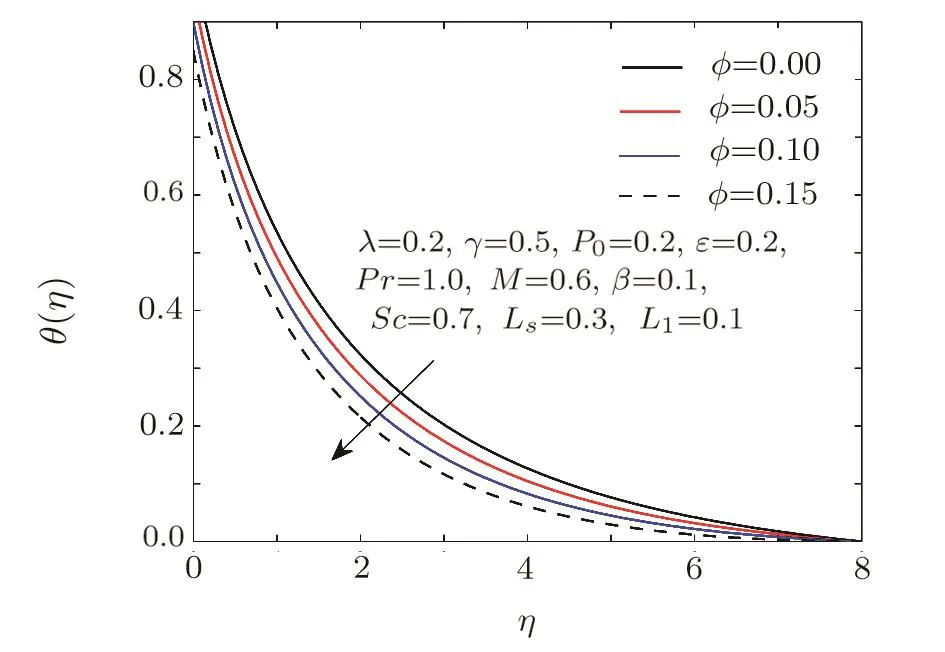
Fig.11 Influence of ϕ on θ.

Figure 9 is plotted to see the impact of magnetic parameterMon dimensionless temperature.Magnetic parameter produces a resistive force in the fluid motion due to Lorentz force.This frictional force enhances the temperature of the fluid.Variation of velocity stretching ratio parameterP0on temperature pro file is illustrated in Fig.10.As we know thatP0is the ratio of far away velocity to the surface velocity and it is also obvious that surface velocity is always greater than ambient velocity,so increase in stretching ratio implies reduction in temperature distribution.

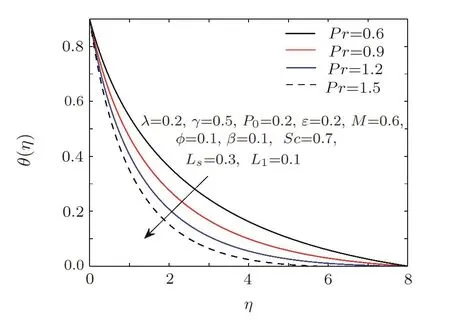
Fig.12 Influence of Pr on θ.

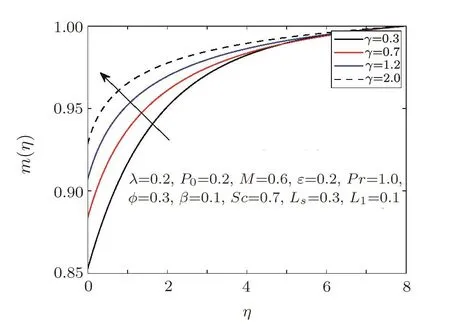
Fig.13 Influence of γ on g(η).

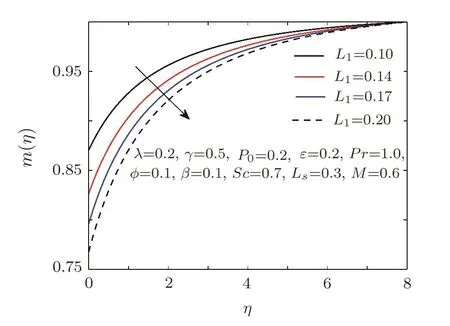
Fig.14 Influence of L1on g(η).

Figure 11 is plotted to portray the behaviour of thermal strati fication parameterϕon temperature pro file.En-hancement in thermal strati fication yields higher the density of the fluid in lower region and it increases on upper region.So the temperature differences deliberately reduces between the cylinder and ambient fluid and this effect clearly elaborated through Fig.11.Figure 12 indicates that the temperature of the fluid decreases for increasing values ofPr.It is contemplated that raising the Prandtl number decreases the thermal diffusivity and hence the thermal boundary layer,which eventually enhances the rate of heat transfer.

Fig.15 Influence of Lson g(η).

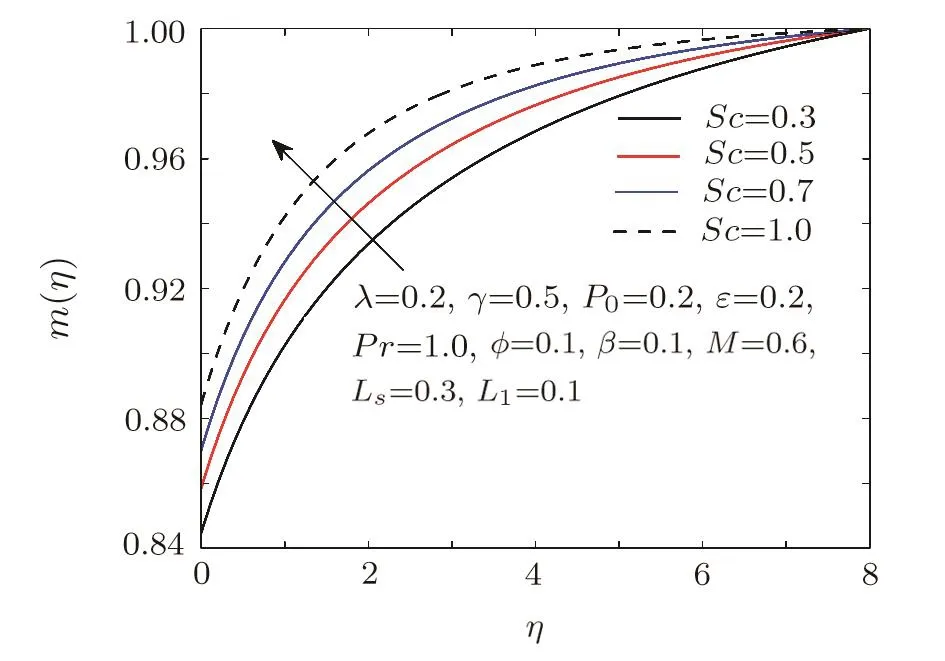
Fig.16 Influence of Sc on g(η).

Figures 13–16 are plotted to analyze the behaviour of concentration pro file subject to variation of different parameters.Figure 13 shows the increasing effect of curvature parameter on concentration.Increasing curvature certainly reduces the radius of cylinder and hence more fluid is expected to flow,which will enhance the mass transfer.Figures 14 and 15 portray the effect of strength of homogeneous/heterogeneous reaction on concentration pro file.It is observed that bothL1andLShave decreasing behaviour but the boundary layer thickness is increased.Influence of Schmidt numberScon mass distribution is shown in Fig.16.Accession of mass concentration is noted for raising Schmidt number.Schmidt number is actually the ratio of momentum diffusivity to mass diffusivity.Increase in Schmidt number will enhance the momentum diffusivity,which resultantly raises the mass distribution.Figure 17 is plotted to see the effect of Weissenberg numberλon temperature distribution.A minor increase in temperature distribution is observed for increasing Weissenberg number.

Fig.17 Influence of λ on θ(η).

5 Concluding Remarks

In the present article,we have numerically investigated the effect of stagnation point flow of Williamson fluid over a stretching cylinder with the effect of homogenous/heterogenous reaction,magnetohydrodynamics and variable thermal conductivity.Shooting technique is summoned to address the system of equations with high nonlinearity.The main findings of the present investigation are summarized as below.

•Homogenous and heterogenous reactions show opposing behaviour on concentration distribution.

•Temperature field is growing function of thermal conductivity and heat generation coefficient.

•Prandtl number and thermal strati fication have the similar impact on local Nusselt number.

•Increasing the values of magnetic parameter boost the temperature and its allied boundary layer thickness.

•Mass distribution is increasing function of Schmidt number.

References

[1]Q.Hussain,S.Asghar,T.Hayat,and A.Alsaedi,Appl.Math.Mech.Engl.Ed.36(2015)499.

[2]Y.Lin,L.Zheng,and G.Chen,Power Technol.274(2015)324.

[3]T.Hayat,Anum Shafiq,A.Alsaedi,and S.Asghar,AIP Adv.5(2015)087108.

[4]T.Hayat,M.Waqas,S.A.Shehzad,and A.Alsaedi,Int.J.Num.Met.Heat Fluid Flow 26(2016)214.

[5]X.Si,X.Zhu,L.Zheng,X.Zhang,and P.Lin,Int.J.Heat Mass Transfer.92(2016)979.

[6]M.Y.Malik,M.Bibi,F.Khan,and T.Salahuddin,AIP Adv.6(2016)035101.

[7]M.G.Reddy,J.Eng.Phys.Thermophy.88(2015)240.

[8]M.Ghalambaza,A.Behseresht,J.Behseresht,and A.Chamkha,Adv.Powder Tech.26(2015)224.

[9]G.J.Li,J.Ma,and B.W.Li,J.Heat Transfer.137(2015)032701-1.

[10]I.L.Animasaun and N.Sandeep,Power Technol.301(2016)858.

[11]R.V.Williamson,Ind.Engr.Chem.Res.11(1929)1108.

[12]M.Y.Malik and T.Salahuddin,Int.J.Nonlinear Sci.Num.Sim.16(2015)161.

[13]M.Y.Malik,T.Salahuddin,A.Hussain,S.Bilal,and M.Awais,AIP Adv.5(2015)107227.

[14]T.Salahuddin,M.Y.Malik,A.Hussain,S.Bilal,and M.Awais,J.Mag.Mag.Mat.5:doi.org/10.1016/j.jmmm.2015.11.022(2015).

[15]T.Hayat,A.Shafiq,and A.Alsaedi,Alex.Engr J.55(2016)2229.

[16]B.C.Prasannakumara,B.J.Gireesha,R.S.R.Gorla,and M.R.Krishnamurthy,J.Aerosp.Eng.04016019:1-10(2016).

[17]T.Hayat,S.Bibi,M.Rafiq,A.Alsaedi,and F.M.Abbasi,J.Mag.Mag.Mat.page doi.org/10.1016/j.jmmm.2015.10.107(2015).

[18]M.M.BhattiandM.M.Rashidi,J.Mol.Liq.doi:10.1016/j.molliq.2016.05.049,(2016).

[19]T.Hayat,S.Qayyum,M.Imtiaz,and A.Alsaedi,PLOs ONE 11(2016)e0148662.

[20]T.Hayat,M.Imtiaz,A.Alsaedi,and S.Almezal,J.Mag.Mag.Mat.401(2016)296.

[21]J.V.R.Reddy,V.Sugunamma,and N.Sandeep,Int.J.Engr.Res.Africa 20(2016)130.

[22]S.Mansur,A.Ishak,and I.Pop,J.App.Fluid Mech.9(2016)1073.

[23]P.K.Kameswaran,S.Shaw,P.Sibanda,and P.V.S.N.Murthy,Int.J.Heat Mass Tran.57(2013)465.

[24]M.R.Eid,J.Mol.Liq.220(2016)718.

[25]W.Ibrahim,Prop.Power Res.5(2016)164.

[26]O.D.Makinde,T.Iskander,F.Mabood,W.A.Khan,and M.S.Tshehla,J.Mol.Liq.221(2016)778.

[27]H.Rosali,A.Ishak,R.Nazar,and I.Pop,Prop.Power Res.5(2016)118.

[28]F.Mabood,S.M.Ibrahim,M.M.Rashidi,M.S.Shadloo,and G.Lorenzini,Int.J.Heat Mass Tran.93(2016)674.

[29]T.R.Mahapatra and A.S.Gupta,Heat Mass Trans.38(2002)517.

[30]R.Nazar,N.Amin,D.Filip,and I.Pop,Int.J.Eng.Sci.42(2004)1241.

[31]M.Y.Malik and T.Salahuddin,Int.J.Nonlinear Sci.Num.Sim.16(2015)161.