Rheological Analysis of CNT Suspended Nano fluid with Variable Viscosity:Numerical Solution

Noreen Sher Akbarand Zafar Hayat Khan

1DBS&H,CEME,National University of Sciences and Technology,Islamabad,Pakistan

2Department of Mathematics,University of Malakand Dir(lower)Khyber Pakhtunkhwa,Pakistan

1 Introduction

In recent years,the research on flow over a stretching sheet has spawned important interest because of its copious manufacturing applications such as in the fabrication of canvas stuffover an extrusion progression,the conservation of bath,the boundary layer along corporeal administration conveyers,the sweptback extrusion of soft sheets crystal and polymer industries, fiber mechanized etc.Boundary layer deportment above a poignant unremitting solid exterior is a momentous sort of flow arising in abundant manufacturing processes.Sakiadis[1−2]was the first to examine the boundary layer flow over an incessant stretching surface.In this stare,Crane[3]premeditated flow over a stretching plate.Stagnation-point flow has been originated in frequent applications in industrialized and apparatus.It can be positioned in the stagnation region of flow fleeting with any shape of frame,i.e.,wharf and aerofoil. Hiemenz[4]showed that stagnation-point flow can be examined by the Navier–Stokes equations concluded with similarity solution in which the number of variables can be reduced by one or supplementary by a complement redecoration.For more detail see Refs.[5–10].

Fluids in association with heat transfer used in preeminence compeers,substance production,microelectronics cooling,air-conditioning,refrigeration,transportation,and several other applications.It is required to enhance effective thermal conductivity of the fluids to increase heat transfer rate.After Choi,[11]it has been proved experimentally and theoretically by many researchers[12−18]that flush with small solid volume fraction of nanoparticles i.e.,less than 5 percent,the thermal conductivity of heat transfer fluids can be enhanced by 10–50%.Carbon nanotubes,a form of fullerene,obligate imminent in fields such as nanotechnology,optics,electronics,architecture,and materials science.In recent years new solicitations have taken benefit of their sole electrical properties,unexpected strength,and competence in heat conduction.An experimental investigation was conducted by Kim and Peterson[19]to explore the effect of the morphology of carbon nanotubes on the thermal conductivity of suspensions.According to them the tremendous enrichment for the SWNT rebellious to a volume fraction of 1.0%approached 10%,which was sensible to be redundant than twofold that of the other values,3.5%,attained in the case of aluminum oxide nano fluids.The heat transfer nanofluids encompass carbon nanotubes(CNT’s)and magnetic- field delicate nanoparticles of Fe2O3 reported by Hong et al.[20]They pragmatic that on lengthier possessions in compelling field,the particles slowly move and form large bunches of particles,producing clomping of CNT’s,and then declining the thermal conductivity.Kamali and Binesh[21]examined numerically the convective heat transfer of multi-wall carbon nanotubes(MWCNT)with constant wall heat flux stipulation.They deciphered Navier stokes equations by the finite volume method using CNT-based nano fluids using power law model.They pragmatic that the heat transfer coefficient is subjugated by the wall region because of non-Newtonian behavior of CNT nano fluid.Very recently Khan et al.[22]studied homogeneous fluid model to analyze the flow and heat transfer of carbon nanotubes(CNT’s)with Navier slip and constant heat flux boundary conditions.Further recent literature can be viewed through Refs.[23–30].

The aim of the present article is to discuss the twodimensional stagnation-point flow of carbon nanotubes towards a stretching sheet with water as the base fluid under the influence temperature dependent viscosity.Similarity transformations are used to simplify the governing boundary layer equations for nanofluid.This is the first article on the stagnation point flow of CNTs over a stretching sheet with variable viscosity.A well known Reynold model of viscosity is used.Single wall CNTs are used with water as a base fluid.The resulting nonlinear coupled equations with the relevant boundary conditions are solved numerically using shooting method.The influence of the flow parameters on the dimensionless velocity,temperature,skin friction,and Nusselt numbers are explored and presented in forms of graphs and interpreted physically.

2 Formulation of the Problem

We consider the two-dimensional stagnation-point flow over a stretching sheet with water as based fluids encompassing single-wall CNT’s.The flow is presumed to be laminar,steady,and incompressible.The base fluid and the CNT’s are expected to be in updraft equilibrium.Sheet is assumed to be stretched with the different velocityuw,vwalong thex-axis andy-axis respectively.Further,we have taken the constant temperatureTwat wall and the ambient temperatureT∞.Fluid viscosity is considered to be temperature dependent.(see Fig.1)

Fig.1 Geometry of the problem(a)Shrinking case(b)Stretching case.

With the above analysis the boundary layer equations for the proposed model can be written as follows

The relevant boundary conditions are of the form

In above equationsuandvare the velocity components along thex-andy-axes,respectively,a,c＞0 the constant,uwis velocity at wall,Tis the temperature,ρnfis the nano fluid density,µnfis the viscosity of nanofluid andαnfis the thermal diffiusivity of nano fluid defined as[28]

whereµfis the viscosity of base fluid,ϕis the nanoparticle fraction,(ρCp)nfis the effective heat capacity of a nanoparticle,knfis the thermal conductivity of nano fluid,kfandkCNTare the thermal conductivities of the base fluid and carbon nano tubes,respectively,ρfandρCNTare the thermal conductivities of the base fluid and carbon nano tubes,respectively.

Introducing the following similarity transformations

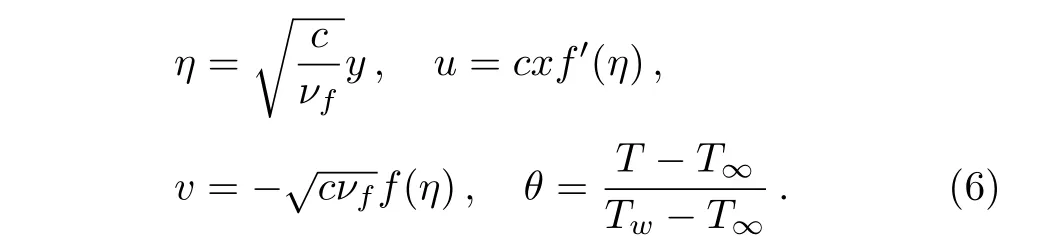
Making use of Eqs.(5)–(6)in Eq.(1)to Eq.(4),we have

wherePr=(µCp)f/kfis the Prandtl number andS=a/cstagnation parameter.

Reynolds model of viscosity expression can be taken as[18]

whereαis the viscosity parameter.

Expressions for the skin-friction coefficient and the local Nusselt numberNuare

Dimensionless form of Eq.(11)takes the form

3 Numerical Illustration

Numerical solutions to the governing ordinary differential equations(7)–(8)with the boundary conditions(9)were obtained using a shooting method.First we have converted the boundary value problem(BVP)into initial value problem(IVP)and assumed a suitable finite value for the far field boundary condition,i.e.η→ ∞,sayη∞.To solve the IVP,the values forf′′(0)andθ′(0)are needed but no such values are given prior to the computation.The initial guess values off′′(0)andθ′(0)are chosen and fourth order Runge–Kutta method is applied to obtain a solution.We compare the calculated values off′(η)andθ(η)at the far field boundary conditionη∞(=20)with the given boundary conditions(9b)and the values off′′(0)andθ′(0)are adjusted using Secant method for better approximation.The step-size is taken as Δη=0.01 and accuracy to the fifth decimal place as the criterion of convergence.It is important to note that the dual solutions are obtained by setting two different initial guesses for the values off′′(0).

4 Graphical Results and Discussion

The influence of the flow parameters on the dimensionless velocity,temperature,skin friction,Nusselt numbers and streamlines are presented in Figs.2–7.Figures 2(a)–2(c)show the variation of velocity pro file for different values of nanoparticle volume fraction with Hartmann numberM,Viscosity parameterα,Grash of numberGr.Since Hartmann numberMis the ratio of electromagnetic force to the viscous force and magnetic field is applied in the opposite direction of the fluid so with the increase in Hartmann number causes increase in electromagnetic force that increases velocity pro file and boundary layer thickness for assisting flow but decreases velocity pro file for opposing flow.Viscosity parameterαshows the same behavior on velocity pro file as we are considering temperature dependent viscosity so when rises temperature dependent viscosity, fluid resistance becomes slow and the fluid moves speedily so when we increases viscosity parameterαvelocity field increases rapidly and boundary layer thickness also increases(see Fig.2(b)).Figure 2(c)shows that when we increase Grash of numberGr(the ratio of the buoyancy to viscous force acting on a fluid),then there will be more buoyancy forces,that causes increase in velocity field and boundary layer thickness.It is also seen that for each case with the increase in solid volume fraction of nanoparticles velocity pro file increases for assisting flow but decreases for opposing flow.

Fig.2 Variation of velocity pro file for different values of nanoparticle volume fraction with(a)Hartmann number M.(b)Viscosity parameter α.(c)Grash of number Gr.

Fig.3 Variation of temperature pro file for different values of nano particle volume fraction for assisting and opposing flow with Hartmann number M.

Fig.4 Variation of temperature pro file for different values of nano particle volume fraction for assisting and opposing flow with viscosity parameter α.

Figure 3(a)to Fig.5(b)show the temperature profile for different values of nanoparticle volume fraction with Hartmann numberM,Viscosity parameterα,and Grash of numberGr,it is seen that when we increase Hartmann number causes increase in electromagnetic force that increases temperature pro file and thermal boundary layer thickness also increases for assisting as well as for opposing flow(see Figs.3(a)and 3(b)).Viscosity parameterαshows the same behavior on temperature pro file as we are considering temperature dependent viscosity so when rises temperature dependent viscosity, fluid resistance becomes slow and the fluid moves speedily so when we increase viscosity parameterαtemperature field increases rapidly and thermal boundary layer thickness also increases(see Figs.4(a)and 4(b)).Figures 5(a)and 5(b)show that when we increase Grash of number Gr(the ratio of the buoyancy to viscous force acting on a fluid),then there will be more buoyancy forces,that cause increase in temperature pro file and thermal boundary layer thickness also increases.It is also observed that for each case with the increase in solid volume fraction of nanoparticles temperature pro file increases for both assisting and opposing flow.

Variation of skin-friction coefficient for assisting and opposing flow with Grash of number Gr,Hartmann numberM,Viscosity parameterαare presented in Figs.6(a)–6(c).Figure 6(a)shows that when we increase Grash of numberGr(the ratio of the buoyancy to viscous force acting on a fluid),then there will be more buoyancy forces it causes increase in skin friction coefficient for SWCNT for assisting flow but decreases for opposing flow.It is seen that with the increase inMelectromagnetic force are high as compare to viscous force skin friction coeffi-cient decreases for SWCNT for assisting flow but increases for opposing flow,similar behavior is observed for viscosity parameterα,rise in viscosity parameterαskin friction coefficient decreases for SWCNT for assisting flow but increases for opposing flow.

Variation of Nusselt number for assisting and opposing flow with Grashof numberGr,Hartmann numberM,Viscosity parameterαare presented in Figs.7(a)–7(c).Figure 7(a)shows that when we increase Grash of numberGr(the ratio of the buoyancy to viscous force acting on a fluid),then there will be more buoyancy forces it causes decrease in Nusselt number for SWCNT for assisting flow but increases for opposing flow.It is seen that with the increase inMelectromagnetic force are high as compare to viscous force Nusselt number increases for SWCNT for assisting flow but decreases for opposing flow,opposite behavior is observed for viscosity parameterα,rise in viscosity parameterα,Nusselt number decreases for SWCNT for assisting flow but increases for opposing flow.

Table 1 presents thermo physical properties of different base fluid and CNT’s.Table 2 gives the numerical values of skin friction(assisting flow)for water functionalized SWCNT nanoparticle with the various values of flow parameters.Table 3 gives numerical values of Nusselt number(assisting flow)for water functionalized SWCNT nanoparticle with the various values of flow parameter.Table 4 gives the comparison of present results with the existing literature.

Fig.5 Variation of temperature pro file for different values of nano particle volume fraction for assisting and opposing flow with Grashof number Gr.

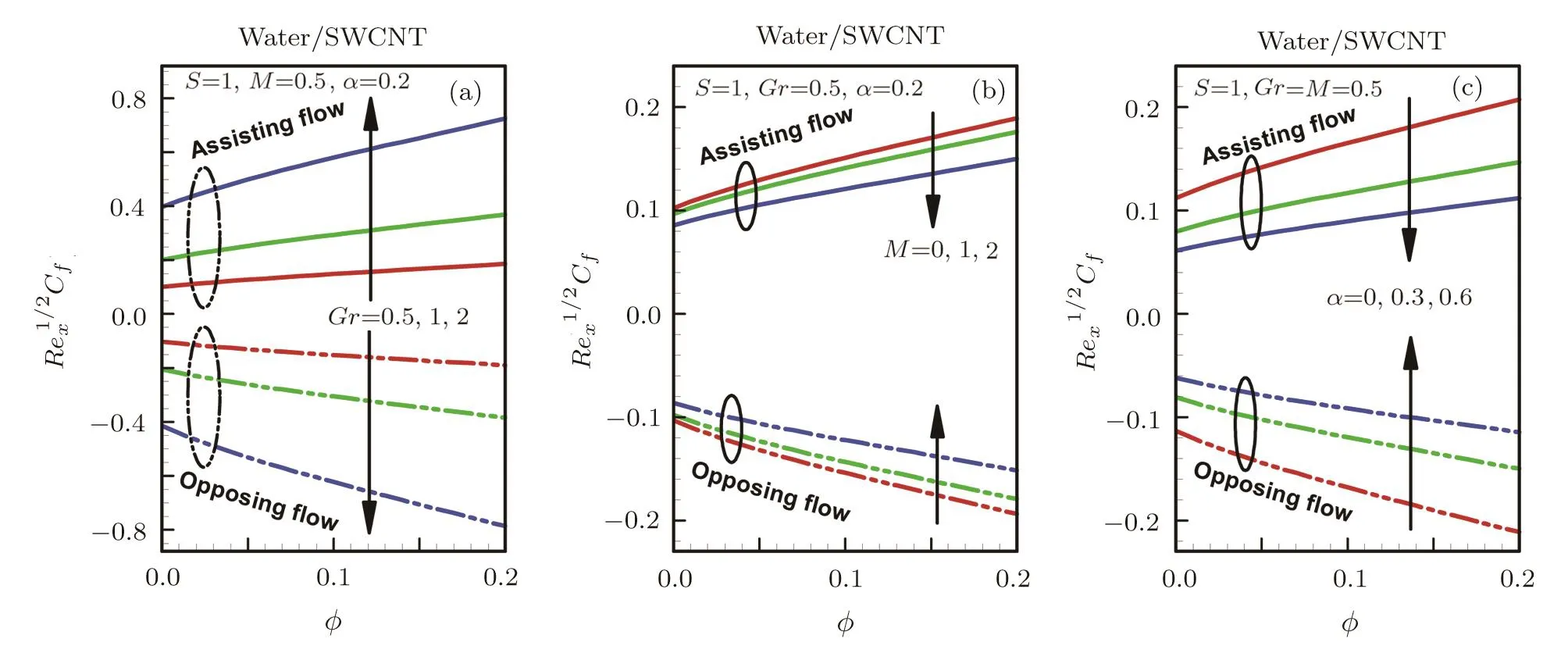
Fig.6 Variation of skin-friction coefficient for assisting and opposing flow with(a)Grash of number Gr.(b)Hartmann number M.(c)Viscosity parameter α.

Table 1 Thermal properties of base fluid(water)and nanoparticles.

Fig.7 Variation of local Nusselt number for assisting and opposing flow with(a)Grash of number Gr.(b)Hartmann number M.(c)Viscosity parameter α.

Table 2 Numerical values of skin friction(assisting flow)for water functionalized SWCNT nanoparticle with the various values of M,α,and Gr with S=1.

Table 3 Numerical values of Nusselt number(opposing flow)for water functionalized SWCNT nanoparticle with the various values of M,α,and Gr with S=1.0.

Table 4 Comparison of results for the reduced Nusselt number for pure fluid.

5 Conclusion

Two-dimensional stagnation point flow for single wall carbon nanotubes suspended water towards a stretching sheet under the influence of temperature dependent viscosity is discussed.Main conclusion is drawn as follows:

(i)The increase in Hartmann numberMcauses increase in electromagnetic force that increases velocity profile and boundary layer thickness for assisting flow but decreases velocity pro file for opposing flow.

(ii)When rises temperature dependent viscosity, fluid resistance becomes slow and the fluid moves speedily so when we increase viscosity parameterαvelocity field increases rapidly and boundary layer thickness also increases.

(iii)Increase in Grash of numberGrcauses increase in velocity field and boundary layer thickness.

(iv)It is also seen that for each case with the increase in solid volume fraction of nanoparticles velocity pro file increases for assisting flow but decreases for opposing flow.

(v)Increase in viscosity parameterαtemperature field increases rapidly and thermal boundary layer thickness also increases.

(vi)It is also observed that for each case with the increase in solid volume fraction of nanoparticles temperature pro file increases for both assisting and opposing flow.

(vii)It is seen that with the increase inMelectromagnetic force are high as compare to viscous force skin friction coefficient decreases for SWCNT for assisting flow but increases for opposing flow.

(viii)When we increase Grashof numberGrcauses decrease in Nusselt number for SWCNT for assisting flow but increases for opposing flow.

(ix)It is seen that with the increase inMelectromagnetic force are high as compare to viscous force Nusselt number increases for SWCNT for assisting flow.

References

[1]B.C.Sakiadis,J.American Instit.Chem.Eng.7(1961)221.

[2]B.C.Sakiadis,J.American Instit.Chem.Eng.7(1961)26.

[3]L.Crane,Zeitschrift Für Angewandte Mathematik und Physik 21(1970)645.

[4]K.Hiemenz,Dinglers Polytechnisches Journal 326(1911)321.

[5]A.Ishak,R.Nazar,and I.Pop,Comput.Math.Appl.56(2008)3188.

[6]A.Ishak,R.Nazar,and I.Pop,Nonlinear Anal.RWA 10(2009)2909.

[7]F.Labropulua and I.Pop,Int.J.Thermal Sci.49(2010)1042.

[8]T.R.Mahapatra,S.K.Nandy,K.Vajravelu,and R.A.Van Gorder,Meccanica.47(2012)1623.

[9]Noreen Sher Akbar,S.Nadeem,Rizwan Ul Haq,and Z.H.Khan,Indian J.Phys.87(2013)1121.

[10]S.Nadeem,Int.J.of Heat and Mass Transfer 57(2013)679.

[11]S.U.S.Choi,ASME Fluids Engng.Div.231(1995)99.

[12]A.Ebaid,Hasan A.El-arabawy,and Y.Nader,Int.J.Differential Equations Volume(2013),Article ID 865464,1-8 pages.

[13]E.H.Aly and A.Ebaid,J.Comput.Theor.Nanosci.10(2013)2591.

[14]Noreen Sher Akbar,S.Nadeem,Rizwan Ul Haq,and Z.H.Khan,Chinese Journal of Aeronautics 26(2013)1389.

[15]E.H.Aly and A.Ebaid,J.Comput.Theor.Nanosci.10(2013)2591.

[16]S.Nadeem and S.T.Hussain,Appl.Math.Mech.35(2014)489.

[17]M.Sheikholeslami,R.Ellahi,H.R.Ashorynejad,and G.Domairry,J.Comput.Theor.Nanosci.11(2014)486.

[18]R.Ellahi,M.Raza,and K.Vafai,Math.Comput.Mode.55(2012)1876.

[19]B.H.Kim and G.P.Peterson,J.Therm.Phys.Heat Transf.3(2007)451.

[20]H.Hong,B.Wright,J.Wensel,S.Jin,X.Rong Ye,and W.Roy,Synthetic Metals 157(2007)437.

[21]R.Kamali and A.Binesh,Int.Commun.Heat Mass Transf.37(2010)1153.

[22]W.A.Khan,Z.H.Khan,and M.Rahi,Appl Nanosci 4(2014)633.

[23]A.Ebaid,Emad H.Aly,and N.Y.Abdelazem,J.Appl.Math.Inf.Sci.8(2014)1639.

[24]W.A.Khan and I.Pop,Int.J.Heat Mass.Transfer 53(2010)2477.

[25]C.Y.Wang,J.Appl.Math.Mech.(ZAMM)69(1989)418.

[26]R.S.R.Gorla and I.Sidawi,Appl.Sci.Res.52(1994)247.

[27]N.Bhaskar Reddy,T.Poornima,and P.Sreenivasulu,International Journal of Engineering Mathematics Volume(2014)Article ID 905158,1-10 pages.

[28]S.Nadeem and S.Ijaz,AIP Adv.5(2015)107217.

[29]S.T.Hussain,R.Haq,and S.Nadeem,J.Mol.Liq.214(2016)136.

[30]R.Ellahi,IEEE Trans.Nanotechnol.14(2015)726.