用MC算法优化基于SPH的海浪粒子模型
2017-05-12刘文龙
刘文龙,张 静
(1.中国地震局第一监测中心,天津 300180;2.山东科技大学 测绘科学与工程学院,山东 青岛 266510)
用MC算法优化基于SPH的海浪粒子模型
刘文龙1,张 静2
(1.中国地震局第一监测中心,天津 300180;2.山东科技大学 测绘科学与工程学院,山东 青岛 266510)
结合风浪场复杂的动力学、时空特性以及对目前海浪仿真方法的研究总结,针对海浪仿真模拟中存在的真实感不足,难以模拟海浪破碎等问题,根据流体的物理特性,采用光滑粒子流体动力学(SPH)的方法实现了海浪的动态演变仿真。然后针对基于SPH方法的海浪粒子模型存在的离散性和真实感较差的问题,采用一种基于移动立方体法(MC)的海浪运动的自由表面抽取算法,完成了海浪场的表面建模,优化了基于粒子系统的海浪模拟效果。实验表明,用MC算法优化的方法既满足了海浪动态演变的仿真要求,又使水体模型更加连贯,更接近真实水体效果,优化效果较为明显,是综合利用体绘制与面绘制法实现三维可视化模拟的一次成功的探索。
海浪模拟;光滑粒子流体动力学;移动立方体法
海浪仿真是近些年来计算机图形学领域研究的热点之一,它在虚拟现实应用、计算机游戏以及电影制作中起着重要的作用[1]。另外,海浪的仿真模拟是构建海洋环境信息可视化平台的一个重要组成部分,平台的建立可显著提高我国海洋信息的可视化水平。
海浪具有复杂的动力学、时空特性,对其三维模拟有着特殊的要求,这使得海浪建模及绘制成为海浪仿真模拟中的难点。海浪建模的本质是海浪的真实感绘制,它是海洋环境仿真的基础,在很大程度上决定了仿真效果的好坏[2]。针对海浪复杂的特性,本文在基于粒子的拉格朗日法(SPH方法)建立的海浪粒子模型基础上采用移动立方体(MC算法)算法对海浪粒子表面建模,在海浪动态演变的连贯性方面做出改进,形成更为逼真的海浪动态演变效果。
1 基于SPH的海浪建模
SPH方法是一种由一组粒子代替流体获得流体动力学公式的近似数学解决方案的方法[3],该方法的基本思想是将连续的流体(或固体)用相互作用的质点组来描述[4],各个物质点上承载各种物理量,包括质量、速度等,通过求解质点组的动力学方程和跟踪每个质点的运动轨道,求得整个系统的力学行为。
SPH方法是一种纯Lagrange方法,能避免Euler描述中欧拉网格与材料的界面问题,特别适合于求解高速碰撞等动态大变形问题[5]。因此,SPH是一种适合于三维流体的模拟方法。采用SPH方法进行海浪建模时必须首先将其粒子化。这些海浪粒子在仿真初始的时候给定,所有的粒子都使用统一的光滑核半径,而且都具有质量、密度、速度、加速度、位置等属性,这些属性在模拟仿真过程中会不断地发生变化。
本文在.NET环境下利用OpenGL设计并实现一个粒子系统。SPH海浪运动模拟主要包括以下3个方面分析建立海浪运动模型。
(1)初始化粒子的属性,生成基本的海浪粒子类;
(2)分析海浪粒子受力情况,计算粒子速度、加速度等属性的变化,模拟海浪的运动状态;
(3)计算粒子位置,判断是否会与周围环境障碍物发生碰撞;若发生了,重新计算粒子加速度、速度等变量,以确定粒子碰撞后的位置。图1为渲染效果图。

图1 SPH渲染效果
2 基于MC的粒子群表面建模
由于SPH方法的局限性,从基于SPH方法的海浪粒子系统的模拟中可以看出海浪模型只是一堆离散的水粒子,流动水体的连贯性和真实感较差。针对此问题,提出了一种基于移动立方体法(MC算法)的海浪运动的自由表面抽取算法,对海浪场的表面建模。
MC算法是应用最广泛的等值面方法,其研究主要集中在算法的改进和算法在不同领域的应用上。MC算法在三维流体可视化中的应用己成为计算机图形学中一个重要研究热点[6]。MC算法的不断完善和发展,使得提供直观、逼真而且能够包含原始信息中隐含的丰富的三维信息成为可能。在混合流和多相流的模拟中,不同流体间的界面绘制极其重要,利用Ma方法来进行绘制将成为一个广泛的应用方法。将计算流体力学的数值方法MC方法结合起来完成对流体三维可视化的模拟对分析结果的准确性和正确性有深远意义,并促进了应用领域的发展[7]。
密度是海浪粒子的一个重要属性,通过比较密度值的大小可确定海浪与大气环境之间的交界面,即海浪的自由运动表面,这在海浪仿真模拟中起着重要的作用。本文采用MC算法从海浪密度场中提取海浪表面,主要包括下面几个方面的内容。
2.1 基于立体网格的密度场数据采样
根据粒子的空间分布建立三维空间网格,将立体网格的节点作为海浪场的采样点,生成规则分布的海浪密度场数据。网格节点的密度值可以通过SPH密度插值公式来计算。SPH方法核心是核函数,它表示在一定的光滑长度范围内其它临近粒子质点对研究粒子影响程度的权函数。假设流体中某点r,在光滑核半径h范围内受数个粒子影响,其位置分别是r0,r1,r2…,rj,该点位置处某项属性A的累加值就可以用式(1)来表示。

式中:Aj是要累加的某种属性,mj和ρj是周围粒子的质量和密度;rj是该粒子的位置,h是光滑核半径;函数W为光滑核函数。
根据式(1),用密度ρ代替式中的A,可以得到密度的计算公式:

网格节点的密度值计算使用的光滑核函数为Poly6函数,所有网格的质量相同且都为m,在三维情况下,ri处的密度计算公式可表示为:
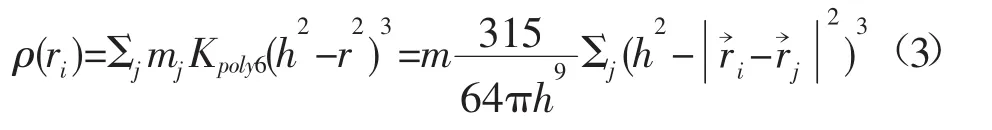
2.2 基于MC算法的密度等值面提取
MC算法的基本思想是将整个三维数据所在空间按照一定的规则划分成一个个体元,立方体元8个顶点都拥有自己的函数值,根据给定的阈值对体元12条边进行插值,构造体元内部的三角面片,连接所有体元的三角面片完成等值面的提取。
在离散的三维空间数据场中,通过每次读取连续两张切片数据形成一个层,两张切片上下相对应的8个点构成一个立方体体元,其中体元各顶点具有自己的属性值。这样整个三维空间可以视为由多个拥有顶点值的规则体元构成,如图2所示为三维规则数据场与体元。在MC算法中,需要给定一个等值面的阈值,将阈值依次与体元的8个顶点作比较,根据比较结果将各顶点标记为内部和外部两种状态,可以理解为二进制值0和1。如果一条边的两个顶点分别属于这两种情况,则说明这条边与等值面有交点。

图2 三维空间数据场及体元
由于每个体元的8个顶点分别可能具有两种状态,因此每个体元进行比较后有28=256种情况。经过分析,这256种情况存在对称性。如果将一个体元顶点的两种状态互换后,等值面的连接是不变的(如图3(a)),根据体元的这种互补对称性,256种不同情况的种类将减少到32种。另外,体元8个顶点存在旋转对称性,即旋转立方体体元后,许多情况是同构的(如图3(b)),这样将不同情况进一步组合,可以减少到16种情况,这16种情况包括所有顶点均在等值面内与均在等值面外两种,这两种情况下体元12条边与等值面均无交点,拓扑结构一致,可以合并为一种情况。
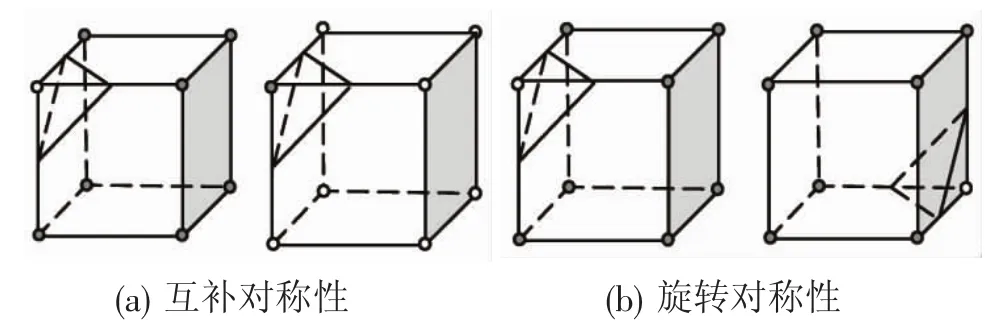
图3 互补对称性与旋转对称性
经过合并后15种情况如图4所示,把这15种基本的情况经旋转,倒置后可以得到完整的256种情况。

图4 体元插值的15种基本情况
基于上面的分析,在实现方法上,可以由立方体体元的8个顶点的内部和外部两种情况得到一个0~255之间的索引值,如图5所示,MC方法用一个字节的空间构造了一个体元的状态表,表中每一位代表相应顶点的状态(0或者1)。根据这个索引表和体元的互补对称性与正反对称性,可以知道体元属于图4中的哪一种情况,以及等值面与体元哪条边相交。

图5 体元顶点状态表

式中:V代表所求交点的位置坐标;V0,V1代表体元边界的两个顶点坐标;C代表给定的阈值,Value0与Value1代表体元边界两个顶点的函数值。
采用MC算法从海浪密度场中抽取海浪表面,首先须确定海浪表面的密度值,以此密度值作为MC算法中插值用的阈值。然后根据MC算法原理,将每个体元8个顶点的密度值与水面密度值进行比较,确定出与阈值有交点的体元边界;通过线性插值,计算阈值与体元边界交点的坐标值,并利用中心差分法求体元顶点处的法向量,然后同样利用线性插值方法求出三角面片顶点处的法向量;最后根据三角面片的顶点坐标及法向量绘制等值面,完成海浪表面的提取。
首先,根据体元与等值面相交的256种情况构建状态表。此表包括索引、指向256种相交边情况的指针以及三角剖分模式。其中,索引指的是标记8个顶点状态的有序二进制编码。
然后,确定海浪粒子群的空间范围,构造立方体体元。通过遍历所有海浪粒子获取粒子三维坐标位置的最大最小值,然后设定立方体体元的边长,划分体元并为各体元8个顶点赋坐标值。其中,体
在确定等值面与体元的相交状态后,需要计算构造的三角面片顶点的位置。当三维离散数据场的密度较高,即体元很小时,可以假设函数值沿着体元的边界呈线性变化。所以,等值面与体元边的交点可以通过线性插值来求得,如(4)式所示。元的存储结构为:
struct gridcell
{
//存储体元八个顶点坐标的Vector3DF类型数组
Vector3DF v[8];
//存储体元八个顶点法向量值的Vector3DF类型数组
Vector3DF n[8];
//存储体元八个顶点密度值的double类型数组
double val[8];
};
第三步,在划分体元后,计算体元各顶点的函数值,即密度值。密度值的计算可通过式(3)密度计算公式得到,具体的计算方法同海浪粒子的密度计算。
第四步,比较体元每个顶点的密度值与给定的等值面值,若顶点密度值大于给定阈值,赋值为0,否则赋值为1,这样会构造一个表示顶点与阈值之间关系的二进制值。比如:10111111表示顶点V6的值大于给定的等值面值。
第五步,查找构造的状态表,得到一个代表与体元边界有交点的二进制值。例如第四步中根据顶点的二进制值查到状态表得到的代表相交边状态的二进制值为:010001100000,它表示与边5、6、10有交点。见立方体体元示意图6。

图6 立方体体元示意图
第六步,通过线性插值方法,计算体元边界与海浪密度等值面的交点坐标;利用中心差分方法,计算体元各顶点处的法向,然后通过线性插值方法,求得所构造的三角面片各顶点处的法向量。
最后,利用OpenGL中的glBegin(GL_TRIANGLES)三角面片绘制方法,根据插值得到的各三角面片的顶点坐标值以及法向量绘制等值面图像。
3 模拟效果对比
采用MC算法优化的基于SPH方法的海浪流动模型实现方法综合了SPH方法适合与求解高速碰撞等动态大变形问题的优点,弥补了该方法粒子性强、连贯性差的缺点,相比单一的SPH方法构建的海浪流动模拟效果连贯性更好,更符合流动的海浪的状态,如图7所示,SPH法较好地模拟了海浪碰撞效果,但是渲染效果粒子感较强,没有形成连贯的水体模型;采用MC法优化的方法既保留了海浪碰撞效果,又使水体模型更加连贯,更接近真实水体效果,优化效果较为明显。

图7 SPH与MC优化后的渲染效果对比
4 总结
结合海浪基本特征,利用物理模型与粒子系统相结合的方法—SPH方法完成了对海浪流动的模拟,然后用MC算法对海浪粒子模型进行了表面建模,使海浪模型更具有连贯性,效果更为逼真。将流体力学数值计算法与MC法结合起来完成了流动海浪的三维可视化模拟,是综合利用体绘制与面绘制法实现三维可视化模拟的一次成功的探索。
存在问题:MC算法改进的基于SPH的海浪模拟并没有脱离粒子系统,因此在场景较大,粒子数目增多后,模拟的实时性会较差。这可能需要考虑到GPU加速等技术。所以该模拟系统还有很多方面需要进一步研究与改进。
参考文献:
[1]张静.基于粒子系统的海浪动态演变模拟仿真研究[D].青岛:山东科技大学,2012.
[2]丁绍洁.虚拟海洋环境生成及场景特效研究[D].哈尔滨:哈尔滨工程大学,2008.
[3]高峰.基于SPH的化学溶液倾倒过程仿真[D].长春:东北师范大学,2010.
[4]钟子春.实时流体交互性模拟算法的研究与实现[D].成都:电子科技大学,2009
[5]陆慧莲.基于LS-DYNA和HyperMesh的某型飞机垂尾前缘鸟撞分析[J].航空工程进展,2013,4(4):498-502.
[6]叶再春.MC算法研究及在三维流体可视化模拟中的应用[D].苏州:苏州大学,2009.
[7]矫春海.基于改进MC算法的医学图像三维重建研究[J].微型机与应用,2011,30(3):39-45.
Optimization of the Wave Particle Mode Based on SPH by the MC Algorithm
LIU Wen-long1,ZHANG Jing2
1.First Crust Deformation Monitoring and Application Center,CEA,Tianjin 300180,China; 2.College of Geosciences and Technology,Shandong University of Science and Technology,Qingdao 266510,Shandong Province, China
Combined with the complex dynamics,spatial and temporal characteristics of the wave field and research of wave simulation methods,and in order to solve the problem of the lack of realistic rendering in wave simulation,and difficulty to simulate wave breaking and other issues,this paper realizes the simulation of dynamic evolution of the ocean waves by adopting the SPH method based on the physical characteristics of the fluid.In view of the discreteness and the poor realistic rendering in wave particle model based on the smoothed particle hydrodynamics method,this paper uses a free surface extraction algorithm based on the marching cubes algorithm,and completes surface modeling of the wave field,while optimizing the ocean wave effect based on particle system.The results can meet the requirements of simulating dynamic evolution of ocean waves with optimized MC algorithm,and the water model is more fluent and closer to the effects of real water bodies.The results proposed in this paper is a successful exploration of the comprehensive utilization of volume rendering and surface rendering method to realize 3D visual simulation.
wave simulation;SPH;marching cubes method
P731;TP391.9
A
1003-2029(2017)02-0041-05
10.3969/j.issn.1003-2029.2017.02.007
2016-05-19
刘文龙(1987-)男,硕士,主要研究方向为地理信息系统。E-mail:liuwenlon1987@126.com
