基于船舶空气流场仿真的船舶测风偏差校正方法
2017-05-12漆随平郭颜萍王东明
胡 桐,漆随平,郭颜萍,王东明
(山东省海洋环境监测技术重点实验室,山东省科学院海洋仪器仪表研究所,国家海洋监测设备工程技术研究中心,山东 青岛 266001)
基于船舶空气流场仿真的船舶测风偏差校正方法
胡 桐,漆随平,郭颜萍,王东明
(山东省海洋环境监测技术重点实验室,山东省科学院海洋仪器仪表研究所,国家海洋监测设备工程技术研究中心,山东 青岛 266001)
船舶海面风观测易受船体和上层建筑造成的畸变气流影响,使测风数据存在偏差。针对船舶相对风测量偏差校正问题,采用CFD仿真方法研究船体周围钝体绕流气流场,量化桅杆左、右横桁实测相对风速、风向与舰桥上部参考测风点相对风速、风向偏差,利用最小二乘支持向量机分别对左、右舷测风偏差进行回归并建立校正模型。通过海上实船实验采集桅杆左、右横桁与舰桥上部测风点处的相对风测量数据,验证模型校正测风偏差的实际效果,结果表明CFD仿真建模方法能够有效降低实验船型56%的相对风速测量偏差。
舰船空气流场;CFD;风测量;偏差校正
海气动量、热量、水汽交换过程中,海面风几乎起主导作用。现场实测海面风速、风向资料大部分由船舶、浮标、岸站等常规观测系统获取。船舶作为海面气象要素的重要观测手段,提供了长期并且持续的海面风观测记录。船载测风传感器测量的是相对风,真风通过相对风、航速和航向进行解算。但移动平台测风的固有特点会造成相对风观测数据中存在偏差,原因包括:
(1)船体、上层建筑对气流的遮挡。经过测风点的气流实际上已经受到船体和上层建筑遮挡而产生了畸变[1],速度和方向与自由来流存在差别。风速、风向测量值与海面自由来流真实值之间的偏差直接影响海面摩擦速度u*和阻力系数CD10N的计算。当u10N为10 m/s时,10%的风速偏差将造成约27%的动量通量估计偏差[2]。
(2)船体摇摆的影响。船舶航行过程中受风、浪、流的综合作用产生纵摇、横摇和升沉,船体对周围气流场存在作用力,干扰相对风测量[3-4],并且对采用涡动相关法(Eddy Covariance)计算海气通量具有较为明显的影响[5-6]。
以上测风偏差与测风传感器本身的测量精度无关,提高传感器测量精度并不能消除偏差。实际上,船舶测风易受干扰的问题由来已久[7],气流在船体和上层建筑周围产生钝体绕流使船体周围气流场形态发生变化。世界气象组织规定测风传感器应安装于船上开阔位置,尽量靠近安装平台前部并具有一定高度[8]。由于无法将测风传感器安装到距离船体或上层建筑足够远的位置,传感器测量的是测风点处受干扰气流的速度和方向[9],有必要对测风偏差进行校正。
目前,计算流体力学(ComputationalFluidDynamics, CFD)仿真已被广泛应用于气流场分析与相关研究领域[10]。Yelland等指出测风点处气流速度与自由来流速度的比值在5~25 m/s范围内近似为常数[9]。Dupius等利用CFD仿真数据校正海面阻力系数CD10N[11]。Popinet等指出风速偏差独立于雷诺数而依赖于相对风向[12]。Moat等指出舰桥上部气流场形态在雷诺数 2×105~1×107范围内无显著差异[13-14]。Griessbaum指出测风偏差影响数值模式参数化方案,会导致气体输运速度kg有30%~50%的偏差[15]。O’Sullivan等指出校正测风偏差需要更多不同迎风角度的仿真数据[16]。Polsky分析了舰载机起降平台上的湍流扰动[17]。Wnęk等对LNG船风载荷进行评估并验证了CFD仿真结果的一致性[18]。贺少华等[19]对载机舰船气流场相关研究现状进行了综述。王伟[20]、赵永振[21]研究了不同船型上层建筑布局对气流场的影响。郜冶等对护卫舰船体周围气流场进行了数值模拟[22]。姜治芳等在舰船气流场研究方面做了大量工作[23-24]。上述研究工作针对不同问题,对船体周围钝体绕流流场进行了仿真计算,但未涉及海面风测量偏差的建模与校正。
本文采用CFD仿真方法研究某实验船船体周围钝体绕流气流场的分布情况,利用最小二乘支持向量机 (Least Square Support Vector Machine,LSSVM)对不同迎风角度条件下的风速、风向偏差进行回归建模,通过海上实船实验采集不同测风点的风速、风向数据,验证了该方法校正测风偏差的实际效果。
1 数值仿真
采用隐式修正SIMPLE算法求解三维不可压缩流体RANS方程和RNG k-epsilon两方程湍流模型,通过CFD仿真结果研究某型船钝体绕流气流场,利用LSSVM建立测风偏差校正模型。
1.1 几何模型与网格划分
以某实验船为例建立全尺寸三维几何模型,将特征长度小于7‰船长并且对气流影响小的船体、上层建筑和桅杆附体进行删减,包括围栏、支架、天线等,仅保留对气流场存在显著遮挡的大尺度几何特征。处理后的三维船体几何模型呈左右舷对称。计算域采用圆柱体形式,船舶三维几何模型置于计算域底面中心,底面半径为3.9倍船长,高度为1.6倍船长,计算域入口和出口分别由圆柱体侧面的1/ 2构成(如图1所示)。整个计算域阻塞比小于3%。

图1 计算域尺寸
采用非结构化四面体网格对计算域进行网格划分,对上层建筑和桅杆区域进行了网格加密以保证网格质量。在入口风速为5 m/s工况下,设置边界层第一层网格高度为3 mm,以满足湍流模型计算所使用标准壁面函数的y+条件。各工况下y+值范围为30~100。

图2 网格无关性检验
为检验网格无关性,在桅杆左、右横桁与舰桥上部分别设置半径为1 m的球形区域,观察流经以上3个区域气流的平均速度和方向。桅杆左、右横桁对应于实际的测风传感器安装位置,舰桥上部对应于海上实船实验安装的参考测风传感器位置(以下称参考测风点)。图2为船体正面迎风(海平面10 m高度风速设置为5 m/s)时,3个区域的平均风速变化情况。当网格数量达到360万,关注区域平均风速基本不随网格数量变化,因此选取360万网格进行各工况的CFD仿真。船体周围区域的局部网格如图3所示。

图3 船体周围面网格示意图
1.2 仿真参数设置
在相同迎风角度条件下,船体周围钝体绕流气流场形态在雷诺数2×105~1×107范围内无显著差异[13],经过测风点处的气流与自由来流的流速比值基本不变。本文采用相同的入口风速对不同迎风角度工况进行仿真。
仿真过程设定船体静止不动,纵、横摇角度均为0°,气流由入口流经船体和上层建筑,从而模拟相对风的测量过程。与风洞试验类似,船体外表面与海平面设定为无滑移壁面,计算域上边界设定为自由滑移壁面。出口边界设定为压力出口。入口边界设定为速度入口,流速剖面采用对数率:

海面10 m高度风速u10N设为5 m/s,卡尔曼常数kv设为0.4,海面粗糙度长度z0设为2 mm。
采用定常方式求解三维不可压缩气流RANS方程,湍流模型选择RNG k-epsilon模型。对流项采用二阶迎风格式,扩散项采用中心差分格式,收敛残差设为10E-4。计算收敛后,输出CFD仿真结果中三个关注区域的平均风速、风向。
1.3 仿真结果分析
自由来流受船体遮挡后产生垂直位移,近海平面气流在船体和上层建筑周围产生钝体绕流,流速、流向均发生改变。图5为特定迎风角度工况下经过测风点处的气流流线图,具体的流速、流向变化情况见表1。

表1 特定迎风角度工况的风速、风向变化

图5 测风传感器安装位置流线图
当0°迎风时,经过3个测风点处气流的垂直位移较小(最大0.6 m),桅杆横桁测风点风速值接近参考测风点风速值,参考测风点风向更接近自由来流。其他3个角度迎风时,气流垂直位移均较为明显(最大垂直位移分别为7.9 m、11 m和10.6 m)。
当90°迎风时,背风侧传感器受遮挡严重,因此风速显著降低,迎风侧传感器风向值更接近自由来流。当45°和135°迎风时,迎风侧传感器风向值更接近自由来流,背风侧传感器风速值高于迎风侧并且变化梯度较大。
左、右舷测风点在不同迎风角度(间隔10°)工况下的风速比例、风向差值如图6所示。随着迎风角度的改变,桅杆左右两侧实际测风点与参考测风点的风速比例变化呈非线性趋势。相对于风速比例,风向差值的变化则更为复杂,无显著规律。

图6 不同迎风角度条件下的风速、风向偏差
从CFD仿真结果可以看出测风偏差与迎风角度直接相关。迎风角度是建立桅杆左右两侧测风点与舰桥上部参考测风点之间风速、风向关系的重要变量。
1.4 测风偏差校正模型
校正测风偏差需建立测风传感器安装高度上未受干扰的自由来流与测风点处受干扰气流之间的映射关系,利用实测数据估计自由来流。通过CFD仿真数据对上述对应关系进行建模是可行的,但是将测风传感器安装到足够远离船体的位置同步采集自由来流数据难以实现,无法利用实验方法直接进行建模和验证。
为解决这一问题,海上实船实验时在舰桥上部特定位置安装一台实验用测风传感器,该安装位置与CFD仿真过程中舰桥上部参考测风点对应,并将其测量值作为参考值。需要指出的是该测风点实际上并不是理想的测风传感器安装位置,同样会受到船体和上层建筑影响。
若利用CFD仿真数据对桅杆左、右横桁与参考测风点处气流之间的非线性关系进行建模,然后通过实船实验数据验证该方法可行,则利用CFD仿真数据对桅杆左、右横桁与CFD仿真入口处的自由来流之间的非线性关系进行建模并估计未受干扰的自由来流,理论上也是可行的。
LSSVM在测量数据非线性关系回归预测方面有着广泛的应用[25]。本文利用LSSVM分别对桅杆左、右横桁测风点和舰桥上部参考测风点处风速、风向之间的非线性关系进行回归,建立测风偏差校正模型。核函数选择高斯核。得到以下关系:

式中:wdm为平均相对风向测量值;rws为风速比例,即桅杆测风点平均相对风速wsm与参考测风点的平均相对风速wsref的比值。Δθ为风向偏差,即桅杆测风点平均相对风向wdm与参考测风点的平均相对风向wdref的差值。
海面平均风测量偏差校正过程如下:(1)根据左、右舷实测风向值得到对应的风速比例和风向差值;(2)按照对应的风速比例分别校正左、右舷实测风速值,按照对应的风向差值分别校正左、右舷实测风向值;(3)对校正后的左、右舷风速、风向值进行矢量平均。
2 实船实验
设计海上实船实验,同步采集不同测风点处的风速、风向数据,对测风偏差校正模型进行验证。海上实船实验与CFD仿真船型一致,各测风点位于桅杆左、右横桁和舰桥上部靠近左舷位置,分别对应于CFD仿真各关注区域的中心。
2.1 实验方法
海面风速、风向采集通过3台测风传感器、1台数据采集器和1台工控机完成。3台测风传感器分别安装于桅杆左、右横桁和舰桥上部,安装点位示意图见图7。桅杆两侧分别安装1台螺旋桨式测风传感器,高度距离海平面26 m,横向距离船体中线面4.06 m;舰桥上部安装1台超声测风传感器,由长度为9 m的支撑杆安装于距海平面23.6 m高度位置,横向距离船体中线面4 m。桅杆两侧与舰桥上部测风点之间的纵向距离为12 m。两种测风传感器测量精度见表2。

图7 测风传感器安装点位示意图

表2 测风传感器测量精度
测风传感器与数据采集器通过RS422串口连接。数据采集器与工控机通过232串口连接,每隔2 s与数据采集器通信并记录当前时刻的瞬时风速、风向值。平均相对风速、风向数据由2 min滑动时间窗口内的瞬时风速、风向数据进行矢量平均后计算得到。
对于桅杆两侧均安装测风传感器的船舶,通常以迎风一侧的测风数据为主(以下称直接输出)。本文对比直接输出和CFD建模校正后的风速、风向偏差,以此检验CFD仿真建模方法校正测风偏差的实际效果。
2.2 数据处理
海上实船实验航次共计48 d,期间经历不同天气、海况条件,记录了包括锚泊和航行状态的瞬时相对风速、风向数据。其中,航行状态下测风数据记录共计30.8万条,风速数据范围为1.1~28 m/s,风向数据范围为0~355°。
从实验数据中选取航行于开阔水域(航速6 kn以上)的风速、风向数据,以便排除锚泊时港口复杂环境(包括大型塔吊和其他大型船舶)对实验船舶周围气流场的干扰。
用矢量平均法处理瞬时相对风速、风向数据,得到平均相对风速、风向数据,然后从处理后的数据中随机选取3 300条平均相对风速、风向数据用于验证CFD仿真建模方法校正测风偏差的实际效果。3个测风点的风速、风向数据分布情况如图8所示。船舶航行时相对风向多以正面来风为主,实测数据集中在相对风向0°附近。船体和上层建筑附体实际上并非左右舷对称,桅杆左、右两侧测风数据的分布存在差异。

图8 测风数据分布情况
3 结果分析
利用实船测风数据验证CFD仿真建模方法校正风速、风向偏差的实际效果,分析影响偏差校正准确性的因素。
3.1 校正效果验证
计算未校正的直接输出方式和CFD建模校正后的风速、风向偏差,结果如图9所示。直接输出风速、风向与参考测风点的数据差异较大,平均风速偏差比例为5.9%(标准差0.05),平均风向偏差为5.8°(标准差4.6)。直接输出的风速比例偏差曲线波动明显,说明不同迎风角度会导致不同程度的风速偏差。CFD仿真建模校正后的风速偏差降低了56%,平均风速偏差比例为2.6%(标准差0.03),但并未完全消除不同迎风角度条件下的风速偏差。CFD仿真建模的平均风向偏差为6.8°(标准差2.7),略大于直接输出的风向偏差,但是对于使用船舶测风数据的应用几乎没有影响。后文将对校正后风速偏差增大的原因做进一步分析。

图9 风速、风向测量偏差校正效果
校正后的风速越接近于参考风速,并且风向偏差越小则证明对测风偏差的校正效果越显著。图10为直接输出和CFD仿真建模校正后的风速比例、风向偏差散点图。经过CFD仿真建模校正后的风速与参考风速比值更接近于1。如果选择传感器安装高度上远离船体(例如CFD仿真入口)的自由来流作为参考,则该方法可用于估计自由来流。

图10 校正后的风速、风向偏差散点图
3.2 误差分析
CFD仿真建模并未完全消除测风偏差,进一步分析在不同迎风角度区间内对左、右舷测风数据校正后的风速、风向偏差分布情况。船舶航行时,相对风向多以正面来风为主,将样本数据按不同迎风角度划分为左舷来风(315°~345°)、右舷来风(15°~45°)和船艏来风(0°±15°)3个区间。

图11 风向数据校正效果对比
对比校正后的左、右舷和模型输出的风向在3个不同区间内的平均偏差(图11),可见模型对左、右舷风向的校正效果并不相同。对左舷测风数据进行校正后,各迎风角度区间的平均风向偏差较大(左舷迎风时为9.9°,船艏迎风时为11.5°,右舷迎风时为4.6°)。实际上,实验船型桅杆两侧附体并非完全对称,而CFD仿真使用简化的船体三维几何模型呈左右舷对称。由于忽略了非对称的局部气流场干扰物,仿真结果中测风点处气流方向与实船存在差异,造成建模校正后的平均风向偏差反而增大。
图12为校正后的左、右舷和模型输出风速的平均偏差对比结果。左舷测风数据校正后的偏差分别为:左舷迎风时5.1%,船艏迎风时1.6%,右舷迎风时2.4%,迎风一侧数据的风速偏差高于背风一侧,表明CFD仿真过程对左侧横桁测风点周围的局部风场干扰物(如球状天线)进行删减会影响建模的准确性。本文采用矢量平均法对校正后的左、右舷风速、风向数据进行合成,即左、右舷数据具有相等的权值,因此左舷建模校正后的较大偏差造成了模型最终输出数据的准确性。
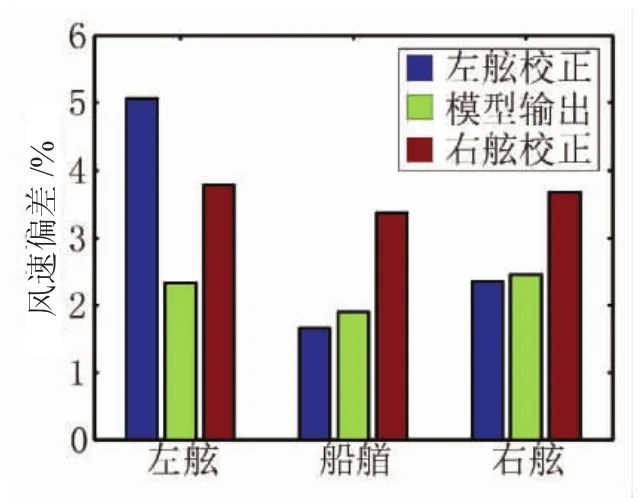
图12 风速数据校正效果对比
4 结论
本文针对船舶海面平均风速、风向测量偏差校正问题,采用CFD仿真方法研究某实验船船体周围钝体绕流气流场的分布情况,利用LSSVM对桅杆左、右横桁与舰桥上部参考测风点风速、风向间的非线性关系进行回归,建立测风偏差校正模型。通过海上实船实验,采集不同测风点的风速、风向数据。验证结果表明CFD仿真建模方法能够有效降低风速偏差56%。该方法便于建立海面自由来流与测风点处受干扰气流之间的非线性关系,可用于估计海面自由来流。CFD仿真过程中对船体三维几何模型的处理应权衡仿真计算量和干扰测风过程的附体结构的删减。本文CFD仿真过程中未考虑船体摇摆,对动态测风数据进行姿态校正后再输入测风偏差校正模型有助于进一步降低测风偏差。
[1]Moat B I,Yelland MJ.Airflowdistortion at anemometer sites on the OWS Polarfront[R].Internal Document No.14,Southampton,UK, National OceanographyCentre Southampton,2009.
[2]Moat BI,Yelland,MJ,Pascal,R W,et al.An overviewofthe airflowdistortion at anemometer sites on ships[J].International Journal of Climatology,2005,25(7):997-1006.
[3]王国峰,赵永生,范云生.风速风向测量误差补偿算法的研究[J].仪器仪表学报,2013,34(4):786-790.
[4]周亦武,王国锋,赵永生.船舶摇摆状态下风速测量误差分析与补偿研究[J].仪器仪表学报,2014,35(6):1239-1245.
[5]EdsonJB,HintonAA,PradaKE,etal.Directcovariancefluxestimatesfrommobileplatformsatsea[J].JournalofAtmospheric&Oceanic Technology,1998,15(2):547-562.
[6]Landwehr S,O'sullivan N,Ward B.Direct flux measurements from mobile platforms at sea:motion and air-flow distortion corrections revisited[J].Journal ofAtmospheric&Oceanic Technology,2015,32(6):1163-1178.
[7]Dobson F W.Review of reference height for and averaging time of surface wind measurements at sea (Marine Meteorology and Related Oceanographic Activities Report No.3)[R].World Meteorological Organization,Geneva,Switzerland,1981.
[8]World Meteorological Organization.Guide toMeteorological Instruments and Methods ofObservation[M].WMO-No.8.Seventh Edition, World Meteorological Organization,Geneva,Switzerland,2008.
[9]Yelland MJ,Moat B I,Pascal R W,et al.CFD model estimates ofthe airflowdistortion over research ships and the impact on momentumfluxmeasurements[J].Journal ofAtmospheric&Oceanic Technology,2002,19(10):1477-1499.
[10]行鸿彦,于祥,邹水平,等.风杯式风速传感器启动风速校准实验箱的分析与设计[J].仪器仪表学报,2015,36(9):1996-2004.
[11]Dupius H,Guerin C,Hauser D,et al.Impact of flow distortion corrections on turbulent fluxes estimated by the inertial dissipation method duringthe FETCH experiment on R/VL’Atalante[J].Journal ofGeophysical Research,2003,108(C3):8064.
[12]Popinet S,Smith M,Stevens C.Experimental and numerical study ofthe turbulence characteristics ofairflowaround a research vessel [J].J Atmos Ocean Tech,2004,21(10):1575-1589.
[13]Moat B I,Yelland MJ,Pascal R W,et al.Quantifying the airflowdistortion over merchant ships.part I:validation of a cfd model[J]. Journal ofAtmospheric&Oceanic Technology,2006,23(3):341-350.
[14]Moat B I,Yelland MJ,Molland A F.Quantifying the airflowdistortion over merchant ships.partⅡ:application of the model results [J].Journal ofAtmospheric&Oceanic Technology,2006,23(3):351-360.
[15]Griessbaum F,Moat B I,Narita Y,et al.Uncertainties in wind speed dependent CO2transfer velocities due to airflow distortion at anemometer sites on ships[J].J Atmos ChemPhys,2009,9(11):5123-5133.
[16]O’Sullivan N,Landwehr S,Ward B.Air-flow distortion and wave interactions on research vessels:an experimental and numerical comparison[J].Methods in Oceanography,2015,12:1-17.
[17]PolskySA.Acomputationalstudyofunsteadyshipairwake[C]//40thAIAAAerospaceSciencesMeeting&Exhibit,Reno,Nevada,2002: 2002-1022.
[18]Wnęk A,Guedes Soares C.Cfd assessment of the wind loads on an lng carrier and floating platform models[J].Ocean Engineering, 2015,97:30-36.
[19]贺少华,刘东岳,谭大力,等.载机舰船气流场相关研究综述[J].舰船科学技术,2014,36(2):1-7.
[20]王伟.大型舰船流场的数值计算[D].哈尔滨:哈尔滨工程大学,2011.
[21]赵永振.大型舰船定常与非定常气流场数值模拟[D].哈尔滨:哈尔滨工程大学,2012.
[22]郜冶,刘长猛.护卫舰气流场数值计算研究[J].哈尔滨工程大学学报,2013,34(5):599-603.
[23]洪伟宏,姜治芳,王涛.上层建筑形式及布局对舰船空气流场的影响[J].中国舰船研究,2009,4(2):53-58,68.
[24]陆超,姜治芳,王涛.不同工况条件对舰船舰面空气流场的影响[J].舰船科学技术,2009(9):38-42.
[25]郭颜萍,胡桐,漆随平.基于小波变换和LS-SVM的船面风速风向估算方法[J].海洋技术学报,2016,35(2):66-70.
A Bias Correction Method of Ship Wind Measurement Based on Airflow Field Simulation
HU Tong,QI Sui-ping,GUO Yan-ping,WANG Dong-ming
Shandong Provincial Key Laboratory of Ocean Environmental Monitoring Technology,Institute of Oceanographic Instrumentation, Shandong Academy of Sciences,National Engineering and Technological Research Center of Marine Monitoring Equipment,Qingdao 266001,Shandong Province,China
Shipboard sea surface wind measurement is affected by the airflow distortion caused by ship hull and superstructure,which leads to measurement data bias.To address the bias correction problem for the relative wind measurement bias from shipborne anemometer,this paper adopts the CFD simulation method to study the airflow field around the ship hull and superstructure in order to quantitively analyze the wind-bias between the anemometers installed on both sides of the mast and the anemometer installed above the bridge for reference purposes.Then LSSVM is applied to establish the wind-bias correction model.To validate the correction effect of the proposed method,an experimental voyage was undertaken to collect wind measurements from corresponding measurement points.The results show that the CFD-based wind-bias correction model can effectively reduce 56%of the wind speed bias.
ship airflow field;CFD;wind measurement;bias correction
TH765
A
1003-2029(2017)02-0028-07
10.3969/j.issn.1003-2029.2017.02.005
2017-07-04
国家自然科学基金资助项目(41606112);山东省科学院青年基金资助项目(2014QN034);山东省重点研发计划资助项目(2015GSF115018)
胡桐(1983-),博士,助理研究员,现从事船舶气象观测相关问题研究。Email:tong.hu@hotmail.com
