基于傅里叶变换和kNNI的周期性时序数据缺失值补全算法

贾梓健+宋腾炜+王建新

摘 要：在机器学习和数据挖掘过程中，数据缺失现象经常发生。对缺失值的有效补全是数据预处理的重要组成部分，也是后续分析挖掘工作的基础。最近邻填充算法（kNNI）因其易于实现、计算方便和局部填充效果好等特性而被广泛应用。但是，它并不涉及全局信息，因而当大段缺失值发生时，补全效果会有所降低，而对于具有周期成分的时序数据，其效果更是急剧下降。幸运的是，傅里叶变换能够解析出周期数据中的不同周期成分，并能在此基础上通过逆变换基本实现数据复原，只不过其局部复原能力较弱。因此，本文结合傅里叶变换对周期性数据的全局复原能力和kNNI对局部数据的补全能力，提出了基于傅里叶变换的kNNI缺失值补全算法（FkNNI）。通过对大量模拟数据的测试结果表明，该算法比单纯的kNNI算法的缺失值补全准确性有很大提升。

关键词：缺失值补全；最近邻填充算法；周期数据；傅里叶变换

中图分类号：TP391.4 文献标识码：A

Abstract：Data missing often occurs during the process of machine learning and data mining.Missing value imputation is an important part of data preprocessing and is also a basis for subsequent work of analysis and mining.The algorithm of k-Nearest Neighbor Imputation （kNNI） is a popular method frequently employed for missing value imputation because it is easy to implement，easy to calculate and effective for local data completion. However，it does not involve global information， and as a result，its effect decreases somewhat when large fragments of missing values occur，especially when there are periodic components in the time series data.Fourier transform， however，is able to analyze the different periodic components in the periodic data，and to roughly restore the data by inverse transform， with its local recovery ability weak only.Therefore，this paper proposes akNNI algorithm based on Fourier transform （FkNNI），combining the global recovery ability of Fourier transform and the local recovery ability of kNNI.Experimental testing results on a large amount of data indicate that the new algorithm is far more accurate than kNNI only.

Keywords：missing value imputation；kNNI；cyclical data；Fourier transform

1 引言（Introduction）

人類自2010年便进入到大数据时代，大数据时代的来临，给数据挖掘技术带来了许多机遇与挑战。如今，我们对大数据的研究不再采用抽样调查的方法，而是对所有数据进行全面分析。大数据显著的特点是种类多、流速快及数据量大，因此需要我们灵活运用数据挖掘技术对各种数据进行聚类、分类、分析，以及对其趋势进行预测。

在数据挖掘和机器学习中，经常会出现数据缺失的现象[1]。造成数据损失的原因有很多，如信息意外遗漏、无法获取、系统实时性要求太高或收集代价太大等，都可能导致数据缺失。数据缺失会影响数据挖掘过程中抽取规则的准确性，甚至会导致建立错误的数据挖掘模型，目前常用的数据缺失值处理方法有如下三类：

第一类方法直接删除元組。这种方法简单易行，若包含缺失值的元组在整体数据中所占比较小，则该方法非常有效。然而，当缺失值所占比例波动很大时，该方法会降低数据挖掘算法的质量。同时，忽略的元组可能包含重要信息，使数据发生偏离，甚至得出错误的结论。

第二类方法对数据进行推测和补齐。该方法一般基于统计学原理，用不同的算法对缺失值进行填充，常见的数据补齐算法有：平均值（或中位数）填充、特殊值填充、热卡填充、人工填充、k-最近邻法、回归和EM算法等。

第三类方法不做任何处理，但并不影响挖掘方法正常运行。该方法指直接在包含缺失值的数据集上进行数据挖掘，常见的方法有贝叶斯网络和人工神经网络等[1]。

很多研究表明，采用合适的算法针对特定的数据类型的数据集，能够产生较好的填充效果。

本文的研究对象是时序数据缺失值的填充方法。与一般数据不同，时序数据一般来说具有明显的趋势性和周期性，其全局特点非常明显。也就是说，某个时间点的数据不但与其邻近数据有明显的关系，它与全局数据都有关联。因此，我们不但要采纳局部数据补全的优秀补全算法，也要考虑具有全局数据处理能力的补全算法，并希望把它们有机结合。基于这样的思想，本文在kNNI[2]算法的基础上提出了基于周期频谱分析的缺失值补全算法，并在模拟数据和真实数据上进行了验证。

本文的整体结构如下：第2部分介绍了相关的工作，包括线性拟合算法、傅里叶变换和kNNI算法算法等，第3部分介绍了FkNNI算法的基本框架，第4部分是实验结果和结论。

2 相关工作（Related work）

缺失值补全算法的核心目标是提取数据间的相关关系，并以此为基础建立模型，按照模型填充和补全缺失的数据。但时序周期数据之间的关系非常复杂，涉及数据的线性趋势，也就是数据随时间变化而在总体趋势上的线性增长或减少的趋势。另外一个关系是数据随时间呈现的周期规律，并且这种周期在大多数情况下并不是单一周期，而是若干个周期的合成。因此，需要用傅里叶变换等工具发现其周期成分，也就是频谱分析。数据间的第三个关系是局部数据的相似性，也就是相邻数据间的值的差别不会很大。因此，以下将从线性趋势、周期规律和局部关系三个方面，介绍缺失值补全的已有的基础和成果。

2.1 线性拟合

如果离散函数值{f1，f2，…，fn}中有k个值缺失，则可以利用非缺失的n-k个值进行线性拟合，得到式（1）所示的公式。然后，对缺失的k个值，逐一代入式（1）中，所获得的线性函数值就是需要补全的值。

线性拟合所得的公式（1）不但可以用于补全缺失数据，也可以在整体数据上进行消除其增加或减少的趋势。例如，如果离散函数值{f1，f2，…，fn}线性拟合所得到的线性拟合公式为式（1），那么把所有的离散值减去该公式对应的函数值就可以得到另外一组函数值{g1，g2，…，gn}，这组函数值具有良好的性质：其均值是0，其线性拟合公式中参数a和b的值都是0，因而比原数据更适合采用傅里叶变换等的操作。因此，线性拟合操作及基于此的平移旋转工作往往是其它操作的基础。

2.2 傅里叶变换分析

傅里叶变换（Fourier Transform）是一种线性积分变换[4]，通过它可以把信号从时间域变换到频率域，进而研究信号的频谱结构和变化规律。它在物理学、信号处理、统计学、声学、光学等领域都有着广泛的应用。

很多时序数据虽然看似杂乱无章，并不能观察到其周期，其实很可能是由多个周期控制的规律性极强的数据。傅里叶定理表明，对于任何连续记录的时间序列或信号，都可用无限叠加的不同频率的正交的正弦波信号表示。因此可将时间序列进行傅里叶变换，计算序列的周期特征并进行频谱分析，进而通过逆变换，对序列做进一步的分析处理。

在傅里叶逆变换过程中需要两个条件，一个是每个正弦波的振幅，另一个是每个正弦波的相位差。因此通过傅里叶变换，我们把看似杂乱无章的信号考虑成由一定振幅、相位、频率的基本正弦信号组合而成，傅里叶变换的目的就是找出这些基本正弦信号中振幅较大的频率，从而找出主要的频率。

根据原信号的不同类型，我们可以把傅立叶变换分为四种类别[5，6]：

（1）非周期性连续信号：傅立叶变换。

（2）周期性连续信号：傅立叶级数。

（3）非周期性离散信号：离散时域傅立叶变换。

（4）周期性离散信号：离散傅立叶变换。

四种原信号的图例如图1所示。

对于时间序列而言，该函数的值越越大，则说明函数与原始数据集越贴近，因此选用结果较大的正弦函数用来进行叠加处理。

如果通过傅里叶变换的结果如图2所示，那么对周期性离散信号，原始数据值f（i）（图中用虚线表示）和我们进行拟合的函数在该点的值sin（i）（图中用实线表示）的贴合程度决定了拟合度的好坏。

式（5）中的k的选择要根据傅里叶变换的实际情况，就是取周期性非常显著的几个频率，最小取1，最大一般可以取到7，通常是取2至4，图2中的逼近函数的k取1。

2.3 kNNI算法

k近邻算法（kNN）是一种理论比较成熟的、且最简单的分类算法之一。它操作简单，时间复杂度低，用于缺失值补全时，其插补精度高，因此被广泛运用于机器学习的众多领域。它可以作为分类算法，其思路为：如果一个样本在特征空间中的k个最相似的样本中的大多数属于某一个类别，则该样本也属于这个类别。该算法基本流程如图3所示。

kNN算法还可以用于回归，其原理是在样本附近取k个样本，将这些样本某属性的平均值赋给该样本，将不同距离的邻居对该样本产生的影响赋予不同的权值。就可以得到该样本的属性。

k近邻填充算法（k-Nearest Neighbor Imputation Method， kNNI）是kNN算法在缺失值補全领域的应用[8]。通过kNNI来进行缺失值填充的核心思想是计算缺失数据项到各个完全数据集的距离，选取距离该缺失数据项的k个最近邻数据作为基础和依据，把它们加权，用来进行缺失值填充。

kNNI算法在缺失值补全时依然有一些不足之处，例如，（1）当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的k个邻居中大容量类的样本占多数。（2）计算量较大，每一个待分类的样本都要计算它到全体已知样本的距离，才能求得它的k最近邻点。（3）由kNNI算法选择的最近邻居可能导致具有不同方向的偏好，使得分类结果失效。针对这些问题，目前许多可行的解决方法，如采用与距离相关的权值的方法或事先对已知样本点进行剪辑，去除对分类作用不大的样本等[9]。

如图4所示，若原始数据点集在处数据值缺失，那么kNNI算法即为，选取落在其左右一段等距的区间内的原始数据点，将这些点的值取均值，即认为该值就是处数据的缺失值。

如前文所述，kNNI算法由于很多优秀的性质而被广泛采用。然而，kNNI算法的填充准确性很大程度上依赖于k值的选择。而通常k的值要通过遍历才能最终确定，这需要大量的计算投入[10]。

3 算法框架（Algorithm framework）

缺失值补全算法的实质是通过数据间内在的关系，发现其中的模型和规律，从而从未缺失的数据和规律出发，推测出缺失的数据。我们需要处理的数据是生态监测领域的通量塔检测数据，包含了水中的氧气含量、二氧化碳含量、碳通量等的时序数据，这些数据呈现出明显的趋势性和周期性，而且周期性多以天和年为主要周期成分。因此，对于其中的缺失值补全，需要同时考虑趋势性和周期性，同时也要考虑近邻数据与缺失数据之间的相似关系。

对一个时序数据序列，FkNNI填充算法主要经过如下几个主要步骤：

步骤1，通过线性拟合，计算出如式（1）所示的拟合公式。

步骤2，在原始数据的基础上，减去式（1）计算所得的模型值。此时，所有时序数据的平均值是0，且其线性拟合直线就是x轴本身。

步骤3，通过式（4）所示的离散傅里叶变换，得到不同周期的正弦函数对应的系数（振幅），并找到最主要的几个周期，也就是发现其主要的频谱。

步骤4，按照式（5）把缺失值所在的时间点的数据补全为傅里叶逆变换的函数值。

步骤5，利用式（1）把补全的数据复原为带线性趋势的数据，这部分是傅里叶变换所得的补全值。

步骤6，用kNNI算法，对邻近非缺失的值进行加权平均，也得到一个补全数据，这是kNNI所得的补全值。

步骤7，把第5步和第6步所得数据进行线性加权，如果是大段缺失，则对第5步所得的补全值占有更大的比重；如果是单点缺失，则要提高kNNI所得补全值的比重。线性组合方式如式（6）所示。

其中，在0和1之间，是合成的补全值，和分别是傅里叶变换补全值和kNNI补全值。

由于新提出的算法框架是基于数据的全局关系（傅里叶变换和线性趋势所描述的关系）和局部关系（kNNI所描述的关系）两个方面，因此称之为FkNNI。

4 实验结果与结论（Experimental results and conclusions）

我们采用的原始数据是通量塔的时序数据及相关模拟数据，在数据中人为去除一些数据，形成缺失值，然然后逐步采用第3部分给出的算法框架，得相应的补全值。把原始去除的数据与补全数据相比较，便可得到对对补全算法的精确性的度量。

实验和结果

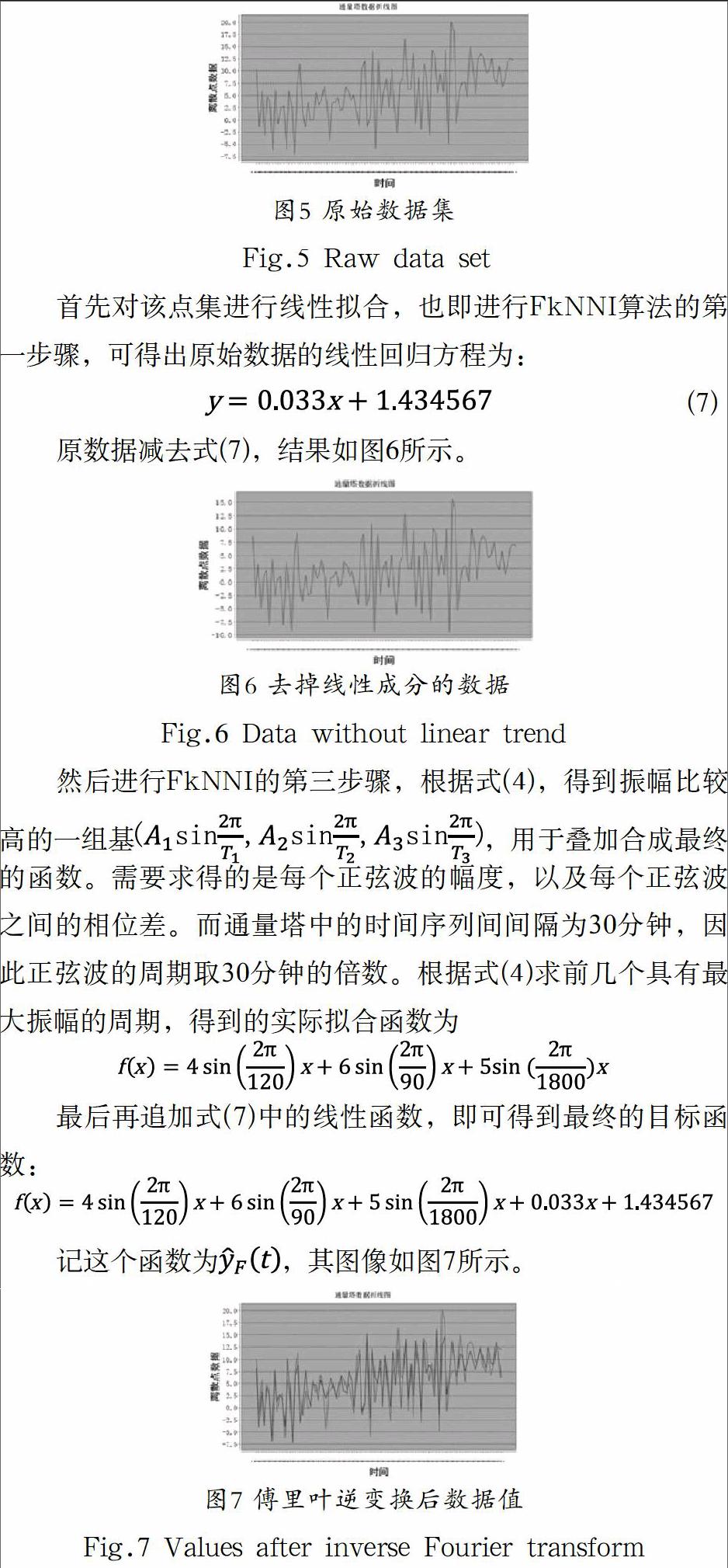
通量塔获取的原始的时序数据如图5所示，其中横轴表示时间，纵轴是时序数据的观测值。为了测试缺失值填补的精确性，我们事先去除掉一部分数据作为缺失值。

然后进行FkNNI的第三步骤，根据式（4），得到振幅比较高的一组基，用于叠加合成最终的函数。需要求得的是每个正弦波的幅度，以及每个正弦波之间的相位差。而通量塔中的时间序列间间隔为30分钟，因此正弦波的周期取30分钟的倍数。根据式（4）求前几个具有最大振幅的周期，得到的实际拟合函数为

若在时间序列上，时刻的数据值发生了缺失，上文中基于离散傅里叶变换求得的函数在该时刻的函数值设为，利用kNNI算法，取左右各100分钟的时间间隔，将落在该区间内的原始数据值取均值得到结果为，根据式（6），利用FkNNI算法计算时刻缺失的数据值为两个补全值的线性组合。

式（6）中的，若经傅里叶变换后得到的函数周期性较好，则取较大值，反之取较小值。

为了验证补全效果，我们随机去除5个时间点的数据，人为造成数据缺失。这5个时间点如表1的第1列所示，缺失前的真实值在表格的第2列。通过kNNI算法和FkNNI算法得到的模型值和分别在表格的第3列和第4列。

从表1可以看出，用新算法FkNNI得到的模型值比kNNI要更接近原始值。事实上，kNNI补全值的平均误差为1.2363，而FkNNI补全值的平均误差只有0.3562，具有一定的优势。

通过表1中的对比，我们可以看出kNNI算法和FkNNI算法在对单点的缺失进行补全的时候，都有一定的准确性。但是影响通量塔中的数据的因素很多，难免会出现整段缺失的现象，此时，如果对这一段中所有缺失的点都采用kNNI算法进行补全的话，这一段上的补全的值大致相同，这与实际数据就会相差甚远。所以此时我们将采用FkNNI算法，来较好的复原一段丢失的数据。

由于我们采用等间隔采样的数据，因此，对于大段缺失的数据，我们利用缺失点为中心的区间内的非缺失点作为补全的基础。也就是说，计算某个缺失值时所采用的两边的非缺失点的数量很有可能不一样多。

表2中的数据去除了第71至75个时刻之间的所有值作為缺失值。表2的第2、3、4列分别是原始值，kNNI补全的模型值和FkNNI补全的模型值。

从表2可以看出，FkNNI的模型值比kNNI的模型值与原始值之间要相似得多。事实上，kNNI的模型值的平均误差是5.0212，而FkNNI的模型值的平均误差是1.0430，平均误差非常显著地降低。

从表1和表2中的模型比较可以看出，FkNNI算法在缺失值补全的精度上要优于kNNI算法，并且对大段缺失这种优势更加明显。对于含有峰值的大段缺失，kNNI算法不能复原任何峰值，但FkNNI具备复原峰值或逼近峰值等能力。

5 结论（Conclusions）

采用数据挖掘算法对数据进行挖掘并从中发现知识的前提是具有较高质量的数据。然而，由于种种因素，在实际应用中采集的数据通常都会出现缺失。缺失值补全具有重要的理论和实践意义。通过对时序数据的观察和分析，我们认为时序数据间的关系主要由三个方面构成：邻近数据的相似性、数据的线性趋势和数据的周期规律。基于此，本文提出了基于傅里叶变换的和kNNI的缺失值补全算法FkNNI，准确把握了数据间的内在关系规律，使得数据补全的准确性有了较大提升；尤其是在大段数值缺失时，该算法的补全优势就更为明显。这为综合利用数据的全局和局部关系信息提供了新的思路。

参考文献（References）

[1] Tutunji，Tarek A.Parametric System Identification Using Neural Networks[J].Applied Soft Computing Journal，2016，47（1）： 251-261.

[2] Jianxin WANG，et al.Imputating Missing Values with Distance-and Density-Weighted and Quadrant-Based Nearest Neighbors[J].Journal of Computational Information Systems，2015，11（18）：6605-6612.

[3] Tao Zhou，Akil Narayan，ZhiqiangXu.Multivariate Discrete Least-Squares Approximations with a New Type of Collocation Grid[J].SIAM Journal on Scientific Computing，2014，36（5）： A2410-A2422.

[4] 黄雄波.多周期时序数据的傅氏级数拟合算法的计算机系统应化，2015，24（7）：142-148.

[5] 陳岗.离散数列的傅立叶变换[J].科技资讯，2016，27（9）：141-142.

[6] 司新新，李佳.傅立叶变换在数字信号处理中的分类研究[J].中国新通讯，2016，14：122-123.

[7] J Yang，Y Zhang，W Yin.A Fast Alternating Direction Methodfor TVL1-L2 Signal Reconstruction From Partial Fourier Data[J]. 2010，4（2）：288-297.

[8] Caren Kasler，Yves Tille，Balanced.k-Nearst neighbour imputation[J].Statistics，2016，50（6）：1310-1331.

[9] Luengo J，Saez J A，Herrera F.Missing Data Imputation for Fuzzy Rule-Based Classification Systems[J].Soft Computing，2012，16（5）：863-881.

[10] C.Yozgatligil，et al.Batmaz.Comparison of Missing Value Imputation Methods in Time Series：the Case of Turkish Meteorological Data[J].The Oretical and Applied Climatology， 2013，112：1-2.

作者简介：

贾梓健（1996-），男，本科生.研究领域：软件工程.

宋腾炜（1996-），女，本科生.研究领域：软件工程.

王建新（1972-），男，博士，教授.研究领域：软件测试，软件工程，数据挖掘.本文通讯作者.