基于余热发电的微电网储能优化配置研究

魏振洋

（国网陕西省电力公司，陕西 西安 710075）

0 引 言

目前，随着余热发电技术的日益成熟及广泛应用，建材企业的传统水泥生产模式在加入余热发电项目后，不仅对降低能耗、减少电费支出等方面具有积极的意义，同时对整个供电系统的可靠性、先进性也有很大的技术支撑。但同时应看到，随着余热发电项目的实施，整个系统的控制变得更为复杂：整个生产过程中的水、气、尘等过程更加构成一个有机循环的整体。以供电系统为例，没有余热发电项目之前属于纯粹的受电系统，而在余热发电加入后则变为典型的具有发、输、配特征的微电网系统，特别是一个厂区内具有多条水泥生产线、余热发电和生产线形成点对点关系更具有典型性；随着售电市场的放开及直供市场的进一步优化，相信越来越多的建材企业将加入到构建自己的供电网络大军中来，因为这样不仅可以自发自用节约成本，而且可以发挥更大的专业优势，开展跨行业多种经营；对电力系统而言，最重要的就是各种故障的研判；对微电网而言就是基于故障研判基础上的储能设备优化配置。

国内外研究机构针对微电网中的储能设备的优化配置问题进行了相关研究，将储能系统应用到微电网中，其容量问题是不得不考虑的，因为容量小了不能为微电网提供经济性，所需的灵活性以及可靠性要求，容量太大了将会增加系统的投资成本和维护费用[1]。因此必须对储能设备的容量进行优化，以达到减少微电网的运行成本和投资。文献[2]考虑电力系统可靠性要求，提出了一个确定系统备用储能容量大小的分析方法，备用能源可以以电能或燃料形式存储。文献[3]研究了面对时段收费工业客户的储能容量问题。

1 支路势能暂态能量函数

1.1 基于实际故障轨迹的支路暂态能量函数

在一多机电力系统中，在原来结构保留模型的电网中，加入代表虚拟的发电机的内电势节点，形成一个结构保持的增广系统，其能量函数为：

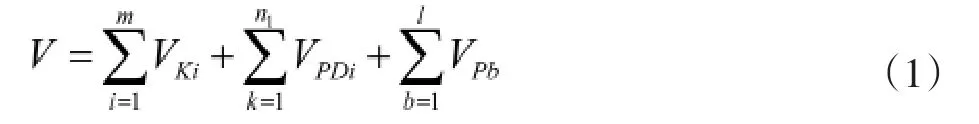
沿网络实际轨迹构造能量函数时，整个网络的动能就是每台发电机的动能之和，整个网络的势能则可以表示为增广系统中所有支路的暂态势能和负荷的暂态势能的之和。

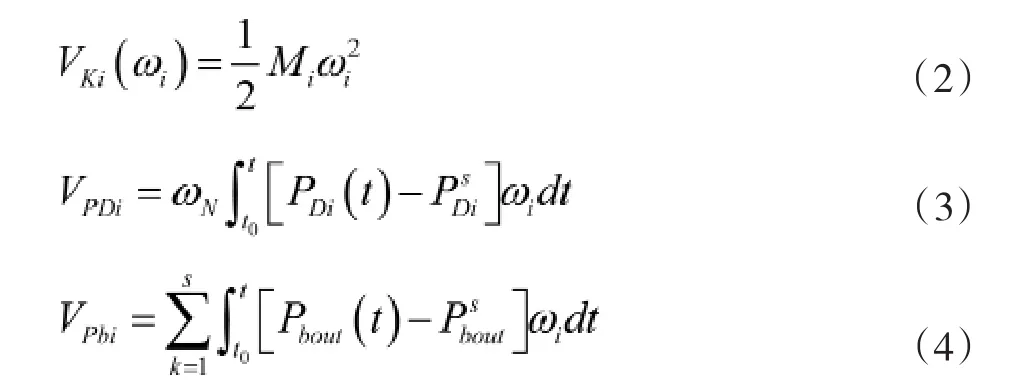
1.2 微电网支路暂态能量函数

微电网结构保留模型能量函数的外势能Vp可表示成如下形式：

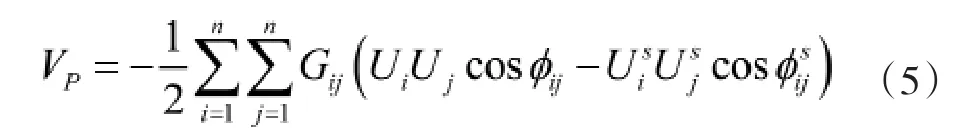
根据上一节中系统支路暂态能量函数的构造方法，上式微电网系统的外势能Vp可用每条支路能量来表示，即微电网支路暂态能量函数V′p，i-j表示如下：

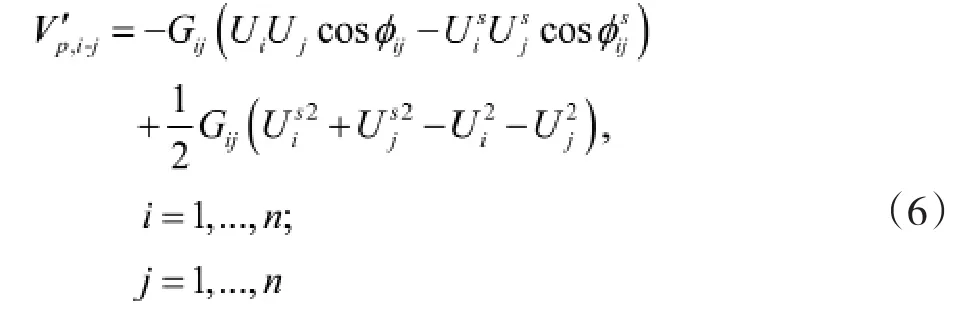
2 基于微电网支路暂态能量函数的储能优化方法

基于微电网支路暂态能量函数的储能优化布局基本步骤如下。

2.1 微电网系统故障扫描

不管微电网系统是否稳定，其系统的外势能总是会有一个最小的极值点Vpmin。系统Vpmin随故障切除时间tcr的变化趋势见图1。

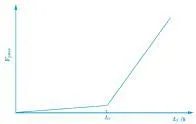
图1 Vpmin随tcr变化曲线

（1）系统故障后，其Vpmin曲线由接近线性的两个部分构成，分别是系统的稳定和不稳定情况下的轨迹；

（2）不稳定情况下对应的轨迹相对比较陡，稳定轨迹情况下对应的轨迹相对比较平，并且数值也较小；

（3）系统故障后的Vpmin曲线有一拐点对应的是故障临界切除时间tcr。

2.2 微电网系统暂态能量分布特性

通过观察各支路暂态能量的分布情况，来分析系统的暂态稳定性。当一个微电网系统失稳时，它的某一条支路两端的支路角就会变得很大，对应支路的暂态势能就会在整个势能中占的比重就会很大，系统也会在该支路上因失去稳定而发生解列。所以，把该支路当作系统的脆弱支路，相应的最大势能支路就是系统的最脆弱支路。该最脆弱支路就被视为储能设备的最优安装位置。

3 仿真分析

为了验证本章所提出的微电网系统储能优化配置方法的有效性，本章在MATLAB/SIMULINK仿真环境中对所建立的模型进行了系统仿真实验，一个3机9母线仿真系统见图2。系统中每个逆变电源的额定功率为10kW，下垂系数为mi=le-5，ni=3e-4，i=1，2，3。

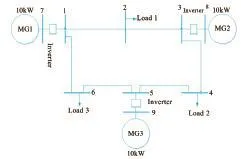
图2 系统仿真结构图

3.1 系统故障扫描

对该仿真系统的不同位置设置三相短路故障（3LG）、两相接地短路故障（2LG）、两相短路故障（2LS）和单相短路（1LG）故障，通过不断改变故障切除时间tcl，求取在不同的类型故障状态下系统的故障临界切除时间tcr。

从表1可以看出，当在同一地点发生故障时，系统发生3LG故障时，tcr的值最小，发生1LG故障时，tcr的值最大。所以3LG故障是该系统最严重的故障类型。同时，当3LG故障发生在支路3-4时，tcr的值最小，也就是说，此时系统的暂态稳定性是最差的，即该故障状态为系统的最严重故障。

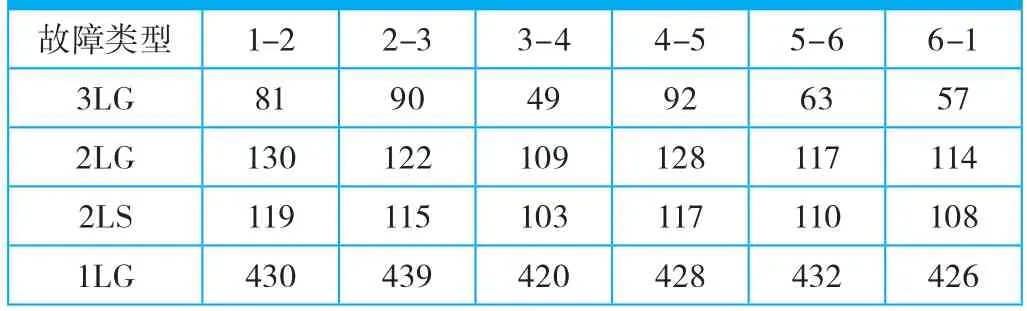
表1 不同位置发生不同类型故障时系统tcr的值（ms）

3.2 系统暂态能量分布特性

从表1可知，对所有故障类型来说，故障发生在支路3-4是最严重的故障状态。为了确定系统最脆弱支路，对于3LG、2LG和2LS故障，故障发生时刻为0.65s，故障切除时刻为0.77s，对于1LG故障，故障发生时刻为0.65s，故障切除时刻为1.08s。

如图3所示，系统此时没有达到稳定运行状态。支路2-3上的暂态势能值最大，也就是说在暂态过程中，该支路受到的暂态能量的冲击是最严重的，系支路2-3就是该系统在此种失稳情况下的最薄弱支路。而支路3-4为次薄弱支路，并且对3LG，2LG，2LS故障来说，各支路暂态势能比重分布情况是一样的。所以将母线3作为储能的最佳安装位置。

表2描述了故障发生在支路3-4时的V′crp，2-3值大小，V′crp，2-3的值可以用来判断系统的稳定程度以及储能设备安装在不同位置时对系统的稳定效果。

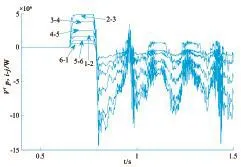
图3 系统各支路暂态势能分布图

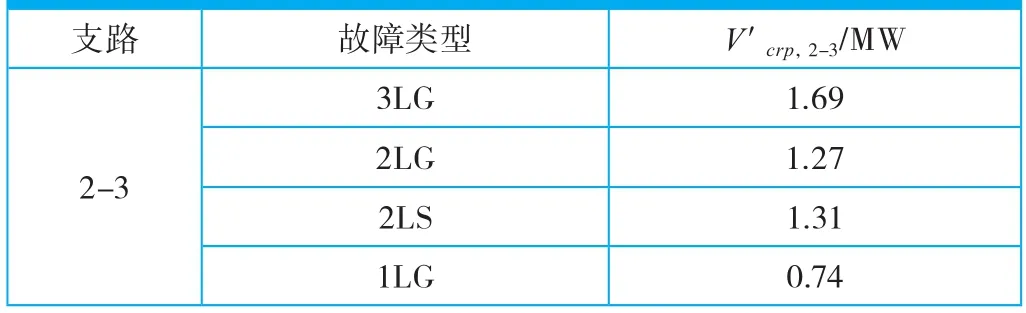
表2 支路3-4发生不同类型故障时V′crp，2-3

3.3 储能设备优化布局

从表3可以看出，储能设备安装在母线3上时，对所有故障类型，其对系统暂态稳定性效果是最好的，支路2-3暂态势能Vp，2-3和系统内势能波动最小，而且数值趋向于0，说明在此种布局方案下，储能设备对系统暂态能量的抑制作用最好，能够有效地抑制故障向系统注入不稳定能量。而且从表3可以得到，对所有故障类型，当储能设备安装在母线3上时，V′maxp，i-j和IPE的值是最小的。所以储能设备的最佳安装位置是母线3。

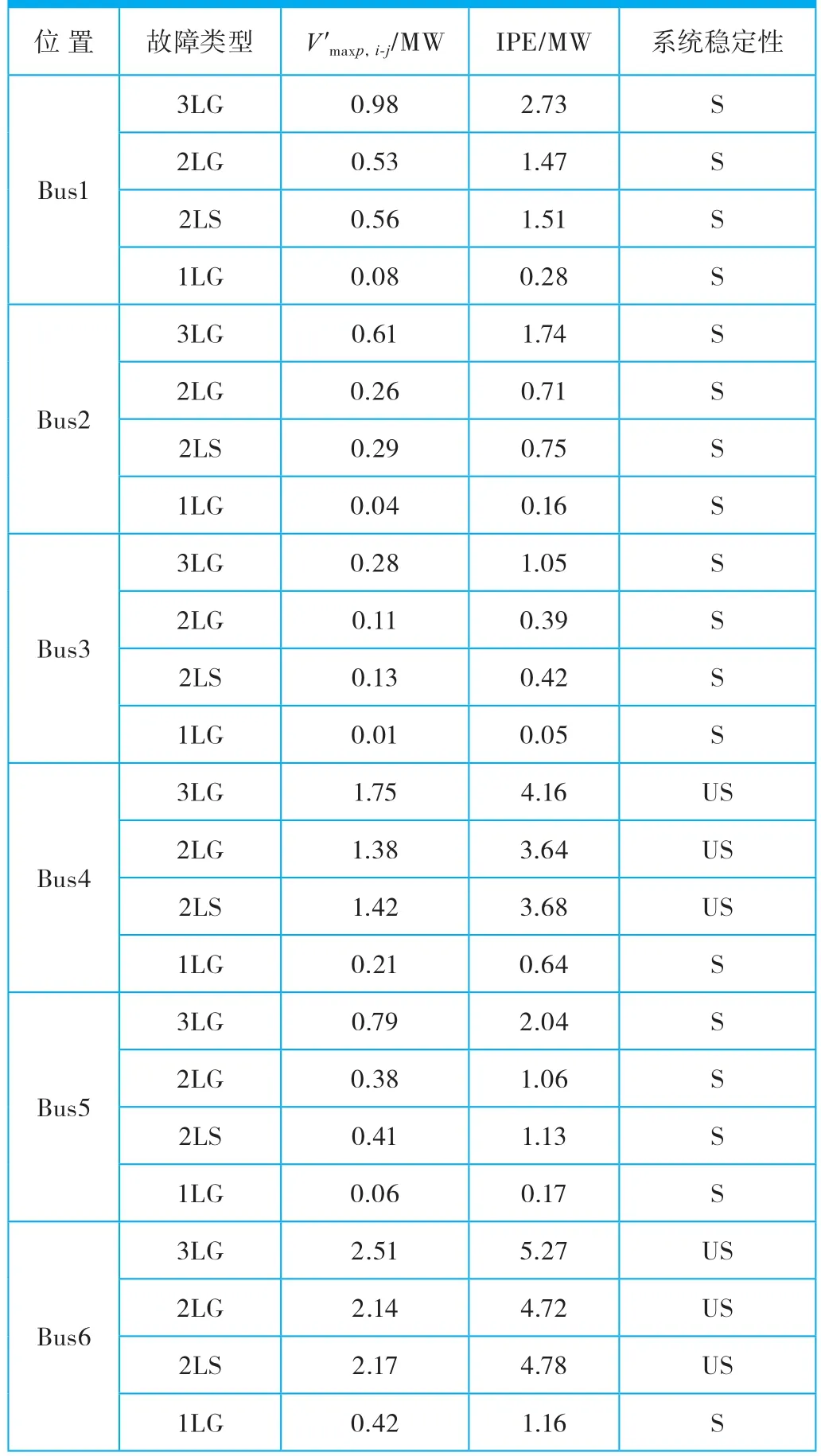
表3 储能设备安装在不同母线上，支路3-4发生不同类型故障时V′maxp，i-j和IPE的值

4 结 论

本文首先学习了支路暂态能量函数的相关内容，构造了适合微电网环境的微电网支路暂态能量函数，基于该支路能量函数，将微电网暂态能量函数的外势能等效到每一条支路上，即用支路能量表示系统外势能。通过找寻支路势能最大值的支路，来确定系统最薄弱支路，最后确定储能设备的最佳安装位置。设计了多微电网互联系统的储能优化配置方法。最后通过仿真实验和结果分析，证明了所提方法是有效和可行的。

参考文献：

[1]Bahramirad S，Reder W，Khodaei A. Reliability-constrained optimal sizing of energy storage system in a microgrid[J]. Smart Grid，IEEE Transactions on，2012，3（4）：2056-2062.

[2]Mitra J. Reliability-based sizing of backup storage[J]. IEEE Transactions on Power Systems，2010，25（2）：1198-1199.

[3]Lee T Y，Chen N. Determination of optimal contract capacities and optimal sizes of battery energy storage systems for timeof-use rates industrial customers[J]. Energy Conversion，IEEE Transactions on，1995，10（3）：562-568.