基于MEMS传感器的四旋翼组合测姿研究

戴邵武,李松林,邢志川,丁广威,袁 鹏,康宇航

(1.海军航空工程学院,山东 烟台 264001；2.91467部队,山东 青岛 266311；3.91206部队, 山东 青岛 266108;4.92330部队,山东 青岛 266001)

基于MEMS传感器的四旋翼组合测姿研究

戴邵武1,李松林1,邢志川2,丁广威3,袁 鹏4,康宇航1

(1.海军航空工程学院,山东 烟台 264001；2.91467部队,山东 青岛 266311；3.91206部队, 山东 青岛 266108;4.92330部队,山东 青岛 266001)

针对四旋翼无人机机体尺寸较小、带载荷能力有限的特点,设计基于低成本MEMS惯性器件的测姿系统,以满足四旋翼无人机在系统控制方面的需求。但是低成本的MEMS惯性器件具有精度低,随机漂移大,容易受到外界环境干扰等缺点。本文充分发挥四旋翼无人机搭载的MEMS惯性器件的功能,分别利用两种方法测量载体姿态,并通过卡尔曼滤波的方法实现这两种测姿方法的数据融合。经过仿真分析,融合后组合测姿系统的测姿精度得到提高。

测姿系统;MEMS惯性器件;Kalman滤波;数据融合

0 引言

最近几年在全世界范围内,无人机的应用迅速蔓延开来。民用领域,无人机主要用于航拍、环境监测、新闻报道、天气预报、喷洒农药等；军用领域,无人机则用于靶机、电子侦察、骗敌诱饵、实施干扰等任务[1]。无人机按结构分为固定翼无人机和旋翼无人机。四旋翼无人机是旋翼无人机的典型代表。四旋翼无人机与固定翼无人机的不同之处在于四旋翼无人机的升力由旋翼旋转产生,而固定翼无人机的升力则来自机翼,飞机必须具有一定速度才可以获得能够克服自身重力的升力[2]。四旋翼无人机的空气动力结构使其能够实现定点悬停和垂直起降的功能。除此之外,四旋翼无人机还具有体积小、质量小、成本低、易操作、控制逻辑清晰等优点。四旋翼无人机的这些优势使得其在无人机市场占有相当大的席位,在军事侦察、管线巡逻、灾情监测、商业航拍等诸多领域都有应用价值[3]。

四旋翼无人机的广泛应用对其自身的性能提出了更高的要求,特别是姿态精度要求,所以对四旋翼无人机姿态的测量是无人机技术研究的重点。由于四旋翼无人机体积质量小,升力靠旋翼旋转产生,并且大多四旋翼无人机的动力来源都是机载电池,导致四旋翼无人机的升力和能源供应能力很有限[4]。传统的姿态测量系统由于体积、质量、功耗等原因,超过了四旋翼无人机的负载能力,因此寻找一种体积小、质量小、功耗低的姿态测量系统是四旋翼无人机技术研究的重点[5]。

随着科学技术的发展,基于微机械和微电子技术的微机电(MEMS)传感器被制造出来并广泛应用[6],微机电传感器体积仅为几毫米,质量为几毫克至几克,功率也仅为毫瓦级。因此基于微机电传感器的姿态测量系统就负载方面而言是四旋翼无人机的理想选择[7]。但是基于MEMS传感器的姿态测量系统除了存在陀螺漂移、积累误差、振动影响、外磁场干扰等误差外,还存在测量精度低的问题,这又对姿态的测量精度造成了影响。因此,四旋翼无人机负载能力与其姿态测量精度之间产生了矛盾,体积质量大、功耗高的传统姿态测量系统,不能满足四旋翼无人机的负载;而体积质量小、功耗低的微机电传感器组成的姿态测量元件又导致精度低。为了解决这个矛盾,本文研究一款基于微机电传感器的四旋翼无人机组合测姿系统,并结合数据融合的方法来提高测姿精度。

1 坐标系和姿态角描述

本文定义两种坐标系,分别是地理坐标系和机体坐标系。地理坐标系是载体所在地区的坐标系,常用符号n来表示。坐标原点通常为载体质心,定义z轴为当地地垂线方向并以指向天空为正向,x轴在当地水平面内以指向东为正向,y轴在当地水平面内以指向北为正向。

载体坐标系是固连在运动载体上的坐标系,常用符号b来表示。坐标原点通常选为载体质心,定义y轴沿载体对称线方向并以指向载体的前方为正,x轴垂直载体对称面并以指向载体右侧为正,z轴在载体对称面内以指向上为正。

姿态余弦矩阵表征了参考坐标系到载体坐标系的变换,反映了载体在参考坐标系中的姿态航向信息。

(1)

2 两种测姿方法

2.1 基于MEMS陀螺仪的测姿

MEMS陀螺仪为捷联式陀螺仪,没有陀螺环架,因此不能直接得到载体姿态信息,而需要对陀螺仪所测得的角速率进行积分来得到载体的姿态。利用捷联式陀螺仪测姿的解算方法有欧拉角法、方向余弦法、四元数法、等效旋转矢量法等,四元数算法所需参数少、计算简单、便于实现[8],所以本文采用四元数算法作为研究姿态角算法的基础。

四元数可表示为

Q=q0+q1i+q2j+q3k

(2)

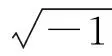
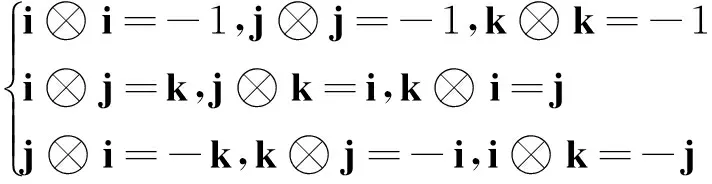
(3)

式中,⊗表示四元数乘法。

由四元数与坐标变换矩阵的关系,姿态余弦矩阵可由一个构成四元数的四个实数表示,表达式如下

(4)

这样,载体的姿态角就可由四元数表示为:

(5)

由于四旋翼飞行器飞行高度低,飞行速度慢,可以忽略地球自转等因素的影响,那么四元数具有如下微分方程关系[9]。

(6)

其中

ωx、ωy、ωz为三轴MEMS陀螺仪的输出。

设T为采样周期,四元数微分方程的一阶龙格-库塔法计算式为

(7)

只要知道每个周期的三轴MEMS陀螺仪的输出,就可以用式(7)迭代运算得到姿态四元数从而得到载体的姿态角。

2.2 基于MEMS加速度计和磁强计的测姿

当载体处于零加速运动的状态时,三轴加速度计的比力矢量和等于当地的重力加速度。如果此时载体水平,仅有天向加速度计有比力输出,并且大小等于重力加速度;而如果载体不水平,那三个轴的加速度计都会有输出,并且重力在三轴加速度计的分量与载体的姿态成一定的对应关系,可以表示为

(8)

f、gn分别表示三轴加速度计的比力矢量和当地重力加速度的比力矢量。结合姿态余弦矩阵,载体的俯仰角和横滚角就可以用三轴加速度计的比力输出表示:

(9)

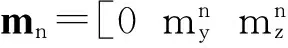
(10)

ψ=-arctan(mx/my)

(11)

3 基于Kalman滤波的姿态信息融合

3.1MEMS微惯性器件的误差建模

MEMS陀螺仪的误差种类繁多,在工程中对姿态解算精度影响比较大的主要有零偏误差、随机漂移误差、噪声等,也是建立MEMS陀螺仪误差模型的主要因素。MEMS加速度计的误差来源和种类与MEMS陀螺仪很相似,表述其性能好坏的主要性能指标有:零偏、零偏稳定性、线性度、噪声、随机漂移等等。磁强计的误差一般包括非正交误差、垂直轴效应误差、温度误差、零位误差和灵敏度误差等[6]。

在本文的研究中,将MEMS微惯性器件与磁强计的输出都看成是由理论值加上随机常数误差、一阶马尔科夫过程和高斯白噪声的综合[10]。

(12)

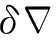
(13)

其中,TH、wh分别为MEMS微惯性器件漂移的相关时间和偏移噪声。

3.2 系统方程的推导

对四元数微分方程两边同时求导得到

(14)

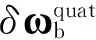
q-qg=δq

(15)

式中,q是载体姿态对应的真实四元数,qg是由陀螺仪单独测姿得到的四元数,本文选取两者的差作为系统的状态变量。

选取系统的状态变量为

X=[δq0,δq1,δq2,δq3,nbx,nby,nbz,nrx,nry,nrz]T

那么系统的状态方程可以表示成为

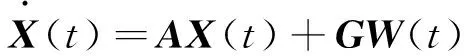
(16)

其中系统的过程噪声向量为

3.3 系统的观测方程

将加速度计和磁强计组合测姿得到的四元数与陀螺仪测姿得到的四元数作差得到的差值作为四元数误差的观测值,即

δqm=qm-qg

(17)

其中，qm是根据加速度计和磁强计组合测姿得到的四元数。

则系统的观测方程为

Z=δqm=HX(t)+V(t)

(18)

根据推导系统的状态方程和观测方程可以画出磁强计与微惯性器件的组合测姿系统的原理图如图1所示。

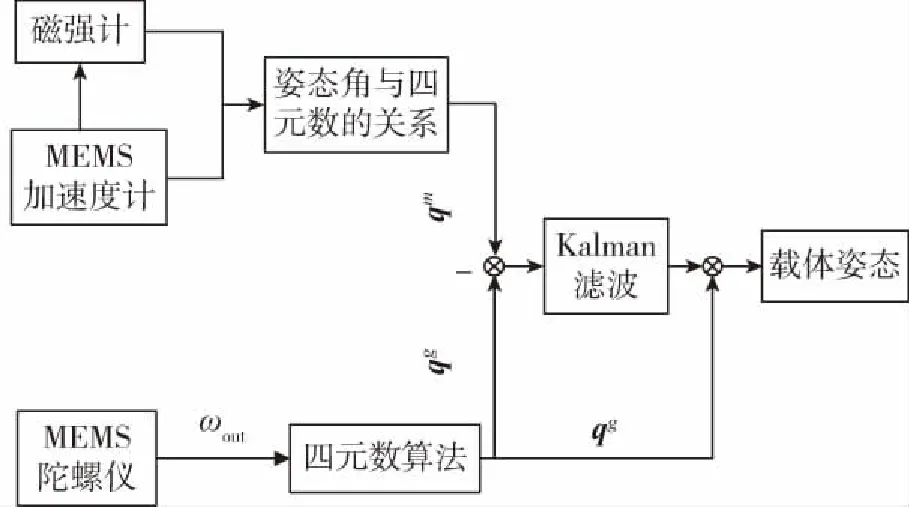
图1 组合测姿系统原理图Fig.1 Schematic diagram of integrated attitude determination system

3.4 仿真参数设置

3.4.1 传感器参数设置

传感器参数包括MEMS陀螺仪和加速度计以及磁强计的随机常数误差,一阶马科夫过程相关时间。传感器精度指标如表1[6]所示。

3.4.2 其他参数设置

系统状态初值x0,状态估计均方误差矩阵初值P0、系统噪声均方误差矩阵初值Q0和系统观测噪声均方误差矩阵R0初值设置如下:

x0=[0,0,0,0,0,0,0,0,0,0]

P0=diag([0.0022,0.0022,0.0022,0.0022,

(0.004(°)/s)2,(0.004(°)/s)2,

(0.004(°)/s)2,(0.004(°)/s)2,

(0.001(°)/s)2,(0.001(°)/s)2,

(0.001(°)/s)2])

Q0=diag([(0.004(°)/s)2,(0.004(°)/s)2,

(0.004(°)/s)2,(0.001(°)/s)2,

(0.001(°)/s)2,(0.001(°)/s)2])

R0=diag([0.0022,0.0022,0.0022,0.0022])

考虑到四旋翼无人机的续航时间,设置仿真时间为0.5h,姿态算法更新频率为 10Hz。

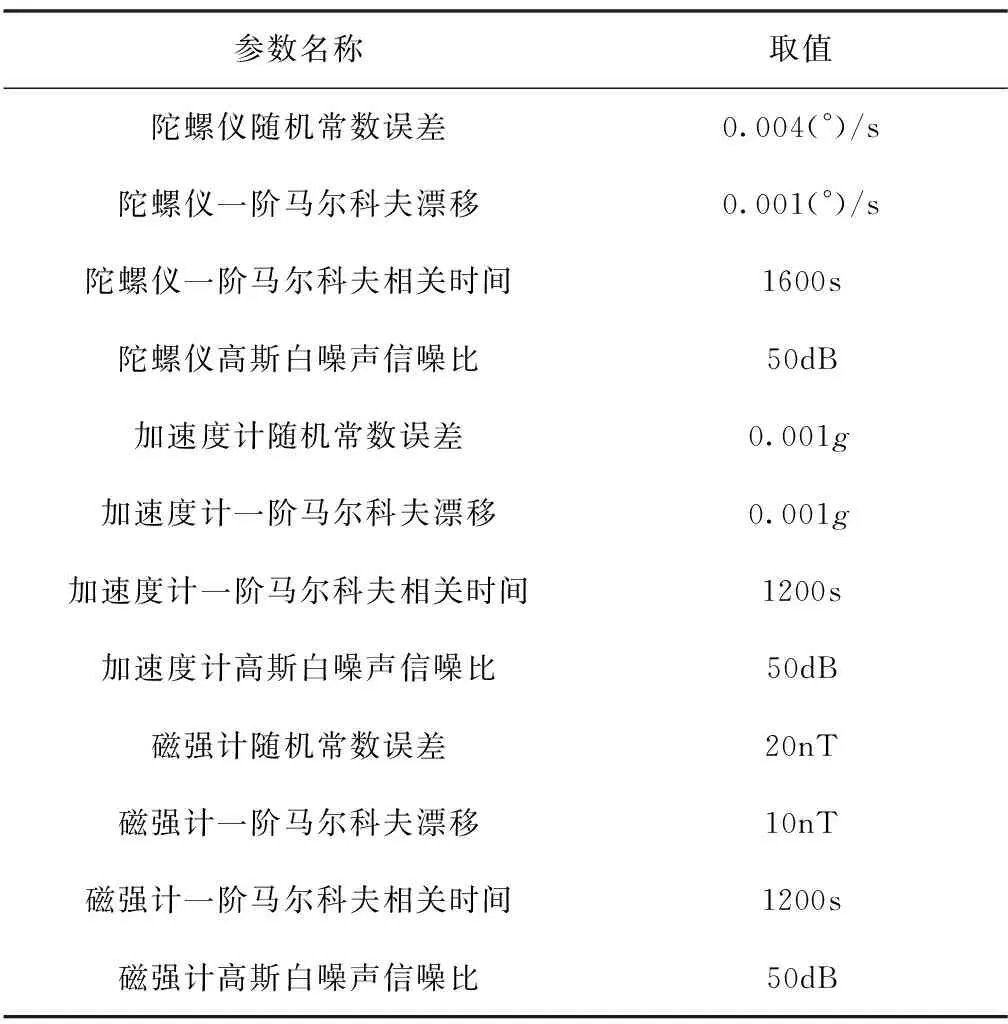
表1 传感器精度指标Tab.1 Accuracy of sensers

3.5 仿真与结果

在本文仿真分析中,假设载体做无加速度的运动,载体的3个姿态角按正弦规律变化为

(19)

分别利用MEMS陀螺仪单独测姿和利用MEMS陀螺仪、加速度计、磁强计组合测姿,并对两种测姿的精度进行分析,得到以下仿真图形如图2～图4所示。

由仿真图可以看出,单独利用MEMS陀螺仪测姿,由于MEMS陀螺仪的随机漂移和积累误差等原因,测姿精度低并且波动也比较大。而在融合进MEMS加速度计和磁强计后的组合测姿系统中,测姿精度得到了明显提高,实现了MEMS微惯性器件之间的性能互补。

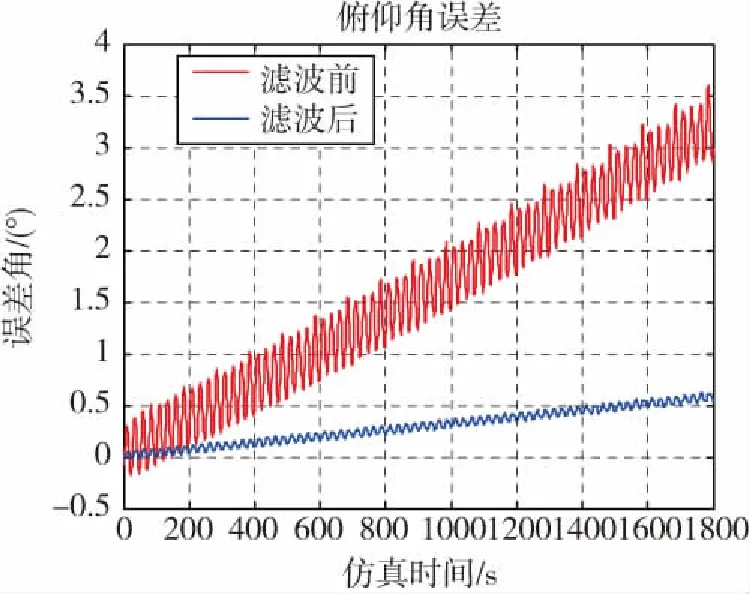
图2 俯仰角Fig.2 Pitch angle

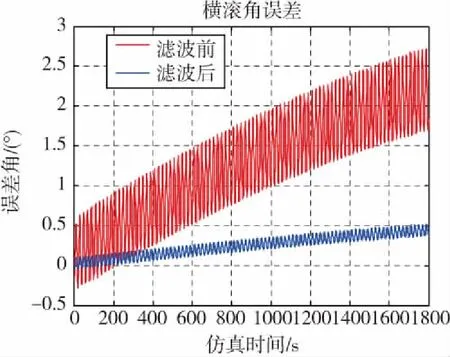
图3 横滚角Fig.3 Roll angle

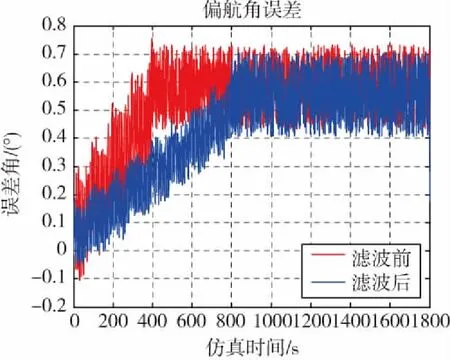
图4 偏航角Fig.4 Yaw angle

4 结论

本文充分利用四旋翼无人机上搭载的MEMS惯性器件,组成了两种测姿分系统。MEMS陀螺仪稳定性较好,但是具有精度低和积累误差的缺点,而MEMS加速度计和磁强计则没有积累误差,却容易受到外界环境的影响。通过Kalman滤波的方法将两种测姿系统所测得的姿态信息进行数据融合,通过仿真分析,验证了融合后测姿精度得到提高。

[1] 张浩, 任芊.四旋翼飞行器航姿测量系统的数据融合方法[J].兵工自动化，2013(1):28-31.

[2] 刘建业, 贾文峰, 赖际舟, 等.微小型四旋翼飞行器多信息非线性融合导航方法及实现[J].南京航空航天大学学报，2013，45(5):575-582.

[3] 宋英麟, 鲜斌, 茹滨超, 等.无人机微型姿态航向系统数据处理[J].中南大学学报(自然科学版)，2013(S2):89-93.

[4] 肖支才, 姜鹏, 戴洪德, 等.室内四旋翼无人飞行器定位导航的研究现状与关键技术[J].飞航导弹，2014(8):25-29.

[5] 汪绍华, 杨莹.基于卡尔曼滤波的四旋翼飞行器姿态估计和控制算法研究(英文)[J].控制理论与应用，2013，30(9):1109-1115.

[6] 伊程毅.基于地磁和微惯性器件组合的姿态测量系统研究 [D].哈尔滨工业大学， 2013.

[7] Skog I, Händel P.Calibration of a MEMS inertial measurement unit[J].Electrical Engineering Electronic Engineering Information Engineering，2007.

[8] 李会.基于地磁/低成本MEMS惯性器件复合姿态测量方法研究 [D].沈阳理工大学， 2014.

[9] 王凯, 马腾达, 周德新.基于多传感器融合的四旋翼飞行器姿态监控[J].测控技术，2015，34(3):21-24.

[10] 吴友强, 纪浩, 邹力涵.基于卡尔曼滤波的四旋翼飞行器悬停控制研究[J].自动化与仪表，2013，28(11):1-5.

[11] 马敏, 吴海超.基于四元数自补偿四旋翼飞行器姿态解算[J].制造业自动化，2013(23):18-21.

Research on Integrated Attitude Determination Methods Based on MEMS Device for Quadrotor UAVs

DAI Shao-wu1, LI Song-lin1, XING Zhi-chuan2, DING Guang-wei3, YUAN Peng4, KANG Yu-hang1

(1.Naval Aeronautical Engineering Institute, Yantai，Shandong 264001,China；2.The Troop of 91467, Qingdao，Shandong 266311,China；3.The Troop of 91206, Qingdao，Shandong 266108,China; 4.The Troop of 92330, Qingdao，Shandong 266001,China)

A micro attitude determination system is developed based on low-cost MEMS devices to meet the requirement for the flight control of micro unmanned aerial vehicles(UAV).But low-cost MEMS inertial devices have shortcomings such as low accuracy, great random drift, and is vulnerable to external environmental interference.In this paper,we make the full advantage of MEMS inertial devices equipped on Quadrotor UAV function,and realise data fusion of two attitude determination methods by Kalman filter.Through analysis of simulation, the attitude measurement accuracy of integrated attitude determination system has been improved.

Attitude determination system； MEMS inertial device； Kalman filter； Data fusion

10.19306/j.cnki.2095-8110.2017.03.005

2016-08-22；

2016-09-25

国家自然科学基金(61102167)；航空科学基金(21035184007)

戴邵武(1966-)，男，博士，教授，研究方向为导弹测试与控制。E-mail:dswhy@163.com

V249.122

A

2095-8110(2017)03-0027-05