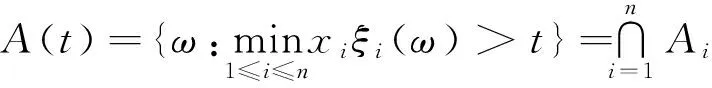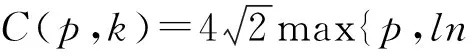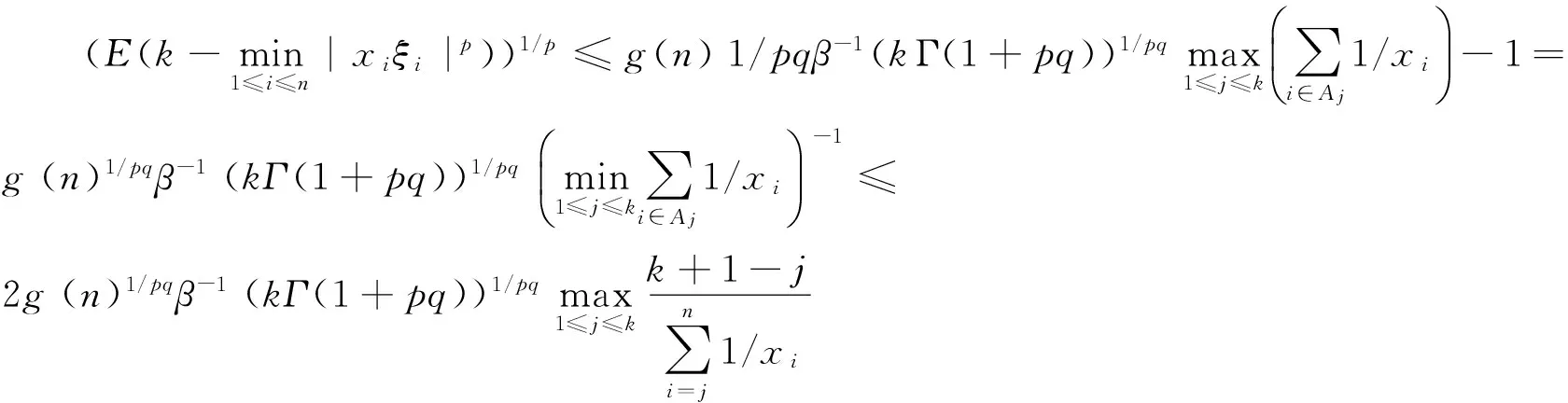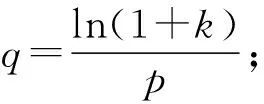非负WOD随机变量的第k小矩不等式

2017-05-11林君洁邓新鲍潇涵王学军

湖北大学学报(自然科学版) 2017年3期

关键词：安徽大学正数安徽

林君洁，邓新，鲍潇涵，王学军

(安徽大学数学科学学院，安徽合肥230039)

非负WOD随机变量的第k小矩不等式

林君洁，邓新，鲍潇涵，王学军

(安徽大学数学科学学院，安徽合肥230039)

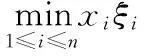
WOD随机变量; 矩不等式; 指数不等式

0 引言

P(|ξ|≤t)≤αt, ∀t≥0

(0.1)

P(|ξ|>t)≤e-βt, ∀t≥0

(0.2)

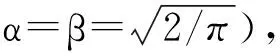
(0.3)

则称{Xn,n≥1}是WUOD随机变量; 如果存在一个有限的实数序列{gL(n),n≥1}, 使得对任意的n≥1及所有xi∈(-∞,+∞),1≤i≤n, 满足

(0.4)

1 相关结论

(1.1)

设x为一正数,Gamma函数定义为

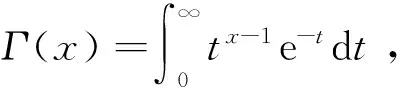
(1.2)

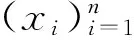
(1.3)

如果进一步假定ξ1,ξ2,…,ξn是独立的, 则

(1.4)

其中Γ(·)是Gamma函数. 定理B[2]设α>0,β>0,p>0,2≤k≤n. 设0

(1.5)

(1.6)

2 主要结果

(2.1)

其中g(n)=max(gU(n),gL(n)). 定理2.1的证明记

Ai(t)={ω:xiξi(ω)>t}={ω:ξi(ω)>t/xi},i=1,2,…,n,

P(Ai(t))≤e-βt/xi,i=1,2,…,n.由(0.3)式及上述不等式得,

(2.2)

定理2.2的证明不失一般性, 假定xi>0,i=1,2,…,n. 记

(2.3)

由定理2.1知

(2.4)

因此, 由(2.3)式和(2.4)式可得

(2.5)

特别地, 若{fn,n≥1}和{ξn,n≥1} 均为标准正态随机变量序列, 则对任意的n≥1, 有

(2.6)

推论2.1的证明由定理A知,

再由定理2.2和上面不等式可得,

定理2.3 设β>0,p>0,{xn,n≥1}为一非降的正数序列, {ξn,n≥1}为一个满足(0.2)式的非负WOD随机变量序列. 则对任意的n≥2和2≤k≤n, 有

(2.7)

因此, 由上述不等式及引理1得

定理得证.

[1]GordonY,LitvakAE,SchüttC,etal.Orlicznormsofsequencesofrandomvariables[J].AnnalsofProbability, 2002, 30: 1833-1853.

[2]GordonY,LitvakAE,SchüttC,etal.Ontheminimumofseveralrandomvariables[J].ProceedingsoftheAmericanMathematicalSociety, 2006, 134: 3665-3675.

[3]WangXJ,WangSJ,HuSH.Momentinequalityoftheminimumfornonnegativenegativelyorthantdependentrandomvariables[J].Filomat, 2014, 28(7): 1475-1481.

[4]LiuL.Preciselargedeviationsfordependentrandomvariableswithheavytails[J].StatisticsandProbabilityLetters, 2009, 79: 1290-1298.

[5]ChenY,ChenA,NgKW.Thestronglawoflargenumbersforextendnegativelydependentrandomvariables[J].JournalofAppliedProbability, 2010, 47: 908-922.

[6]ShenAT.ProbabilityinequalitiesforENDsequenceandtheirapplications[J].JournalofInequalitiesandApplications, 2011, 2011(1): 12.

[7]ShenAT.Onasymptoticapproximationofinversemomentsforaclassofnonnegativerandomvariables[J].Statistics:AJournalofTheoreticalandAppliedStatistics, 2013, 48(6): 1371-1379.

[8]WangYB,ChengDY.Basicrenewaltheoremsforarandomwalkwithwidelydependentincrementsandtheirapplications[J].JournalofMathematicalAnalysisandApplications, 2011, 384: 597-606.

[9]WangXJ,ZhengLL,XuC,etal.Completeconsistencyfortheestimatorofnonparametricregressionmodelsbasedonextendednegativelydependenterrors[J].Statistics:AJournalofTheoreticalandAppliedStatistics, 2015, 49(2): 396-407.

[10]EbrahimiN,GhoshM.Multivariatenegativedependence[J].CommunicationsinStatistics-TheoryandMethods, 1981, 10: 307-337.

[11]Joag-DevK,ProschanF.Negativeassociationofrandomvariableswithapplications[J].TheAnnalsofStatistics, 1983, 11: 286-295.

[12]WangXJ,HuSH,YangWZ,etal.ExponentialinequalitiesandinversemomentforNODsequence[J].StatisticsandProbabilityLetters, 2010, 80: 452-461.

[13]WangXJ,SiZY.CompleteconsistencyoftheestimatorofnonparametricregressionmodelunderNDsequence[J].StatisticalPapers, 2015, 56(3): 585-596.

[14]WuQY,JiangYY.ThestrongconsistencyofMestimatorinalinearmodelfornegativelydependentrandomsamples[J].CommunicationsinStatistics-TheoryandMethods, 2011, 40: 467-491.

[15]SungSH.Ontheexponentialinequalitiesfornegativelydependentrandomvariables[J].JournalofMathematicalAnalysisandApplications, 2011, 381: 538-545.

[16]QiuDH,ChangKC,GiulianoAR,etal.Onthestrongratesofconvergenceforarraysofrowwisenegativelydependentrandomvariables[J].StochasticAnalysisandApplications, 2011, 29: 375-385.

[17]ShenAT,ZhangY,VolodinA.Ontherateofconvergenceinthestronglawoflargenumbersfornegativelyorthant-dependentrandomvariables[J].CommunicationsinStatistics-TheoryandMethods, 2016, 45(21): 6209-6222.

[18]HuTZ.Negativelysuperadditivedependenceofrandomvariableswithapplications[J].ChineseJournalofAppliedProbabilityandStatistics, 2000, 16: 133-1440.

[19]ChristofidesTC,VaggelatouE.Aconnectionbetweensupermodularorderingandpositive/negativeassociation[J].JournalofMultivariateAnalysis, 2004, 88: 138-151.

[20]WangK,WangYB,GaoQW.Uniformasymptoticforthefinite-timeruinprobabilityofanewdependentriskmodelwithaconstantinterestrate[J].MethodologyandComputinginAppliedProbability, 2013, 15: 109-124.

[21] Wang Y B, Cui Z, Wang K, et al. Uniform asymptotic of the finite-time ruin probability for all times[J]. Journal of Mathematical Analysis and Applications, 2012, 390: 208-223.

[22] Liu X J, Gao Q W, Wang Y B. A note on a dependent risk model with constant interest rate[J]. Statistics and Probability Letters, 2012, 82: 707-712.

[23] He W, Cheng D Y, Wang Y B. Asymptotic lower bounds of precise large deviations with nonnegative and dependent random variables[J]. Statistics and Probability Letters, 2013, 83: 331-338.

[24] Shen A T. Bernstein-type inequality for widely dependent sequence and its application to nonparametric regression models[J]. Abstract and Applied Analysis, 2013(1): 9.

(责任编辑赵燕)

Moment inequalities of thek-minimum for nonnegative widely orthant dependent random variables

LIN Junjie，DENG Xin，BAO Xiaohan，WANG Xuejun

(School of Mathematical Sciences, Anhui University, Hefei 230039, China)