碳交易对碳排放数量影响的实证研究
2017-05-11刘钧炎
摘 要: 国内学者对碳交易的研究大多从宏观角度和制度层面阐述碳交易减少碳排放的原理;本文根据1990年至2015年广东省的碳排放数量、碳交易金额和地区生产总值,建立二元线性回归模型,探讨碳排放数量与碳交易金额之间的定量关系,并建立了ARIMA时间序列模型对广东省碳排放数量进行预测。
关键词:碳交易 碳排放数量 最小二乘法
中图分类号:F420 文献标识码:A 文章编号:1003-9082(2017)01-0100-02
一、文献综述
我国启动碳交易试点后,国内对碳交易的相关研究不断增加。国内学者对碳交易的研究大多从宏观角度和制度层面阐述碳交易减少碳排放的原理,如陈波从理论上阐述了碳交易的经济学原理,并介绍了欧盟碳交易机制的实践[1],李佐军等从理论上阐述了我国碳排放权的分配机制、交易机制和价格形成机制[2],郑爽等简要了介绍我国七个碳交易试点的制度和特点[3];国内也有一些学者对部分省市的碳排放的影响因素进行了定量研究,林珊珊基于江苏省1990-2013 年的数据,运用改进的 STIRPAT 模型分析了江苏省碳排放的影响因素,结论是技术进步对碳排放的抑制作用不显著,而经济增长和人口变动的作用较显著[4];黄蕊,王铮运用STIRPAT 模型对重庆市碳排放影响因素进行了定量分析,发现人口数量、人均GDP、能源强度、城市化水平与碳排放正相关、第三产业比重与碳排放负相关[5];国内学者很少对碳交易减少碳排放进行定量研究,本文将尝试进行定量研究,以广东省为例,建立二元线性回归模型,探讨碳排放数量和碳交易金额之间的定量关系。
如果碳交易确实对减少碳排放有积极的作用,那么如果发展华南地区碳交易市场,才能更好的减少碳排放?本文将进一步分析华南地区碳排放效率的差异,并以此提出发展华南地区碳交易的相关建议。
二、碳交易对碳排放效率影响的实证研究
1.模型构建
1.1碳交易对碳排放的影响
我国实行碳交易机制的目的就是依靠市场化手段实现强度减排和总量减排的双控目标,广东省碳交易试点在全国率先引入碳配额有偿分配机制,市场化手段分配碳配额的结果必然导致碳减排由高成本企业地区和转向低成本地区和企业,碳交易的总量和交易机制 (cap and trade system)同时也必然实现全社会碳排放的减少。为了定量研究碳交易对碳排放的影响,本文通过碳交易年度总成交金额来衡量粗略碳交易的发展程度,一般来说,碳交易年度总成交金额越高,表明碳交易越发达,碳排放数量应该越少,即碳交易年度总成交金额与碳排放数量成反比的关系。
1.2地区生产总值(GDP)对碳排放的影响
本文采取化石燃料产生的二氧化碳计算碳排放,而化石燃料占广东省一次能源消费总量的80%左右,能源消費总量又是地区生产总值必不可少的重要投入,所以碳排放与地区生产总值有着重要的相关关系。一般来说,地区生产总值越高,一次能源消费总量也越高,相应碳排放数量也越高,即地区生产总值与碳排放数量成正比的关系。
1.3地区生产总值和碳交易的关系探讨
碳交易市场是政府根据外部性原理强行创造出来的一个新市场,所以碳交易市场在诞生和成长过程中,影响最大的都是政策性因素;当地区生产总值较高时,碳排放数量也较高,但是碳排放数量高不一定导致碳交易金额高:一般来说,碳配额不足的企业会购买配额,碳配额多余的企业会出售配额,但是企业的碳配额充足与否与企业的碳排放数量无关,主要与企业自身的技术水平和碳交易政策等因素相关;所以,碳交易的金额主要与企业自身的技术水平和碳交易政策等因素相关,而与地区生产总值和碳排放数量关系不大,即碳交易总金额和地区生产总值没有显著的相关关系。
1.4初始碳排放的探讨
初始碳排放就是二氧化碳自发排放数量,当碳交易年度总成交金额和地区生产总值均等于零时,碳排放的初始值应该是一个正的常数,代表居民自发碳排放。
1.5模型构建
2.模型估计
2.1原始数据
数据来源。本模型的原始数据来源于《广东统计年鉴》和广州市碳排放权交易市场。
化石燃料数量的计算。化石燃料产生的二氧化碳占90%以上,所以本文中碳排放仅计算化石燃料产生的二氧化碳,化石燃料包括原煤、原油和天然气三种,这三种化石燃料的数据根据 《广东统计年鉴》中一次能源消费量查询得到;一次能源消费量的电力消费量包括水电、核电、风电、沼气发电、外省输入电力等,均不计算碳排放。
化石燃料排放系数的选用。根据国家统计局的数据,一万吨原煤折算0.7143万吨标煤,一万吨原油折算1.4286万吨标煤,一亿立方米天然气折算13.3万吨标煤;根据政府间应对气候变化委员会(IPCC)数据库,一万吨原煤产生的碳排放为1.9万吨,一万吨原油产生的碳排放为3.02万吨,一亿立方米天然气产生的碳排放为21.62万吨。所以,原煤的碳排放系数为2.66,原油的碳排放系数为2.11,天然气的碳排放系数为1.63。
碳排放数量的计算。化石燃料的数量乘以化石燃料的排放系数,可以得到化石燃料的碳排放,将三种化石燃料的碳排放加总,可以得到1990年至2015年的广东省碳排放总数量。
碳交易金额的计算。碳交易总金额包括《联合国气候变化框架公约》官方网站公布的广东省实际成交的清洁发展机制(CDM)项目(2006年广东出现第一个实际成交的CDM项目),还包括2013年及2014年广州碳排放权交易所的一级市场成交金额和二级市场成交金额。根据居民消费价格指数(CPI)核算出以1990年为基期的不变碳交易金额(2006年以前的碳交易金额为零)。
地区生产总值的计算。查询《广东统计年鉴》得到广东省地区生产总值的的当年值,以1990年为基期,根据居民消费价格指数,核算出以1990年为基期的不变GDP。
2.2模型估计
3.模型验证
3.1残差检验
通过检验残差的异方差性来检验模型。如果线性回归方程中的随机误差项满足假设条件中的同方差性,即多个因素不会随着自变量观测值的变化而对因变量产生不同的影响,就不会导致模型出现异方差性,那么参数估计就是有效的,参数的显著性检验就是有意义的。
对模型实施哈维检验(Heteroskedasticity Test: Harvey),收尾概率(Obs*R-squared)=7.9293,大于显著性水平5%,所以接受原假设,残差不存在异方差性,参数估计是有效的。
3.2参数检验
在1%的显著性水平上,a0、a1和a2的p值均小于0.01,说明公式(2)中的待估参数都在1%的水平上显著。
3.3模型整体检验
在1%的显著性水平上,F统计量对应的p值为0.0000,小于0.01,说明方程的整体线性是显著的;样本可决系数R2=0.9856,接近1,说明方程的拟合程度较好。
3.4模型的经济学验证
常数a0等于6907.548,即在碳交易金额和地区生产总值均为0的情况下,二氧化碳的自发排放数量为6907.548万吨,符合假设;系数a1等于–2.5684,即碳交易金额与碳排放数量成反比,以1990年为基期核算的碳交易金额对碳排放数量的影响系数为–2.5684,符合假设;系数a2等于1.7136,即地区生产总值与碳排放数量成正比,以1990年为基期核算的地区生产总值对碳排放数量的影响系数为1.7136,符合假设。
综合以上分析,该模型通过验证,可以根据广东省碳交易和地区生产总值来解释广东省碳排放,也验证了之前的模型假设:碳排放数量与碳交易成交金额成反比,广州碳排放权交易所的成交金额每上升10万元,广东省碳排放数量下降2.5684万吨;碳排放数量与地区生产总值成正比,广东省地区生产总值每上升1亿元,广东省碳排放数量上升1.7136万吨。
三、建立广东省碳排放数量的预测模型
本文拟建立碳排放数量的时间序列ARIMA模型,对广东省碳排放数量进行短期预测。
1.对广东省碳排放数量进行数列平稳化处理
广东省碳排放数量如上文所述,运用Eviews8.0对碳排放数量(y)做一阶差分的单位跟检验(无趋势项且无截距项),ADF检验的p值为0.0218,小于0.05,表示碳排放数量(y)的一阶差分是平稳数列,可以建立建立碳排放数量的时间序列ARIMA模型。
2.模型建立与识别
2.1通过自相关系数和偏自相关系数来确定模型的阶数p和q确定分析图中滞后阶数。滞后阶数k取[n/10]或[n/4](n为样本量,括号表示取整运算),本文中样本数n=25,所以滞后阶数k=[n/4]=6。
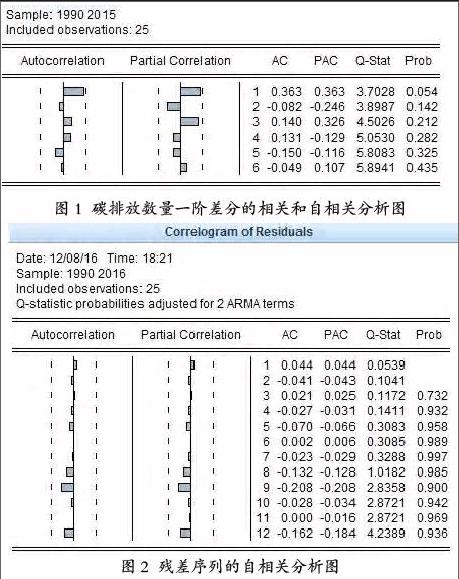
对碳排放数量的一阶差分进行相关和自相关分析(见图1),序列的樣本自相关与偏自相关系数很快落入随机区间,表明序列趋势已经基本消除,为平稳序列;偏自相关系数k=3后很快趋于0,因此取p=3;自相关系数在k=1处和k=5处显著不为0,可考虑取q=1和4。所以,广东省碳排放数量(y)可以建立ARIMA(1,3,0)预测模型或ARIMA(1,0,4)预测模型。
2.2选择ARIMA分析模型
当偏自相关系数k=3时,建立ARIMA(1,3,0)预测模型,即D(y) ar(1)。使用eviews8.0软件进行模型估计,ar(3)的P值为0.0131,说明变量在5%的水平下显著;模型滞后多项式的倒数根分别为0.80、-0.40+0.69i、-0.40-0.69,都落入单位圆内,模型满足过程平稳的要求。调整后的R方为0.2060,AIC值和SC值分别为18.3361、18.3857。
自相关系数在k=1和k=5时,建立ARIMA(1,0,4)预测模型,即D(y) ma(1) ma(4)。使用eviews8.0软件进行模型估计,ma(1)和ma(4)的P值分别为0.0000和0.0000,说明变量在1%的水平下显著;模型滞后多项式的倒数根分别为0.46-0.57i、0.46+0.57i、-0.81+0.54i、-0.81-0.54i,都落入单位圆内,模型满足过程平稳的要求。调整后的R方为0.2709,AIC值和SC值分别为17.7464、17.8439。
经过比较,ARIMA(1,0,4)模型的调整后的R方较大,且ARIMA(1,0,4)模型的AIC值和SC值较小,所以ARIMA(1,0,4)模型更合适,应选用ARIMA(1,0,4)模型对广东省碳排放数量进行预测。
3.模型检验
对ARIMA(1,0,4)模型的残差序列进行χ2检验,最大滞后期选12,使用eviews8.0软件对残差序列进行自相关分析(见图2),当k≤12时,残差序列的自相关系数都落入随机区间,且P值均大于0.05,表明残差序列是纯随机的,估计模型是有效的。
4.模型预测
根据ARIMA(1,0,4) 预测模型,使用eviews8.0软件对广东省2016年碳排放数量进行预测,结果为46061.08万吨。
参考文献
[1]陈波.碳排放权交易市场的设计原理与实践研究[M]. 北京:中国经济出版社,2014:3-50.
[2]李佐军等.中国碳交易市场机制建设[M]. 北京:中共中央党校出版社,2014:51-78.
[3]郑爽等.全国七省市碳交易试点调查与研究[M].北京:中国经济出版社.2014:250-275.
[4]林珊珊. 江苏碳排放的数量测算及其影响因素—基于改进STIRPAT模型的计量检验[J]. 南通大学学报(社会科学版),2015,31(4):9-16.
[5]黄蕊,王铮. 基于STIRPAT模型的重庆市能源消费碳排放影响因素研究[J]. 环境科学学报,2013,33(2):602-608.
作者简介:刘钧炎(1979-),男,河南许昌人,教研室主任,副教授,硕士,主要研究方向为区域经济与低碳经济。
