列车作用下高架车站内力分析及配筋研究

宋成辉

（中交铁道设计研究总院有限公司，北京 100097）

列车作用下高架车站内力分析及配筋研究

宋成辉

（中交铁道设计研究总院有限公司，北京 100097）

高架车站是建筑和桥梁综合体，承受列车动力作用。根据列车的实际编组和轮对，运用ANSYS APDL程序开展以下研究：（1）采用瞬态分析，计算钢轨磨损和接头不平顺条件下列车动力对高架车站的轨道梁、支撑柱的作用力，发现钢轨磨损下列车作用力影响较大；（2）以磨损不平顺为基础，分别计算列车运行时速60 km、80 km、120 km条件下对轨道梁、支撑柱的作用，结果表明列车运行时速越大，列车动力对轨道梁的作用力越大；（3）采用静力分析，将列车轴重乘以铁路设计规范计算动力系数按移动荷载施加在轨道梁上，计算结果与钢轨磨损条件下列车设计时速80 km计算完全一致；（4）将列车按均布荷载施加在轨道梁上，比较上述三者的差别，结果显示施加均布荷载造成轨道梁支座弯矩偏大、跨中弯矩偏小、支撑柱轴力偏大。根据列车作用下轨道梁内力分别以容许应力法和概率极限状态分析法进行配筋比较，两者配筋结果基本一致。

高架车站；瞬态分析；不平顺条件；耦合；荷载简化；内力分析；配筋

轨道交通高架车站是桥梁、建筑的综合体，采用2种规范体系《铁路设计规范》（简称铁规）和《建筑规范》（简称建规）[1]对列车-车站耦合进行计算并设计。GB 50157—2013《地铁设计规范》仅给出原则性指导意见，对列车-车站耦合的规律认识不清。对列车-车站耦合进行分析，找出耦合规律，以及列车荷载简化办法和存在的问题，为铁路高架车站设计提供借鉴。

1 工程概况及规范要求

本项目为桥-建合一高架站，岛式站台，横向4跨框架结构，纵向9跨，跨距12 m，横向跨支撑梁800 mm×1 500 mm，纵向跨站台梁6 000 mm×1 200 mm，次梁350 mm×800 mm，轨道梁400 mm×1 200 mm，并刚结在横向主梁和次梁上，每根轨道梁承载一条轨道，板厚200 mm（见图1）。GB 50157—2013《地铁设计规范》第10.6.9规定：横向三柱及以上的高架站采用建筑设计规范计算设计；第10.6.10规定：横向单柱和双柱结构应按铁路设计规范计算设计。本项目为四柱三跨结构，轨道梁刚接站台梁，采用建规设计，但对轨道梁及其支撑体系按区间铁规进行设计[2-4]。

对列车竖向荷载作用下高架车站行车梁的受力进行分析，并对比2种规范下的配筋计算。但对于认识比较成熟的地震、风载、温度等荷载作用下响应及设计不再讨论。

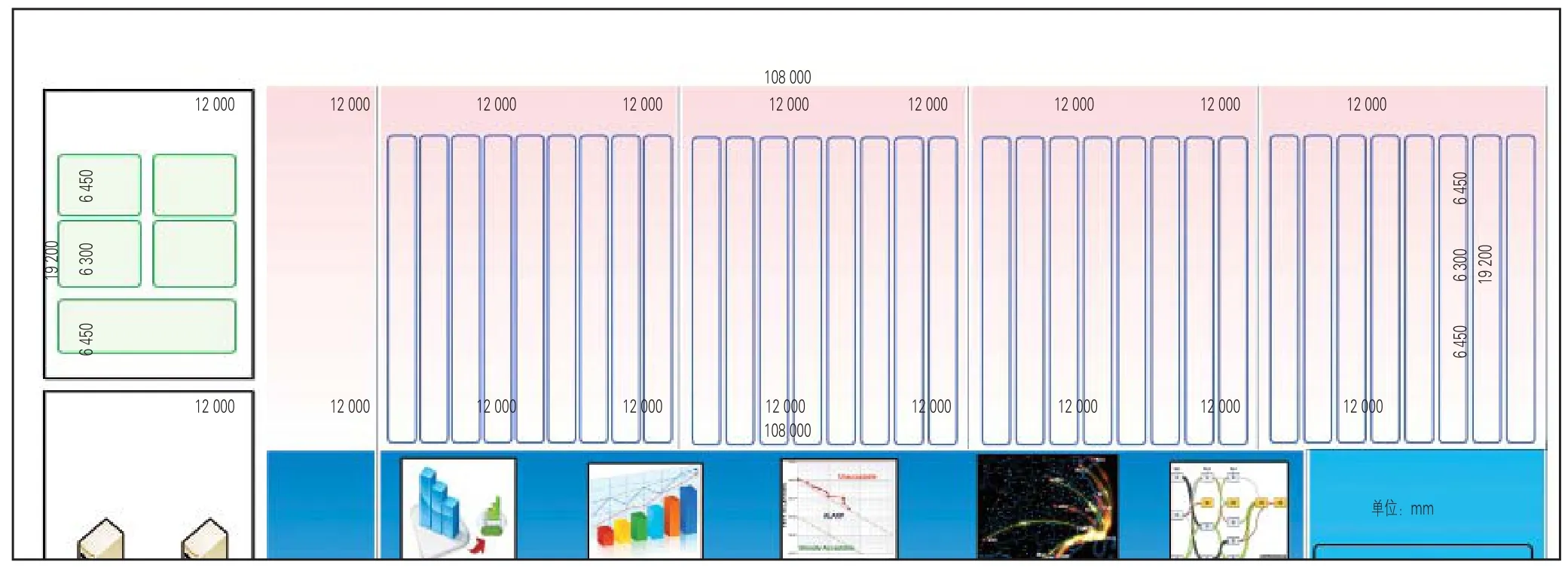
图1 行车层结构平面示意图

2 动力耦合

列车-车站耦合计算中，列车车轮对轨道梁的冲击为变化荷载，且荷载在车站轨道梁的位置随列车运行变化，因此列车-车站耦合计算可采用瞬态计算，计算车站轨道梁在列车运行状态下的动力学响应。瞬态计算的方程：

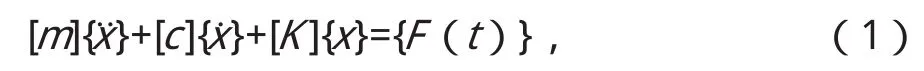
式中：[c]为阻尼矩阵；[m]为质量矩阵；[K]为刚度矩阵；{ F（t）}为载荷向量；为速度向量；为加速度向量。

2.1 列车竖向荷载振动方程

查阅国家自然科学基金重点项目“城市轨道交通引起的环境振动与传播规律（基金编号：50538030）”的研究成果[5]，该项目对北京城轨13号线回龙观—霍营段列车运行引起的振动进行观测。得出由于轨道接头和焊接使钢轨走行面发生局部不平顺、轮周面局部擦伤和偏心轮重、轨枕支承面刚实程度不同的影响，列车荷载所引起的钢轨、衬砌及周围介质的振动属于随机振动。为了得到轮轨振动荷载，可采用轮轨系统激励，例如：谐波激励；也可采用轨道谱，如中南大学的轨道谱、中国铁道科学研究院的轨道谱，或人工合成时程谱，如三角级数法[6]。

轨道几何状态不平顺可用单个或多个简谐波来近似描述，为了简化计算采用正（余）弦函数来描述简谐激励。轨道不平顺简谐振动方程[5]：

根据竖向动力平衡条件，得到轮轨间相互作用力：

式中：ω为钢轨振动圆频率，ω=2πv/L；v为列车速度，km/h；L为振动波长，短波取1 m，中波取钢轨长度12.5 m；α为不平顺振幅，磨损振幅状态下取0.3 mm，接头高差不平顺振幅取0.8 mm；φ为钢轨振动相位角，为了简化计算取相位角为0°；m为列车轮重换算的质量，取7 t；P0为轮静载，取70 kN；t为荷载作用时间。

2.2 列车荷载和编组

根据GB 50157—2013《地铁设计规范》，单线和双线高架结构应按列车活载作用于每一条线路确定。本项目研究按B型车6节编组，单列纵向最大轴重按140 kN取值（见图2）。

图2 列车轴重模式

2.3 轮轨作用受不平顺影响分析

轨道随机不平顺波长范围较广，根据波长分为短波不平顺、中波不平顺和长波不平顺。其中短波不平顺（一般波长小于1 m）激振频率高对轮轨相互作用力、轮重减载率以及轮轨噪声产生明显影响，而对列车车体振动加速度及乘坐舒适性影响甚微；中波不平顺（波长1～30 m）主要对列车运行平稳性及舒适性产生影响，而对行车安全性及轮轨动力作用影响较短波不平顺小；长波不平顺（波长30～200 m）则对提速或高速列车运行舒适性产生重要影响。短波不平顺主要受轨道磨蚀影响；中波不平顺受轨道接头、钢轨加工误差、轨枕的施工等因素影响；长波不平顺受线路、路基施工等因素影响[7-9]。根据式（5）得出波长越短引起轮轨作用力越高，此次主要研究列车荷载作用影响，因此对磨蚀引起的短波和钢轨接头高差引起的中波进行分析。

模拟列车编组和轮对，以列车设计时速80 km荷载加载轨道梁上，考虑最不利组合：列车双向对开，同时、同步驶过车站。分别按2种中短波进行分析：第一种情况为短波，根据《铁路线路修理规则》（铁运［2006］146号）第3.4.3条，钢轨磨蚀按L=1 m、磨蚀a=0.5 mm；第二种情况，根据GB 2585—2007《铁路用热轧钢轨》第5.1.2条规定，钢轨接头允许高差取0.8 mm；L为钢轨振动不平顺波长，每根钢轨取L=12.5 m。

根据式（5）计算磨损情况下单轮对轨道梁的冲击力方程：

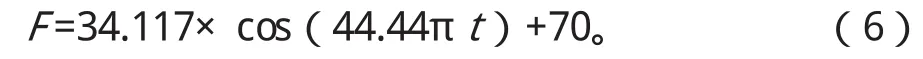
根据式（5）计算接头高差不平顺情况下单轮对轨道梁的冲击力方程：

按6辆车编组，根据列车速度和网格划分间距，以时间t不同作用不同轨道梁上节点，列车运行过程在轨道梁上作用采用ANSYS APDL程序进行编程计算（见图3），图中箭头表示列车车轮作用在轨道梁上的荷载，荷载间距为列车轮间距。

计算右线左行车梁的弯矩、剪力包络线见图4、图5。

图3 对开列车行驶在车站中部轴重荷载

图4 不平顺条件下行车梁的弯矩包络线

图5 不平顺条件下行车梁的剪力包络线

从图4、图5可以看出，行车梁结构内力主要受短波影响较大，即钢轨磨蚀对轮轨作用影响较大，因此磨损不平顺对列车起控制作用。安全起见，以下动力分析都以磨损不平顺条件为基础，分析列车在不同设计速度下轮-轨的作用响应。

2.4 轮轨作用受列车速度影响分析

根据式（5）得出列车运行速度越大引起轮轨作用力越高。在磨损不平顺情况下，列车分别以时速60 km、80 km、120 km运行，3种速度下车轮对轨道梁的冲击力方程如下：

3种速度运行分析结果比较见图6、图7。

从图6、图7可以看出，行车梁结构内力主要受行车速度影响较大，行车速度越高，轮轨作用影响越大。本项目城市轨道交通设计时速为80 km，因此后面静力分析结果均与设计时速80 km动力分析结果相比较。

图6 不同行车速度行车梁的弯矩包络线

图7 不同行车速度行车梁的剪力包络线

磨损不平顺条件下，当行车时速80 km时，以轨道梁第5跨中节点挠度作为监测点，以整个列车通过该高架站作为时间历程，轨道梁跨中节点挠度时间历程曲线见图8。

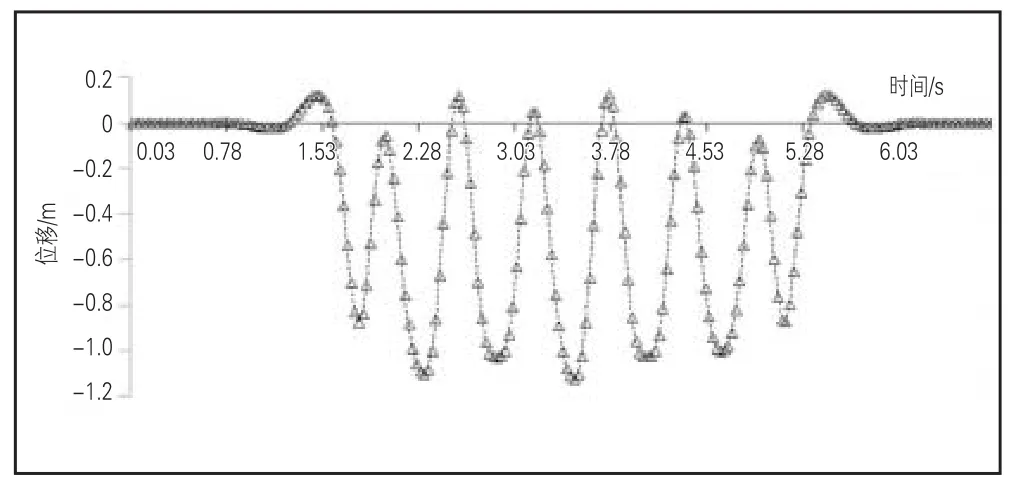
图8 短波行车速度120 km/h行车梁跨中位移影响线

根据图8可知，列车同步对开位于中间位置时，行车梁挠度最大。

3 静力下移动荷载与动力耦合分析比较

静力下移动荷载计算，不考虑列车和车站动力耦合效应，将列车轮重乘以动力系数并根据固定轴距排列后以移动方式加载行车梁各个对应位置，即：荷载恒定，但荷载位置随时间在轨道梁上移动。计算结构在不随时间变化，而随荷载位置变化工况下，移动荷载静力计算公式：

式中：{F（x）}为位置不断变化的荷载向量；[K]为刚度矩阵；{c}为变形向量。

列车竖向活载的动力系数为（1＋μ），μ按现行《铁路桥涵设计基本规范》规定的值乘以0.8。

式中：对于整体无砟道床，a取2；L为最大桥跨，取12 m。

根据图8换算轮重乘以动力系数按实际6辆车编组和轮距将荷载以移动形式加载于行车梁上，计算梁内力包络线，并与列车时速80 km时列车-车站耦合分析内力包络进行比较，比较结果见图9—图12。

图9 速度80 km/h与移动荷载行车梁弯矩包络比较

图10 速度80 km/h与移动荷载行车梁剪力包络比较

图11 速度80 km/h与移动荷载角柱轴力变化曲线比较

图12 速度80 km/h与移动荷载中柱轴力变化曲线比较

根据图9—图12，在设计时速80 km、短波不平顺条件下动力耦合分析结果与采用动力系数乘以列车轴重排列以移动静力分析结果基本一致。计算结果如下：行车梁跨中最大弯矩170 kN·m；支座弯矩最大值200 kN·m，行车梁支座剪力150 kN；框架柱角柱轴力最大250 kN，中间柱轴力约250 kN。

4 按均布荷载分析

利用软件PKPM设计计算，将列车荷载按静力均布荷载加载在轨道梁上，计算结果与列车-车站耦合、静力下移动荷载计算进行比较。均布荷载按“列车满载+车自质量/列车长度”得到线性值29.84 kN/m，再乘以动力系数加载在行车梁上，得到内力图（见图13—图15）。

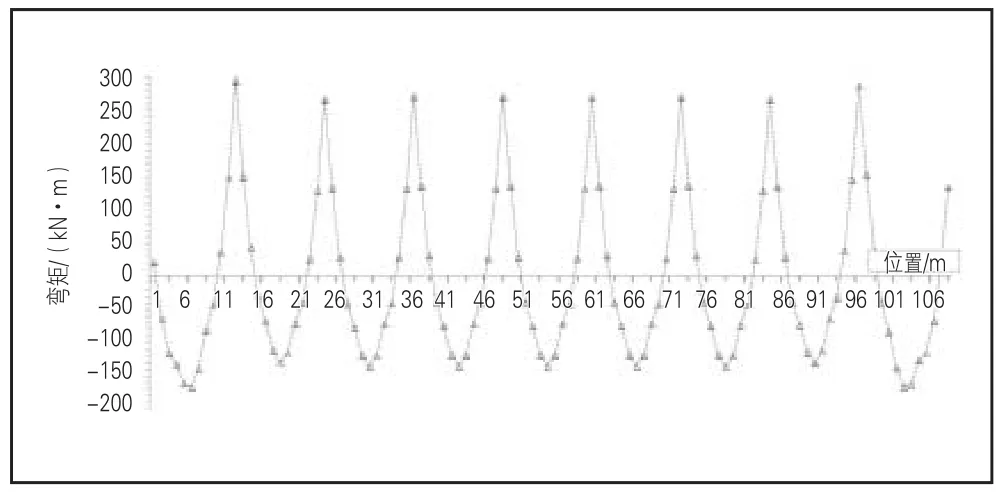
图13 满布均布荷载行车梁弯矩

图14 满布均布荷载行车梁剪力

图15 满布均布荷载车站柱轴力

根据图13—图15分析，均布荷载作用下行车梁最大跨中弯矩165 kN·m，支座弯矩约300 kN·m；行车梁支座剪力约150 kN；框架支撑柱，角柱轴力约293.2 kN，长边边柱轴力约536.6 kN，中间柱轴力约414.9 kN。

列车在短波不平顺、设计时速80 km条件下，车-桥耦合计算结果、按铁路规范动力系数乘以轴重移动荷载静力分析结果及按列车满载条件下，动力系数乘以均布荷载施加轨道梁上计算结果对比见表1。

表1 动载耦合、移动与均布荷载车站构件内力对比

根据表1得出，以动力系数乘以均布荷载29.84 kN/m施加行车梁上以取代列车荷载，计算结果为：行车梁支座弯矩增大约50%；跨中弯矩减小约3%；角柱增大约17%；中间支柱增大约65%。

5 容许应力法与概率极限状态法配筋比较

根据GB 50157—2013《地铁设计规范》，桥建合一行车梁按TB 10002.3—2005《铁路桥涵钢筋混凝土和预应力混凝土设计规范》容许应力法进行设计配筋；而建筑规范采用GB 50010—2010《混凝土结构设计规范》概率极限状态分析法计算配筋。为了理解这2种规范差别，对承受列车荷载的行车梁分别按容许应力和概率极限状态分析法进行配筋比较。根据以上分析，移动荷载计算行车梁的跨中弯矩170 kN·m，根据该计算结果分别以极限状态分析法配筋、容许应力法配筋进行比较。其中行车梁采用C40混凝土，保护层厚度25 mm。

5.1 概率极限状态正截面受弯配筋计算

概率极限状态配筋采用基本组合活载，分项系数采用1.4，列车活荷载引起行车梁跨中弯矩基本组合后为238 kN·m。

行车梁受压区高度：

计算普通钢筋面积：

式中：x为受弯构件受压区高度，mm；h0为预应力梁截面有效高度，mm；M为荷载组合弯矩值；γ0为结构重要系数，取1.1；b为预应力梁宽；a1为调整系数；fc为混凝土轴心抗压强度设计值；As为受拉普通钢筋截面积，mm；fy为纵向受拉钢筋受拉强度设计值。

由计算可知，可配2φ25HRB400钢筋。

5.2 受弯构件容许应力配筋计算

容许应力计算配筋采用标准组合计算弯矩，列车活荷载引起行车梁跨中弯矩170 kN·m。

用概率计算钢筋面积，As=637.6 mm2，钢筋与混凝土弹性模量比：

支撑梁400 mm×1 200 mm，b=400 mm，h=1 200 mm，保护层厚度25 mm，考虑在有自质量、道床、轨道等荷载作用下，往往实际配2排φ25 mm钢筋，h0=1 125 mm，仅列车活荷载弯矩M=170 kN·m。

受压区高度：

截面惯性距：

受压区混凝土应力：

受拉区钢筋应力：

式中：σc为混凝土压应力，MPa；σs为钢筋拉应力，MPa；[σb]为混凝土受压容许应力，C40混凝土取13.5 MPa；[σs]为钢筋容许应力，HRB400容许应力取300 MPa；M为计算弯矩，MN·m；n为钢筋弹性模量和混凝土弹性模量比，采用多层钢筋计算最外层钢筋应力；b为梁宽；h0为梁有效高度；As为受拉区钢筋面积；x为梁受压区高度，mm；I0为截面有效惯性距，m4。概率计算配筋面积完全满足容许应力配筋要求。

6 结论

（1）磨损不平顺引起轮轨作用力最大；列车时速越大，轮轨作用越大；采用均布荷载近似加载计算，梁支座负弯矩偏大，跨中正弯矩偏小，柱轴力偏大，中部柱轴力过大。采用车-桥耦合动力分析与按铁规动力系数乘以轴重以移动荷载的静力分析基本一致。

（2）容许应力法配筋以材料为弹性材料，而概率极限以塑性理论为基础。概率极限分析法和容许应力法相比，用多系数取代单一系数，容许应力法的设计荷载等于荷载标准值组合，而概率极限法的设计荷载是荷载标准值与结构重要性系数、荷载分项系数、可变荷载的组合系数的一个组合值。采用概率极限配筋能够满足铁路规范配筋要求。

[1] 许小波. 铁路桥梁规范和建筑规范在城市轨道交通高架车站结构设计中的应用[J]. 城市轨道交通研究，2014(9)：128-130.

[2] GB 50157—2013 地铁设计规范[S]．

[3] TB 10002.1—2005 铁路桥涵设计基本规范[S].

[4] GB 50011—2010 建筑抗震设计规范[S].

[5] 崔高航. 城轨交通引起的环境振动研究及轨道谱参数虚拟反演[D]. 哈尔滨：哈尔滨工业大学，2009.

[6] 李小珍，刘全民. 铁路高架车站车致振动实测与理论分析[J]. 西南交通大学学报，2014，49(4)：613-618.

[7] HIROKAZU TAKEMIYA, SHUEHI SATONAKA, WEI-PING XIE. Train track-ground dynamics due to high speed moving source and ground vibration transmission[J]. Journal of Structure Mechanics and Earthquake Engineering, 2001, 682(7): 299-309.

[8] X TAO，X ZHENG，Q XING. Virtual inversion of environment vibration sources caused by rail traffic in urban areas[C]//The 14th International Conference on Urban Transport and the Environment in the 21st Century, Malta, 2008.

[9] 陈宪麦. 轨道不平顺时频域分析及预测方法的研究[D]. 北京: 铁道科学研究院，2006.

责任编辑 李葳

On Internal Force and Reinforcement of Elevated Stations Under Train Dynamics

SONG Chenghui
（CCCC Railway Consultants Group Co Ltd，Beijing 100097，China）

Formed by buildings and bridges, the elevated station, as a whole, bears train dynamics. According to the actual train formation and wheelsets, ANSYS APDL program is used for the following study: the transient analysis is applied to calculate the acting force of train dynamics on track beams and supporting pillars of the elevated station under the conditions of rail wear and joint irregularity. It is found that with rail wear, the effect of the train's dynamics is relatively high. Based on irregularity of rail wear, the effect of train dynamics on track beams and supporting pillars with the train running at speed of 60km/h, 80km/h and 120km/h is calculated respectively. The results show that the acting force of trains on track beams increases with the speed of the train in operation; static analysis is used while the axle load of the train is multiplied by the dynamic coeff cient calculated in accordance with railway design specif cations to obtain the moving load, which is then applied to the track beam. The calculation result is exactly the same with that acquired under the design speed of 80 km/h with rail wear. The load of the train is then simplif ed as an even load, which is exerted on the track beam. The three cases above are compared with each other and the results show that, under the even load, the bending moment of the track beam support is relatively large, the mid-span moment is relatively small, and the axial force of the supporting pillar is relatively large. According to the internal force of the track beam under train dynamics, the reinforcement results obtained with the allowable stress method and the probabilistic limit method are compared with each other, which are found to be basically the same.

elevated station；transient analysis；irregular condition；coupling；load simplif cation；internal force analysis；reinforcement

TU311.3；TU248.1

A

1001-683X（2017）01-0071-07

10.19549/j.issn.1001-683x.2017.01.071

2016-10-07

国家自然科学基金资助项目（41272352）

宋成辉（1970—），男，高级工程师，博士。E-mail：729887000@qq.com