坐标转换理论及其在半实物仿真姿态矩阵转换中的应用*

陈 凯,王 翔,刘明鑫,于云峰,闫 杰

(西北工业大学航天学院,陕西 西安 710072)



坐标转换理论及其在半实物仿真姿态矩阵转换中的应用*

陈 凯,王 翔,刘明鑫,于云峰,闫 杰

(西北工业大学航天学院,陕西 西安 710072)

以临近空间飞行器半实物仿真试验需求为背景,利用坐标转换理论推导了航空和航天两种体系下姿态矩阵的关系。首先,介绍了坐标转换理论,包括两种直角坐标系之间的转换关系,以及两种不同参考系下的姿态矩阵转换关系。然后,分析了航空和航天体系下坐标系之间的关系,推导了从航天体系下姿态矩阵到航空体系下姿态矩阵的转换关系。半实物仿真试验表明,推导的方法正确可行,保证了临近空间飞行器导航系统的仿真验证。

坐标转换;姿态矩阵;半实物仿真;捷联惯性导航;临近空间飞行器

半实物仿真是一种硬件在回路的仿真方法,半实物仿真系统将所研究系统的部分实物接入到仿真系统回路,使之成为仿真系统的一个组成部分[1]。飞行器半实物仿真的目的是将飞行器飞行控制系统接入半实物仿真系统中,在地面实验室条件下尽可能逼真地复现飞行器在空中的飞行环境,验证和评估飞行器飞行控制系统性能指标,缩短项目开发流程、降低外场试验风险、节约项目成本[2]。图1是典型的飞行器飞控半实物仿真系统,主要包括半实物仿真设备和弹上设备[3]。半实物仿真设备包括:实时仿真机系统、飞控系统性能分析系统、三维视景系统、数据显示记录系统、负载模拟器、SAR图像模拟器(或末制导模拟器)、产品接口系统、三轴转台、导航信息模拟器、卫星模拟器等;弹上设备包括:舵机、SAR(或末制导设备)、弹载机、IMU/GPS等。根据不同的飞行器,半实物仿真系统将有所增减。

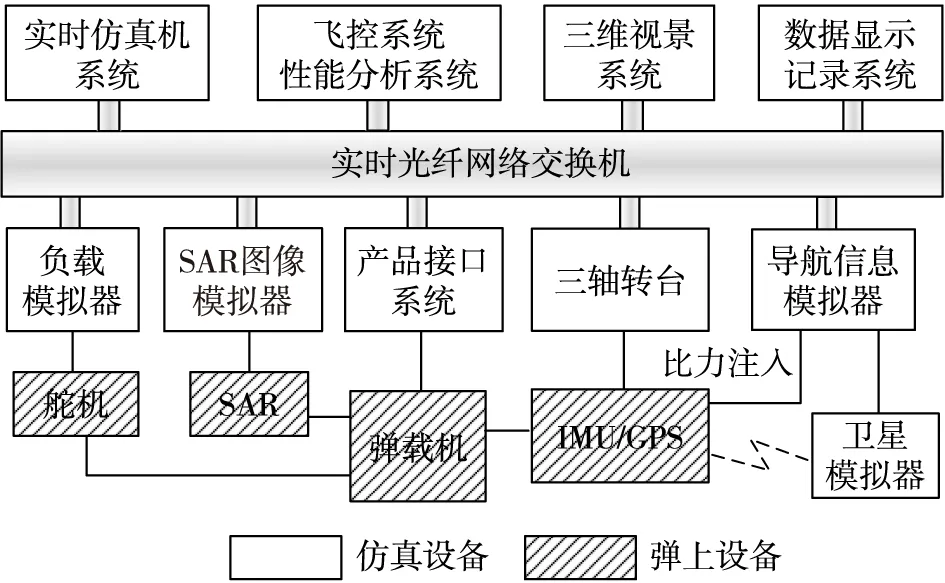
图1 飞行器飞控半实物仿真系统

如图1所示,在半实物仿真中,实时仿真机系统运行飞行器六自由度动力学和运动学模型,实时计算飞行器的位置和姿态、所受的力和力矩,并为三轴转台提供姿态角指令,三轴转台是飞行器姿态运动仿真设备;导航信息模拟器和卫星模拟器模拟飞行过程中的比力和卫星信号;负载模拟器根据弹载机的舵控指令,模拟飞行过程中舵机所受的力矩。半实物仿真中,存在飞行器飞行力学、飞行控制与制导、导航技术、仿真技术等多个学科的交叉;半实物仿真试验过程也是多个学科对接和融合的过程。临近空间飞行器的飞行高度一般在20km～100km,介于航天和航空邻域之间。随着临近空间飞行器的研究,飞行器飞控半实物仿真系统逐步打破了航天和航空邻域的界限[1]。其中,飞行器的位置、速度和姿态信息,存在航天和航空两种体系的表示方式。在航天体系中,以发射点坐标系(发射坐标系/发射惯性坐标系)为参考坐标系,描述飞行器的位置、速度和姿态信息[4];半实物仿真的六自由度模型的位置、速度和姿态信息,也是建立在发射点坐标系下[5]。在航空体系中,以当地水平坐标系为参考坐标系,描述飞行器的位置、速度和姿态信息[6]。为了进行飞行器半实物仿真试验,需要在两种体系间进行位置、速度和姿态的相互转换,典型的共性需求包括:1)半实物仿真的六自由度模型以发射点坐标系为参考,而飞行器的导航算法使用当地水平坐标系,需要分析二者关系;2)六自由度模型需要为卫星模拟器注入相对当地水平坐标系下的相关信息;3)飞行器再入段的图像模拟,六自由度模型需要提供飞行器相对当地水平的姿态信息。刘敏研究了在组合导航系统半实物仿真中位置信息的发射地面坐标系和地理坐标系位置信息的相互转换[7]；袁智荣研究了当地水平坐标系到发射坐标系的位置、速度、航姿角的转换关系[8]；吴盘龙研究了精确制导炸弹在飞行过程中不同坐标系间的转换关系[9]；秦玉亮研究了SAR导引头位置转换问题[10]；Zhao H T研究了地图投影中不同坐标系间的转换关系[11]。

位置在三维空间由质点表示,速度在三维空间由矢量表示,半实物仿真中的相互转换相对容易;而姿态是由飞行器相对参考坐标系的三次旋转得到,采用三个姿态角表示,既不是质点,也不是矢量,半实物仿真中的相互转换相对困难,很少有文献涉及。文献[5]介绍了坐标转换方法,实现了临近空间高超声速飞行器发射坐标系下的导航信息转换到当地水平导航坐标系下方法,但是姿态角相关的坐标转换理论基础和转换过程并没有详细介绍。本文根据半实物仿真试验的要求,首先介绍坐标转换理论,然后推导了从航天体系下姿态矩阵到航空体系下姿态矩阵的转换关系,最后进行半实物仿真验证。

1 坐标转换理论

1.1 坐标转换理论介绍

在同一参考坐标系下,由于三次姿态角旋转顺序的不同,理论上有24种旋转方法,存在24种姿态矩阵的表示形式。不同国家、不同领域,使用的参考坐标系习惯不同,存在着更多的姿态表示方法。然而,不管姿态如何变化,都可以用坐标转换理论进行解释。其简介如下:空间任意两个坐标系之间的指向,均可通过坐标系依次绕坐标轴旋转使两者在空间的指向一致。而每一次绕自身某一轴旋转后的坐标系和原坐标系可以用方向余弦阵联系起来[12-13]。

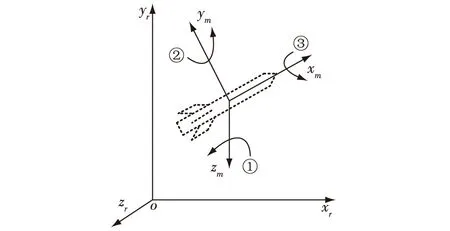
图2 姿态角定义图

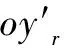
(1)

其中:

(2)

(3)

(4)

由此,得到了由参考坐标系到飞行器坐标系的一种姿态矩阵形式。

1.2 两种直角坐标系的转换关系

如图3所示,参考坐标系oxRyRzR(R系)与参考坐标系oxryrzr(r系)的三轴平行,但是指向不同。通常,R系称为“右前上”坐标系,为航空中常用坐标指向;而r系称为“前上右”坐标系,为航天中常用坐标指向。R系至少需要通过两次坐标转换,转换为与r系指向完全一致。共存在3种变换,且结果相同。分别是:

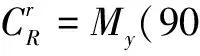
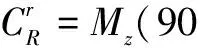
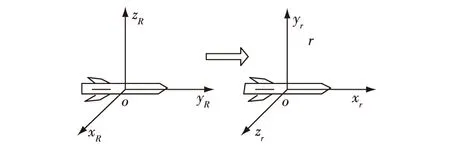
图3 两种直角坐标系的转换关系

1.3 两种参考系下的姿态矩阵转换关系

通过坐标转换理论,可以分析两种不同参考坐标体系下姿态矩阵之间的关系。如图4所示,在r系和m系的基础上,增加oxRyRzR参考坐标系(R系)和oxMyMzM弹体坐标系(M系)。R系和M系为“右前上”坐标系,而r系和m系称为“前上右”坐标系,二者指向不同。

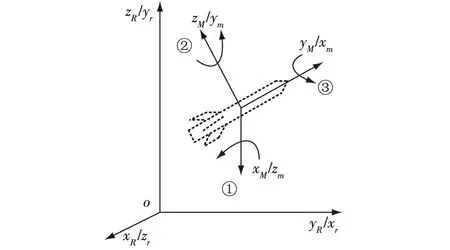
图4 两种体系下姿态角定义图

按照图2的旋转,R系同样按照先俯仰α、再偏航β、最后滚转γ的顺序,得到的姿态矩阵为

(5)

虽然飞行器在空间的实际指向相同,由于参考坐标系和弹体坐标系定义的空间指向不同、所绕坐标轴也不同,由于旋转的不可交换性,因此

(6)

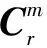
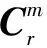
因此,将R系旋转至M系,可通过式(5)所示的3次旋转得到,也可通过上述的7次旋转得到,描述如下:

(7)

2 半实物仿真中两种姿态矩阵关系

临近空间飞行器半实物仿真中涉及的姿态角主要分为两大类°1)以发射点坐标系(本文采用发射惯性坐标系)为参考系的飞行器姿态角定义,这类通常是航天体系和飞行器六自由度模型下的姿态角,一般以“前上右”为参考坐标[4-5];2)以当地水平坐标系为参考的飞行器姿态角定义,这类通常是航空体系下的姿态角,国内一般以“右前上”为参考坐标[5-6]。两种姿态角从不同的角度描述了飞行器相对参考坐标系的姿态关系,姿态角通常以姿态矩阵的形式表现。

2.1 共用坐标系

1)地心惯性坐标系(简称:i系):用oxiyizi表示,原点为地球中心,xi、yi轴在地球赤道平面内,xi轴指向春分点,zi轴为地球自转轴。

2)地球固连坐标系(简称:e系):用oxeyeze表示,原点为地球中心,xe、ye轴在地球赤道平面内,xe指向本初子午线,ze轴为地球自转轴。

2.2 航天领域坐标系

1)发射坐标系(简称:发射系,g系):坐标原点与发射点o固连,ox轴在发射点水平面内,指向发射瞄准方向,oy轴垂直于发射点水平面指向上方,oz轴与xoy面相垂直并构成右手直角坐标系。

2)发射惯性系(简称:发惯系,a系):飞行器起飞瞬间,坐标原点oa与发射点o重合,各坐标轴与发射坐标系各轴也相应重合。飞行器起飞后,oa点及坐标系各轴方向在惯性空间保持不动。发射惯性系为航天飞行器导航参考坐标系。

3)弹体坐标系(简称:ba系):坐标原点o为飞行器的质心,oxba轴为飞行器外壳对称轴,指向头部,oyba轴在飞行器的主对称面内,oyba轴垂直于oxba轴,向上为正,ozba轴与xbaoyba面相垂直并构成右手直角坐标系。

弹体坐标系(ba系)相对于发惯系(a系)的姿态角为航天制导导航和六自由度模型使用的姿态角,分别用φa、ψa和γa表示。姿态矩阵如下所示。

(8)

其中,c为cos,s为sin。

2.3 航空领域坐标系

1)导航坐标系(简称:n系):原点为飞行器中心,xn轴指向东,yn轴指向北,zn轴指向天,n系为当地水平坐标系。

2)弹体坐标系(简称:bn系):原点为飞行器的质心,xbn轴沿飞行器横轴向右,ybn轴沿飞行器纵轴向前,zbn轴沿飞行器立轴向上。

弹体坐标系(bn系)相对于导航坐标系(n系)的姿态角为当地水平捷联算法使用的姿态角,分别用ψn、θn和γn表示。姿态矩阵如下式所示。

(9)

2.4 坐标系关系分析

以上的各坐标系可用图5表示,各坐标系之间的姿态矩阵可用图6表示。

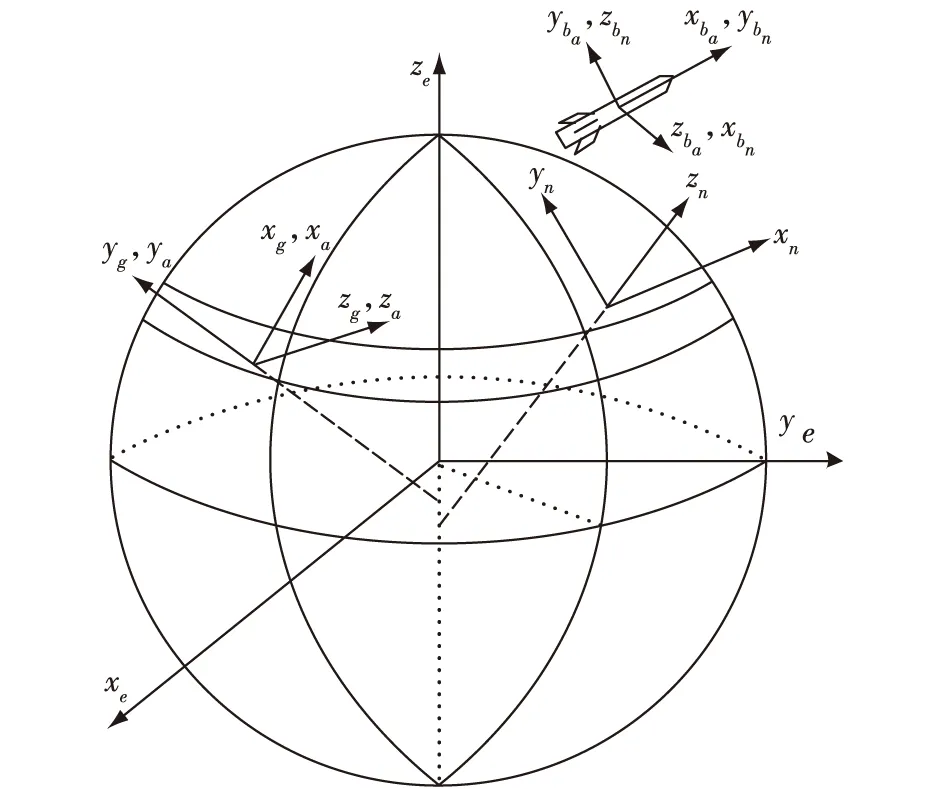
图5 坐标系关系

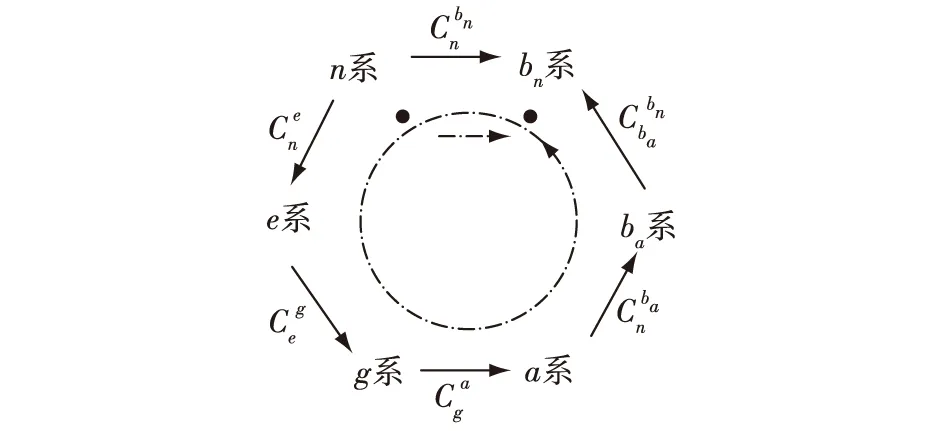
图6 姿态矩阵传递关系

2.5 姿态矩阵关系分析

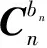
(10)

各姿态矩阵的定义为:

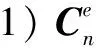
(11)

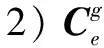
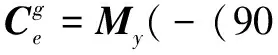
(12)

(13)

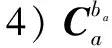
3 半实物仿真验证

为了说明和验证姿态角转换关系,在某高超声速助推-滑翔飞行器半实物仿真系统(如图1所示)中,进行了仿真验证。在其半实物仿真中,发射的初始条件:初始经度λ0=33°、纬度φ0=0°和航向α0=0°。为了比较姿态的转换关系,半实物仿真六自由度模型中发射惯性系只有俯仰角运动,如图7所示,偏航角和滚转角为0°。

如图8所示,当飞行器平飞阶段,当地水平坐标系下俯仰角维持在0°附近。虽然半实物仿真六自由度模型中,未设置滚转和偏航角机动,由于地球曲率的影响,当地水平坐标系下的滚转角和航向角均有显著变化,如图9和图10所示;在约73s前,由于俯仰角在90°附近,当地东北天坐标系下滚转角和航向角出现奇异,属正常现象。通过坐标转换理论,本文通过16次坐标转换,将发射点惯性坐标系下的姿态矩阵/姿态角转换到当地水平系的姿态矩阵/姿态角。半实物仿真中的卫星模拟器和图像模拟器均需要当地水平系的姿态角信息。

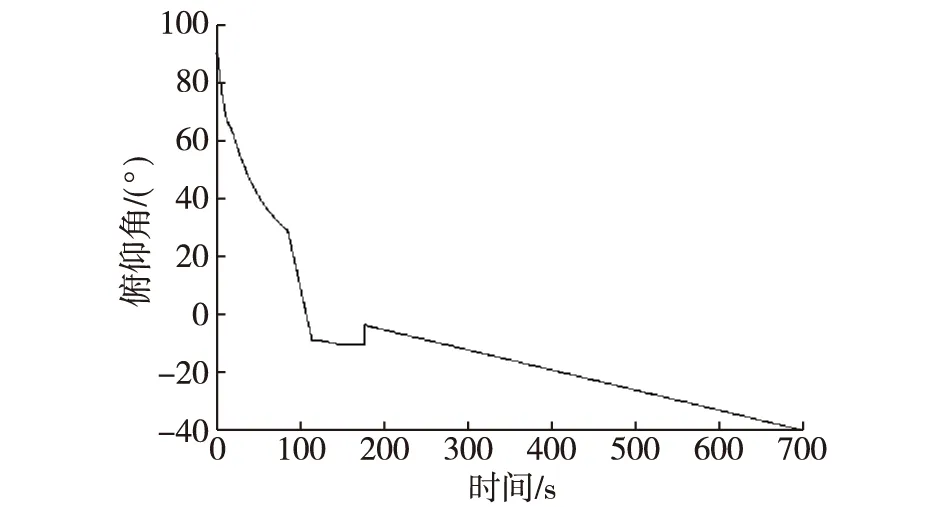
图7 发射点惯性坐标系下俯仰角

图8 当地水平坐标系下俯仰角

图9 当地水平坐标系下滚转角

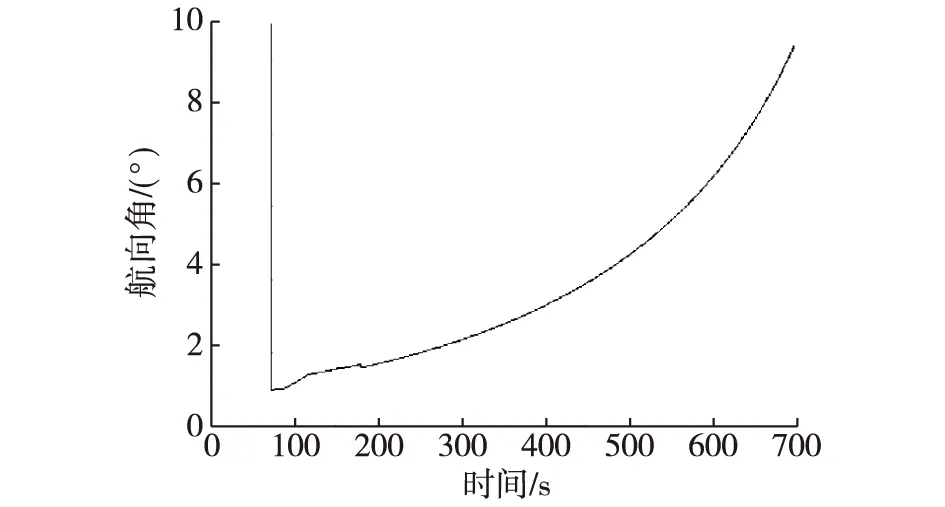
图10 当地水平坐标系下航向角

4 结束语

本文介绍了坐标转换理论,逐步推导出临近空间飞行器半实物仿真中两种姿态矩阵的理论关系,并进行了半实物仿真验证。该方法保证了半实物仿真中导航试验的顺利实施。坐标转换理论也可应用到导航坐标系之间的姿态矩阵转换。

[1] 闫杰,于云峰,凡永华,等. 吸气式高超声速飞行器控制技术[M].西安：西北工业大学出版社,2015.

[2] Curtis Peebles. Road to Mach 10: Lessons Learned from the X-43A Flight Research Program[M].AIAA,2008

[3] Chang X F, Yang T, Yan J, et al. Design and integration of hardware-in-the-loop simulation system for certain missile[C]∥ICSC 2012, Springer Verlag, 229-237.

[4] 张卫东.运载火箭动力学与控制[M]. 北京：中国宇航出版社, 2015.

[5] 陈凯, 卫凤, 张前程，等. 基于飞行力学的惯导轨迹发生器及其在半实物仿真中的应用[J]. 中国惯性技术学报, 2014, 22(4):486-491.

[6] 秦永元. 惯性导航[M]. 北京：科学出版社, 2014.

[7] 刘敏. 坐标转换在组合导航系统半实物仿真中的应用[J]. 计算机仿真,2005,22(10):136-139.

[8] 袁智荣. 火箭弹制导化中的坐标转换问题[J]. 测控技术,2009,28(11):91-94.

[9] 吴盘龙,姜福先. 精确制导炸弹坐标转换技术[J]. 中国惯性技术学报,2008,11(2):174-177.

[10]秦玉亮,李宏,王宏强,等. 基于SAR导引头的弹体定位技术[J]. 系统工程与电子技术,2009,31(1):121-124.

[11]Zhao H T, Zhang B, Wu C S, et al. Development of a Coordinate Transformation method for direct georeferencing in map projection frames[J].ISPRS Journal of Photogrammetry and Remote Sensing,2013,77:94-103.

[12]Shuster, M. A Survey of Attitude Representations[J].Journal of the Astronautical Sciences, 1993, 41(4):439-517.

[13]W. F. Phillips, C. E. Hailey, G. A. Gebert. Review of Attitude Representations Used for Aircraft Kinematics[J].Journal of Aircraft, 2001,38(4): 718-737.

Coordinate Transformation with Application in HWIL Simulation

CHEN Kai, WANG Xiang, LIU Ming-xin, YU Yun-feng, YAN Jie

(School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The relationship between the direction cosine matrix (DCM) in the space field and DCM in the aeronautics field is derived, to meet the demand of hardware-in-the-loop (HWIL) simulation of near space hypersonic vehicle flight control system. Firstly, the coordinate transformation (CT) theory is introduced, and the conversion method between two cartesian coordinate system is Introctuced. As well as the relationship of DCMs between the matrix transformation under two different reference systems is presented. Then, the analyzes the relationship of coordinate frames between the space field and the aeronautics field. How to convert the coordinate frame in the space field to the coordinate frame in the aeronautics field is researched. Finally, the HWIL simulation indicates that the method is correct and feasible. It ensures the HWIL simulation of navigation system of near space hypersonic vehicle.

Coordinate transformation; direction cosine matrix (DCM); Hardware-in-the-loop (HWIL) simulation; strapdown inertial navigation; Near space hypersonic vehicle

2016-09-29

2016-11-06

国家安全重大基础研究项目(973)；航天科技创新基金；卫星导航系统与装备技术国家重点实验室基金。

陈 凯(1976-)，男，江苏连云港人，博士，副教授，研究方向为惯性导航、飞行器仿真。 王 翔(1992-),男，硕士研究生。 刘明鑫(1994-),男，本科。 于云峰(1966-),男，教授。 闫 杰(1961-)，男，教授。

1673-3819(2017)02-0118-05

V249.3；E917

A

10.3969/j.issn.1673-3819.2017.02.022