基于反导探测能力的舰队队形优化分析方法
2017-05-11朱燕麒伍国华祝江汉
朱燕麒,刘 进,伍国华,祝江汉
(国防科学技术大学信息系统与管理学院,湖南 长沙 410073)
基于反导探测能力的舰队队形优化分析方法
朱燕麒,刘 进,伍国华,祝江汉
(国防科学技术大学信息系统与管理学院,湖南 长沙 410073)
在已有的技术条件下,为提高舰队对来袭导弹的探测性能,对舰队队形进行优化。为克服传统队形优化方法难以充分考虑不同舰船探测性能的差异且无法给出舰队中各舰最优相对位置坐标的缺陷,利用各舰探测概率-距离实验数据拟合函数,采用蒙特卡罗方法模拟导弹被探测坐标点,在三个区域建立舰队反导探测能力函数。以此函数为优化目标,并根据实际队形要求建立约束条件,得到基于反导探测能力的舰队队形优化模型。应用差分进化算法求解约束优化问题,解出最优队形下各舰位置坐标。模型测试结果表明,该方法能有效提升舰队反导探测性能,给出合理的队形优化方案。
反导;队形优化;蒙特卡罗方法;差分进化
在目前技术条件下,空中力量尤其是各类反舰导弹对于水面舰艇的安全产生了巨大威胁,水面舰艇编队的防空能力成为衡量其生存能力的重要指标。要使水面舰艇最大程度地免受空中力量的打击,就要做到早发现、早拦截、早摧毁,对于空中目标尤其是反舰导弹的探测能力是至关重要的前提,决定了拦截和打击的反应时间。目前,各类反舰导弹为提高生存能力及突防能力,多采用超低空掠海飞行方式,这使得舰载雷达的探测预警距离被大大压缩,甚至只有20km。
舰艇编队中各水面舰艇之间的距离是影响探测预警范围的重要因素,选择适当的防空舰艇编队队形,对最大限度提高编队的整体对空防御能力具有重要意义[1],本文将对其进行分析与优化。
李浩、王公宝分析了典型防空队形如菱形、人字形、梯形等,建立了编队防空队形综合评判的指标体系,并应用模糊层次分析法建立了编队防空队形优选模型,初步解决了编队防空队形优选问题[2]。
李微波等针对队形变化给编队防空能力带来的五个方面的影响,建立了基于模糊综合评判的防空队形评估模型,对科学评估舰队防空能力具有积极意义[3]。目前基于反导探测能力进行舰队队形优化的研究,主要是对一些经典的防空队形建立指标体系,通过层次分析等方法建立评估模型对不同队形下的舰队防空性能进行评估对比,得到指导性的舰队队形设置原则[4]。这一类方法在实际应用中存在以下两个问题:一是在逻辑上是基于给定的若干队形方案,在对其进行评估的基础上进行优化,不具备根据实际态势主动生成最优方案的功能;二是在优化时难以考虑不同舰船对空探测性能的差异,认为各舰具备相同的对空探测能力。对于作战效能的评估问题,蒙特卡罗随机仿真实验具有很好的效果[5]。基于以上分析,本文将利用各舰探测概率-距离实验数据拟合函数,采用蒙特卡罗方法模拟导弹被探测坐标点,在三个区域综合建立舰队反导探测能力函数。以此函数为优化目标,并根据实际队形约束建立约束条件,得到基于反导探测能力的舰队队形优化模型。应用差分进化算法求解约束优化问题,解出最优队形下各舰位置坐标,得到确定编队各舰位置的通用方法,为灵活高效构建合理的舰队队形提供方法指导。
1 问题背景
某一作战海域有我方水面舰艇编队执行作战任务,编队由一艘指挥舰,n艘作战舰艇组成。现已知敌方空中威胁可能来源方位、舰载雷达探测性能等信息,需对编队的队形进行优化设计,实现在作战海域对于敌方空中威胁的最佳探测能力,从而保证编队指挥舰的安全,为作战指挥部门提供决策依据。
2 基于反导探测能力的舰队队形优化分析模型
2.1 模型假设与说明
基于反导探测能力的舰队队形优化分析模型基于如下假设:
1)由于通过蒙特卡罗方法仿真的是导弹被舰队探测到时的坐标位置,为瞬时的状态值,因此无需考虑舰队本身的航行速度。
2)在航行过程中,舰队队形基本保持不变。
3)对于探测能力的描述基于编队首次发现来袭空中目标的性能,不考虑探测后目标丢失的情况。
4.编队各舰具有完备的通信链路,当编队中一艘舰艇发现目标,即认为舰艇编队实现对目标的成功探测。
5)不考虑不同舰艇探测设备之间的相互干扰。
基于反导探测能力的舰队队形优化分析模型的几点说明:
1)在其它因素不变条件下,已知指挥舰与各作战舰艇的反导防空探测概率-距离函数
p(s),p1(s),p2(s)…pn(s)
表示该舰在距离s上探测到来袭目标的概率,称为反导防空探测性能函数。
2)通过卫星、无人机或地面雷达等侦察手段已知作战海域敌方导弹威胁情况。例如,以我指挥舰为原点的20°至220°扇面内可能有导弹来袭。
3)指挥舰指挥中心为己方体系关键节点,反导探测能力主要面向对指挥舰的保护。
4)舰队队形编成的约束条件包括任意两舰之间的最小安全距离以及任意两舰之间的最大距离。
2.2 基于反导探测能力的舰队队形优化分析模型构建
2.2.1 目标准则
本文认为,一个比较好的舰船编队,在搜索探测性能上应该满足“在尽可能远的距离上,以尽可能大的概率发现来袭目标”。这个要求中有两个变量:距离和概率,而且这是一个模糊问题,比较难求解。下面将这个要求具体化为以下3个指标:
舰队在距指挥舰较远的距离上对来袭目标的发现概率,记为F1;
舰队在距指挥舰适中的距离上对来袭目标的发现概率,记为F2;
舰队在距指挥舰较近的距离上对来袭目标的发现概率,记为F3。
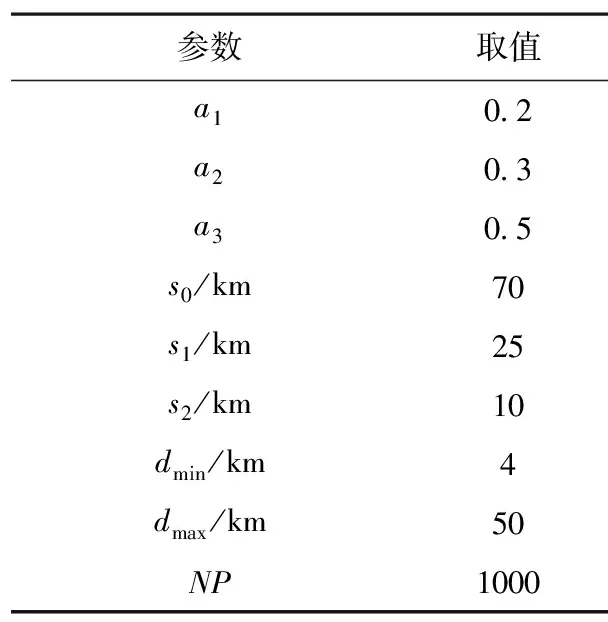
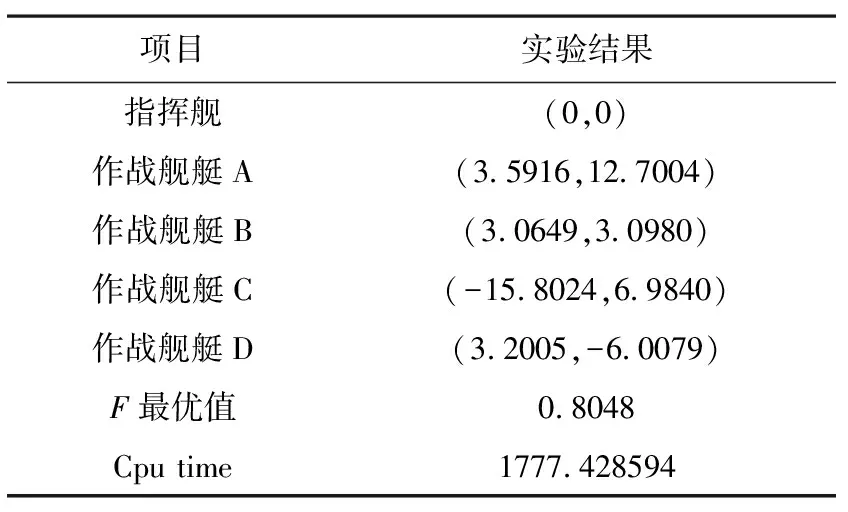
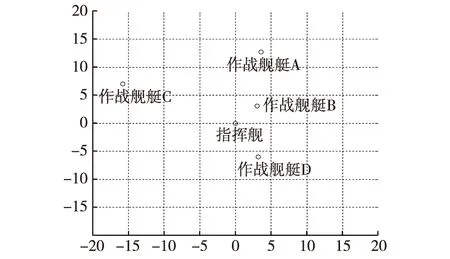
在实际作战过程中,一般认为F1 F=a1F1+a2F2+a3F3,a1+a2+a3=1。 2.2.2 目标函数建立 由目标准则的分析可知,对舰队队形优化的目的是使F的值达到最大,在已知指挥舰与各作战舰艇的反导防空探测性能函数以及作战海域敌方导弹威胁情况的前提下,需要通过仿真实验的方法确定F的表达式,具体分析如下: 对于舰队防空,3km属于反导探测的临界距离,因此将较近距离范围的下限设置为3km。 根据具体任务情况,确定任务中“较远的距离范围”Ω1∈[s1,s0),“适中的距离范围”Ω2∈[s2,s1)以及“较近的距离范围”Ω3∈[3,s2)的具体取值。然后以指挥舰指挥中心为坐标原点建立平面直角坐标系,将n艘作战舰艇的位置表示为(x1,y1),(x2,y2),…,(xn,yn),将首次发现来袭导弹的位置坐标表示为(x,y)。对于确定了的距离范围,根据作战海域敌方导弹威胁情况,在三个区域Ω1、Ω2和Ω3分别模拟产生NP个坐标点(xj,yj)其中j=1,2,…,NP,即 从而作战舰艇i对某一导弹在模拟点(xj,yj)的发现概率为: (1) 根据概率公式,整个舰队对某一导弹在区域Ωk模拟点(xj,yj)的发现概率为: (2) (3) 根据目标准则确定a1,a2和a3的取值,将目标函数F确定为: F=a1F1+a2F2+a3F3,a1+a2+a3=1 (4) 这样,F是关于x1,y1,x2,y2,…,xn,yn的2n维函数。 2.2.3 约束条件建立 设任意两舰之间的最小安全距离为dmin,任意两舰之间的最大距离为dmax。则有 (5) (6) (7) (8) 其中式(5)、(6)表示作战舰艇i与指挥舰之间的距离约束,式(7)、(8)表示作战舰艇之间的距离约束。 2.2.4 基于反导探测能力的舰队队形优化分析模型 综合以上分析,得到基于反导探测能力的舰队队形优化分析模型如下所示: 由于F是关于x1,y1,x2,y2,…,xn,yn的2n维函数,当n较大时,属于高维优化问题。并且对于不同的距离范围,模拟导弹的数量NP较大,且指挥舰与各作战舰艇的反导防空探测性能函数p(s),p1(s),p2(s),…,pn(s)一般是由测试实验数据拟合而来,其表达形式可能较为复杂。因此,计算的复杂度高,考虑计算时间的要求,难以使用解析算法进行精确求解,考虑采用启发式算法对其进行求解计算。 3.1 差分进化算法简介 差分进化算法(Differential Evolution)是一种新兴的进化计算技术。其是由Storn等人于1995年提出的,和其他演化算法一样,DE是一种模拟生物进化的随机模型,通过反复迭代,使得那些适应环境的个体被保存了下来。但相比于进化算法,DE保留了基于种群的全局搜索策略,采用实数编码、基于差分的简单变异操作和一对一的竞争生存策略,降低了遗传操作的复杂性。同时,DE特有的记忆能力使其可以动态跟踪当前的搜索情况,以调整其搜索策略,具有较强的全局收敛能力和鲁棒性,且不需要借助问题的特征信息,适于求解一些利用常规的数学规划方法所无法求解的复杂环境中的优化问题。目前,DE已经在许多领域得到了应用,譬如人工神经元网络、化工、电力、机械设计、机器人、信号处理、生物信息、经济学、现代农业、食品安全、环境保护和运筹学等。 DE算法主要用于求解连续变量的全局优化问题,其主要工作步骤与其他进化算法基本一致,主要包括变异(Mutation)、交叉(Crossover)、选择(Selection)三种操作[6]。算法的基本思想是从某一随机产生的初始群体开始,利用从种群中随机选取的两个个体的差向量作为第三个个体的随机变化源,将差向量加权后按照一定的规则与第三个个体求和而产生变异个体,该操作称为变异。然后,变异个体与某个预先决定的目标个体进行参数混合,生成试验个体,这一过程称之为交叉。如果试验个体的适应度值优于目标个体的适应度值,则在下一代中试验个体取代目标个体,否则目标个体仍保存下来,该操作称为选择。在每一代的进化过程中,每一个体矢量作为目标个体一次,算法通过不断地迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程向全局最优解逼近。 其过程具体表达为: 1) mutation:对于每个目标向量 xi,G,i=1,2,3,…,N 交叉向量为 vi,G+1=xr1,G+F·(xr2,G-xr3,G) 其中r1,r2,r3∈{1,2,…,N}随机产生,F为常数,N为种群规模。 2)crossover:试验向量的形式为 ui,G+1=(u1i,G+1,u2i,G+1,…,uDi,G+1) D为问题维数,构造试验向量的规则为 其中j=1,2,3,…,D,CR为常数。 3)selection:基于贪心法则进行选择。 3.2 求解思路 现对模型求解思路进行简要介绍。 1)根据任务情况,通过AHP等分析方法得出a1,a2和a3的值,并分析确定s0,s1和s2以及dmin,dmax和NP的取值。 2)根据情报获知作战海域的敌方导弹威胁情况,若无有效情报则视为等可能分布。利用s0,s1和s2以及NP的取值,分别在不同距离范围上模拟产生NP数量的导弹发现点。 3)利用仿真出的导弹发现点以及指挥舰与各作战舰艇的反导防空探测性能函数p(s),p1(s),p2(s)…pn(s)表示舰队在对于某一导弹在模拟点被发现的概率: 其中 模拟导弹被探测时的坐标满足: 优化目标函数为: F=a1F1+a2F2+a3F3,a1+a2+a3=1 F是关于x1,y1,x2,y2,…,xn,yn的2n维函数。 4)根据舰队队形编成的约束条件,利用差分进化算法进行有约束的搜索,得到最优坐标值,即可得出最优队形。 4.1 测试数据 某一作战海域有我方水面舰艇编队执行作战任务,编队由一艘指挥舰,4艘作战舰艇组成。现已知敌方空中在以指挥舰为原点的全作战海域等可能来袭。己方体系关键节点为指挥舰的作战指挥中心。在舰队编成时,要求任意两舰之间的最小距离不得少于4km,任意两舰之间的最大距离不得大于50km。 各舰防空探测性能函数如表1所示。 表1 各舰防空探测性能函数 4.2 模型求解过程 1)基于任务及情报信息,在此案例下设置参数如表2所示。 表2 案例参数设置 2)作战海域敌方导弹威胁情况显示以指挥舰为原点360°方向等可能来袭,在3个不同区域分别依此分布模拟1000个来袭导弹被首次探测到时的坐标位置。 3)利用仿真模拟出的3组1000个来袭导弹被首次探测到时的坐标位置给出目标函数F。 4)利用差分进化算法对目标函数进行有约束搜索。经过多次预实验分析,当F取0.5,CR取0.9时搜索效果较好。差分进化算法中,一般将种群规模N设置为问题维数的3~5倍[7],此例为8维优化问题,将种群规模设置为40。在预实验中,发现该问题利用差分进化算法优化过程中收敛速度很快,在100代左右即实现了很好的收敛效果。因此迭代次数不必设置过大,本文将其设置为500。差分进化算法各参数设置如表3所示。 表3 差分进化算法参数设置 4.3 实验结果 利用Matlab进行实验,求解结果如表4所示。 表4 实验结果 各代最优解进化过程如图1所示。 图1 优化过程示意 图中,横轴代表差分进化算法的迭代次数,纵轴代表各代种群中目标函数的最优值。可见对于该问题,差分进化算法收敛速度很快,且最终优化结果0.8048对于初代种群最优值0.6080有较大提升,100代以后目标函数在0.80附近小幅震荡,实现了较好的收敛效果。舰队队形示意如图2所示。 图2 舰队队形示意图 由示意图可知,该最优方案类似于人字舰队队形,舰队主体呈类似纵队队形,根据各舰船坐标值进行检验计算,验证该方案符合实际情况和约束条件。充分考虑了不同舰船反导探测性能的差异,可以与传统队形设计方案结合使用,为舰队队形的最优设计提供方法借鉴。 4.4 对比分析 为直观对比该优化分析方法的有效性,现将优化队形方案与传统常见舰队队形方案进行简单比较。舰队编队常见队形主要有菱形、梯形、横队、纵队和环形等,对比结果如表5所示。 表5 其他队形方案表现 由目标函数值的简单对比可知,优化方案与未加优化的传统队形方案相比,在F的取值上提升了8.713%~20.986%。 在传统常见舰队队形中,纵队队形的性能最为优异,在案例所设导弹威胁情况下表现出较好的反导探测能力,优化程度较高。而本方法得到的最优方案在主体上基本也呈现纵队队形,从而进一步验证了模型的合理性和科学性。由于模型充分考虑了不同作战舰艇在反导探测性能上的差异,因此比标准的纵队队形优化程度更高。 对比分析的结果表明,本方法的模型具备科学性和合理性,能够在充分考虑不同作战舰艇在反导探测性能差异的基础上自动生成最优队形方案,可以为传统的队形设计方法提供优化指导。 1)基于反导探测能力的舰队队形优化模型和基于蒙特卡罗的差分进化寻优算法能够准确快速地给出舰队中各舰的坐标位置,从而给出优化的备选方案。 2)基于反导探测能力的舰队队形优化模型考虑了不同舰船反导探测性能的差异,具有一定的适用性,可以与传统队形设计方案结合使用,为舰队队形优化提供参考。 3)本文的队形优化主要是基于反导探测性能,在后续的研究中,应全面考虑队形编成所涉及的其他约束条件和优化目标,进一步优化该分析方法,提高其普适性。 [1] 赵畅.水面舰艇编队队形模型构建探讨[J]. 廊坊师范学院学报(自然科学版), 2015, 15(6):9-12. [2] 李浩,王公宝.关于水面舰艇编队防空队形的优化研究[J]. 舰船科学技术, 2009, 31(5):109-112. [3] 李微波,傅调平,鄢力,等.基于模糊综合评判的舰艇编队防空队形优化研究[J]. 舰船电子工程, 2012, 32(4):25-27. [4] 姜鲁东,孙建华,余家祥.舰艇护航编队防空队形配置方法研究[J]. 舰船电子工程, 2014, 34(2):19-21. [5] 李涛,柳林,吴小勇.基于蒙特卡洛仿真的驱护编队防空队形配置研究[J]. 舰船电子工程, 2014, 34(3):33-36. [6] Storn R, Price K. DE-a simple and efficient heuristic for global optimization over continuous space[J]. Journal of Global Optimization, 1997, 114(4):341-359. [7] Brest J, Greiner S, Boskovic B, et al. Self-Adapting Control Parameters in Differential Evolution: A Comparative Study on Numerical Benchmark Problems[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6):646-657. Fleet Formation Optimization Analysis Method Based on Anti-missile Detection Ability ZHU Yan-qi, LIU Jin, Wu Guo-hua, ZHU Jiang-han (College of Information System and Management, National University of Defense Technology, Changsha 410073, China) Under the existing technical conditions, optimize the fleet formation to improve the detection performance of the fleet against missiles. To overcome shortcomings of traditional formation evaluation and optimization methods which are difficult to give full consideration to the differences of the detection performance of different ships and to give the relative position coordinates, use detection performance functions from the experimental data and Monte Carlo simulation missiles to establish optimization function. Establish the optimal objective function based on this function and establish the constraint condition according to the actual formation constraints. Then obtain the optimization model of the fleet formation based on the anti-missile detection capability. Using Differential Evolution, optimize this function by constrained search to determine the coordinates of ships. Test results show that the method can effectively improve the detection performance of the fleet, and give a reasonable formation optimization scheme. anti-missile; formation optimization; Monte Carlo simulation; Differential Evolution 2016-09-22 2016-12-16 自然科学基金(61603404);国防科技大学科研计划项目(zk16-03-30) 朱燕麒(1992-),男,河南新乡人,硕士研究生,研究方向为演化计算、模糊决策。 刘 进(1982-),男,讲师,博士。 伍国华(1986-),男,讲师,博士。 祝江汉(1972-),男,教授,博士。 1673-3819(2017)02-0036-05 TJ762.3+3;E917 A 10.3969/j.issn.1673-3819.2017.02.008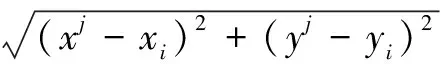

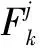
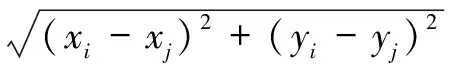
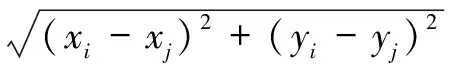

3 模型求解方法

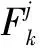
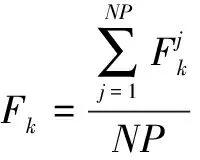
4 模型测试与应用




5 结束语
