蓝宝石表面形貌的功率谱与分形特征分析

许永超, 陆 静* , 徐西鹏

(1.华侨大学 制造工程研究院，福建 厦门 361021;2.华侨大学 脆性材料加工技术教育部工程研究中心，福建 厦门 361021)

蓝宝石表面形貌的功率谱与分形特征分析

许永超1,2, 陆 静1,2*, 徐西鹏1,2

(1.华侨大学 制造工程研究院，福建 厦门 361021;2.华侨大学 脆性材料加工技术教育部工程研究中心，福建 厦门 361021)

运用二维功率谱和分形理论的关联维数分析了蓝宝石晶片的表面形貌特征。介绍了利用二维快速傅立叶变换计算二维功率谱在蓝宝石表面形貌中的应用方法；通过时间延迟技术重构相空间，利用G-P算法计算了蓝宝石表面形貌的关联维数。分别利用二维功率谱和关联维数对蓝宝石的原始表面、加工后表面和单个取样长度的形貌特征进行了实验分析。结果表明：二维功率谱和关联维数能够表征蓝宝石表面形貌，且克服了传统的表征参数只包含有垂直方向上的信息而不能准确表征整个蓝宝石晶片表面形貌特征的缺点，它比传统的表面形貌表征方法具有准确、便捷和信息量大等优势。

蓝宝石;二维功率谱;关联维数;表面形貌

1 引 言

蓝宝石因具有良好的热特性、极好的电气特性和介电特性而被广泛应用于制造GaN基发光二极管LED的衬底片材料[1-3]。随着光电子技术和光通讯技术的发展，对蓝宝石晶片的加工质量有着非常高的要求。表面形貌历来就作为评价蓝宝石晶片加工质量的一项重要指标[4]。

目前关于表面粗糙度的国家标准主要是针对二维轮廓进行评定的，提出了三类评定表面粗糙度的参数，其中包括用于描述表面轮廓高度的统计特性、极值特性和分布特性的幅值参数，描述表面峰值间距特性的空间参数和用来综合反映表面轮廓形状特性的综合参数[5-6]。各种不同的测量技术和测量仪器的使用使超精密加工后蓝宝石晶片的表面质量和粗糙度的测试和评价变得更加便利，但这些仪器所测得的粗糙度等参数仅是通过一些简单的统计数据来描述的，如平均粗糙度、PV值和均方根值粗糙度等。这些表征参数只包含有垂直方向上的信息，忽略了很重要的横向和纵向空间信息的分布情况，因此不能准确表征整个蓝宝石晶片的表面形貌特征[7-8]。如何对整个蓝宝石表面形貌进行准确描述已成为一项重大课题。

蓝宝石表面形貌信号的空间波形是极不光滑的，其变化趋势没有一个确定的函数关系，但这些非线性特征信号在一定的尺度范围内都具有随机性和混沌特征。随着以随机过程理论为基础的表面形貌识别技术和非线性动力学中混沌时间序列信号的相空间重构理论研究的不断深入，时序模型的功率谱已发展为轮廓与表面的功率谱，它可以更确切地描述表面形貌的各项特征，而混沌理论中的分形维数是定量描述混沌吸引子的一个重要参数，被广泛应用于定量描述系统的非线性行为[9]。本文将通过功率谱和分形理论来分析蓝宝石的表面形貌特征，探讨表征蓝宝石表面形貌特征的新方法。

2 功率谱和分形维数算法

2.1 功率谱法

表面谱分析是时域或空域信息转换到频率域的强有力工具[10]，其将表面轮廓波形分解为不同正弦表面的叠加，能够突出单个频率或空间波长的信息，还可以反映出不同空间波长成分在整个信息中所占的比重，从而相对地揭示出不同空间波长成分对表面粗糙度的影响。经过超精密加工的光滑表面在微观程度上都表现为三维的高低起伏，表面粗糙度就是对这种表面上的微峰谷在Z方向上进行的统计描述z(x，y)。若，以栅格扫描方式对单晶蓝宝石片在x，y方向上按Nyquist准则选择采样步距，分别以固定间隔Tx、Ty，采样点数分别为M和N进行采样，则函数z(x，y)变为z(pTx，qTy)，其中p=0,1,2,……,M-1；q=0,1,2,……,N-1。则其对应的离散二维FFT为

(1)

式中，u=0，1，2，……，M-1；v=0，1，2，……，N-1。fu=u/(MTx)，fv=v/(NTy)。采用最有效和广泛使用的周期图法来估计其相应的离散功率谱密度可近似表示为

当用这种周期图法作谱估计时，存在着功率谱密度的统计变异和能量泄漏两个问题，前者为统计误差，是由于采集数据数量有限而引起的不确定度；后者是谱分析中的固有问题，其会引起谱估计的偏度误差，因此在实际处理技术上往往需要对周期图法进行修改以尽量减小误差。如对测量数据进行分段平滑处理，以减小统计变异性，以及采用数据窗处理以减小泄漏等[10]。

2.2 分形法

经研磨后的蓝宝石表面结构具有很强的自相似性。将分形维数应用于介观尺度下蓝宝石表面特征的研究，为研究蓝宝石复杂表面特征提供了一种新的思路和方法。由Takens重构定理可知，一个动力系统在演化过程中其各个变量之间存在内在的联系，系统中任一变量的演化都是与系统其他变量相互作用所决定的，任一变量的演化过程中也就隐含了系统的演化信息[11]。分形维数是定量描述分形特征的主要参数。表面分形维数越大，表面结构越复杂。在众多的分形维数中，关联维数由于对吸引子的不均匀性反应敏感，更能反映吸引子的动态结构，且关联维数易于从实验数据中直接测定，求解关联维数的G-P算法简单可靠，所以关联维数常被用来描述时间序列的分析特征。根据此重构定理，采用时间延迟技术重构相空间。相空间重构后选择关联维数作为系统状态空间吸引子的分维数，根据Grassberg和Procaccia提出的用于计算关联维数的G-P算法[12]，关联积分C(r)可表示为

(3)

式中，L为重构后向空间矢量个数；r为重构相空间的标度。

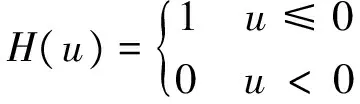
(4)

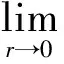
(5)

一般情况下，常作出关联积分C(r)与标度r的双对数曲线，即关联积分曲线。把曲线中一段近似直线范围所对应的标度范围作为标度区，再通过最小二乘法拟合出对应的直线，该直线的斜率即为所求的关联维数。

其中，计算过程中所需确定的延迟时间τ取其自相关函数值首次出现零点时的时延为所需确定的时间延迟；利用系统特征饱和法，嵌入维数m取其关联维数达到饱和时所对应的嵌入维数。

3 实验分析

现选用未经过抛光的原始表面和经过金刚石磨粒抛光后的蓝宝石晶片表面进行具体分析。通过三维表面轮廓测量ZYGO测量仪对两蓝宝石晶片的表面形貌进行观察。蓝宝石原始表面两个不同部位测得的表面形貌如图1所示。经金刚石磨粒抛光后的蓝宝石晶片不同部位的表面形貌如图2所示。

图2 经过金刚石磨粒抛光后蓝宝石晶片不同部位的表面Fig.2 Surfaces of different parts of the sapphire wafer after polishing by diamond abrasives

由图1可知，对于加工精度要求要达到纳米级的蓝宝石晶片而言，同一个晶片表面上不同部位的轮廓最大高度相差0.446μm已是一个非常大的差异，但实际中经常用来评价表面质量的Ra值在这两个不同部位的数值却同为0.086nm。在图2中，金刚石磨粒在不同部位留下的加工痕迹差别也是比较大的，但这两个部位的Ra值却同为0.006nm。由此可知，传统的表面形貌表征方法不能全面反映表面信息，甚至有时会给出错误的反映。

现分别用二维功率谱法和分形法分析这两个不同蓝宝石晶片的表面特征。

根据上文2.1的内容得出蓝宝石原始表面和加工后表面的二维功率谱图如图3和图4所示。

由图3和图4可知，不同的蓝宝石表面形貌所对应的功率谱分布存在着很大差异。在分布图边缘上功率谱分布为零，说明蓝宝石的表面形貌是非线性的。分四段计算两表面结构分别对应的关联维数分别为0.0322、0.0335、0.0374、0.0299和-2.8433e-19、0.0045、4.1912e-8、-2.2747e-19。蓝宝石经抛光后的表面结构发生很大变化，表面微峰大量减少，更趋于平整。对应于二维功率谱中，任意两正交频率对应的功率谱波峰分布也更为均匀；关联维数也更小，趋向于零。

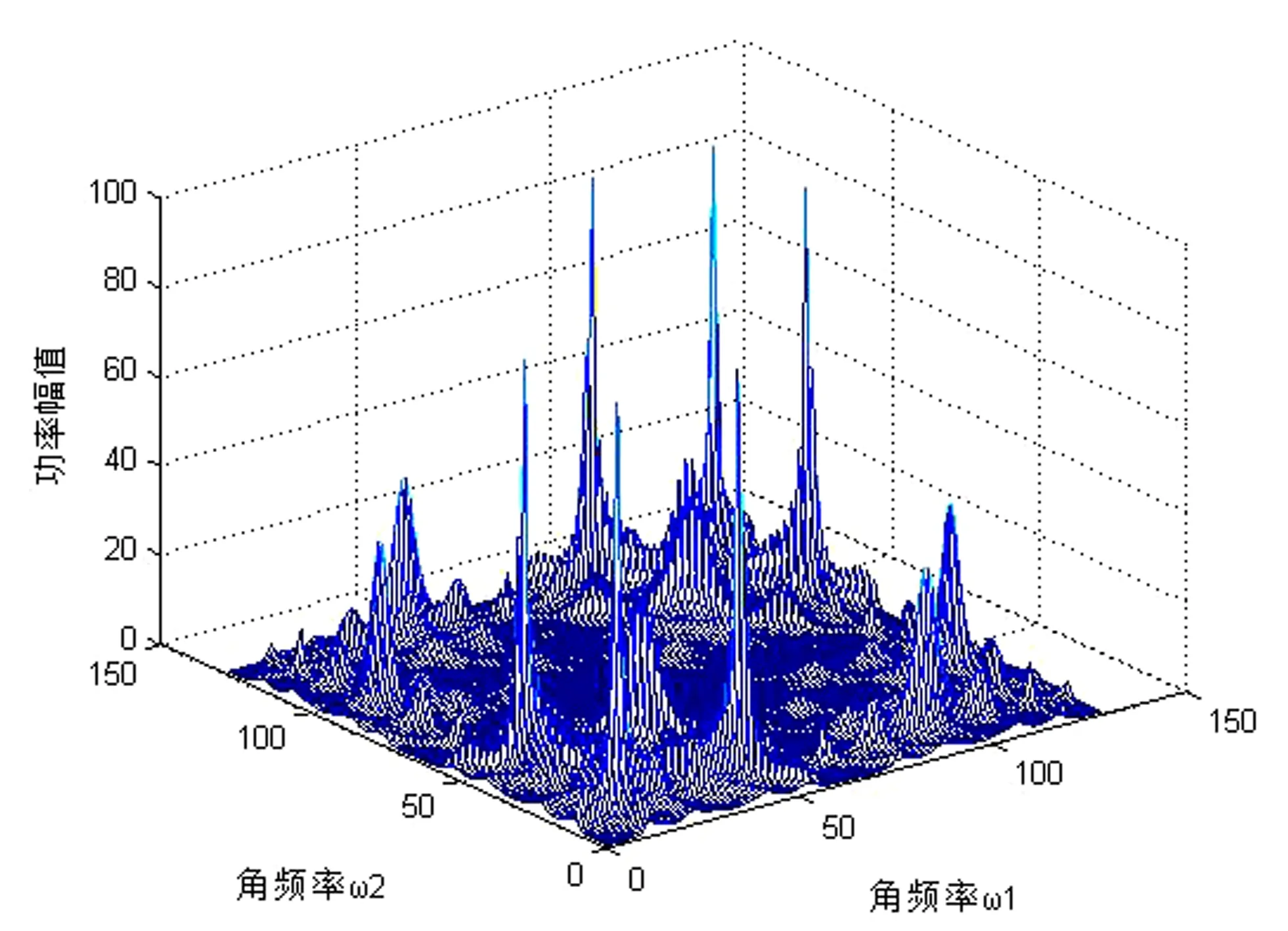
图3 蓝宝石原始表面的二维功率谱图Fig.3 2D power spectrum of original surface of sapphire

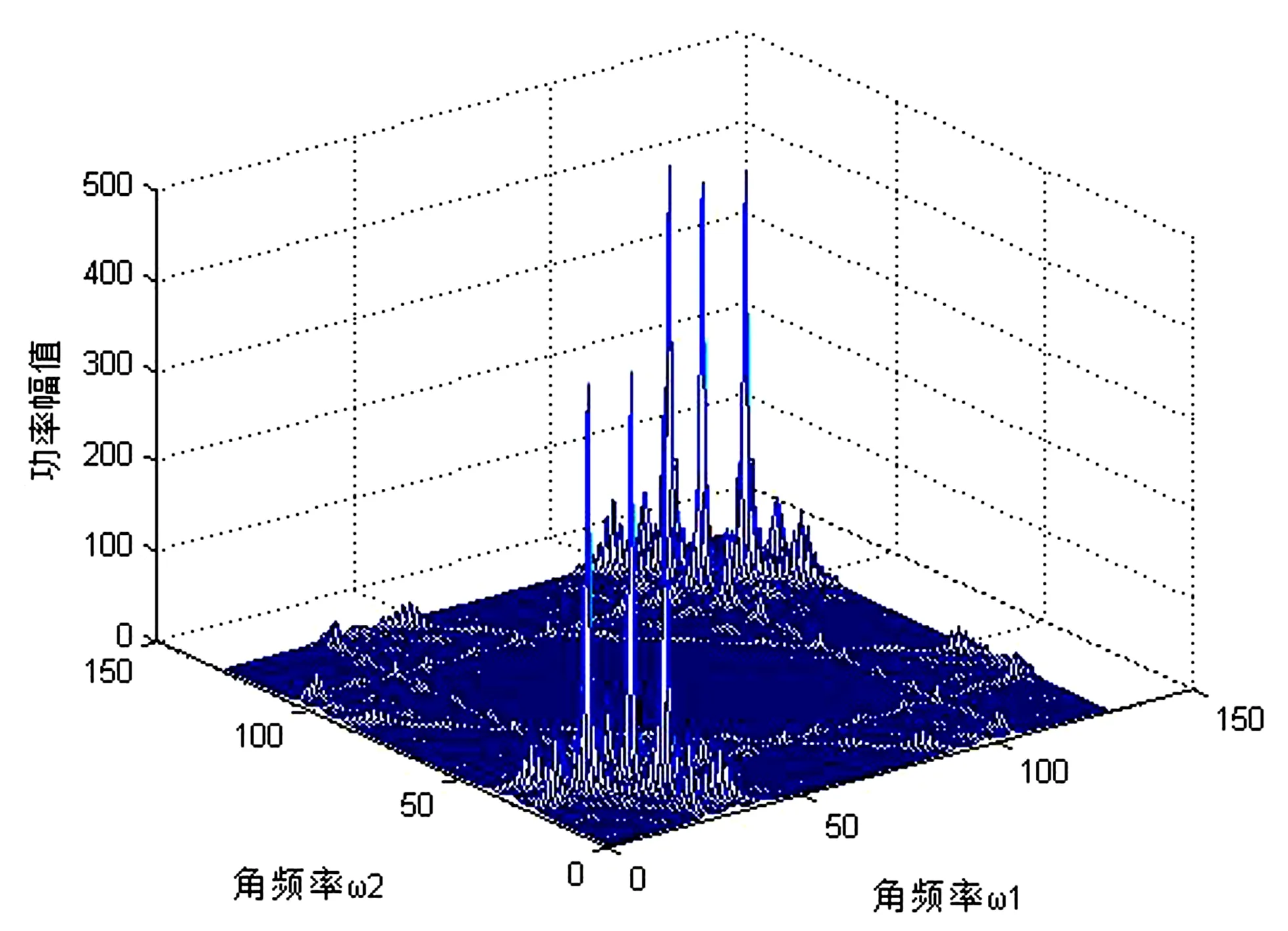
图4 加工后的蓝宝石表面二维功率谱图Fig.4 2D power spectrum of surface of sapphire after processing

在加工过的蓝宝石表面分别选取两个测试点(a和b)，得到取样长度内的表面形貌和功率谱分布如图5所示。

由图5可知，a和b测试点的表面形貌是不尽相同的，但两处的Ra值同为0.022μm。两处的表面形貌在宏观上虽比较相似，但仍有差异，所以对应的二维功率谱分布也是不相同的，且两处得到的关联维数分别为2.0131和2.8893。

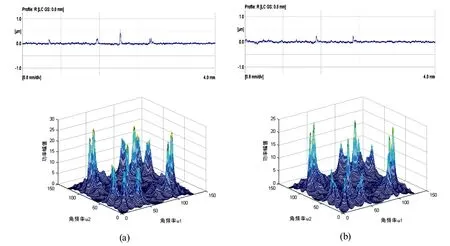
图5 单个取样长度形貌和其对应的功率谱图Fig.5 Morphology of individual sampling length and its corresponding power spectrum

4 结 论

传统的表面形貌参数不能准确表征整个蓝宝石晶片的表面形貌特征。本文通过运用二维功率谱和分形理论中的关联维数对蓝宝石晶片在未加工、金刚石磨粒抛光后的表面以及单个采样长度内的形貌进行了表征。蓝宝石微观表面越平坦，则其对应的二维功率谱波峰在任意两正交频率上的分布越均匀，关联维数越小。二维功率谱分布和关联维数包含了工件表面形貌多方面的信息，能够对其进行准确表征。

[1] 王银珍，彭观良，刘世良，等. 表面处理对蓝宝石衬底的影响[J]. 人工晶体学报，2005，34(3)：431-434.

[2] 王崇鲁. 白宝石单晶[M]. 天津：天津科技出版社，1983：16.

[3] 周兆忠，袁巨龙，文东辉.蓝宝石衬底的超光滑表面加工进展[J]. 航空精密制造技术，2009，45(3)：8-13.

[4] 马聪，黎明，王长坤. 机械加工表面粗糙度的视觉检测[J]. 南昌航空工业学院学报(自然科学版)，2003，17(3).

[5] 杨力. 先进光学制造技术[M]. 北京：科学出版社，2001.

[6] Campbell J H. NIF optical materials and fabrication technologies：An overview[J]. SPIE，2004，5341：84-101.

[7] Fang S J，Haplepete S，Chen W，et al. Analyzing atomic force microscopy images using spectral methods[J]. Journal of Applied Phys，1997，82(12)：5981-5998.

[8] Church E L. Fractal surface finish[J]. Applied Optics，1988，27(8)：1518-1526.

[9] 杨叔子，吴雅. 时间序列分析的工程应用(上)[M]. 武汉：华中科技大学，2007.

[10] 李成贵. 三维表面微观形貌的二维功率谱表征[J]. 计量学报，2004，25(1)：11-15.

[11] 李玉霞，吴百海，刑志鹏. 单变量时间序列相空间重构及应用研究[J]. 组合机床与自动化加工技术，2004，(2)：51-55.

[12] Grassberger P，Procaccia I. Charaterization of strange attractors[J]. Physical Review Letters，1983，50(5)：346-349.

Analysis of Power Spectrum and Fractal Characteristics of theSurface Topography of Sapphire

XU Yong-chao1,2, LU Jing1,2*, XU Xi-peng1,2

(1.InstituteofManufacturingEngineering,HuaqiaoUniversity,Xiamen,Fujian,China361021;2.MOEEngineeringResearchCenterforBrittleMaterialsMachining,HuaqiaoUniversity,Xiamen,Fujian,China361021)

The surface morphology of the sapphire wafer has been analyzed by 2D power spectrum and correlation dimension of fractal theory. The application of power spectrum calculation by 2D FFT (Fast Fourier Transform) in the surface morphology of sapphire has been introduced; phase space was reconstructed through time delay technology and the correlation dimension of the surface morphology of sapphire was calculated by G-P algorithm. The topographic characteristics of the original surface, processed surface and individual sampling length of sapphire were analyzed through experiment by 2D power spectrum and correlation dimension. Result shows that the surface morphology of sapphire can be characterized by 2D power spectrum and correlation dimension. It avoid the shortcoming of the traditional characterization parameter which contains only information on the vertical direction and can not accurately characterize the surface morphology of the entire sapphire wafer. This type of characterization method has the advantages of being accurate, convenient and informative compared to the traditional methods.

sapphire; 2D power spectrum; correlation dimension; surface topography

2016-09-12

许永超(1986-)，男，河南省辉县市，华侨大学制造工程研究院博士研究生，主要从事高效精密加工的研究。

许永超, 陆 静, 徐西鹏.蓝宝石表面形貌的功率谱与分形特征分析[J].超硬材料工程，2017，29(2)：56-60.

TS933;TQ164

A

1673-1433(2017)02-0056-05