基于连通性的无线传感器网络覆盖优化算法*
2017-05-10梅希薇宋鑫宏
梅希薇, 宋鑫宏, 方 伟
(江南大学 物联网工程学院,江苏 无锡 214122)
基于连通性的无线传感器网络覆盖优化算法*
梅希薇, 宋鑫宏, 方 伟
(江南大学 物联网工程学院,江苏 无锡 214122)
针对无线传感器网络(WSNs)的覆盖优化和连通性问题,提出了一种基于连通性的WSNs覆盖优化算法(CC—BCBS)。在二维监测区域内,CC—BCBS以传感器节点间的通信半径作为限制条件,只对连通的传感器节点进行Voronoi图划分,根据节点对应泰森多边形的覆盖情况构造盲区图,将盲区重心作为候选优化位置,使节点尽可能最大化覆盖监测区域。节点通信半径影响着区域覆盖的冗余度,故针对划分时可能出现的3种不同连通情况,给出了相应措施。仿真结果表明:CC—BCBS在覆盖率,分布均匀性,平均连通个数与连通率方面相比BCBS等算法有明显优势。
无线传感器网络; Voronoi图; 连通性; 覆盖优化
0 引 言
在无线传感器网络(WSNs)[1]的覆盖优化问题中,网络覆盖率和连通性是重要的性能指标,网络的覆盖率代表了传感器对目标区域的有效覆盖范围,连通性是网络进行可靠数据传输的基础。如何在达到网络覆盖最优化的过程中考虑连通性[2]等相关属性,成为目前研究覆盖控制方面的主要课题[3]。
很多专家学者从覆盖优化、连通,或两者综合的角度对WSNs进行了研究。文献[4]将NSGA-II进行改进用于混合WSNs覆盖优化算法。文献[5]提出的miniMax算法将泰森多边形最小外接圆圆心作为目标点,VOR算法中传感器节点向离其最远泰森多边形顶点移动。文献[6]提出的混合部署 (VEDGE) 策略,将泰森多边形最大内切圆圆心和最小外接圆圆心中覆盖率最高的位置,作为节点移动的目标位置。文献[7]采用ASFA算法增强大规模WSNs覆盖效果并延长其生存时间。文献[8]提出的二进制冲撞比特搜索(binary collision-bit search,BCBS)算法采用优化伪形心方式提升覆盖率,但未考虑传感器节点实际通信能力。文献[9]提出的基于连通度获得相对距离的非测距定位算法,大大提高了定位精度。文献[10]提出当节点的通信半径是其感知半径的2倍或以上时,对目标区域保持全覆盖的活跃节点集是全连通的。
针对WSNs的连通和覆盖优化问题,在前期研究的BCBS的基础上,提出了一种基于连通性的WSNs覆盖优化算法研究(connectivity-considered BCBS,CC-BCBS)。与BCBS,CBS[11],VEDGE[5]等算法进行对比实验,结果表明:CC-BCBS算法在覆盖率、分布均匀性、连通个数、连通率的性能中优势明显。
1 无线传感器覆盖优化模型
在大小为L×W的二维平面监测区域T内(L和W分别监测区域的长和宽),通过随机部署的方式在T内放置N个传感器节点,得到传感器节点集合为D={d1,d2,…,dN}。Di(i∈N)的感知范围是以该节点为圆心,半径等于感知半径Rs的一个圆形区域,用位置坐标为di(xi,yi),di={p∈L×W|ds(p,Si)≤Rs}表示,其中ds(p,Si)为点p与点Si的欧氏距离,传感器网络的覆盖范围C是网络中所有活动节点的覆盖范围的并集。Rc表示通信半径,文献[12,13]证明,当Rc≥2Rs时,两个传感器节点是可以通信的。二维平面监测区域分成a×b个网格,每个网格的交点位置为目标点位置。将传感器节点通过一定的方式在监测区域内移动,在减小重叠区域、缩小盲区范围的同时,提高传感器节点在监测区域内的覆盖率。
WSNs覆盖性能指标一般包括覆盖率、覆盖效率、分布均匀性、连通率。
覆盖率CR定义为所有传感器节点的覆盖面积之和与目标区域面积的比值,覆盖率总是小于或等于1[14]。
(1)
式中 CR为覆盖率;Ci为第i个节点的覆盖面积;N为节点的个数;A为整个目标区域的面积。
平均连通个数AN在本文中定义为迭代后全连通个数与总迭代次数的比值,即
(2)
式中 AN为平均连通个数;M为迭代次数;Am为每次迭代达到全连通的传感器个数。
连通率CN即传感器节点达到全连通的平均迭代次数与总迭代次数的比值,反映了传感器节点连通性能的好坏,即
(3)
式中 CN为连通率;N为运行次数;M为迭代次数;Cm为第m次迭代时传感器节点是否全连通。Cm为个布尔型变量,若连通则Cm=1;否则,Cm=0。
分布均匀性U反映了节点在监测区域的分布情况,U越小节点分布越均匀,定义为传感器节点与其邻居节点之间距离的标准差的均值[15]。
(4)
(5)
(6)
Di,j=d(si,zj)
(7)
式中 ki为第i个节点的邻居节点个数;Mi为第i个节点与邻居节点的平均距离;Di,j为第i个节点与第j个邻居节点之间的距离;Ui为传感器节点di与其邻居节点Z之间距离的标准差。
2 CC-BCBS算法
2.1BCBS算法
Voronoi图是划分传感器节点的有效方式,传感器节点数量与感知范围的大小影响其在监测区域内的覆盖部署效果,如果覆盖率未达到100 %,则必然存在未覆盖区域,称之为感知盲区[16]。BCBS算法对感知盲区的处理方法是构造与泰森盲区多边形[8]。用传统泰森多边形法时,如果在部署过程中未考虑邻居节点对当前传感器节点的影响,则会产生伪形心[7]。BCBS算法对此进行改进,并依据泰森多边形顶点覆盖情况讨论盲区的形状:泰森多边形顶点全覆盖时,盲区顶点为邻居节点与当前感知圆盘[17]交点,如图1(a)中虚线表示新的传感器与周围邻居节点感知圆盘的交点(1,2,3,4)围成的多边形,实心三角形为多边形形心位置,原泰森多边形形心位置用叉表示,通过比较在不同形心位置的覆盖率来选择最佳部署节点位置;泰森多边形顶点部分覆盖时,如图1(b)所示,盲区顶点由两部分组成,一部分为已覆盖顶点的邻居节点与当前感知圆盘交点(3,4,5),另一部分为未覆盖的顶点(1,2)所围成的多边形;泰森多边形顶点都没被覆盖时,盲区为当前传感器所在泰森多边形的顶点。继而通过对盲区形心和伪形心位置的选取,来提高监测区域的覆盖率。该算法虽然提高了传感器节点的覆盖率,但是未考虑是否在全连通的情况下进行有效信息传输。
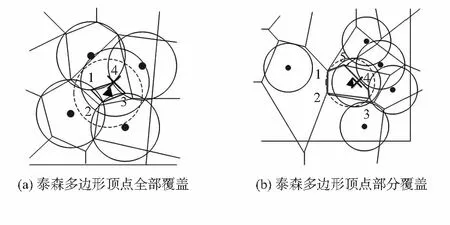
图1 泰森多边形顶点全部覆盖和部分覆盖
2.2 连通性与Voronoi图划分的关系
在给定的监测区域范围内,传感器的通信半径以及个数等参数设置对网络中节点的部署效果起到了一定的影响:如图2(a)所示,传感器个数不变的情况下,传感器的通信半径过小难使网络快速连通。而图2(b)中通信半径设置过大,则网络很容易达到饱和,不同节点直接相互干扰性强,不利于节点向正确方向的移动。
本文中利用三角剖分生成Voronoi图[18],孤立节点表示与所有邻居节点的通信半径均小于2倍感知半径的点。当有一个孤立节点时,则在划分Voronoi图时去掉该点及其邻居节点的关联信息。由于2个节点无法构成三角网,故本文规定当只有2个节点可相互通信时等待被传唤,暂不进行划分。当有大于2个可通信节点时,进行Voronoi图划分。如图3所示,节点13,16,19,27为孤立节点,无法与其他节点通信,故在划分Voronoi图时去这些点。如节点4,7只能互相通信,故不进行Voronoi图划分;节点2,15,26,29,30中可通信节点的数量大于2,故将参与Voronoi图划分。
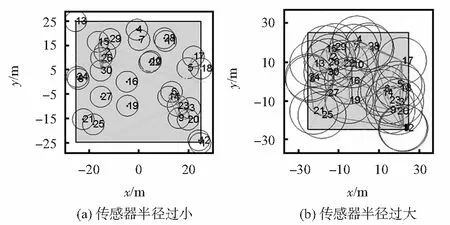
图2 传感器部署效果
2.3 CC-BCBS算法描述
传感器感知半径同构且感知范围有限的情况下,用合适的的节点数尽可能最大化覆盖监测区域,即监测区域中每个传感器节点有效覆盖区域面积最大,减少感知圆盘之间的重复部分,从而充分利用每一个感知圆盘。由文献[10]可知,3个半径相同的圆相交于一点,当圆心构成的三角形是等边三角形时,这些圆构成的总圆域对监测区域的覆盖范围最大。
本节提出的基于连通性的WSNs覆盖优化(CC-BCBS)算法,是在之前提出的BCBS算法优化网络覆盖率的基础上,为了提高传感器节点的连通率和分布均匀性,考虑了传感器感知半径的大小对其在监测区域内数量分布的影响,且以通信半径为前提,针对部署过程中可能产生的3种不同的连通情况从而进行Voronoi图划分。该算法不仅兼顾了连通性、分布均匀性,还使覆盖率得到了提高,具体描述如下:
1)随机部署传感器节点的初始位置,得到传感器节点集D={dc1,dc2,…,dcn,dpq,…,dpn},dci为可通信节点,dpi为不可通信节点。节点间距离矩阵Dmk={d11,d12,…d1k;…;dm1,dm2,…,dmk},dmk表示第m和第k个节点的距离。
2)用2.2节阐述的划分方式在保证dmk≥2Rs前提下构造初始Voronoi图(Rs为感知半径)。
3)当前节点di与邻居节点组成节点集Di=D_i{di,z1,z2,…,ze},Di对应的泰森多边形集合为Vk={vi,vz1,vz2,…,vze},其中e是邻居节点个数。依据泰森多边形顶点覆盖情况判断是否存在盲区:若当前节点di全被覆盖,说明不存在泰森盲区,转步骤(8);否则,存在泰森盲区(盲区为2.1节阐述的泰森多边形顶点部分被覆盖和全都未被覆盖时所对应的形状),继续进行下一步骤。
4)得到当前节点di在当前位置(dx,dy)对应的初始局部覆盖率qi。
5)得到当前节点di在盲区重心wi处对应覆盖率ti,并将wi作为最优候选位置。
6)限制最大移动步长:若wi与di距离dwi_di大于最大步长,则将两点所连线段上与wi距离为Maxstep的点赋值给wi,wi=(wx,wy)。求其新的局部覆盖率ti。
7)比较覆盖率ti和qi:如果qi≤ti,则用盲区重心位置(wx,wy)替换掉原来的节点位置作为当前节点位置,即di=(wx,wy);否则节点位置不变,即di=(dx,dy),转步骤(10)。
8)在Di内删去节点di,得到邻居节点集Ze={z1,z2,…,ze},在保证Di内两个传感器节点间的距离大于或等于2倍感知半径的前提下重构Voronoi图,由邻居节点集Ze形成新的泰森多边形V'e={v'z1,v'z2,…,v'ze}。
9)计算V'e内新产生泰森多边形顶点覆盖情况,若新顶点全被覆盖,说明不存在泰森盲区,计算V'e的重心wi=(wx,wy),则用新找到的重心位置(wx,wy)更新原来的节点位置,即di=(wx,wy),进入下一步骤。否则,存在泰森盲区(盲区为上节讨论的泰森多边形顶点部分被覆盖和全都未被覆盖时所对应的形状),转步骤(4)。
10)重复步骤(3)~(9),直到所有节点都执行完为止。
11)重复步骤(2)~(10),直到满足停止条件。
以下显示了在二维矩形平面内CC-BCBS的某一次部署全过程。

表1 仿真环境参数
图3(a)~ (c)展示了CC-BCBS算法在迭代过程中传感器节点的分布图,点代表传感器节点,圆圈代表每个传感器节点的感知范围,线表示对区域进行Voronoi图划分。30个节点的初始覆盖率为74.12 %(图3(a)),此时节点19无法通信,则在划分Voronoi图时去掉该点以及其邻居节点25,27,16,14,3,12的关联信息。18次迭代后为97.93 %(图3 (b)),最终覆盖率为98.61 %(图3(c))。可以看出由最初的散乱分布到最终均匀分布,且在迭代早期传感器分布情况较优。
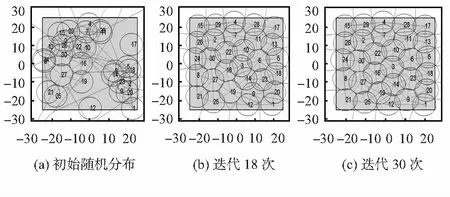
图3 一次迭代部署过程
3 实 验
本次实验从覆盖率、分布均匀性、平均连通个数、连通率来对CC-BCBS等6种算法实验结果比较如图4。共进行30次随机部署实验,每次迭代30次,实验参数与表1相同。
图4为传感器节点覆盖率变化曲线,该曲线图表明了在算法运行初期,CC-BCBS的覆盖率效果提升快,且在第3次运行时其覆盖率就已经超过其他5种算法,算法最终覆盖率达到98.14 %并趋于稳定,故CC-BCBS算法在该性能中占优。由于分布均匀性数值越低越好,由图4(b)知,CC-BCBS平均分布均匀性为1.277 2,故在该性能中占优。
图4(a)表明CC-BCBS和VOR 2种算法在迭代完成后连通个数最多(平均连通个数为30)且处于全连通状态,BCBS算法平均连通个数是29.35,CC-BCBS和VOR算法在该性能中占优。图4(d)表明CC-BCBS和VOR算法连通率达100 %,BCBS在每次运行中连通率都有所变化但变化不大,CBS,VEDGE和miniMax次之。
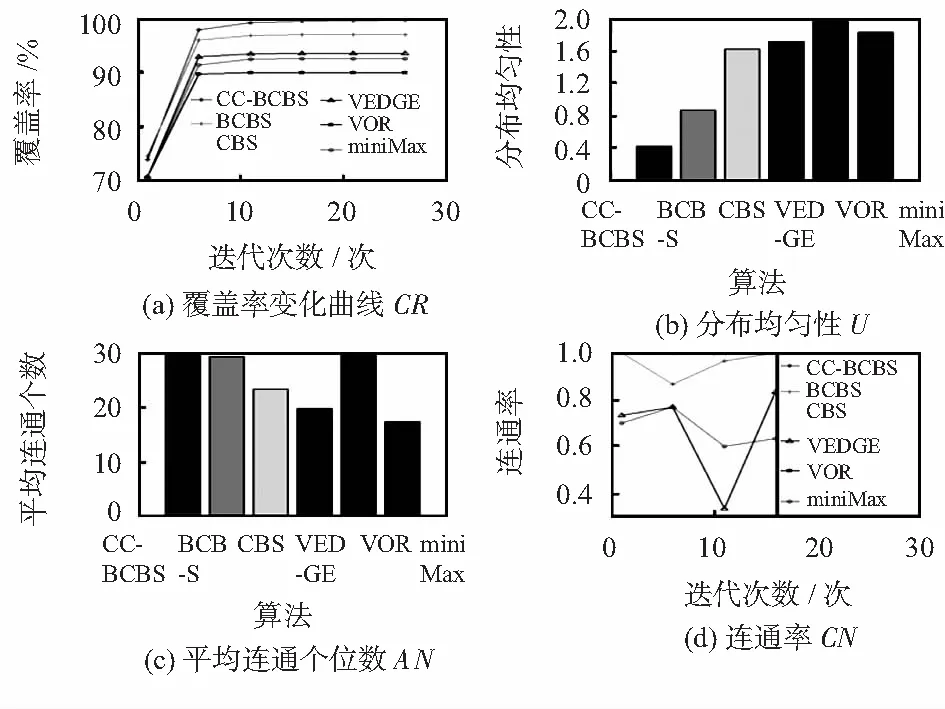
图4 6种算法实验结果比较
4 结束语
本文提出的基于连通性的WSNs覆盖优化算法,具有连通性强、覆盖率高、节点分布均匀性好的优点。在相同的环境参数下,由于传感器节点随机部署位置的不同,算法结果也对应有所变化,虽然达到了全连通,但在初次达到全连通的代数上还是有改进的空间,而且覆盖率还有提升空间。将本文提出的算法用于不规则监测区域以及三维空间也是下一步的研究方向。
[1] 霍慧慧,李国勇.改进的离散果蝇优化算法在WSNs覆盖中的应用[J].传感器与微系统,2016,35(2):157-160.
[2] 翟正怡.无线传感器网络中的覆盖优化算法与连通问题研究[D].上海:同济大学,2008.
[3] 赵 旭,雷 霖,代传龙.无线传感器网络的覆盖控制[J].传感器与微系统,2007,26(8):62-66.
[4] 祁育仙,李国勇.混合WSNs中基于多目标优化的覆盖控制算法[J].传感器与微系统,2016,35(2):136-139.
[5] Wang G,Cao G,Porta T F L.Movement-assisted sensor deployment[J].IEEE Transactions on Mobile Computing,2006,5(6):640-652.
[6] Mahboubi H,Moezzi K,Aghdam A G,et al.Distributed deployment algorithms for efficient coverage in a network of mobile sensors with nonidentical sensing capabilities[J].IEEE Transactions on Vehicular Technology,2014,63(8):3998-4016.
[7] 仲元昌,陈 锋,李发传,等.大规模无线传感器网络覆盖优化算法[J].传感器与微系统,2014,33(11):117-120.
[8] 方 伟,宋鑫宏.基于Voronoi图盲区的无线传感器网络覆盖控制部署策略[J].物理学报,2014(22):132-141.
[9] 徐磊磊,徐保国.无线传感器网络中一种基于连通性的非测距定位算法[J].传感器与微系统,2016,35(1):127-130.
[10] Xing Guoliang,Wang Xiaorui.Integrated coverage and connectivity configuration for energy conservation in sensor networks[J].ACM Transactionson Sensor Networks,2005,1(1):36-72.
[11] Lee H J,Kim Y H,Han Y H,et al.Centroid-based movement assisted sensor deployment schemes in wireless sensor network-s[C]∥Proceedings of the 2009 IEEE 70th Vehicular Technology Conference Fall(VTC 2009-Fall),IEEE:Piscataway,NJ,2009:89-91.
[12] Zhang H H,Hou J C.Maintaining sensing coverage and connecti-vity in large sensor networks[J].Ad Hoc & Sensor Wireless Networks,2004,1(2):1097-1100.
[13] Tian D,Georganas N D.Connectivity maintenance and coverage preservation in wireless sensor networks[C]∥Canadian Confe-rence on Electrical and Computer Engineering,2004:1097-1100.
[14] 曾映兰,陈 静,郑金华.基于遗传算法的WSNs覆盖优化方法[J].计算机工程与应用,2009,45(11):89-91.
[15] 刘丽萍.无线传感器网络节能覆盖[D].杭州:浙江大学,2006.
[16] Yue X,Yu J,Zhao M.PBADaPCo:An efficient algorithm based on improved edge weighted voronoi diagram to detect and make-up potential blind areas in wireless sensor networks[C]∥Proceedings of 2008 the 3rd International Conference on Innovative Computing Information and Control,IEEE Computer Society,2008:589.
[17] 任永功,廖士中.利用类Delaunay三角剖分实现Voronoi图[J].计算机科学,2002,29(9):78-79.
Connectivity-based coverage optimization algorithm for WSNs*
MEI Xi-wei, SONG Xin-hong, FANG Wei
(School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,China)
Aiming at problem of coverage optimization and connectivity in wireless sensor networks(WSNs),a connectivity considered-BCBS(CC-BCBS)is proposed.In two-dimensional monitoring region,CC-BCBS uses communication radius as restriction condition, and just partitions connected sensor nodes by Voronoi diagram.CC-BCBS constructs the blind-zone area according to different coverage means of Voronoi polygon,and sets the centroid of the blind-zone as the optimal candidate position so as to improve the coverage rate.The influence that communication radius has on coverage redundancy is considered.Reasonable measures areshowed in case of three kinds of connectivity cases that might occur when doing partitions.Simulation results show that the algorithm has obvious advantages in coverage rate,distribution uniformity,average connect number and connectivity rate compared with algorithm like BCBS and so on.
wireless sensor networks(WSNs); Voronoi diagram; connectivity; coverage optimization
10.13873/J.1000—9787(2017)05—0145—04
2016—05—29
国家自然科学基金资助项目(61105128,61170119,61373055);江苏省自然科学基金资助项目(BK20131106,BK20130161);江南大学自主科研计划重点项目(JUSRP51410B);中国博士后基金资助项目(2014M560390)
TP 393
A
1000—9787(2017)05—0145—04
梅希薇(1992-),女,硕士,研究方向为无线传感器网络覆盖控制优化算法。
方 伟(1980-),男,通讯作者,博士,主要从事计算智能、无线传感器覆盖优化的研究,E—mail:fangwei@jiangnan.edu.cn。
