基于神经网络滑模的智能车辆横向控制*
2017-05-10陈涛,陈东
陈 涛, 陈 东
(湖南大学 汽车车身先进设计制造国家重点试验室,湖南 长沙 410082)
基于神经网络滑模的智能车辆横向控制*
陈 涛, 陈 东
(湖南大学 汽车车身先进设计制造国家重点试验室,湖南 长沙 410082)
以智能车辆为研究对象,针对车辆模型存在高度非线性动态特性、参数不确定性以及行驶时受外部干扰较多导致控制精度不高、鲁棒性差等问题,提出了采用径向基函数(RBF)神经网络滑模控制方法。建立2自由度线性车辆模型和自由度非线性整车模型,在传统2自由度车辆控制模型状态方程的基础上推导出新的状态方程并以此设计了相应控制器。利用李雅普诺夫(Lyapunov)稳定性理论推导出神经网络的权,并证明控制系统的稳定性。仿真结果表明:与传统的滑模控制方法相比,该方法控制精度高,有较强的鲁棒性。
智能车辆; 神经网络; 滑模控制; 横向控制
0 引 言
随着汽车工业的发展以及科技的不断进步,车辆驾驶辅助设备逐渐进入人们的视野,如车道保持系统、道路偏离预警系统、主动避撞系统等,都涉及对车辆的横向控制。横向控制[1]是指车辆通过机器视觉、激光雷达或全球定位系统(GPS)等传感器获得反馈的信息,按照一定的控制策略使车辆沿着指定的路径行驶。因为车辆存在高度非线性、模型不确定性以及受外部干扰较多等问题,所以,对车辆的横向控制一直以来都是国内外学者研究的重点之一。郭景华和胡平等人[2]提出了基于遗传优化的模糊控制方法,通过遗传算法对横向模糊控制器的隶属度函数参数和控制规则自动优化,并通过仿真和实车进行了验证,该方法在低速时效果较好,随着车速的增加,车辆模型与实际情况偏差会逐渐增大,导致控制效果变差。赵熙俊和陈慧岩等人[3]设计了一个鲁棒PID控制器用来提高系统的瞬态响应。该方案设计较为简单、易于实现,但对于外界路面的复杂情况存在确定参数困难,难以实现自适应控制等不足。王家恩和陈无畏等人[4]提出了跟踪期望横摆角速度的车辆横向控制方法并设计了滑模控制器跟踪目标路径。目标路径由车辆当前位置和预瞄点之间实时规划产生,但是车辆的实时横摆角速度在实际中较为难测,因此,该方法可行性较低。Gregor和Igor[5]提出了一种基于模型预测轨迹跟踪的控制方法,使用线性化动态跟踪误差来预测未来的系统行为。但是当存在较大跟踪误差时,系统的鲁棒性存在不足,自适应较差。Soualmi和Sentouh等人[6]采用了模糊T-S(Takagi-Sugeno)控制方法,通过控制方向盘转矩来追踪期望路径,但是其控制力矩抖振较为严重,在实际应用中容易造成车辆机械结构的磨损。Onieva和Naranjo等人[7]设计了一种利用遗传算法优化的模糊控制器,在直线道路上,控制较为精确,但在曲线道路上性能表现较差。
近些年,部分学者提出了滑模控制方法[8~10],设计横向控制器,它具有鲁棒性较强、系统响应快、不需要精确的模型等优点。但是在滑模面附近由于高频转换控制会产生高频抖振现象,这种抖振会影响控制的精确性,严重时会使系统产生振动或失稳造成车辆的机械磨损和硬件电路的损坏。径向基函数(RBF)神经网络是一种局部逼近神经网络,能任意精度逼近任意连续函数。
基于以上原因,本文提出了RBF神经网络滑模控制方法,结合两者优点,减少系统产生的抖振。同时,以上研究未曾考虑模型不确定性、非线性和外界干扰较大的情况,本文通过RBF神经网络逼近不确定的外部干扰和建模误差,使得控制更为精确同时增强系统的鲁棒性。
1 控制系统结构设计
控制系统的设计目的是通过控制前轮转角使得车辆与期望路径的偏差迅速缩减为零。本文的控制系统结构框图如图1所示。前轮转角由控制器输出给整车模型,通过与理想状态对比,确定此时车辆的偏差,作为控制器的其中一个输入参数。RBF神经网络通过逼近外界的干扰项以及建模误差实现自适应控制。自适应律由李雅普诺夫稳定性原理推导得出,并证明了控制器的稳定性。
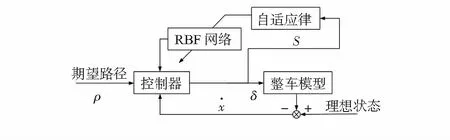
图1 控制系统结构框图
2 车辆横向控制模型
2.1 车辆二自由度运动模型
控制器的设计以二自由度转向模型为基础。根据文献[11]对实际车辆假设如下:1)忽略转向机构的影响,将前轮转角作为输入,且认为左右车轮转角大小一样;2)忽略车辆悬架对车辆运动特性的影响,忽略车辆垂直、俯仰、侧倾运动,将车辆运动看作是与地面平行的平面运动;3)忽略左右车轮轮胎由于载荷变化引起的轮胎侧偏特性的差异。根据假设,车辆在行驶过程中,轮胎与地面不存在侧向滑动且左右轮胎动力学对称,则每个车轴上的2个车轮可以用1个车轮来代替,这样车辆就简化为二轮车辆模型。

图2 二自由度车辆转向模型
根据牛顿第二定律,得到车辆的横向动力学方程为
(1)
(2)
式中m为车辆质量;Cf,Cr为前后轮胎侧偏刚度;Iz为车辆转动惯量。
2.2 整车七自由度运动模型
为了使仿真的数据与实际情况更接近,整车模型采用更具代表性的七自由度4轮模型,如图3所示。由此建立整车模型如下:
1)纵向动力学方程
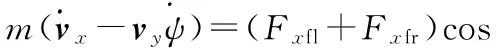
(Fyrl+Fyfr)sinδf
(3)
2)横向动力学方程
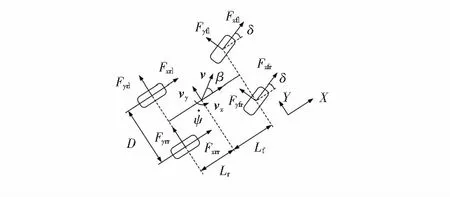
图3 七自由度车辆动力学模型

(Fyfl+Fyfr)cosδf
(4)
3)横摆运动方程
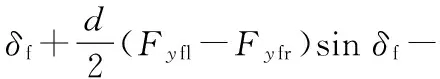
(5)
2.3 轮胎模型
本文所采用的Dugoff轮胎模型[12]属于理论模型,相对其他轮胎模型,Dugoff模型对精确轮胎参数的依赖性更小,而仿真精度较高。
轮胎纵向力和侧向力分别为
Fxij=fijkxijSij
(6)
Fyij=fijkyijαij
(7)
(8)
(9)
整车质心侧偏角为
(10)
各轮胎的滑移率分别为
(11)
各轮胎的侧偏角分别为
(12)
(13)
各个轮胎的垂直载荷为
(14)
(15)
(16)
(17)
式中Fxij,Fyij为轮胎的纵向力和侧向力;kxij,kyij为轮胎纵向和侧向的侧偏刚度;αij为轮胎的侧偏角;μHij为轮胎与路面最大附着系数;re为车轮滚动半径;wij为车轮滚动角速度;uij为车轮中心速度;ax为纵向加速度;ay为横向加速度;h为质心高度。
2.4 控制问题描述
通过传感器采集当前车辆信息确定出与期望路径的偏差e。
对于给定的参考路径会有
(18)
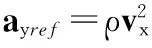

(19)
联合公式(1)、式(2)、式(19)得到控制系统的状态方程
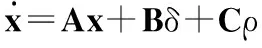
(20)
式中 状态变量为

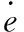
(21)
(22)
此时控制输入为
(23)
在此基础之上,定义新的误差
(24)
则新的控制器的状态方程变为
x~=Ax~+Bδ~
(25)
考虑到车辆在行驶时的外界干扰以及系统的建模误差,控制器的设计根据x~=Ax~+Bδ~+D设计。
3 神经网络滑模控制器设计
3.1 滑模变结构控制
滑模控制器[14]的设计包括滑模面s(t)和滑模函数u(t),其作用,首先,将空间某一状态在控制作用下运动到所设计的滑模面上,然后设计一个控制律保证被转移到滑模面上的点始终在滑模面上运动,并在有限的时间内到达原点。定义滑模面的形式为
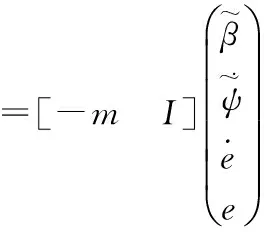
(26)

δ~=-(MB)-1(MAx~+MD+ks(t)+ζsgn(s(t))
(27)
在实际工况中,外界干扰不可知,同时存在建模误差,为此采取RBF神经网络进行逼近。RBF神经网络[15]为3层前馈式网络结构,包括输入层、中间层和输出层。结构中,RBF网络的输出,即
(28)
式中m为隐含层神经个数;w为权值;h为高斯基函数,其表达式为
(29)
式中xi为输入;cj=|cj1cj2|为中间层第j个神经元高斯基函数中心点的坐标向量;bj为隐含层第j个神经元高斯基函数的宽度。
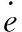
3.2 稳定性分析

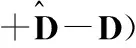
=-ks-ξsgn(s)+M(-W~Th+ε)
(30)
针对本文的设计的控制器,构造Lyapunov函数为
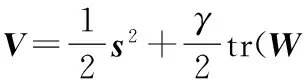
(31)
对Lyapunov函数求导得

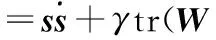
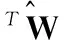
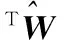
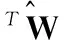

(32)
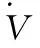
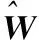
(33)
4 仿真试验分析
4.1 算法有效性分析
为验证本文所提出控制方法的有效性,本文在Matlab2014a平台下进行了仿真试验,具体车辆参数设置为:整车质量m为1 850 kg;前、后轮胎侧偏刚度Cf,Cr为62 850,72 000 N·rad-1;整车绕z轴转动惯量IZ为2 549 kg·m2;质心至前、后轴距离Lf,Lr为1.142,1.563 m;质心高度h为0.512 m;轮距D为1.25 m。
将神经网络滑模控制器和单一滑模控制器的控制效果进行仿真对比,参数设置相同,速度设为vx=10 m/s,k=10,ξ=1。图4(a)为横向偏差的响应曲线对比图,图4(b)为横摆角速度偏差响应曲线对比图。

图4 横向偏差和横摆角速度偏差响应曲线对比图
由图4可知,采用神经网络滑模控制器相比单一滑模控制有更好的表现,具有响应速度快,抖振小,能够迅速消除横向偏差等优点。表1为两种控制器仿真实验数据。

表1 单一滑模控制器和神经网络滑模控制器仿真实验数据
从表1可以看出,采用神经网络滑模比单一滑模的控制精度更高。本文以横向平均偏差作为控制器的控制精度,则控制精度提高了11 %。
4.2 算法鲁棒性分析
由图5(a)可知:随着纵向速度增快,横向偏差会相应增大,但在短时间内偏差会迅速收敛,说明本文提出的控制算法对车速变化有较强的适应性,收敛速度较快。

图5 不同速度、不同载荷以及带有外部干扰时的横向偏差响应曲线
由图5(b)看出:控制器对于载荷的变化同样具有较好的鲁棒性,横向偏差均在较小的范围内变化。为了进一步验证系统鲁棒性,在仿真实验中加入了正弦函数作为外部干扰,两种控制器的仿真结果对比如图5(c)所示。
由图5(c)看出:单一滑模控制器在有外部干扰的情况下误差较大较神经网络滑模控制器则有较强的适应能力,鲁棒性较好。
5 结 论
1)构建了车辆二自由度和七自由度动力学模型,对车辆横向控制系统的状态方程进行了描述,并推导出新的控制系统状态方程。
2)提出了神经网络滑模控制方法解决车辆横向控制问题。设计了神经网络滑模控制器,通过RBF神经网络实现对外界干扰和建模误差的逼近,利用Lyapunov函数推导了神经网络权值的自适应律,并证明了系统的稳定性。
3)仿真结果表明:本文所提方法能够有效降低滑模控制的抖振现象,同时,对外界干扰和建模误差等能够有效抑制,有较高鲁棒性。
[1] 李舜酩,沈 峘,毛建国,等.智能车辆发展及其关键技术研究现状[J].传感器与微系统,2009,28(1):1-3.
[2] 郭景华,胡 平,李琳辉,等.基于遗传优化的无人车横向模糊控制[J].机械工程学报,2012,48(6):76-82.
[3] 赵俊熙,陈慧岩.智能车辆路径跟踪横向控制方法的研究[J].汽车工程,2011,33(5):382-387.
[4] 王家恩,陈无畏,王檀彬,等.基于期望横摆角速度的视觉导航智能车辆横向控制[J].机械工程学报,2012(4):108-115.
[5] Gregor Klancar,Igor Skrjanc.Track-error model-based predictive
control for mobile robots in real time[J] .Robotics and Autonomous System,2007,55:460-469.
[6] Soualmi B,Sentouh C,Popieul J C,et al.Fuzzy takagi-sugeno LQ controller for lateral control assistance of a vehicle[C]∥International IEEE Conference on Intelligent Vehicles(IV)Symposium,2007.
[7] Onieva E,ENaranjo J,Milanes V,et al.Automatic lateral control for unmanned vehicle via genetic algorithms [J].Applied Soft Computing,2011,11:1303-1309.
[8] Zheng Shuibo,Tang Houjun,Han Zhengzhi,et al.Control design for vehicle stability enhancement [J].Control Engineering Practice,2006,14:1413-1421.
[9] Imine H,Madani T.Sliding-mode control for automated lane gui-dance of heavy vehicle[J].International Journal of Robust and Nonlinear Control,2013, 23:67-76.
[10] Gilles Tagne,Reine Talj,Ali Charara.Higher-order sliding mode control for lateral dynamics of autonomous vehicles,with experimental validation[C]∥International IEEE Conference on Intelligent vehicles(IV)Symposium,2013:67-76.
[11] 喻 凡,林 逸.汽车系统动力学[M].北京:机械工程出版社,2005.
[12] 皮大伟,陈 南,张丙军.基于主动制动的车辆稳定性系统最优控制策略[J].农业机械学报,2009,40(11):1-6.
[13] Rajesh Rajamani.Vehicle dynamics and control[M].Berlin/Heidelberg:Springer,2012.
[14] 于 驰,宫明龙.多输入多输出系统的滑模控制器设计及其应用[J].东北大学学报:自然科学版,2012,33(2):187-190.
[15] Fei Juntao,Ding Hongfei.Adaptive sliding mode control of dyna-mic system using RBF neural network[J].Nonlinear Dynamics,2012,70:1563 -1573.
Lateral control of intelligent vehicle based on neural networks sliding mode*
CHEN Tao, CHEN Dong
(State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University,Changsha 410082,China)
The RBF neural networks sliding mode control method is proposed to solve the highly nonlinear dynamic characteristic and parametric uncertain properties of the intelligent vehicle model as well as the low control precision and poor robustness caused by massive external interference during driving.A two degrees of freedom(DOF)linear vehicle model is built along with a seven DOF non-linear vehicle model.A new state equation is derived based on traditional state equation of the two DOF vehicle control method and the corresponding controller is designed.The Lyapunov stability theory is involved to derive the weights of the neural network and the stability of the control system is verified.Simulation results show that the proposed method has higher control precision and stronger robustness compared with the traditional sliding mode control method.
intelligent vehicle; neural networks; sliding mode control; lateral control
10.13873/J.1000—9787(2017)05—0063—05
2016—05—31
国家自然科学基金资助项目(61540031);湖南省自然科学基金资助项目(14J3055);中国博士后科学基金资助项目(2014M552132);国汽(北京)开放基金资助项目(20130303);中美清洁能源项目(2014DFG71590—101);中央高校基本科研业务费资助项目
U 461.91
A
1000—9787(2017)05—0063—05
陈 涛(1978-),男,硕士生导师,副教授,主要从事汽车主被动安全、汽车CAE技术、空气动力学等工作。
陈 东(1990-),男,通讯作者,硕士研究生,主要研究方向为主安全、汽车电子,E—mail:chen.dong1990@163.com。
