移动机器人车轮打滑检测与校核方法*
2017-05-10赵帅鹏李泉溪
赵帅鹏, 李泉溪, 薛 霄, 申 芳
(河南理工大学 计算机科学与技术学院,河南 焦作 454003)
移动机器人车轮打滑检测与校核方法*
赵帅鹏, 李泉溪, 薛 霄, 申 芳
(河南理工大学 计算机科学与技术学院,河南 焦作 454003)
针对移动机器人车轮打滑引起的非系统误差,提出了双轮检测结构模型。利用检测轮与驱动轮编码器输出脉冲数,建立直行和不同转向方式的车轮打滑模型并给出打滑辨识算法。利用正向校正算法或反向校正算法校正运行方向误差与位移误差。仿真结果表明:该结构模型能够累计机器人长时间运行产生的打滑误差,并实时校正,反向校正算法存在极少的位移误差,校正精度优于正向校正算法,但正向校正算法逻辑简单,能量消耗少。
双轮检测结构; 打滑模型; 正向校正; 反向校正
0 引 言
轨迹推算定位算法在移动机器人定位领域被广泛使用[1]。在没有外界参考的情况下,该算法能够实现短时间内的高精度定位,其缺点在于随着工作时间增加而增加的累计误差。针对系统误差,Borenstein J和Feng L提出的UMBmark校正方法[2],使移动机器人的定位精度(相对于系统误差)至少提高了1个数量级。因此,由车轮打滑引起的非系统误差成为主要的误差源[3]。
针对车轮打滑,Ibraheem M[4]采用扩展卡尔曼滤波(EKF)将编码器和陀螺仪结合,降低了非系统误差对机器人定位的影响,提高了系统的稳定性;Cho B等人[5]利用卡尔曼滤波将编码器、电子罗盘和陀螺仪融合,有效降低了轨迹推算定位算法的累计误差。这些方法中,电子罗盘容易受到电磁干扰,使用时受环境限制,陀螺仪存在漂移误差,且实现算法复杂,对处理器性能要求高[6]。
本文提出的双轮检测结构模型能够实时辨别机器人运行时打滑,并计算出车轮打滑引起的方向误差,根据误差校正阈值,判定是否利用正向校正算法或反向校正算法校正运行误差,该结构模型提高了系统的稳定性且有效降低了驱动轮打滑引起的累计误差。
1 双轮检测系统总体设计
根据相对位移思想设计了双轮检测结构模型。检测轮与驱动轮在同一轴线上,且采用中心对称结构。双轮检测结构模型如图1所示。
双轮检测结构模型的控制由中央控制器实现,中央控制器完成的主要任务有:电机转向控制、编码器输出脉冲计数、打滑模型辨别、运行误差计算。该结构的驱动系统与机械设计由文献[7]提出的设计方法实现。
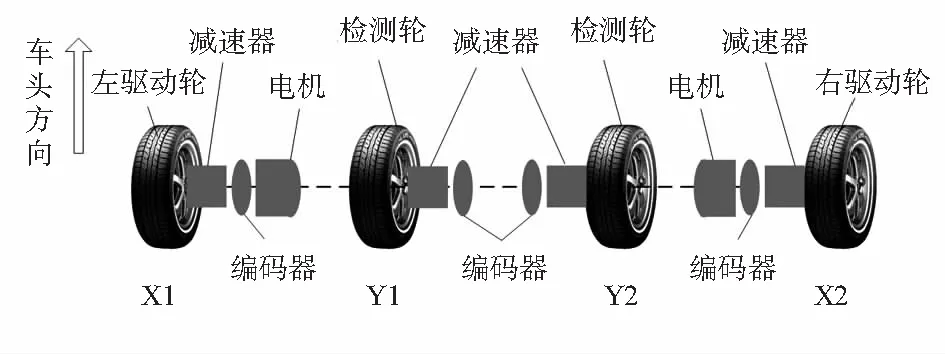
图1 双轮检测结构模型
机器人在行驶过程中,如果驱动轮打滑,驱动轮编码器输出的脉冲数不受影响,仍然正常输出[8],但检测轮编码器输出脉冲数将与正常行驶状态不同。
机器人转向时,定义逆时针方向为正方向。机器人转向的方式有2种:方式一,机器人以双轮检测结构的轴心为中心转向,左驱动轮与右驱动轮行驶速度完全相等;方式二,机器人以双轮检测结构轴线的延长线上的某点为中心转向,左驱动轮与右驱动轮行驶速度由转向与转向半径决定。
2 车轮打滑模型与辨识
机器人正常运行有4种状态:前进,后退,左转向,右转向[9]。机器人车轮打滑有3种状态:左驱动轮打滑,右驱动轮打滑,2个驱动轮均打滑[10]。中央控制器对打滑状态的判断顺序为:先判断是否存在左驱动轮打滑或右驱动轮打滑,再判断是否存在2个驱动轮都打滑[11]。
机器人运行时,每隔时间Δt,中央控制器计算车轮Y2与Y1的编码器输出脉冲数差值,其值为
ΔQ=Q2-Q1
(1)
式中Q1,Q2分别指车轮Y1,Y2的编码器输出脉冲数。
在直行和方式一转向状态,若ΔQ大于0,说明左驱动轮打滑,机器人出现向左偏转的运行方向误差;ΔQ小于0,说明右驱动轮打滑,机器人出现向右偏转的运行方向误差。
在方式二转向状态,机器人正常行驶,编码器输出的脉冲数满足
(2)
式中P1,P2分别指车轮X1,X2的编码器输出脉冲数,ΔQ由式(1)计算得出,R,R1,R2分别为车轮X1,Y1,Y2与车轮X2之间的距离。
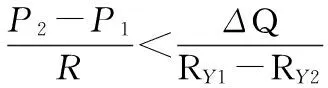
采用方式二转向时,机器人转向过程中因驱动轮打滑造成运行方向误差,记检测轮Y2在打滑过程中输出的误差脉冲数为X,X的计算表达为
(3)
若因驱动轮打滑,机器人出现向右偏转的运行方向误差,在直行、转向方式一和转向方式二状态,判断是否存在2个驱动轮都打滑的判定式分别为
(4)
(5)
(6)
式中 X由式(3)求出,R1,R2分别为车轮X1,Y1与车轴中点之间的距离。
若机器人运行时,由驱动轮打滑引起向右偏转的运行方向误差,判定式(4)、式(5)、式(6)成立,则机器人在直行、转向方式一和转向方式二状态,不存在2个驱动轮均打滑的状态。
根据判定式(4)、式(5)、式(6),可得到驱动轮打滑引起机器人运行方向向左偏转时,判断直行、转向方式一和转向方式二状态是否存在2个驱动轮都打滑的判定式。
3 方向误差计算与校正
机器人运行时,在t1,t2,t3,…,tn时刻,中央控制器根据车轮X1,X2,Y1,Y2的编码器输出脉冲数计算机器人的行驶误差,在每个采样周期,如果根据打滑模型,得出机器人存在运行方向误差,则机器人行驶误差计算表达式为
(7)
式中 ΔQk由式(1)求出。
根据式(7),可得机器人在运行过程中的累计误差为
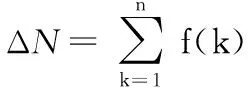
(8)
式中 f(k)由式(7)求出。
根据式(8),可得机器人运行过程中的累计修正误差为
(9)
机器人在直行和转向方式一,在2个驱动轮均打滑的模型中,不同的方向误差状态不同,机器人左驱动轮和右驱动轮在行驶方向的位移误差计算表达式为
(10)
机器人在转向方式二,2个驱动轮均打滑的模型中,不同的方向误差状态,左驱动轮位移误差计算表达式为
(11)
式中ΔNx2由式(12)求出。
机器人在转向方式二,2个驱动轮均打滑的模型中,不同的方向误差状态,右驱动轮位移误差计算表达式为
(12)
式中 ΔNx1由式(11)求出。
记误差校正阈值为Nd。若ΔN≥|Nd|,中央控制器控制驱动轮,对移动机器人的累计修正误差S进行校正。若机器人左右驱动轮在行驶方向的累计误差量均大于误差校正阈值Nd,则对该误差进行校正。
正向校正算法为:若机器人行驶的累计误差ΔN≥Nd,正向驱动左驱动轮X1,校正量为S;若累计误差ΔN≤(-Nd),正向驱动右驱动轮X2,校正量为S。正向校正算法分为2个阶段,第一阶段为校正方向误差;第二阶段为校正2个驱动轮均打滑引起的行驶方向位移误差。
反向校正算法为:若机器人行驶的累计误差ΔN≥Nd,反向驱动右驱动轮X2,校正量为S;若累计误差ΔN≤(-Nd),反向驱动左驱动轮X1,校正量为S。反向校正算法分为3个阶段:第1阶段为校正方向误差;第2阶段为校正行驶方向的位移误差;第3阶段为校正2个驱动轮均打滑引起的行驶方向位移误差。
4 仿真验证
4.1 仿真参数
主要参数如下:车轮半径r=3.5 cm;车轮每转1周编码器输出脉冲数i=900;车轮X1与X2之间的距离R=40 cm;车轮Y1与X2之间的距离RY2=30 cm;车轮Y2与X2之间的距离RY2=10 cm;采样周期Δt=0.2 s;误差校正阈值Nd=9;机器人在直线和转向方式一,左右驱动轮的行驶速度为22 cm/s;机器人在转向方式二,左右驱动轮的行驶速度根据转向半径设定。
4.2 仿真结果与分析
在Matlab环境下对机器人的运行与控制仿真,机器人总共运行14.4 s,对72个时间点的运行状态进行记录并分析计算。机器人运行过程中,在每个采样周期,每个车轮的编码器输出脉冲数如图2所示,(a),(b),(c),(d)分别为车轮X1,Y1,Y2,X2的编码器输出脉冲数。(a)与(d)中,正值表示驱动轮正向驱动,负值表示驱动轮反向驱动。

图2 车轮编码器输出脉冲数
对图2所示采样结果分析:图2中出现的误差,其来源主要有3个:1)编码器采样精度误差;2)驱动轮打滑;3)地面不平坦造成的非点源轮与地面接触。其中,由编码器采样精度引起的误差属于系统误差,本文按照打滑误差进行处理。
根据驱动轮X1,X2的编码器输出脉冲数,得出预设行驶轨迹,如图3所示。
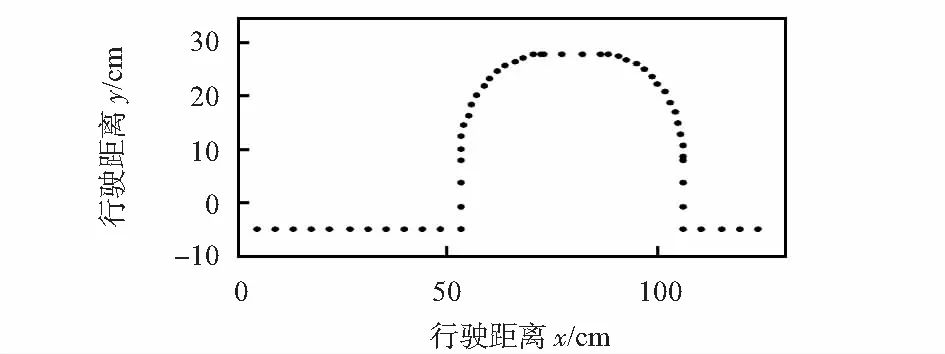
图3 预设行驶轨迹
对图3所示轨迹分析:机器人在2.4,11.8s时,通过转向方式一逆时针转向,转向角度为90°;在4.6,8.2s时,机器人通过转向式二顺时针转向,转向半径为20cm,转向角度为90°,左驱动轮行驶速度为22cm/s,右驱动轮行驶速度为0cm/s。
机器人运行过程中,如果对驱动轮打滑引起的运行方向误差不进行校正,根据图2所示的驱动轮X1,X2与检测轮Y1,Y2的编码器输出脉冲数,出未校正行驶轨迹,如图4所示。

图4 未校正行驶轨迹
将图3所示的预设行驶轨迹与图4所示的未校正行驶轨迹对比分析:机器人运行时,如果不对机器人驱动轮打滑引起的运行方向误差进行校正,机器人行驶轨迹将严重偏离预设行驶轨迹。
根据正向校正算法对驱动轮打滑引起的方向误差校正,校正后的行使轨迹,如图5所示。
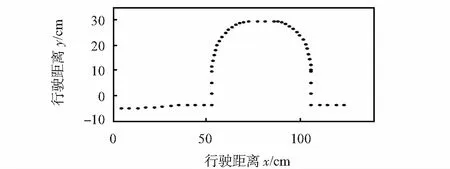
图5 正向校正行驶轨迹
将图3所示的预设行驶轨迹与图5所示的正向校正行驶轨迹对比分析:采用正向校正算法对方向误差校正后,产生了机器人移动中心偏移误差,但机器人行驶轨迹与预设行驶轨迹基本一致。经分析,若机器人左驱动轮打滑,则机器人移动中心偏移误差向左轮内侧偏移,若右驱动轮打滑,则机器人移动中心偏移误差向右轮内侧偏移,机器人移动中心偏移误差大小为
(13)
式中r为车轮半径,i为车轮每转一周编码器输出脉冲数。
根据反向校正算法对驱动轮打滑引起的方向误差校正,校正后的行使轨迹如图6所示。
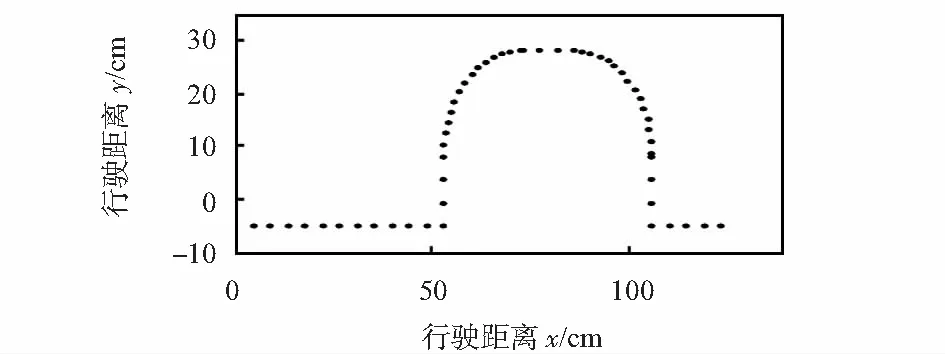
图6 反向校正轨迹
将图3所示的预设行驶轨迹与图6所示的反向校正行驶轨迹对比分析:采用反向校正算法对方向误差校正后,机器人行驶轨迹与预设行驶轨迹相比,存在的误差极小。误差产生的原因为:机器人运行时,累计误差ΔN未超出误差校正阈值Nd,系统不能对该误差进行校正,如果机器人在该状态下长时间运行,机器人移动中心会有一定的偏移误差。针对本文的仿真参数,如果机器人在累计误差ΔN=7的状态下运行20 s,移动中心的偏移误差为1.88 cm。
正向校正算法与反向校正算法相比,反向校正算法需要变换两次电机转向,从而对机器人运行误差进行校正,而正向校正算法无需调节电机转向,其校正逻辑比反向校正算法简单,能量消耗少,但是,从仿真结果分析,反向校正算法的校正精度优于正向校正算法。
5 结 论
利用该模型能够判断机器人在直行和不同转向方式下是否发生驱动轮打滑,实时计算方向误差量并校正。通过仿真证明:该系统能够对机器人长时间运行产生的打滑误差进行累计,自动辨识打滑模型并根据不同的校正算法进行误差校正,实现高精度的驱动轮打滑检测和路径跟踪控制。本文未能得出系统在实际复杂环境中运行的最佳误差校正阈值,使系统的鲁棒性达到最优,该问题留待以后做进一步研究。
[1] 高云峰,周 伦,吕明睿,等.自主移动机器人室内定位方法研究综述[J].传感器与微系统,2013,32(12):1-5.
[2] Borenstein J,Feng L,Wehe P D K,et al.UMBmark—A method for measuring,comparing,and correcting dead-reckoning errors in mobile robots[M].Ann Arbor,USA:University of Michigan,1994.
[3] Endo D,Okada Y,Nagatani K,et al.Path following control for tracked vehicles based on slip-compensating odometry[C]∥2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS 2007,IEEE,2007:2871-2876.
[4] Ibraheem M.Gyroscope-enhanced dead reckoning localization system for an intelligent walker[C]∥International Conference on Information,Networking and Automation,2010:67-72.
[5] Cho B S,Moon W S,Seo W J,et al.A dead reckoning localization system for mobile robots using inertial sensors and wheel revolution encoding[J].Journal of Mechanical Science & Technology,2011,25(11):2907-2917.
[6] 王真星.嵌入式产品分析与设计[M].北京:电子工业出版社,2013.
[7] 胡 桐.四轮独立驱动和转向移动机器人的设计与控制[D].合肥:合肥工业大学,2015.
[8] Nagatani K,Endo D,Yoshida K.Improvement of The odometry accuracy of a crawler vehicle with consideration of slippage[C]∥2007 IEEE International Conference on Robotics and Automation,2007:2752-2757.
[9] 吴 耀,王田苗,王晓刚,等.基于自适应卡尔曼滤波的侧滑移动机器人运动模型估计[J].电子与信息学报,2015,37(12):3016-3024.
[10] 王卫华,熊有伦,孙容磊.一种移动机器人轮子打滑的实验校核方法[J].机器人,2005,27(3):197-202.
[11] 李泉溪,赵帅鹏,武文琪.扫地机器人车轮打滑检测与修正研究[J].制造业自动化,2015,37(11):12-18.
Method for detecting and checking wheel slipping of mobile robot*
ZHAO Shuai-peng, LI Quan-xi , XUE Xiao, SHEN Fang
(College of Computer Science and Technology,Henan Polytechnic University,Jiaozuo 454003,China)
Aiming at non-system error caused by wheel slipping of mobile robot,propose double wheel detection structure model.Based on number of output pulses of encoder of driving wheel and testing wheel,the wheel slipping model for straight line and different steering mode is established and the slipping identification algorithm are given.The operation direction error and displacement error are corrected by the forward correction algorithm or the reverse correction algorithm.The simulation results show that the structure model can be used to accumulate the slipping errors caused by long time operation of the robot,and real-time correction.There is little displacement error in the reverse correction algorithm.The correction precision is superior to the forward correction algorithm,but the forward correction algorithm is simple,and the energy consumption is low.
double wheel detection structure; slipping model; forward correction; reverse correction
10.13873/J.1000—9787(2017)05—0059—04
2016—05—10
国家自然科学基金资助项目(61175066,60905041);河南省高校科技创新人才资助项目(2012HASTIT013);河南省高校重点科研项目应用研究计划资助项目(2011GGJS—056)
TP 301
A
1000—9787(2017)05—0059—04
赵帅鹏(1990-),男,硕士研究生,主要研究方向为嵌入式系统、计算机控制技术。
