基于卤键的谢尔宾斯基三角分形自组装的模拟研究

张珍 谢文俊,2 杨奕 孙耿 高毅勤,2,*

(1北京大学化学与分子工程学院，理论与计算化学研究所，北京分子科学国家实验室，北京100871；2北京大学，生物动态成像中心，北京100871)

基于卤键的谢尔宾斯基三角分形自组装的模拟研究

张珍1谢文俊1,2杨奕1孙耿1高毅勤1,2,*

(1北京大学化学与分子工程学院，理论与计算化学研究所，北京分子科学国家实验室，北京100871；2北京大学，生物动态成像中心，北京100871)

采用粗粒化的格点模型和蒙特卡罗方法，对在三角网格表面通过自组装形成了谢尔宾斯基三角分形结构进行了模拟研究。研究发现，对称和非对称基元都可以自发形成谢尔宾斯基三角分形结构，然而对于非对称分子的对映异构体的混合物，由于大量的具有竞争性的三元节点的出现，很难形成更高阶的分形结构。我们还发现，分形结构在表面覆盖度低的时候才会出现，而且对温度较为敏感。此外，为了检测是否可以通过分子设计来控制组装途径和结果，我们通过使用与组装基元不同的模板来实现对自组装过程和结果的控制。其中，模板作为“催组剂”诱导自组装，但不会出现在最终的组装结构中。

自组装；蒙特卡罗模拟；分形；谢尔宾斯基三角形；催组装

1 In troduc tion

Molecular self-assembly on 2D surfaces has gained extensive attention for its practical applications in material science and nanotechnology1－4.Myriad functionalmolecular architectures,including porous networks2,5,6,compact periodic patterns7,chiral assemblies7－9and glassy overlayers10,11,have been reported toform spontaneously on various surfaces.Within these architectures, fractals like Sierpiński triangle(ST)which exhibita self-similar pattern at different scales are of special importance in mathematics,engineering and science12.Synthesisofmolecular fractals relies mainly on the coordination between metal atoms and organic ligands.Such studies include bis-terpyridinebuilding blocks which can be co-adsorbed w ith Ru and Fe atoms toform a nanometer-scale Sierpiński hexagon gasket13.Multitopic terpyridine ligands can form hexagonw reath structuresof fractal featureswith Zn(II)ions14.Certain organicmolecules containing two carbonitrile groupswere alsofound to be coordinated with Ni atoms toform ST fractalsof high thermalstability15.Apart from the above coordinationmediated molecular fractal formation,Wu etal.16reported recently the self-assembly ofmolecular building blocks into defect-freemolecular ST fractals through halogen bonds.

Complementary to experiments,computational studies have made important contributions to our understanding of the formationmechanism ofmolecular fractals.For example,theMonte Carlo(MC)methodwassuccessfully used to predictplausibleselfassembling STs using simplemodel systems.Using MC simulation,Niecharz and Szabelski17proposed thatmolecular fractals can be formed by coordination bonds.They alsofound thatbent molecular building blocks,equippedw ith two identicalelectron donor centers as linkers,can form ST fractalpatternswithmetal centers18.Recently,the self-assembly of hydrogen-bonded STswas reported19.In their study,symmetric linkermoleculeswere used to create STs.

In this paper,we simulate the formation of ST fractals using both symmetric and asymmetricmolecules.The coarse-grained molecularmodelused in canonical lattice MC is inspired by the molecular design ofWu etal.16.We compare the difference between symmetric and asymmetricmolecular building blocks in this spontaneous process,which has not been analyzed from a computational aspect before.We find that the simple coarsegrained model can effectively reproduce the ST fractals observed experimentally forboth symmetricaland asymmetricalmolecules. The simulations suggest that it ismore difficult toform large fractals for them ixture of enantiomersof asymmetricmolecules than for symmetricmolecules,ofwhich theunderlyingmolecular mechanism is revealed and possible roles of themetal lattice is discussed.Them ixed system can form a large variety of nodal motifs.Specifically,themixture of enantiomers can self-organize into different formsof distorted triangular-shaped structures.The existence of the various nodal motifs reduces the formation probability of the fractal self-assembly w ith a uniform chirality. In addition,we devised a template to induce themolecular organization of asymmetric building blocks into a pre-designed pattern instead of the spontaneously formed ST fractal pattern.We used such a controlled pattern formation to show the feasibility of catassembly in which thedevised templateactsascatassembler20,21.

2 Models and m ethods

To simulate the self-assembly ofmolecules into ST fractals,we used a coarse-grainedmolecularmodel shown schematically in Fig.1.Themodelwas inspired by the recentexperimentswhich demonstrated the self-assembly of aromatic bromo compounds including 4,4″-dibromo-1,1′:3′,1″-terphenyl(B3BP)and 4,4′′′-dibromo-1,1′:3′,1″:4″,1′′′-quaterphenyl(B4BP)into Sierpiński triangles on Ag(111)surface16.The three-fold halogen bonding plays an important role in the formation of the defect-free hierarchical fractalstructure.For simplicity,wemodel themolecular building blockswith rigid planes.A and B shown in Fig.1 are the modelsused formolecules B3BPand B4BP,respectively.Due to the asymmetry of B4BP,molecule B forms two enantiomeric surface-bound structures,BLand BR.In the simulated systems,the molecules are confined to a2D rhombic fragmentof a triangular lattice which represents the Ag(111)surface with each vertex serving as an adsorption site,and each phenyl ring of B3BP or B4BPis coarse-grained as one segmentoccupying oneadsorption site.

In this simplified approach,themolecules are allowed to interact through triangular halogen bonds.Once the triangular halogen bond is formed,thenucleophile positive region of one Br atom points to the equatorial electrophile region of an adjacentBr atom,with each Bratom actingasboth adonorand anacceptor22,23. Ithas been reported that this triangular halogen bond plays a key role in many self-assembled molecular networks that involve halogen atoms24,25.We should note here that different types of angular preferences for halogen－halogen interactions havealso been observed26,27.

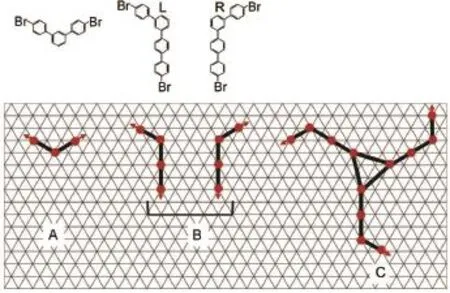
Fig.1 Chem icalstructuresof the B3BPand B4BPmoleculesTheir schematic counterpartsare used in the simu lation on a triangulargrid.The red arrowson the term inalofm olecules indicate the direction of C―Br covalent bond.Twomirror-imagesofmolecule B aremarked by L and Rwhen adsorbed on thegrid.C representsan exampleofawindmill-likemoleculewith threemembered armsadsorbed on a triangular lattice.coloronline

Fig.2 show s the coordination nodalmotifs that are allowed in the simulations.The possiblenodalmotifsofmolecules A and B which can be formed in theoverlayerhavebeen listed in Figs.S1－S5(Supporting Information(SI)).Thehalogen bond interaction between a term inal segment of onemolecule w ith another is characterized by the parameterεa=－1.Moreover,it is importantto note that steric hindering effects can strongly impact the formation of fractalpatterns.To take into accountsuch an effect,the nearest adsorption sites around onemolecule exclude the occupation of any othermolecules.When a segmentof onemolecule lies in the nextnearestadsorption site of anothermolecule,a repulsive interactionεrarises(e.g.,εr=0.5 is used in the current model).For simplicity,the interactionsbetweenmoleculesand the lattice substrate are not treated exp licitly in this currentmodel.

The MC simulationswere performed using the conventional canonical ensemble28,which is characterized by the number of molecules,the volume(substrate area),and the temperature.The substrate ism im icked as a rhombic fragment of a triangular grid of equivalent adsorption sites.We adopted periodic boundary conditions in the plane to eliminate theboundary effect.

The simulation procedure is as follow s.In the first step,N moleculesare random ly distributed on thegrid surface.Next,one of themolecules is random ly selected and its potential interaction energy in an initial configuration(Uold)is calculated.The associated interaction energy includes the attractive halogen bond interaction and the repulsive steric repulsion.Once Uoldis calculated,an attempt to move a selected molecule to a random ly chosen new position a cluster of adsorption sitesmatching the shape of themolecule was chosen random ly.If the selected adsorption sites are unoccupied,the potential energy of this new configuration(Unew)is then calculated.Since the sampling of molecular orientationsusing standard MC is very inefficient,we make use of the orientational bias sampling28.For the planar molecules considered here,six possible orientations can exist when they adsorb on the surface:when the coreof amolecule is pinned to the lattice,there are six different configurations rotating in the planew ith a rotation angleof 60 degrees.In the updating scheme,all these six configurationsare included in the calculation. To evaluate the acceptance probability,we calculate the Rosenbluth factor w()n for thenew configuration using

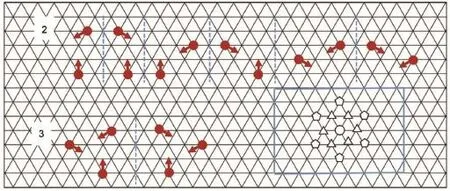
Fig.2 Halogen-bondingm otifs com prising 2 or 3m olecules during the sim ulation(only one term inal segm ent of amolecule is shown)The dashed b lue linewasused to separate two types of halogen-bondingmotifs.The triang les and pentagons correspond to the nearestand the nex tnearestadsorption sites,respectively.coloron line

where kBis the Boltzmann constant,T is the temperature of the system,and ujdenotes theenergy of j th trial configurations.Next, we choose one of the six trial configurations,say,x with a probability

and for theold configuration,the Rosenbluth factor w(o)isalso calculated using Eq.(1).To decidewhether themove is successful, theacceptance probability pacciscomparedwith a random number r∈(0,1)

If r＜pacc,themolecule ismoved to the new position.Otherw ise it remains at its originalposition.During oneMC step theabove procedure is repeated N times.

To explore catassembly,we additionally used conventional grand canonical MC(GCMC)28simulationmethod on a L×L triangular lattice at a tem perature of T.More specifically,the simulation procedure is described as follows.At the firststageof simulation,the substrate is solely occupied by w indm ill-shaped molecules(Fig.1C)which comprisea2Dmolecular network.The system is then equilibrated by successiveof three typesof trials includingmovement,deletion,and creation ofmolecules on the surface.Onceamolecule is randomly selected,an attempt ismade tomoveor to delete.We calculate theenergy for a configuration x by

where n takes a valueof 1 or3,depending the typeofmolecule, m is 2 or3,depending on interaction sitesofmolecule,εris the repulsive interaction,ariseswhen the next nearest adsorption site of onemolecule isoccupied by anothermolecule.εklisεa,εaw,or εwwdepending on whether thehalogen bond is formed by two BL, a BLand aw indm ill-likemolecule,or two windm ill-likemolecules,respectively.εsubis the interaction between themoleculeand the substrate.Tomove amolecule,w e adopt the same procedure as in the biased MC.To create amolecule,4n adsorption sites matching the shapeof themolecule are random ly chosen.If none of the selected sites areoccupied theadsorption of amolecule is attempted with a probabilityminu(Ni)]}],where Piis the partialpressure of the two components and Niis the number(density)of them.When the selected molecule attempts to desorb,it is attempted with a probability miSince the system is a multi-com ponent one,adsorption and desorption attem pts are performed for each kind ofmolecule under a specified partial pressure.With the increase of the pressure,the coverage of adsorbedmoleculeson the surface increases.So the pressuresof BLand windm ill-like molecules used here are P1=10－10and P2=10－8,respectively.The interaction strengths areεa=－1.6 andεww=－1.0,supplemented by the Lorentz-Berthelotm ixing rules as geometric average for the interaction between BLand windmill-likemolecules,andεr=0.5.Since the overall interaction ofw indmill-likemoleculeswith the substrate is stronger than theBLmolecules,the interacting strengthsof BLandwindmilllikemolecules w ith the substrate are taken as 0 and－1.4,respectively.

In the simulations,typically up to 108MC stepswere taken.The simulationswere performed on a L×L(L=300)triangulargrid and the totalnumber ofmolecules is N=800.For simp licity,kBand T areassumed to be dimensionlessparameters,kB=1 and T= 0.2 if nototherw ise stated.

In addition,density functional theory(DFT)calculationswere used to provide an estimate of the interaction energies in the coarse-grained MC modeling.The effect of substrate was not considered here.All the DFT calculationswere carried outby CP2K program29,30w ith a hybrid Gaussian and p lane waves approaches.During all the calculations,the energy cutoff for the planew aves is setas320 Ry and the convergence criteriaof selfconsistent field(SCF)method during the wavefunction optimization is set as 5.0×10－7.The exchange-correlation energy of electrons is calculated by generalized gradient approximation (GGA)function of Perdew-Burke-Ernzerh31.Themolecularly optimized double zeta-polarization(DZP)basis functionsareused for allatoms32.During the structureoptimizations,themolecules arecentered in avery largeboxwith dimensionsof 50 nm×50 nm× 20 nm and no constraints are applied.The optim izations are stopped until themax componentof forces is smaller than 0.03 eV·nm－1.

3 Resu lts and discussion

3.1 Sim u lations usingm o lecu les A or BL

We firstperformedMC simulations foraone-componentsystem composed of 800molecule A,ofwhich the simulated results can be directly compared with the experimental observations in Ref.16.Fig.3 depicts a typical snapshot of the self-assembled system.ST fractalstructuresofdifferentorders canbe clearly seen from this figure.The self-assembled fractal structure shown in Fig.3b agrees w ith that observed in experiment for B3BP on Ag(111)16showing thatour simple coarse-grainedmodel can serve asa reasonable representation of the experimental system.In this structure,each node comprisesof threemolecularbuilding blocks that form either a clockwise(CW)or counterclockw ise(CCW) pattern asshown in themagnified fragment(Fig.3b,Fig.3b′).The nodes in one fractal havea unique rotationalmode and they are motifs of a uniform chirality.The twofractal patternswhich are mirror-images to each otherare formedwith an equalprobability.

The ST fractals formed bymolecule A can beof differentorders.Such a high dispersity in formation order does notdecrease with the further increaseof the simulation time,showing that it is difficult formolecule A toform big ST fractals.This phenomenon can be readily explained as follows.The fractals grow through the attachmentofmolecule A to oneof the threeaccessible vertices of the ST fractals,the number of which remains constantas the perimeterof theassembled structure increases.Such an effectwas also seen in the ST fractals formed by simulated annealing of the symmetric linker andmetalatoms18.These results highlight the interesting difference between fractal formation and crystal grow th.In the latter,the Ostwald ripeningmechanism leads to the formation of a large crystal and the disappearanceof smallerones. One can thus conclude that the shapeof thebuilding block and the triangulararrangementofmolecularbonding areessential for the ST fractal formation.

Fig.3 A typicalpattern of thesystem consisting 800moleculeATheblue arrowsdenote the two typesof rotation of the three-fold bonding:CCW(left)and CW(right).Magnified fragments(a－c)respectively represent the first, thesecond and the third order of the ST.Themagnified fragment(b′)is theenantiomerof(b).color online

Next,we investigated the self-assembly of asymmetric building blocks BL(Fig.1).A typical snapshotof the adsorbed overlayercomprising 800moleculesof BLand containing two typesof nonenantiomorphous STs is shown in Fig.4.This simulation outcome is different from molecule A.The primary reason for their difference lies in theasymmetric featureof thebuilding block BL.For convenience,the pore of the ST formed through threemolecules in Fig.4eand Fig.4e′arenamed typeαandβ,respectively.Type βbutnot typeαappears to be a regular hexagon.The formation of the ordered fractalpatterns ismainly a resultof the entropic stabilization of nodesof type a(heterotactic nodes)which have a formation probability three times higher than nodes of type b (w indm ill nodes).On the other hand,the grow th of imperfect fractal patterns ismainly resulted from the formation of the windm illnode.

We nextexplored the effectof surface coverage and tem peratureon themorphology of theadsorption layer.In Fig.S6(Supporting Information),we show thatatahigh surface coverage the molecules of BLtend toform large triangular aggregatesw ith a diversifiedmorphology.Athigh temperatures,clusters only form transiently and remain small in size(Fig.S7,Supporting Information).In contrast,at low temperatures the system is easily trapped to configurations consisting of a large variety of irregular structures.Only at proper temperatures can themolecules BLaggregate toform stable fractalpatterns.We further analyzed the effectof temperature on the nodes of differentpatterns,including two-fold,heterotactic,andwindmill-likehalogen-bonding nodes. The number of thesenodes atdifferent temperatureswere shown in Fig.S8.Itwas found that thenumber of heterotactic node increasesw ith the decreasing of temperature.When the overlayer is sufficiently cooled,say,T<～0.25,the system prefers heterotactic nodes and the number of w indmill-like nodes is much smaller.A sim ilar temperature dependence was previously observed for theself-assembly of STs inmetal-organic and hydrogenbonded systems18,19.Configurationswith typeαandβpores are both observed in the simulation.Tofurther illustrate their differences,we used DFT to calculate the energy of themolecular configurations consisting of the two typesof pores(Fig.S9(a)and Fig.S9(b),Supporting Information).Themolecular configuration containing typeαpore is lower in energy than thatof a typeβpore by～2.5 kJ·mol－1(see Fig.S9).This difference between these molecular configurations is taken into account in terms of an additionalenergy penalty(an energy of 1.5 energy unit)for the typeβpore.Asshown in Fig.5,when such an effect is considered, only one typeof stable fractal pattern is formed in the simulation.

3.2 Sim u lations using them ixture ofm o lecu les BLand BR

In experiments,when prochiralmolecules adsorb on a solid surface,a racemic overlayer composed of equalamountsof both surface enantiomers is expected.Fig.6 demonstrates the results obtained for the simulationwith 800moleculesof BLand BR(with a ratio of 3:1)at the temperature T=0.125.The reason for choosing this ratio of BLand BRis that the smallestcycleobserved in experiments is consisted of the same typeof 3molecules BLor BR:if BLforms the cycle,the linker is then BRand vice versa.As observed in the experiment16,the firstgeneration of ST is composed of 9moleculesof BLand 3moleculesof BR.We should note that the realsystem should contain racemicmixtures,namely,with equal populations of BLand BRon the solid surface.The observation of the 3:1 structure in the presence of racem icm ixtures indicates the possible roleof thematching between the latticeand adsorbates in determining the fractal structures.Such an effect should be considered by including explicitly the solid lattice but isnot included in the simplemodelsused in thisstudy.

Tofurther distinguish between the different structural units observed in the simulations,weagain used DFT to calculate theenergy of the configuration in Fig.S9c,which includes onemolecule BLand twomolecules BR.Itwas found that this configuration hasa higher energy than the configuration of typeαby～1.3 kJ·mol－1(see Fig.S9).This configuration was in factonly observed for the simulation,but not in the experiment.To incorporate such information,in the following simulationwe added an energy penalty(again,a valueof 1.5wasused)for configurations composed of both BLand BR.

Fig.5 A typical pattern of the system com posing 800molecu les BLinwhich the interaction ofbond w ith CW chirality isweaker

Fig.6a showsa fractalstructure inwhich every node consistsof mixed enantiomersof B.Theoverall fractalpattern is formed of nodeswith aunique chirality(theenantiomorph isnotshown here, a structure representing the oneobserved in the experimentusing B4BP16.Such an agreement show s that the simplemodelused in this study is capable of reproducing fractal structures observed experimentally for both symmetric and asymmetric building blocks.The formation of a variety of triangular-shaped structures are also shown in Fig.6.The structural diversity of theseaggregates is a result of the variance in the coordination nodes.In addition,we also examined the self-assembly of overlayers containing both conformersofmolecule B with racemic composition. The first-order of the ST is observed as can be seen in Fig.S10 (Supporting Information).The magnified fragment shows the fractal structurew ith one type of handednessw ith the ratio of BLand BRas 1:3.We failed to observe large and regular fractal structures in racem icmixture.

3.3 Designing se lf-assem b ly patterns

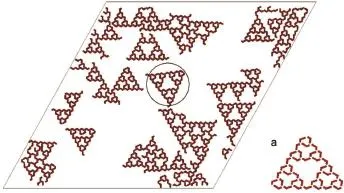
Fig.6 A typicalpattern of the system com posing of 800moleculesof BLand BR(3:1)Themagnified fragmentshows thestructurew ith different molecular typesbetween bridgeand ring.

The simulations discussed above showed that the building blocksBLdesigned here can spontaneously form ST through selfassembly,but not the porous network shown in Fig.S11(Supporting Information).This preference of structure formation is expected from a thermodynam ic point of view.Let′s take the porous network(Fig.7a)and the second generation of ST fractal (Fig.7b)formed by 12moleculesas examples,which are denoted by state A and state B,respectively.The free energy differenceof the two states can be estimated throughΔF=EA－kBT ln(m)－(EB－kBT ln(n)),w here EAis the interaction energy of state A,EBis the interaction energy of state B,T is the temperature,m and n are the total number of configurations that is accessible to the system atenergies EAand EB,respectively.The freeenergy of the porousnetwork(Fig.7a)isabout－18.62,while thisvalue for the fractal structure(Fig.7b)is－21.14,show ing that the building blocksof the fractalstructureare indeed thermodynamicallymore stable.Wegave detailed information on the calculation in SI.On theother hand,one should note thatheterotatic andwindmill-like nodes are energetically equivalent.This preference of structure formation originatesmainly from the entropic stabilization of the heterotactic nodeswith the ratio of heterotactic andwindmill-like nodesas3:1.Asmentioned above,thenumberof thewindm illlike nodes increases with T,ismuch smaller compared to heterotactic nodes.While thewindmill-likenodesare responsible for the formation of the porous network as shown in Fig.S11.The porous network is impossible to be observed in this system although the temperature is low.

Fig.7 Schematic diagram sof two typesof self-assembly structures com posed of 12moleculesBL

Therefore,the preference of fractal structures over the porousones leads toan interestingquestion:isitpossible toguide theselfassembly into theporousnetwork structurebymaking use the idea of catassembly20,21?In catassembly,catassemblerareadded into the system to alter the kineticsof an assembly process.Catasemblers do notappear in the final structure and thus do not change the overall thermodynam ics but can either change the rate of selfassembling or lead to varied kinetically controlled products. Following this concept,we propose the following strategy.Firstly, catassemblers that can form the desired target structure are introduced into the system.Theadsorption of catassembler initiates biased self-assembly.Next,the assemblers displace the catassembler through adsorption to the surface,e.g.,asa resultof the favored interaction among them selves.The success of such a design requires the critical nuclear size to be small for the catassembler and at the same time the assemblers form a thermodynamically more stable structure which excludes the catassembler.To achieve such agoal,we designed catassemblers that have a largermolecular size butaweaker interacting strength than theassemblers.Once theassemblers adsorb,catassemblers are to be gradually excluded from the surface.Asa result,assemblers aggregate and self-organize into a structureguided by the catassemblers instead of the spontaneously formed one.It should be pointed out that the template used here is different from those used in template-assisted self-assembly.In template-assisted self-assembly,templates remain in the finalstructureasbuilding blocks. In contrast,the catassemblers do notappear in the finalself-assembled structure.

Fig.8 Four typicalsnapshotsof the structureof the adsorbed phase corresponding to differentMC stepsduring oneMC simulationThemolecules represented in red and blue corresponding to BLmolecule,w indmill-likemolecule,respectively.color online

On the basisof the above idea,we proposed a MCmodelusing windmill-shaped catassemblers(Fig.1C)and BL(Fig.1B).These catassemblershave the same adsorption sitesas thew indm ill node formed by three BLmoleculeswhich can further self-organize into highly ordered porousnetworks(Fig.8).

We performed calculations using the GCMC simulation method.Fig.8 shows four snapshotswithin oneMC simulation. Asseen from Fig.8(t=0),theordered porousnetwork is initially a template composed ofwindm ill-like catassemblermolecules. Compared to catassemblers,BLmolecules interactwith each other more strongly on the surface and thusonce a nucleus is formed by the catassemblers,it iseasy for BLto adsorb to and remain in the structure.Fig.8(t=9.5×105MC steps and t=2.05×107MC steps)shows thata process inwhich the self-assembled structure propagates through adsorption,desorption andmovementof BL, dictated by the initial structure formed by the catassemblers.In this process,the windm ill nodes formed by threemolecules BLinsert into thegap formed by self-assembled catassemblers,followed by the detachmentof a catassembler nearest to thew indmill nodes from the surface.Theadsorption of a BLto the vacated sites deprives the catassembler from re-adsorbing.The insertion of two othermolecules BLinto the unoccupied space leads to the formation of a new w indmillnode.In thismanner,the porous network com posed of molecules BLcontinuously grow s.Furthermore,due to the steric hindrance of windm ill-likemolecules, molecules BLare prevented from the spontaneous formation into ST structures and the assemblers assemble into a large ordered porous network.In the simulations,wealso observed that faulted connections between BLmolecules exist in the porous network which are subsequently amended.

4 Conc lusions

In summary,we have demonstrated the formation of highlyordered fractal structuresw ith a specific chirality when simple latticemodels are used in simulations.Density functional theory calculationswereused to evaluate the relative stability of various unit structures formed in the self-assembly of asymmetric molecule.We observed that both symmetric and asymmetric building blocks can self-assemble into ST.Itwas found that the ST tends toform at low surface coverage,and only in a lim ited temperature range.The simulations on themixtures of the enantiomers of asymmetric molecules showed that the increased number of possible coordination nodes can lead to the formation of the perturbed triangular-shaped structure.It is more difficult for asymmetricmolecules to self-organize into ST with a uniform chirality than the symmetric ones.In addition,we reported a conceptual strategy for changing the self-assembly processof BLfrom ST fractal structure to a disfavored structure.Important factorssuch as specific surface structures,latticematching,and interactionspotentially support the formation of thehigherorder of ST fractal structure.However,the current simulation uses highly simplifiedmodelswhich do not take into account the detailed interactions betw een the solid lattice and the adsorbates. Atom ic detailedmodelsareneeded to include such effects.

Acknow ledgm ents:We thank Peking University for providing the computational resources.

Supporting In formation:Possible nodalmotifs ofmolecule A andmolecule Bwhich can be formed in the overlayer have been listed.The snapshots of the adsorbed overlayer under different temperature and high surface coveragewere shown.Thenumber of two-fold,heterotatic,andwindmill-likehalogen-bonding nodes at different temperature were descripted.The energy of themolecular configuration consisting of the three types of poresw as calculated by density functional theory.Estimation of the free energies of the porous network and the fractal structure were given.This information isavailable free of charge via the internet athttp://www.whxb.pku.edu.cn.

(1)Stepanow,S.;Lingenfelder,M.;Dmitriev,A.;Spillmann,H.; Delvigne,E.;Lin,N.;Deng,X.;Cai,C.;Barth,J.V.;Kern,K. Nat.Mater.2004,3,229.doi:10.1038/nmat1088

(2)Zhang,R.;Wang,L.C.;Li,M.;Zhang,X.M.;Li,Y.B.;Shen, Y.T.;Zheng,Q.Y.;Zeng,Q.D.;Wang,C.Nanoscale 2001,3, 3755.doi:10.1039/c1nr10387c.

(3)Ivasenko,O.;MacLeod,J.M.;Chernichenko,K.Y.;Balenkova, E.S.;Shpanchenko,R.V.;Nenajdenko,V.G.;Rosei,F.; Perepichka,D.F.Chem.Commun.2009,1192.doi:10.1039/ B819532C

(4)Theobald,J.A.;Oxtoby,N.S.;Phillips,M.A.;Champness,N. R.;Beton,P.H.Nature 2003,424,1029.doi:10.1038/ nature01915

(5)Kudernac,T.;Lei,S.;Elemans,J.A.A.W.;De Feyter,S.Chem. Soc.Rev.2009,38,402.doi:10.1039/B708902N

(6)Furukawa,S.;U ji-i,H.;Tahara,K.;Ichikawa,T.;Sonoda,M.; De Schryver,F.C.;Tobe,Y.;De Feyter,S.J.Am.Chem.Soc. 2006,128,3502.doi:10.1021/ja0583362

(7)De Feyter,S.;De Schryver,F.C.Chem.Soc.Rev.2003,32,139. doi:10.1039/B206566P

(8)Lei,S.;Tahara,K.;Müllen,K.;Szabelski,P.;Tobe,Y.;De Feyter,S.ACSNano 2011,5,4145.doi:10.1021/nn200874k

(10)Blunt,M.O.;Russell,J.C.;Giménez-López,M.D.C.; Garrahan,J.P.;Lin,X.;Schröder,M.;Champness,N.R.;Beton, P.H.Science2008,322,1077.doi:10.1126/science.1163338

(11)Tahara,K.;Furukawa,S.;U ji-i,H.;Uchino,T.;Ichikawa,T.; Zhang,J.;Mamdouh,W.;Sonoda,M.;De Schryver,F.C.;De Feyter,S.;Tobe,Y.J.Am.Chem.Soc.2006,128,16613. doi:10.1021/ja0655441

(12)Mandelbrot,B.B.The FractalGrometry ofNature;W.H. Freeman and Company:San Francisco,1982.

(13)Newkome,G.R.;Wang,P.;Moorefield,C.N.;Cho,T.J.; M ohapatra,P.P.;Li,S.;Hwang,S.H.;Lukoyanova,O.; Echegoyen,L.;Palagallo,J.A.;Iancu,V.;Hla,S.W.Science 2006,312,1782.doi:10.1126/science.1125894

(14)Wang,M.;Wang,C.;Hao,X.Q.;Liu,J.;Li,X.;Xu,C.;Lopez, A.;Sun,L.;Song,M.P.;Yang,H.B.;Li,X.J.Am.Chem.Soc. 2014,136,6664.doi:10.1021/ja501417g

(15)Sun,Q.;Cai,L.;Ma,H.;Yuan,C.;Xu,W.Chem.Commun. 2015,51,14164.doi:10.1039/C5CC05554G

(16)Shang,J.;Wang,Y.;Chen,M.;Dai,J.;Zhou,X.;Kuttner,J.; Hilt,G.;Shao,X.;Gottfried,J.M.;Wu,K.Nat.Chem.2015,7, 389.doi:10.1038/nchem.2211

(17)Nieckarz,D.;Szabelski,P.J.Phys.Chem.C 2013,117,11229. doi:10.1021/jp4022486

(18)Nieckarz,D.;Szabelski,P.Chem.Commun.2014,50,6843. doi:10.1039/C4CC01344A

(19)Zhang,X.;Li,N.;Gu,G.C.;Wang,H.;Nieckarz,D.;Szabelski, P.;He,Y.;Wang,Y.;Xie,C.;Shen,Z.Y.;Lü,J.T.;Tang,H.; Peng,L.M.;Hou,S.M.;Wu,K.;Wang,Y.F.ACSNano 2015, 9,11909.doi:10.1021/acsnano.5b04427

(20)Wang,Y.;Lin,H.X.;Chen,L.;Ding,S.Y.;Lei,Z.C.;Liu,D. Y.;Cao,X.Y.;Liang,H.J.;Jiang,Y.B.;Tian,Z.Q.Chem.Soc. Rev.2014,43,399.doi:10.1039/C3CS60212E

(21)Wang,Y.;Lin,H.X.;Ding,S.Y.;Liu,D.Y.;Chen,L.;Lei,Z. C.;Fan,F.R.;Tian,Z.Q.Sci.Sin.Chim.2012,42,525.[王宇,林海昕,丁松园,刘德宇,陈亮,雷志超,范凤茹,田中群.中国科学:化学,2012,42,525.]doi:10.1360/032011-828

(22)Lu,Y.;Zou,J.;Wang,H.;Yu,Q.;Zhang,H.;Jiang,Y.J.Phys. Chem.A 2005,109,11956.doi:10.1021/jp0547360

(23)Cavallo,G.;Metrangolo,P.;M ilani,R.;Pilati,T.;Priimagi,A.; Resnati,G.;Terraneo,G.Chem.Rev.2016,116,2478. doi:10.1021/acs.chem rev.5b00484

(24)Walch,H.;Gutzler,R.;Sirtl,T.;Eder,G.;Lackinger,M.T. J.Phys.Chem.C 2010,114,12604.doi:10.1021/jp102704q

(25)Chung,K.H.;Park,J.;Kim,K.Y.;Yoon,J.K.;Kim,H.;Han, S.;Kahng,S.J.Chem.Commun.2011,47,11492.doi:10.1039/ C1CC14679C

(26)Desiraju,G.R.;Parthasarathy,R.J.Am.Chem.Soc.1989,111, 8725.doi:10.1021/ja00205a027

(27)Pedireddi,V.R.;Reddy,D.S.;Goud,B.S.;Craig,D.C.;Rae, A.D.;Desiraju,G.R.J.Chem.Soc.Perkin Trans.1994,2, 2353.doi:10.1039/P29940002353

(28)Frenkel,D.;Sm it,B.Understanding Molecular Simulation From Algorithm to Applications;Academic Press:London,2002.

(29)VandeVondele,J.;K rack,M.;Mohamed,F.;Parrinello,M.; Chassaing,T.;Hutter,J.Comp.Phys.Comm.2005,167,103. doi:10.1016/j.cpc.2004.12.014

(30)Ferrario,M.;Ciccotti,G.;Binder,K.ComputerSimulationsin Condensed Matter Systems:From Materials to Chemical Biology;Springer:Berlin Heidelberg,2006;Vol.1,pp 287－314.

(31)Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996, 77,3865.doi:10.1103/PhysRevLett.77.3865

(32)VandeVondele,J.;Hutter,J.J.Chem.Phys.2007,127,114105. doi:10.1063/1.2770708

Simulation Studies of the Self-Assembly of Halogen-Bonded Sierpiński Triangle Fractals

ZHANG Zhen1XIEWen-Jun1,2YANG Yi Isaac1SUNGeng1GAO Yi-Qin1,2,*
(1Institute ofTheoreticaland ComputationalChemistry,College ofChemistry and Molecular Engineering, Beijing National Laboratory ofMolecular Sciences,Peking University,Beijing 100871,P.R.China;2Biodynamic Optical Center,Peking University,Beijing 100871,P.R.China)

In this study,a coarse-grained lattice Monte Carlo mode lwas used to investigate the formation of Sierpińskitriangle(ST)fracta ls through self-assembly on a triangu lar lattice surface.In the simulations,both symmetric and asymmetricmo lecularbuilding blocks can spontaneously form ST fractalpatterns,although the m ixture ofenantiomers ofasymmetricmolecule ismore difficult to self-organize into ST ofa high orderowing to the p resence of a large variety of competing three-membered nodes.The formation of ST fractals is favored at low surface cove rage and is sensitive to tem pe ratu re.Furtherm ore,to testw he ther the assembly pa thw ay and outcome could be controlled bymolecular design,we guided the self-assembly process form ing ST fractal into the otherwise disfavored self-assembled structures using templates different from the assemblingmolecules. The temp lates are designed to actas“catassemblers”that initiate the self-assemb ling butare excluded from the finalassembled structure.

Self-assembly;Monte carlo simulation;Fractal;Sierpińskitriangle;Catassembly

O647

rnst,K.H.Top.Curr.Chem.2006,265,209.

10.1007/128_ 036

doi:10.3866/PKU.WHXB201611252

www.whxb.pku.edu.cn

Received:September 7,2016;Revised:November25,2016;Published online:November25,2016.

*Corresponding author.Email:gaoyq@pku.edu.cn;Tel:+86-10-62752431.

Theprojectwas supported by theNationalNatural Science Foundation of China(91427304,21573006,U1430237,21233002,21125311)and National Key Basic Research Program of China(973)(2012CB917304).

国家自然科学基金(91427304,21573006,U1430237,21233002,21125311)和国家重点基础研究发展规划项目(973)(2012CB917304)资助©Editorialofficeof Acta Physico-Chim ica Sinica

doi:10.3866/PKU.WHXB201612081

www.whxb.pku.edu.cn