X射线荧光光谱分析中谱线重叠校正系数的测量

葛颖新, 张环月, 唐 侠

(1. 沈阳产品质量监督检验院, 沈阳 110022; 2. 大连理工大学 材料科学与工程学院, 大连 116023; 3. 沈阳黎明发动机公司技术中心, 沈阳 110043)

X射线荧光光谱分析中谱线重叠校正系数的测量

葛颖新1, 张环月2, 唐 侠3

(1. 沈阳产品质量监督检验院, 沈阳 110022; 2. 大连理工大学 材料科学与工程学院, 大连 116023; 3. 沈阳黎明发动机公司技术中心, 沈阳 110043)

应用整套标准样品法和基本参数(FP)法计算谱线重叠校正系数(K)效果较好。应用整套标准样品法需选用与被测样品具有相同基体和近似组成的标准样品;由于共存组分的谱线重叠的干扰常导致校正曲线产生较大的负截距,需通过多次迭代计算消除截距而使曲线通过原点,因为只有这样得到的K和M才是真值。实践中常有一些例子不能用整套标准样品法计算K值,例如钢中测定低含量铬时受到钒的重叠干扰问题。在此实例中除了钒对铬的谱线重叠干扰之外,还有仪器通道材料的干扰,此时,必须先用瑞利散射校正法消除此干扰后,选用铁基的标准样品,用FP法计算K值,可消除钒对铬的谱线重叠干扰。

X射线荧光光谱法; 谱线重叠校正系数; 基本参数法

X射线荧光光谱分析中谱线重叠现象普遍存在,文献[1-3]中给出了一些元素间存在的谱线重叠干扰。由于重叠校正系数与所用设备的几何条件,准直器、晶体、脉冲高度分析器,探测器能量分辨率有关,所以重叠校正系数只能在所用仪器上由试验算得,不能直接引用文献数值[1],因此准确测得重叠校正系数是每一位X射线荧光光谱分析者首要解决的问题。测量重叠校正系数一般有两种方法。一是应用仪器自带软件计算法。仪器自带软件计算法应用较多,目前商品X射线荧光光谱仪都有此类软件。以标准样品绘制校准曲线,采用经验系数法、理论影响系数法(理论α系数法)等在校正基体效应的同时计算得到重叠校正系数。使用该方法时因标准样品数量及分析元素含量范围有限,软件计算出的重叠校正系数的准确性有限,这些基体效应校正软件多用于定性和半定量分析[4],由软件计算得到的重叠校正系数甚至会出现负值[5-7],得到错误结果,或出现不该有的元素间重叠[8]。原因很可能是软件不能将基体效应中增强效应所致的增强与谱线重叠时产生的增强区分开来。二是直接测量法。文献[9]中介绍的直接测量方法有两种:① 纯物质测量法,选择干扰元素的纯物质为标准样品,分别测量干扰元素在分析元素分析线位置和干扰元素参照线位置的强度,重叠校正系数等于前者强度除以后者。纯物质测量法简单、快速,但有时难以获得纯物质。② 整套标准样品法(即多次迭代的校正曲线法),选择同时含有分析元素和干扰元素的整套标准样品,绘制校准曲线,根据计算公式线性回归计算出重叠校正系数。

本工作中给出了利用基本参数(FP)法灵敏度工作曲线来测量重叠校正系数的方法,为试验中快速、准确测得重叠校正系数提供了新的途径。

1 试验部分

1．1 仪器

岛津XRF-1800型顺序式X射线荧光光谱仪(4 kW铑靶,FP工作软件)。

1．2 仪器工作条件

管电流80 mA,管电压40 kV,面罩10 mm,测量时间为10 s,均使用标准狭缝,闪烁计数器。

1．3 试验方法

样品用粒度为0.14 mm(120号)的砂纸在金相磨光机上磨平、吹干;分析硅元素时应使用铝砂纸,分析铝元素时应使用碳化硅砂纸,以去除磨料的影响。分析磷元素时不用乙醇棉擦拭表面。

在仪器工作条件下,利用纯物质进行测定,以待测成分的质量分数为横坐标,对应的荧光强度为纵坐标绘制校正曲线。或利用整套标准样品进行测定,以理论荧光强度为横坐标、对应的荧光强度为纵坐标绘制FP曲线,采用荧光强度扣除法来测得重叠校正系数。

2 结果与讨论

2．1 纯物质测量法测量重叠校正系数

用纯物质测定元素间的重叠校正系数是文献[9]推荐的方法之一。试验选用纯钛样品来测量钛Kβ对钒Kα的重叠校正系数。元素间重叠干扰的典型示意图见图1。

图1 谱线重叠示意图Fig. 1 Schematic of overlap of spectral lines

由图1可得公式(1):

式中:IQ1为在Q1处测得分析元素的总强度;I1为在Q1处测得的分析元素的净强度;I1′为干扰线P3在Q1处贡献的净强度;B1为待测元素在Q1处的背景强度。

重叠校正系数(K)见公式(2):

式中:I2为干扰元素在Q2处测得的净强度,Q2处的2θ角是干扰元素的参照线的角度。

分析样品是纯钛,不含钒元素,TiKβ线在Q1处,即钒的Kα峰位处测量到的强度就是I1′。与图1不同的是,TiKβ峰在VKα峰位的右侧,故它的背景测量位置放在左侧(2θ为75.5°)。为精确测量,采用不同的电流来测定,其他测量条件见1.2节。结果见表1。

平均重叠校正系数为0.026 8。在计数探测器的线性工作区,荧光强度应与电流大小成正比,该闪烁计数器的给定线性工作上限是300 kcps,但从表1可知:当电流从30 mA增至90 mA时,强度由62.801 kcps增至187.707 kcps,K有增大的趋势,表明因计数管死时间造成的非线性已显现出来。

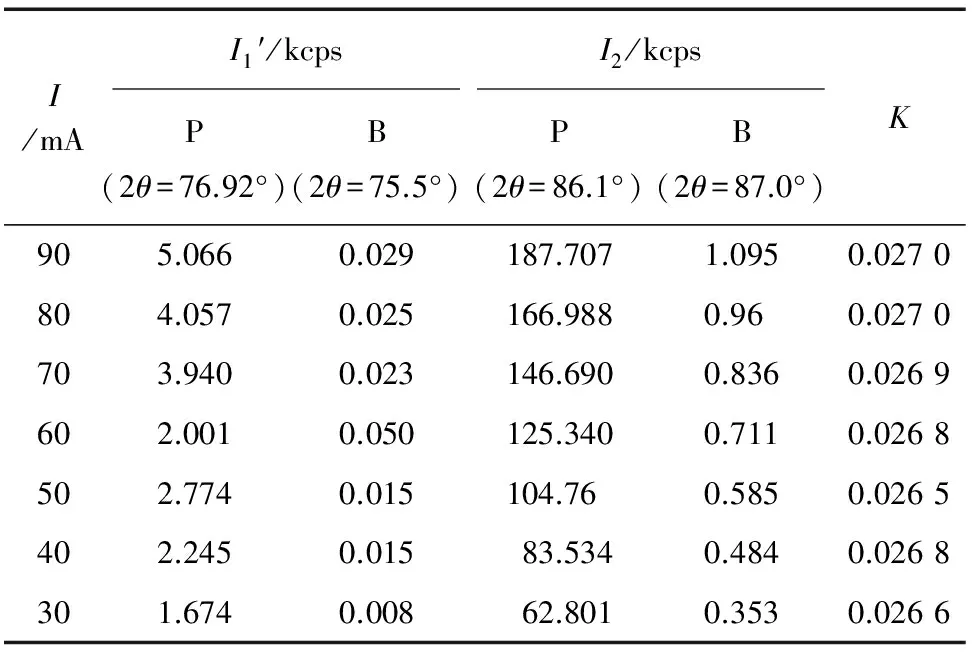
表1 用纯钛样品测得的TiKβ对VKα线重叠校正系数Tab. 1 K of TiKβ to VKα with pure titanium sample

2．2 整套标准样品法测量重叠校正系数

将公式(1),(2)联立可得公式(3):

式(4)中:C为标准样品中所含元素的质量分数;M为在所用测量条件下的灵敏度。由公式(3),(4)得公式(5):

公式(5)中有两个未知量K和M,在金属和氧化物中都可用公式(5)来计算K,理论上只需两个标准样品就可以解此二元一次方程而计算得K,较多的标准样品能测得更准确的K。在金属样品中,选择同时含有分析元素和干扰元素的整套标准样品,绘制校准曲线,该曲线斜率的倒数就是元素的M[1-2],但只有截距过原点时的K和M值才是真值,要经过多次试验,通过迭代计算得到。

试验选用我国某所研制Ti6Al4V整套标准样品和英国某公司的BST-13和BST-23标准样品,其成分列在表2中,来测量钛合金中钛Kβ对钒Kα的重叠校正系数,结果见表2。

表2 用整套标准样品测得的钛合金中TiKβ线对VKα线的重叠校正系数Tab. 2 K of TiKβ to VKα with a set of standard samples of titanium alloys

采用与表1中相同的测量条件,其中电流选用80 mA,对样品登记强度,得到图2的校正曲线,有较大的负截距,此负截距就是钛对钒的重叠干扰造成的。利用与铬的FP曲线(图5)同一界面上数据栏内的钒元素的净强度,即(IQ1-B1);再利用图2中曲线的斜率(b)为0.392 4计算出M(1/b)值,该值为2.548 kcps·%-1;记录下同一个样品在参照线TiKα位置处测得的强度I2,从而计算K的各项数据见表2,其平均值为0.025 2。将此值代入测量程序,再次登记强度,得到图3。图3中的负截距仍存在,但数值小了。图3中的b=0.401 8,M(1/b)=2.489。再进行第2轮迭代,计算ΔK的各项数据见表2,ΔK平均值为0.002 5。此时K为0.027 7(K1+ΔK)。用新K值再次登记强度,得到图4,图4中校正曲线经过原点,得到K值是钛合金中钛Kβ对钒Kα的重叠校正系数。

2．3 FP法测量重叠校正系数

在铁基合金中不能用整套标准样品法来测量VKβ对CrKα的重叠校正系数,因为铬在铁基中受到基体铁的增强,在校正曲线上低含量的点比高含量的点有较大的M值,故校正曲线本身就有较大的负截距,此外在钢铁中也很难找到高钒低铬的牌号,更不会有整套标准样品存在。类似情况可采用FP法来测量。要测量合金钢中VKβ对CrKα的重叠校正系数,首先要校正通道材料对铬造成的重叠干扰。

图2 未校正重叠的钒的校正曲线Fig. 2 Calibration curve of V before correction of overlap

图3 钒第1轮校正后曲线Fig. 3 Calibration curve of V after correction with the first iterative calculation

图4 钒第2轮校正后曲线Fig. 4 Calibration curve of V after correction with the second iterative calculation

1) FP法校正通道材料造成的重叠干扰

选用英国MBH低碳钢整套标准样品(5个样品,不含钒元素,其中铬的质量分数为0.062%～0.21%),与GSBA6800-89 1Cr18Ni9Ti含高铬的不锈钢整套标准样品(7个样品,不含钒元素),建立FP曲线,见图5。

图5中近原点处的小方格内包含了铬元素5个低含量的成分点,图6为放大图。可看出这5个点都在直线的上方,5个点的正偏差分别是0.200,0.194,0.201,0.213,0.137 kcps,高出的强度是通道材料影响造成的;在每一样品中测得铑的瑞利散射线强度分别是27.7,27.8,27.82,28.04,27.92 kcps,K等于偏差值除以瑞利散射线强度,经计算K的平均值为0.006 9,将K值加入,再次登记荧光强度,得到图7,可以看出通道材料影响得到了有效的消除。

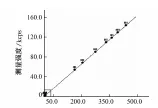
图5 铬的FP 曲线Fig. 5 FP curve of Cr

图6 低含量铬区域放大图Fig. 6 Enlarged curve of Cr with low contents

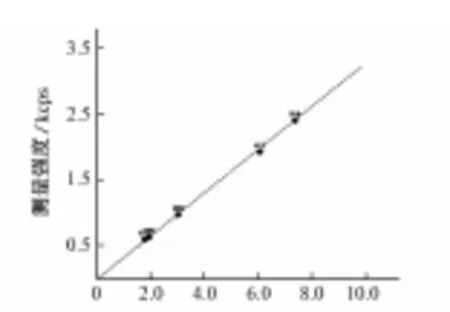
图7 校正后低含量铬FP曲线Fig. 7 FP curve of Cr with low contents after correction

2) FP法测量铁基中钒对铬的重叠校正系数

选用40088-1996高速工具钢中钒的质量分数为1.23%～3.56%,铬的质量分数为3.54%～4.59%的5个样品,和本节1)中用的不锈钢整套标准样品,在通道重叠校正系数加入后,将上述两套标准样品中铬的荧光强度登记在同一个FP曲线上,将对应高含量钒的低含量铬(质量分数为3.54%～4.59%)的5个工作点区域放大后,得到图8,这几个点都在曲线的上方,这是VKβ重叠干扰所致。通过图8同一界面的数据栏内给出的这5个点的正偏差,记录下同一个样品在参照线VKα位置处测得的强度I2,采用本节1)中相同方法计算出K的平均值为0.016,将K值计入测量程序再次登记荧光强度,得到FP曲线见图9,消除了VKβ的重叠干扰,将两套不同标准样品中较低含量和高含量的铬拟合在一条直线上。

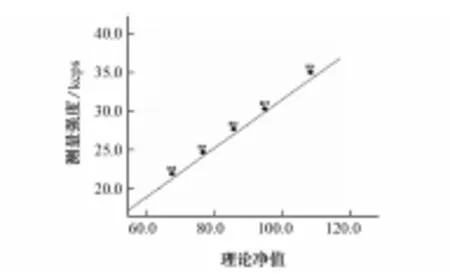
图8 低含量铬工作点区域放大图Fig. 8 Enlarged curve of Cr with low contents

图9 扣除了重叠干扰后的铬的FP曲线Fig. 9 FP curve of Cr after correction for overlap

2．4 测量重叠校正系数的影响因素

2．4．1 背景位置

测量基体元素对相邻元素重叠校正系数时,背景位置不同会对重叠校正系数影响很大。钴的2θ为52.72°,当背景(B)的2θ为53.50°时,不锈钢中铁对钴的重叠校正系数为0.019 8;测量条件相同,背景的2θ改为54.50°时,K为0.026 5。因此,测量K和应用K要用相同的背景2θ。

2．4．2 参照线

正确选择参照线是测量重叠校正系数的重要条件。参照线大多选择干扰元素的分析线,也可以选择其他线系,甚至可以选择干扰线本身。总之要使分析线和参照线之间的强度比不应受其元素的干扰而变化。

合金中MoL系Lι线(λ=0.615 0 nm)对PKα线(λ=0.615 5 nm)重叠干扰,应选MoLα线作为参照线。若选择MoKα线(λ=0.071 0 nm)作为参照线,则在参照线λ=0.071 0 nm和分析线λ=0.615 5 nm之间存在着合金系统中大部分元素的吸收线,不同元素对参照线质量吸收系数不同,造成分析线和参照线之间强度比(即K系数)不再是常数,而是随合金成分变化。文献[10]中选择MoLα线(应用了替代元素来测量该线的强度)作为参照线分析磷时获得非常好的效果。

同样,在测定铁镍基合金中钨对磷和硅的重叠干扰系数时,应选取WMα作为参照线,此时也要用替代元素来测量Mα的强度。

2．4．3 面罩大小、电流和电压的变化

以镍基合金中钛对钒重叠校正系数测量为例,选用GH4037整套标准样品中样品4(钛的质量分数为1.80%～2.73%,钒的质量分数为0.11%～0.63%),其他测量条件不变,分别改变面罩大小、电流、电压来考察这些因素对重叠校正系数的影响,结果见表3。

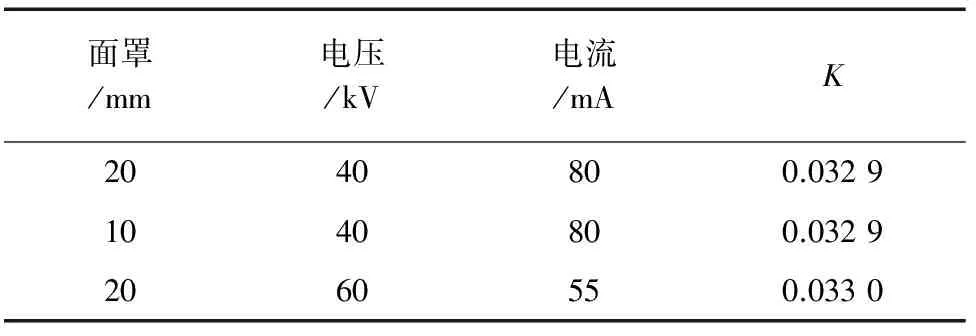
表3 不同面罩、电流、电压下测得的镍基合金中TiKβ对VKα线的重叠校正系数Tab. 3 K of TiKβ to VKα with Ni-base alloy under different apertures, currents and voltages

由表3可知:在满足谱线充分激发的条件下,K与实际分析中所采用的电压、电流和面罩大小无关。

2．4．4 狭缝的影响

以铁基合金中CrKβ对MnKα重叠校正系数测量为例,说明狭缝大小变化对重叠校正系数的影响。选用GSBA6800-89 1Cr18Ni9Ti的7个不锈钢样品(锰的质量分数为0.356%～1.983%,铬的质量分数为7.40%～20.75%)。用整套标准样品法测量K(除狭缝外,其他测量条件不变),结果见表4。较细的狭缝会改善谱线重叠程度,同时也改变了分析线和参照线的荧光强度,K与狭缝大小有关。

表4 参照线与分析线用了不同的狭缝测得的重叠校正系数Tab. 4 Values of K measured at different slit width for analytic line and reference line

2．4．5 不同基体对谱线重叠的影响

选用不同标准样品用相同的测量条件分别测量了纯钛、钛基、镍基、铁基中TiKβ对VKα的重叠校正系数,依次为0.026 8,0.027 7,0.032 9,0.027 3。说明谱线的K与基体相关。基体不同,相关元素受基体的吸收或增强不同,从而K不同。

2．5 特殊情况下重叠校正系数的测量

2．5．1 用替代元素处理基体元素对相应元素的重叠干扰

基体元素对相邻元素重叠干扰出现在钛到锌等过渡元素,有钛合金中的钛对钒,铁基合金中的铁对钴,钴基合金中的钴对镍,镍基合金中的镍对铜,铜合金中的铜对锌等。此类重叠校正系数的测量选用整套标准样品法和FP法均可,在选用参照线时要特别注意:若用干扰元素的Kα作为参照线,除钛合金中的钛对钒外,其余4个合金系统在分析线与参照线之间都横亘着原子序数比基体元素低一个元素的吸收限波长。如铁基合金中的铁对钴的重叠干扰:铁的λKα为0.193 7 nm,铁的λKβ为0.175 7 nm,钴的λKα为0.179 1 nm,而锰的吸收限波长为0.189 6 nm,位于铁的Kα和钴的Kα之间,此时会因锰含量的变化而影响重叠系数,应选用铁的Kβ作为参照线,即干扰线本身作为参照线。基体元素一般作为余量,因此要找一个分析系统中不存在的元素来替代基体元素,替代元素所用的2θ仍是基体元素Kβ线的2θ。

铁基合金中铁对钴的重叠,校正前后的校正曲线见图10和图11,图11中11号点的质量分数为0.005%,用整套标准样品法和FP法都可以有效得出,用后者还可消除基体效应。

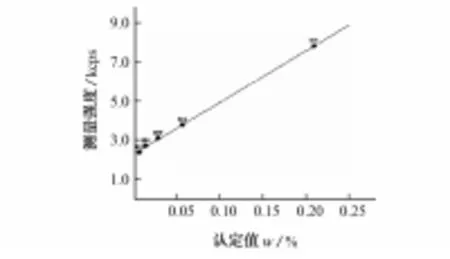
图10 未校正重叠前的钴校正曲线Fig. 10 Calibration curve of Co without correction of overlap

图11 重叠校正后的钴校正曲线Fig. 11 Calibration curve of Co after correction of overlap

2．5．2 连环重叠干扰

连环重叠干扰是指基体中A元素受到B元素重叠干扰,同时B元素又受到C元素的重叠干扰。如钒、铬共存的钛合金中,TiKβ对VKα重叠,VKβ又对CrKα重叠。在这类连环重叠干扰情况下,在测量顺序上是先测TiKβ对VKα的重叠,再测量VKβ对CrKα的重叠。强度测量顺序是钛、钒、铬,这与常规顺序相反。测出这两个重叠校正系数解决了钒铬共存钛合金荧光光谱分析中的难题[11]。美国标准[12]在Ti6Al4V钛合金的荧光分析中用Kβ作为钒的分析线,以避免基体钛对它的重叠干扰,再用假定的方式确定CrKα线对VKβ的重叠校正系数,而Kα线对Kβ线的重叠校正系数较大,低微含量铬的存在影响不大,在钒、铬共存钛合金中是不可行的。

用BST-13、BST-14、BST-15、BST-22、BST-23、BST-24和BST-5A等7个样品,采用与表2中相同的测量条件和方法,测得的VKβ对CrKα重叠校正系数为0.024。用FP法在高速工具钢上测得的VKβ对铬的重叠校正系数为0.016。再次表明在不同基体中重叠校正系数不同。在钛合金中,铬受到基体钛的强烈吸收,钒既不受到增强也不受到吸收;在铁基合金中,铬受到基体铁的增强要比钒受到的增强要大,这从铬、钒两元素对FeKα线的质量吸收系数不同中可看出。

2．5．3 一个元素同时受两个或两个以上元素干扰

选择适当标准样品,分别测出每对元素间的重叠系数,再联合使用。如钨和钼对磷的重叠干扰,可先在含高钨而不含钼的高速工具钢整套标准样品中测量出钨对磷的K值,再用含高钼的整套标准样品,含钨或不含钨都可以。若含钨,可在登记磷荧光强度时先将钨的K值代入,再测量出钼对磷的K值。

2．5．4 高次线重叠干扰

一般情况下,高次线形成的重叠干扰可用调整脉冲分布(PHD)来消除[1],但当干扰线很强时则无效,此时若分析线的PHD过窄,分析线的灵敏度会很小而不利于分析。在铜合金或铜含量高的其他合金(如蒙乃尔合金)中分析磷时就属此种情况,铜的4次线(λ为0.616 7 nm)重叠干扰磷的Kα线。可用适当标准样品测得磷的校正曲线,可能会有负截距,选用CuLα线(可找替代元素)作参照线扣除重叠干扰,会得到磷元素的过原点的校正曲线。

用纯钛测得的TiKβ对VKα的重叠校正系数是0.026 8,而用钛合金整套标准样品测得此值为0.0277,ΔK=0.000 9,此时参照线强度为151.3 kcps,要扣除的强度误差为ΔI=151.3×0.000 9=0.136 2 (kcps),在此测量条件下的钒的灵敏度为2.489 kcps·%-1,造成的成分误差ΔC=ΔI/M=0.136 2/2.489=0.055(%)。在低含量时,如此大的误差不允许,在试验中能测量出的钒元素的最低质量分数为0.013%。

整套标准样品法和FP法测量重叠校正系数快速、准确、适用性广。重叠校正系数与测量条件及基体相关,因此其测量条件和使用条件应相同。实践中应尽可能地选用合金,而不是用纯元素来测量元素间的重叠校正系数。

感谢权义宽教授级高级工程师的帮助和指导！

[1] 梁钰.X射线荧光光谱法分析基础[M].北京:科学出版社, 2007．

[2] 吉昂,陶光仪,卓尚军,等.X射线荧光光谱法[M].北京:科学出版社, 2003．

[3] 卓尚军,陶光仪,韩小元,等.X射线荧光光谱法的基本参数法[M].上海:上海科学技术出版社, 2010．

[4] 应晓浒,林振兴.X射线荧光光谱无标样分析软件在金属材料分析中的应用[J].冶金分析, 2001,21(6):41-43．

[5] 陈安源,李辉,马洪波,等.X射线荧光光谱测定不锈钢中17种元素的研究[J].冶金分析, 2012,32(2):22-27．

[6] 吕平平,安身平.X-射线荧光光谱法测定不锈钢中元素含量[J].核动力工程, 2012,35(6):167-169．

[7] 芦飞.X射线荧光光谱法测定不锈钢中多种元素[J].冶金分析, 2014,34(7):69-73．

[8] 陆晓明,金德龙,胡莹.X射线荧光光谱法测定镍铬合金中15种元素[J].冶金分析, 2013,33(10):49-55．

[9] ASTM E 1622-1994 Standard practice for correction of spectral line overlap in wavelength dispersive X-ray spectrometry[S]．

[10] 牛昌安,张鹏,腾志强,等.X射线荧光光谱法测定合金中的磷[J].理化检验-化学分册, 2015,51(2):235-238．

[11] 张环月,季守华,李春艳.X射线荧光光谱法测定铬、钒、钛共存的钛合金中12种元素[J].冶金分析, 2014,34(5):30-34．

[12] ASTM E 539-96 Standard test method for X-ray emission spectrometric analysis of 6Al-4V titanium alloy[S]．

Determination of Correction Coefficients of Spectral Overlap in XRFS

GE Ying-xin1, ZHANG Huan-yue2, TANG Xia3

(1.ShenyangProductsQualitySupervisionandInspectionInstitute,Shenyang110022,China;2.MaterialsScienceandEngineeringInstitute,DalianUniversityofTechnology,Dalian116023,China;3.TechnicalCenterofShenyangLimingAero-EngineCorporation,Shenyang110043,China)

It was shown that for determination of correction coefficients of spectral overlap (K), the method using sets of standard samples(Ⅰ) and the method of fundamental parameters (FP, Ⅱ) were suitable to be used. In applying method Ⅰ, standard samples with same matrix and similar components of testing samples should be chosen, and spectral overlap often led to negative intercept in the calibration curve. To obtain true values ofKandM, several times of iterative calculations were applied to eliminate the intercept and to make the calibration curve passing through the origin. Instances were encountered where method Ⅰ was not applicable. For examples, determination of values ofKfor elimination the interference of spectral overlap of Cr by V in determination of low contents of chromium in steels. In this case, besides the interference of overlap by V, interference due to the pathway material of the instrument was happened, and it was necessary to eliminate it first, and the correction by applying Rayleigh scattering was performed. Then the value ofKwas measured and calculated by the FP method using steel standard samples. The interference of spectral overlap of Cr by V was eliminated.

XRFS; Correction coefficients of spectral overlap; Method of fundamental parameters

10.11973/lhjy-hx201702013

2016-02-18

葛颖新(1980-),女,辽宁沈阳人,工程师,硕士,研 究方向为荧光光谱分析。E-mail:gf0624@sina.com

O657.34

A

1001-4020(2017)02-0183-07