需求随机情况下供应商的最优退货策略

邵 艳

(天津大学 理学院， 天津 300350)



需求随机情况下供应商的最优退货策略

邵 艳

(天津大学 理学院， 天津 300350)

研究了库存系统中分别存在单个零售商和两个竞争零售商的随机需求环境下各个决策变量最优解求解问题。对于未售出的产品，供货商可选择完全接收退货或不接收退货两种情况。通过比较两种情况下供货商获得的最大利润，得出最优退货策略。结果表明，供应商是否采取接收退货主要依赖于市场的需求，两个零售商的竞争对供应商退货策略没有影响。由此可以帮助供应商制定最优的退货策略，其有实际指导意义。

随机需求；退货策略；零售商竞争；利润函数

随着经济的发展和科技的进步,企业之间的竞争越来越激烈,对于具有较长的生产周期和需求不确定的产品,各企业为了争夺市场份额,供应商通常提供回购策略,允许零售商退货从而增加订货量。回购策略是供应链上游成员接受下游成员未售出产品的一种契约,这种策略在现实生活中普遍存在。PASTERNACK[1]首先研究了市场需求随机下的退货策略,说明退货策略对供应链的影响,但仅考虑了单个零售商的情况。PADMANABHAN等[2]从微观角度对退货策略进行了说明,在确定性需求下退货策略可加剧零售商的竞争,在需求随机情况下,需求较高时不接收退货,需求低时采用全部退货。MARVEL等[3]采用建模的方法得出供应商接收退货与否的关键在于顾客需求的不确定性。PADMANABHAN等[4]讨论了制造商是采用全部退货还是不退货策略取决于市场需求,给出供应商的退货策略对零售商竞争和自身利润的影响。EMMONS等[5]引入了部分未售出产品以全价退货以及以回收价格退货,得出供应商提供适当的退货价可有效提高其期望利润，不足之处在于研究中假设顾客需求随机变量服从均匀分布。DING等[6]研究由一个零售商和多个供货商组成的装配系统的退货策略。周依[7]考虑顾客退货和决策者具有风险规避态度对供应链绩效的影响。徐洪超等[8]分析了由单个按订单生产企业和众多消费者构成的系统中最优退货策略问题，得到了企业的最优退款数额和最优模块化设计水平。MANTRALA等[9]在固定批发价时，从零售商的角度研究需求函数和退货策略对最优订货量的影响。退货策略对于电子商务的发展也有着重大的影响，丁莉[10]研究了B2C电子商务中退货策略对顾客购买行为和企业利润的影响，未考虑成本和产品残值，仅考虑退货价格的影响。杜洁等[11]通过退货策略的慷慨程度和价格两个因素对需求量的影响构造了需求函数，目标是寻求最优价格和订货量以最大化需求，不足之处是认为需求量只受产品价格和供应商退货策略的影响。随后肖秀[12]继续以B2C电子商务在线零售商的退货策略为研究内容，考虑退货时间限制情况下以零售商利润最大化为目标的在线零售商最优退货模型，但没有考虑产品价值随时间的贬值问题。

笔者在前人研究的基础上，研究需求不确定情况下供应商采用退货策略的条件以及供应商的最大利润。对需求不确定且存在两个竞争零售商的库存模型给予了详细的分析，结论和单个零售商情况类似，供应商是否采取接收退货主要依赖于市场的需求，并得到两个零售商的竞争对供应商退货策略没有影响。通过比较接收退货和完全不接收退货两种情况下供应商的最大利润，从而决定供应商是否采取接收退货策略。

1 单个零售商情况

零售商的需求依赖于两个因素，该产品最初需求以及与零售价格敏感的部分，用p表示零售价格，则产品的需求可表示为：

(1)

式中:αθ>0为产品的初始需求，且需求是随机的，分为高低两种状态(θ=l或θ=h)，对应的概率分别为λ和1-λ；β>0为需求受价格影响的因子。供应商作为Stackelberg决策领导者，零售商作为Stackelberg决策跟随者，供应商和零售商拥有完全相同的市场信息，并且都是风险中性的。假设供应商产品生产费用为常数c，零售商的单位进货价格为ω。

(1)对于供应商不接收退货的情况，供应商确定进货价格ω，零售商确定产品定价与订货数量，把该问题看成两个阶段的决策过程，采用逆序递推方法依次求解多个决策变量。

当顾客需求较低时，零售商选择最优价格使得自身收益最大，收益函数为(αl-βpl)pl，则得出产品的最优定价为：

(2)

当顾客需求较高时，零售商根据需求量等于订货量进行定价，即s=αh-βph。从而得出最优定价为：

(3)

(4)

在第一阶段，供应商的利润函数为(ω-c)s，将式(4)代入利润函数后，对ω求一阶导并令导数值为零，可得供应商的最优产品定价，从而得出供应商最大利润。

(2)对于供应商接收退货的情况，当顾客需求较低时，产品的销售量等于需求量，则产品定价要使得利润(pl-ω)dl最大，对pl求导并令导数值为零得到产品最优定价为：

(5)

当顾客需求较高时，选择合适的产品定价使得期望利润最大，期望利润函数为λ(pl-ω)dl+(1-λ)(ph-ω)dh。对ph求导并令导数值为零，可得到需求较高时零售商的最优产品定价为:

(6)

表1 单个零售商模型的最优解情况

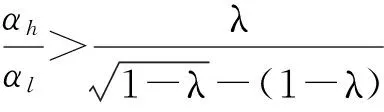
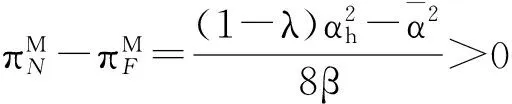
2 两个竞争的零售商情况

供应链库存系统中存在两个竞争的零售商，顾客需求不确定，同样分为高低两种状态(θ=l或θ=h)，对应的概率分别为λ和1-λ，其他参数条件和原来库存系统相同。零售商1和零售商2的需求函数分别可表示为：

(7)

(8)

其中，β>0,γ>0代表需求受价格影响的因子，满足β>γ。

(1)对于供应商不接收退货的情况，当顾客需求较低时，产品的销售量等于需求量，两个零售商(i=1,2)选择最优价格使得各自收益最大，收益函数分别为Ril=dipil=(αl-βpil+γpil)pil，令其满足一阶导数条件，可得到产品的最优定价为：

(9)

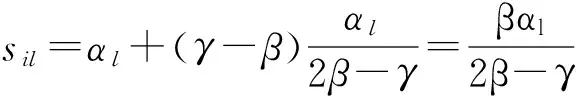
(10)

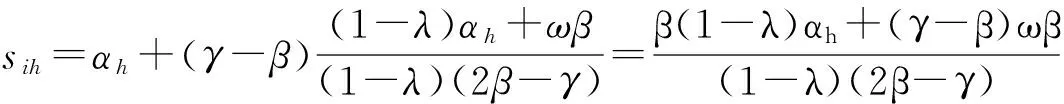
(2)对于供应商接收退货的情况，当顾客需求较低时，产品的销售量等于需求量，则产品定价使得利润(pil-ω)dil最大，关于pil求导并令其导数为零，则可得到产品的最优定价为：

(11)

当顾客需求较高时，选择合适的产品定价使得期望利润最大，期望利润函数为λ(pil-ω)dil+(1-λ)(pih-ω)dih，关于pih求导并令其导数为零，则可得到需求较高时零售商的最优产品定价为：

(12)

表2 两个竞争零售商需求不确定模型的最优解情况

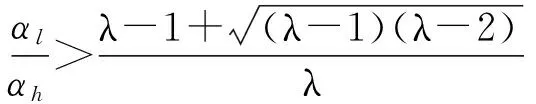
定理3 在需求不确定的双寡头竞争的市场环境下，ωF>ωN，sNl>sFl，sFh>sNh，pFl>pNl，pNh>pFh。

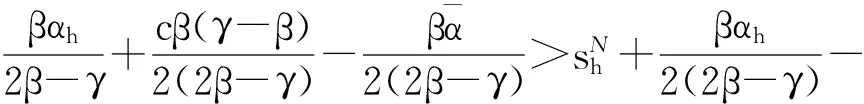
3 结论

笔者研究了需求随机情况下,单个零售商的模型以及存在竞争的两个零售商模型，目标是使得供应商期望利润最大，从而得到零售商决策变量和供应商各个决策变量的最优解。对于未售出的产品，供货商可选择接收退货或不接收退货两种情况。结果表明当供应商边际生产成本极低或为零时，在需求满足一定的条件下采取接收退货，即供应商是否采取接收退货主要依赖于市场的需求，两个零售商的竞争对供应商退货策略没有影响。研究结果对供应链管理有重要的指导意义。

[1]PASTERNACKBA.Optimalpricingandreturnpoliciesforperishablecommodities[J].MarketingScience, 1985,27(1):131-132.

[2]PADMANABHANV，PNGIPL.Returnspolices:makemoneybymakinggood[J].SloanManagementReview, 1995，37(1):65-72.

[3]MARVELHP,PECKJ.Demanduncertaintyandreturnspolicies[J].InternationalEconomicReview,1995,35(35):691-714.

[4]PADMANABHANV,PNGIPL.Manufacturer’sreturnspoliciesandretailcompetition[J].MarketingScience, 1997,16(1):81-94.

[5]EMMONSH,GILBERTSM.Theroleofreturnspoliciesinpricingandinventorydecisionsforcataloguegoods[J].ManagementSciences, 1998,44(2):276-283.

[6]DINGD,CHENJ.Supplychaincoordinationwithcontractsgamebetweencomplementarysuppliers[J].InternationalJournalofInformationTechnologyandDecisionMaking, 2007，6(1):163-175.

[7] 周依.顾客退货下考虑风险规避的供应链协调研究[D].长沙：中南大学，2012.

[8] 徐洪超，汝宜红，王英奎.按订单生产企业的最优退货策略研究[J].物流技术，2010(7)：52-54.

[9]MANTRALAMK,RARNANK.Demanduncertaintyandsupplier’sreturnspolicyforamulti-storestyle-goodretailer[J].EuropeanJournalofOperationalResearch, 1999,115(2):270-280.

[10] 丁莉.B2C电子商务退货策略[J].物流科技，2005，28(12):81-83.

[11] 杜洁，郭宸.电子商务退货策略优化研究[J].物流工程与管理，2010，32(6):116-117.

[12] 肖秀.考虑退货时间限制的在线零售商退货策略研究[D].杭州：杭州电子科技大学,2014.

SHAO Yan:Postgraduate; School of Science, Tianjin University, Tianjin 300350, China.

Supplier’s Optimal Returns Policies under Stochastic Demand

SHAOYan

The paper analyzed the optimal solutions of decision variation in the inventory system consisting of a single retailer or two competing retailers under stochastic demand. For unsold products, the supplier can choose the two cases of to fully receive the return or not receive the return.. The optimal return policy can be obtained by comparing manufacturer profit in two cases. It turned out that whether the supplier would provide return policy depended on the status of customer demand or not, and retailers' competition did not influence the supplier's return policies. The conclusions can help the supplier make optimal return policies and have practical significance.

stochastic demand; returns policy; competing retailers; profit function

2095-3852(2017)02-0232-04

A

2016-10-23.

邵艳(1990-)，女，河南商丘人，天津大学理学院硕士研究生，主要研究方向为供应链与库存管理、决策分析.

O0211.9;F724.6

10.3963/j.issn.2095-3852.2017.02.023