高速公路养护工程的“三一”目标集成管理模型

蔡文涛，刘星星，杨 青

(1.武汉理工大学 管理学院，湖北 武汉 430070；2.天津高速公路集团有限公司，天津 300384)



高速公路养护工程的“三一”目标集成管理模型

蔡文涛1,2，刘星星1，杨 青1

(1.武汉理工大学 管理学院，湖北 武汉 430070；2.天津高速公路集团有限公司，天津 300384)

高速公路的生命周期依赖于高速公路的养护工作，而高速公路的养护绩效与国家社会经济运行通畅息息相关。高速公路养护是一项复杂工作，涉及到质量、进度、成本、安全、环保、健康、风险管理等多个方面的均衡与协调，目标集成要求多目标之间可以实现主次转换、动态优化、多样操作等，通过构建三个主目标和一个附目标的“三一”目标结构理论模型，运用遗传进化算法实现高速公路养护决策的动态求解，从而为高速公路养护工作的科学决策提供依据。

高速公路养护；多目标优化；“三一”结构；遗传算法；集成管理

高速公路养护是延续高速公路生命周期的必要手段，是尽可能发挥高速公路功能的最重要保障，目前高速公路养护主要是针对病害采取补救性修复的养护方式，但往往涉及到通行、经费以及时间等多重矛盾。高速公路养护基本要求包括道路系统的可靠度与安全性，同时又能满足行驶舒适度要求。

高速公路建设是世界经济运行的重要推动力，各国都已建立了路面管理系统，包括系统建设、养护规划、成本优化等功能，为达到养护多目标均衡和优化的要求，采用了GA(genetic algorithm)[1]、SD(system dynamic)[2]、CO(constrained optimization)[3]、PERT(program/project evaluation and review technique)[4]、WBS(work breakdown structure)[5]等多种优化方法。高速公路养护的目标体系较为复杂，存在基本目标同一性和具体操作差异性的特点，KE等[6]建立了工期、成本、质量均衡优化的3种模型以满足不同决策者的管理目标。董小林等[7]运用多木桶模型阐释工程管理6个目标的动态关系。陈丽兰[8]构建了工程项目5要素协同度模型。工程中各目标之间存在非线性关系，也存在规律性关联，如工程项目的工期和质量存在近似成二次曲线的关系[9-10]。

在路面使用性能评价与预测方面，采用的评价指标一般有单项指标和综合指标两类，评价指标主要有美国AASHTO(American association of state highway and transportation officials)的路面服务性能指数PSI、加拿大的舒适性指数RCI、日本的养护管理指数MCI以及中国的路面综合评价指标PQI与行驶质量指数RQI等。预测模型有经验模型、力学预测模型、概率模型、关系模型、灰色系统预测法、马氏距离法、人工神经网络法等。中国的路面管理研究始于20世纪80年代，主要是通过引进国外技术，如英国的CHART (computerised highway assessment rating and treatment)、芬兰的FPMS(Finland pavement management system)和世界银行的HDM-III(highway development and management-III)，并在此基础上加以分析改进，目前我国已形成一套中国路面管理系统CPMS(China pavement management system)[11]。

随着图像技术、互联网、云计算技术及物联网技术的拓展与应用，路面管理系统的应用性得到进一步提升，而对于系统管理的复杂性，路段的力学性能、养护规划和路网结构等问题依然受到资源条件的限制，诸多目标难以协调。质量、工期、成本是工程建设最为主要的控制目标，安全、环保、风险管控等是工程建设的重要目标，各目标之间难以协调一致，尤其在外部环境变动的情况下，工程管控则更为困难。笔者在多目标集成管理的基础上，设计高速公路养护“三一”目标控制体系，并运用动态多目标优化算法求解，以实现目标转换的有效对接。

1 高速公路养护多目标优化问题

1.1 高速公路养护概念

高速公路养护的常规目标是路面使用性能最大化与养护资金最小化，两者都是工期、质量与成本等具体目标的合成。路面管理系统的基本目标是在保证一定道路服务水平的基础上，尽可能地延长公路的生命周期。高速公路的养护不仅涉及到交通问题，更关系到人财安全、物流通畅及物资调配等社会经济问题。

1.2 高速公路养护技术指标

路面养护需求分析包含路面检测和方案设计两个主要步骤。当前，路面检测技术在不断更新，为养护工作带来了巨大的便利，而养护的核心技术指标则基本未变。在进行路面养护需求分析时，每条公路的情况都不尽相同，需要对道路进行考察分析，包括道路的里程、路面类型、车道数等技术指标，以及道路的通车时间和交通量等运营指标，同时路段在路网中的重要程度、社会影响和经济影响等也需要考虑。

根据高速公路路面的《高速公路养护质量检评方法》、《公路技术状况评定标准》、《公路沥青路面养护技术规范》等相关规范和标准的规定，一般需要检测的路面基础数据包括：国际平整度指数(IRI)、路面破损率(DR)、路面弯沉(l)和路面横向力系数(SFC)。在路面检测现状数据的基础上，对路网中各线路各路段分别计算道路质量指数(RQI)、路面状况指数(PCI)、抗滑性能指数(SRI)和路面结构强度指数(PSSI)，然后综合计算路面行驶质量指数(PQI)，PQI是对道路的养护需求及路网运行总体状况的基本评价。

2 高速公路养护工程“三一”目标模型

2.1 高速公路养护工程的“三一”目标结构

高速公路养护工程目标基本上蕴含了质量(quality)、成本(cost)、工期(time)、健康(health)、安全(safety)、环保(environment)6个目标的信息，QCT(quality、cost、time)是常规且最为主要的基本目标，HSE(health、safety、environment)是根据实际情况具有不同重要性的目标[12]。

由于高速公路养护工程具有复杂性、动态性、开放性、非线性的特点，而工程管理要求系统性、协同性、创造性，因此有必要建立高速公路养护工程多目标集成管理模型。可根据综合集成评价函数和各主成分(转换为三个主目标和一个附目标)的得分排名进行高速公路养护工程目标结构塑造。针对动态目标，探求目标之间的层次、显隐、强弱关系。将主成分设为基本维度，剩余目标合成附维度，共同合成一个目标锥体。多目标四维集成图如图1所示。

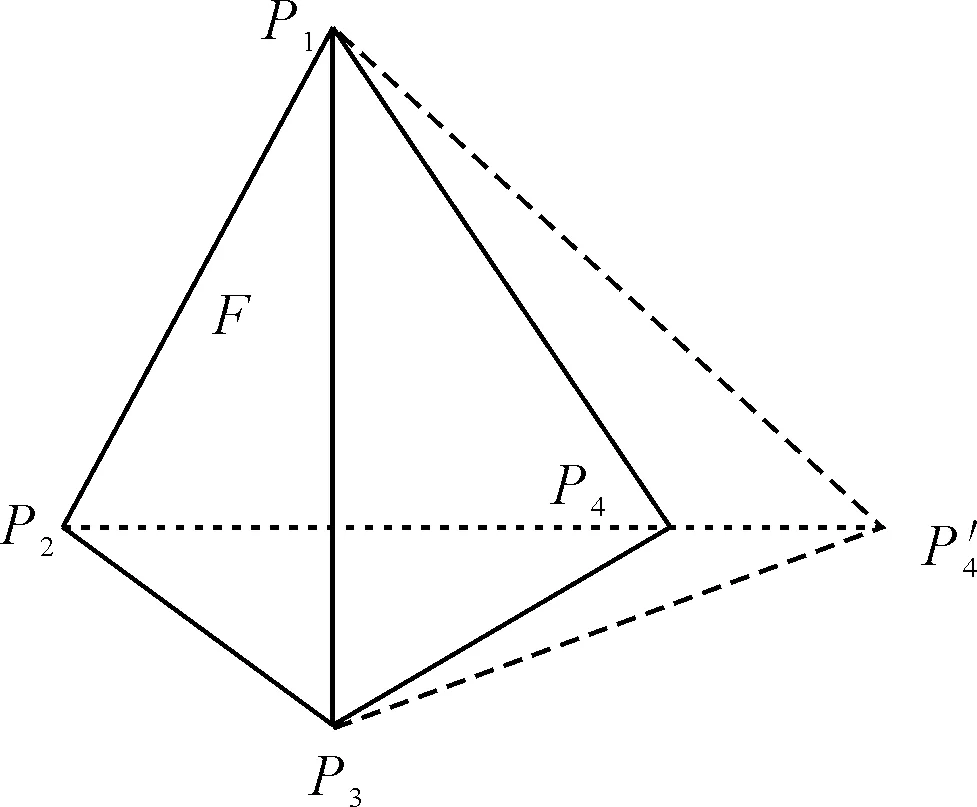
图1 多目标四维集成图

2.2 高速公路养护工程的“三一”目标集成管理

(1)高速公路养护工程目标集成。笔者所构建的“三一”目标集成体系中，仅将QCT之间的关联关系以函数的形式量化，HSE与QCT的关联关系主要通过参数设定来约束。将目标锁定为4项主要目标后，经过组合，可以得到如表1所示的4种基本组合。

表1 高速公路养护工程“三一”多目标基本组合

在实际工程项目中，难以达到项目工期最短、成本最低和质量最高的理想目标。建立3者之间的关系模型并充分考虑附目标，尽可能达到多方相对满意的解，或部分目标满意，其他目标可容忍的解。根据文献[13]～文献[15]，建立QCT目标优化模型：

(1)

(2)

maxQ=f(IRI,DR,SRI,SFC,lR,l0)

(3)

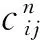
在满足QCT目标体系的同时，同时需考虑HSE问题，但作为次要问题，在工程建设中按技术标准实施，不改变QCT目标“体积”。最小安全距离 MSDE可作为道路的安全性指标[16]。环境污染费用成本计算是全寿命路面养护决策中最为棘手的问题之一，目前国内外研究尚无成熟理论和计算方法。可将由于交通延误和施工建设产生的环境污染，以排放量大小的形式进行考虑。笔者选取安全距离(S)和碳排放量(E)作为HSE的核心指标：

(4)

式中：VL为前车车速；D为车头时距；VF为后车车速；PRT为车辆安全时距；f为路面摩擦力系数；g为道路纵坡；Gk为第k种气体的排放量；Фk为第k种气体的排放转化因子。

HSE=wS·S+wE·E

(5)

其中高速公路大中修工程QCT多目标体系是最为常见的，也是最为关键的目标体系，Q-C、C-T、Q-T都存在若干双目标关联关系，在求解QCT多目标问题时，必须考虑3者之间的关联约束。

一般情况下，工序的直接成本会随着工序时间的缩短而增加，并呈现出边际递增的趋势，即工期压缩越多，直接成本增长得越快，如人员增加、材料增多、设备增设等。工序的间接成本会随着工序的持续工作时间的缩短而减少，如现场管理费、设备租赁费等。

一个工程的整体质量水平是由各工序的质量水平集成而得，高速公路养护工程的各工序都有详细的养护标准和工艺，按照技术要求完成养护工程，则工程的整体质量是可以得到保障的，而出现的纰漏则主要依靠风险管控和工程检验技术来弥补。通常情况下，高速公路养护工程建设采用标准招投标工作，投资规模往往经过严格的预算，而最佳养护对策则要求以养护投资规模为约束，实现效益最大和路面养护质量最佳。

(2)高速公路大中修工程多目标集成处理。对约束条件的处理通常有两种方法：约束偏离值方法和约束偏离度方法[17]。约束偏离值方法是将约束偏离值加到每个个体的目标函数上，或将约束偏离值作为一维目标函数值。

(6)

式中：C(x)为个体x的约束偏离值；cj(x)为第j个约束偏离值；wj表示第j个约束函数的加权值，通常wj=1/q；gj(x)≤0(j=1,2，…,q)；hj(x)=0。

由于用来操作染色体的遗传算子常常产生不可行后代，如离散分布、约束范围等。GEN等[18]提出了适应性罚函数来处理不可行个体。在当前种群p(t)中给定一个个体x，其适应性罚函数为：

(7)

其中，bi(x)为第i个目标函数的值。对于约束的设计，一般可采用引入罚函数的方法，将约束条件转化为罚函数，然后将罚函数与适应度函数进行整合，使不满足约束条件的个体适应度函数值小于满足约束条件的个体适应度函数值，最后通过遗传算法中的优胜劣汰实现对不满足约束条件个体的剔除。

(8)

式中：λ为目标权重；p取值为2。

3 实例应用

笔者从质量、工期和成本3个维度考量高速公路养护决策，根据技术指标与预算，形成“工期-成本-质量”(T-C-Q)目标函数组。

(9)

式中：工期单位为百天；成本单位为亿元；质量单位为效用。ev-MOGA[19-20]算法中θ是一类混合型多属性参数，其中设t为θ1；c为θ2；IRI为θ3；DR为θ4；SRI为θ5；SFC为θ6；lR为θ7。由于高速公路养护方案具有一套完整的技术参考标准，且实施严格的招投标管理，故参数θ3～θ6均在高速公路养护标准的误差范围内微调，主要的变动因子在于成本c与工期t。

笔者选取天津某高速公路养护工程的实况作为案例，由于养护项目(尤其是大中修工程项目)多采取外包形式，养护的技术工艺与项目规划均采用格式化管理，故不考虑具体的技术操作，所探讨的问题主要围绕工程中灵活变动的因素所产生的T-C-Q绩效，例如工期安排中的调度问题。养护工程中工期变动模式如图2所示。

图2 工期灵活变动模式

假设工序A、B、C分别在ti、tj、tk开工，工期分别为Ti、Tj、Tk，但均存在变动空间。为测试笔者所研究的方法，选取其中1 000 m高速作为测算对象。假定整个项目日平均间接成本为1 000 元/天。根据预算和网络计划图，最大工期为210天，最小工期为156天，最大成本和最小成本分别为2 100.55万元和1 803.79万元。各工序的最差质量均设为0.80～0.90。

笔者运用ev-MOGA算法进行测算，参数设置情况：搜索空间为三维空间，交叉概率为0.10～0.25，变异规模为20，变异概率为0.10，每一周期保留的Pareto集合数为100，迭代次数为100。经过模拟，得到Pareto前沿面、Pareto集合及最优解。通过Matlab运行，得到在第38周期工期、成本、质量的单目标最优解分别为1.002 35、0.000 062 527 7、-11.726，其中质量是由max转换为min，因此最优解为11.726，单目标最优解满足Pareto条件，但不能确定多目标最优解。该案例选用单目标最优解作为最优理想点，通过标准欧式距离测算，选择距离最短的作为全局多目标最优解。模拟结果如图3～图6所示，分别表示养护工程中工期、成本、质量以及三者Pareto解的演化过程。

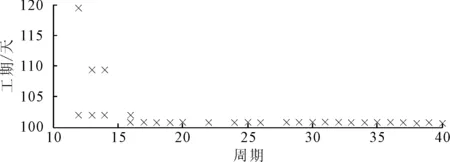
图3 工期演化

图4 成本演化

图5 质量演化

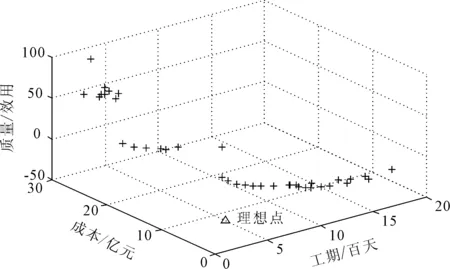
图6 高速公路养护Pareto解与理想点

通过设置理想点，计算距离得到高速公路养护的工期、成本、质量多目标最优值为(11.764 1，1.509 92，-11.518 2)，通过与理想点对比发现，工期压缩并不能达到多目标最优的情况，而成本压缩也存在诸多不现实的情况，但在工期按期完成且成本可控的情况下，工程建设的总体水平能维持在一个较高水平。通过高速公路养护“三一”目标结构的构建，运用ev-MOGA算法求解，通过寻优区间设置优化搜索范围，故在高速公路养护多目标决策时能应对突发的情况，如天气、交通等因素，所得到的测算结果更真切有效。

4 结论

面向复杂的高速公路养护工作，多目标优化模型能综合考虑多个目标，将工程多个目标函数的效用最大化处理。从工期、成本、质量3个主维度考虑高速公路养护工程绩效，并集成安全、健康、环保，实现多目标的转化。笔者在“三一”多目标结构的基础上，动态求解各类高速公路养护多目标决策模型，求解效率高并且能更为合理地处理变化因素。模型所需参数设置较多，但由于具有进化机制，计算结果对参数输入的敏感性降低，经过仿真运算可求得一系列收敛性和多样性俱佳的Pareto最优解，为高速公路养护工作计划决策提供了参考依据，对其他领域类似的模糊多目标优化问题也具有一定的参考价值。

[1] FWA T F, TAN C Y, CHAN W T. Road-maintenance planning using genetic algorithms. II: analysis[J]. Journal of Transportation Engineering, 2014,120(5):710-722.

[2] FALLAH-FINI S, RAHMANDAD H, TRIANTIS K, et al. Optimizing highway maintenance operations: dynamic considerations[J]. System Dynamics Review, 2010,26(3):216-238.

[3] ZIARATI K, AKBARI R, ZEIGHAMI V. On the performance of bee algorithms for resource-constrained project scheduling problem[J]. Applied Soft Computing, 2011,11(4):3720-3733.

[4] AZARON A, TAVAKKOLI-MOGHADDAM R. Multi-objective time-cost trade-off in dynamic PERT networks using an interactive approach[J]. European Journal of Operational Research, 2007,180(3):1186-1200.

[5] KUMBHARE A G, SIMMHAN Y, FRINCU M, et al. Reactive resource provisioning heuristics for dynamic dataflows on cloud infrastructure[J]. IEEE Transactions on Cloud Computing, 2015,3(2):105-118.

[6] KE H, MA W, CHEN X. Modeling stochastic project time-cost trade-offs with time-dependent activity durations[J]. Applied Mathematics & Computation, 2012,218(18):9462-9469.

[7] 董小林,陈美玲,宋赪,等.基于多木桶模型的工程管理目标体系构建及应用[J].建筑经济,2015,36(9):56-60.

[8] 陈丽兰.基于协同学的工程项目五要素集成管理模型研究[J].工程管理学报,2016,30(6):101-105.

[9] BABU A J G, SURESH N. Project management with time, cost and quality considerations[J]. European Journal of Operational Research, 1996,88(2):320-327.

[10] SALMASNIA A, MOKHTARI H, ABADI I N K. A robust scheduling of projects with time, cost and quality considerations[J]. The International Journal of Advanced Manufacturing Technology, 2012,60(5):631-642.

[11] 徐旭,刘巍,殷晓.基于系统可靠度的道路养护优化方法[J].中外公路,2015,35(2):307-311.

[12] 王华,孙宏福.基于Petri网的工程项目多目标协同优化研究[J].工程管理学报,2015,29(1):134-138.

[13] 伊长生,高建炳.基于模糊规划的工程项目工期-成本-质量均衡优化研究[J].工程管理学报,2015,29(1):129-133.

[14] 高贺,柴士超.基于模糊数学理论的工程成本-工期研究[J].武汉理工大学学报(信息与管理工程版),2015，37(6):786-789.

[15] 颜丽敏,李千登,王云龙.基于WBS-RBS与RS方法的油气管道穿越工程风险评价研究[J].安全与环境工程,2016,23(3):135-139.

[16] MASOUD N, ZARRILLO M L, GARTNER N H. Traffic flow with increasing density assuming a simple safe stopping distance formula[J]. International Journal of Forecasting, 2013,29(1):122-130.

[17] 尚荣华,焦李成,胡朝旭,等.修正免疫克隆约束多目标优化算法[J].软件学报,2012,23(7):1773-1786.

[18] GEN M, CHENG R, OREN S S. Network design techniques using adapted genetic algorithms[J]. Advances in Engineering Software, 2001,32(9):731-744.

[19] HERRERO J M, BLASCO X, MARTINEZ M, et al. Non-linear robust identification of a greenhouse model using multi-objective evolutionary algorithms[J]. Biosystems Engineering, 2007,98(3):335-346.

[20] LAUMANNS M, THIELE L, DEB K, et al. Combining convergence and diversity in evolutionary multi-objective optimization[J]. Evolutionary Computation, 2002,10(3):263-282.

CAI Wentao:Doctorial Candidate; School of Management, WUT, Wuhan 430070, China.

Integrated Management Model of ‘Three-One’ Target Structure for Expressway Maintenance Project

CAIWentao,LIUXingxing,YANGQing

The life cycle of expressway depends on the maintenance, whose performance is closely related to the smooth running of national economy. The maintenance of expressway is a complex work, which involves the balance and coordination of quality, schedule, cost, safety, environmental protection, health, risk management and so on. Goal integration can achieve hierarchical conversion in multiple objectives, dynamic optimization and diversity control. This paper constructs three main objectives with a secondary objective called as 'three-one' target structure. Then it utilizes genetic evolutionary algorithm to achieve dynamic solution of expressway maintenance decision-making,therefore, this work can enhance the scientific decision-making of various highway maintenance projects.

expressway maintenance； multi-objective optimization； ‘three-one’ structure；genetic algorithm； integrated management

2095-3852(2017)02-0191-06

A

2016-11-26.

蔡文涛(1974-)，男，天津人，武汉理工大学管理学院博士研究生，主要研究方向为工程管理.

国家自然科学基金项目(71603197);国家社会科学基金项目(16ZDA45);中央高校基本科研业务费专项资金项目(173203002).

U416.2；C934

10.3963/j.issn.2095-3852.2017.02.015