基于条件Shannon熵和VPRS的网络攻击策略评价方法

程 瑞，雷 璟，程 静

(中国电子科技集团公司电子科学研究院，北京 100041)



基于条件Shannon熵和VPRS的网络攻击策略评价方法

程 瑞，雷 璟，程 静

(中国电子科技集团公司电子科学研究院，北京 100041)

在回顾现有网络攻击评价技术的基础上，指出了现有方法不能完全由数据驱动和不能实现有效攻击规则在线提取的不足。由此，提出了一种基于条件Shannon熵和变精度粗糙集理论(VPRS)的网络攻击策略有效性评价方法，该方法完全由数据驱动。同时，综合运用遗传算法和VPRS理论对有效攻击规则进行智能提取。并通过实例说明了该方法的有效性。此技术能够为我国网络空间安全评价及攻击策略智能调用提供技术支撑，保障我国网络空间安全。

条件熵;变精度粗糙集;网络攻击；智能调用；数据挖掘

随着信息化水平的不断提高，网络安全的重要性日益凸显。赛博空间安全研究具有十分重要的战略意义，已经引起了国内多位研究者的关注[1-3]。形式多样的网络攻击事件带给人们的不仅是沉重的教训，更多的是启示和指导。如何从已经发生的攻击事件所组成的经验知识库中进行有效的数据挖掘和分析，从攻防两个维度对不同攻击策略的攻击效果进行评价，并从中提取出针对特定目标的高效攻击策略是一项具有较大社会和科研价值的研究。

已有研究者在网络攻击效果评价方面做了相关工作:许多研究者使用层次分析法建立了网络安全评价分析方法[4-8]，如文献[4]提出了一种基于灰色层次分析法的网络攻击危害性评估指标量化方法，但是其判断矩阵的获得是通过专家打分获得的，其结果很大程度上依赖于专家个人的主观判断；SWILER等[9]提出了基于图的网络脆弱性评估方法，以及最小攻击代价分析方法和最短路径分析方法；ZAKERI等[10]提出使用描述逻辑进行脆弱性分析，但其所提出的评价方法均仅适合于单一的、逻辑关系清晰的攻击策略研究，并不合适处理大量攻击数据及组合攻击策略的效果评估。现有的网络攻击效果评价研究多注重攻击效果评价，缺少智能攻击规则的提取[11-14]。如文献[11]提出了一种基于模糊综合评价的IMS网络攻击后果评估方法，通过实例验证了评价方法的有效性，但该方法的输出结果仅包括不同攻击策略的整体效果评价，无法实现满足要求的攻击策略的快速在线提取。文献[12]运用网络分析法(analytic network process, ANP)构建评估的网络结构模型，从而对攻击效果进行量化的评估，但其研究也仅有评价，缺乏有效规则的提取能力。

粗糙集理论作为一种处理不确定、不完备信息的有效方法，其数据分析过程完全由数据驱动，将其与其他智能算法结合可以同时实现方案评价与规则提取，进而有效克服上述研究中的不足。为此，笔者开展以下研究工作：①提出了一种基于条件Shannon熵和VPRS的网络攻击策略评价与智能调用方法。同时，创新性地将网络攻击的手段和效果指标放入一个评价体系中，并考虑各级指标之间的勾稽关系，提高了评价结果的客观性；②为了弥补现有方法无法兼顾“评价”与“规则在线提取”的短板，融合遗传算法和变精度粗糙集理论，提出了一种有效功能攻击规则的智能提取及调用算法；③笔者所提出的评价方法不依赖于先前的经验知识，完全由数据驱动，通过计算得到每个网络攻击方案的攻击效果的客观评价。该方法为网络智能攻击策略的效果评价与在线智能调用提供了一种新的思路，对于提高特定目标的网络空间安全具有较高的应用价值。

1 基于条件Shannon熵和VPRS的多因素网络攻击策略效果评价

1.1 粗糙集理论

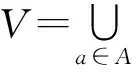
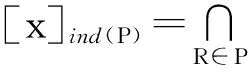
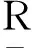
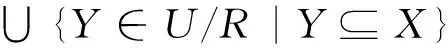
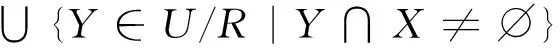
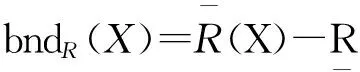
1.2Shannon熵

SHANNON把信息熵定义为离散随机事件的出现概率，其定义式如式(1)所示。信息熵可以理解为某种特定信息的出现概率。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，其信息熵就越高。信息熵表明了信源整体的统计特征，是总体的平均不确定性的量度。对于某一特定的信息源，其信息熵是唯一的。

(1)

设U为对象集合，条件属性集C和决策属性集D为U上的等价关系子集。C和D的等价类在U中的分布情况X、Y分别为：X=(X1,X2,…,Xm)和Y=(Y1,Y2,…,Ym)，则条件信息熵H(D|C)为在获知C的条件下D的不确定程度，其计算公式为：

(2)

式中：P(Xi)为Xi(i=1,2,…,m)的概率；P(Yj|Xi)为在已知Xi的情况下Yj(j=1,2,…,n)的条件概率。当对数取为2时，H(D|C)的单位为bit。

1.3 基于Shannon熵和VPRS的网络智能攻击策略评价及优化方法

为解决现有网络攻击效果评价与智能决策中的问题，笔者构建了多因素网络攻击效果综合评价指标体系,并提出了一种基于Shannon熵和VPRS的网络智能攻击策略评价及优化方法，具体步骤如下：

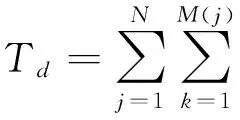
一般而言，当网络遭受攻击后，其安全性能会有所下降，各安全分指标所对应的网络熵为：

(3)

式中：V1为遭受攻击前的网络安全指标值；V2为遭受攻击后的网络安全指标值。

总的网络熵可以认为是不同网络安全评价指标网络熵的加权平均值。

(4)

综合评价模型中的条件属性包含了网络攻击的常用技术，总体可分为主动攻击和被动攻击。主动攻击包括网络阻塞、权限控制、信息伪造3个二级指标。其中，网络阻塞包括信道资源强占、网络连接强占、存储空间强占3个三级指标；权限控制包括口令攻击、脚本程序漏洞攻击、缓冲区溢出攻击3个三级指标；信息伪造包括IP地址欺骗和虚假消息类欺骗两个三级指标。被动攻击包括网络监听和信息窃取两个二级指标。 其中，网络监听包括基于软件的监听和基于硬件的监听两个三级指标；信息窃取包括网络扫描、体系结构探测和系统服务信息收集3个三级指标。具体的多因素网络智能攻击评价指标体系如图1所示。

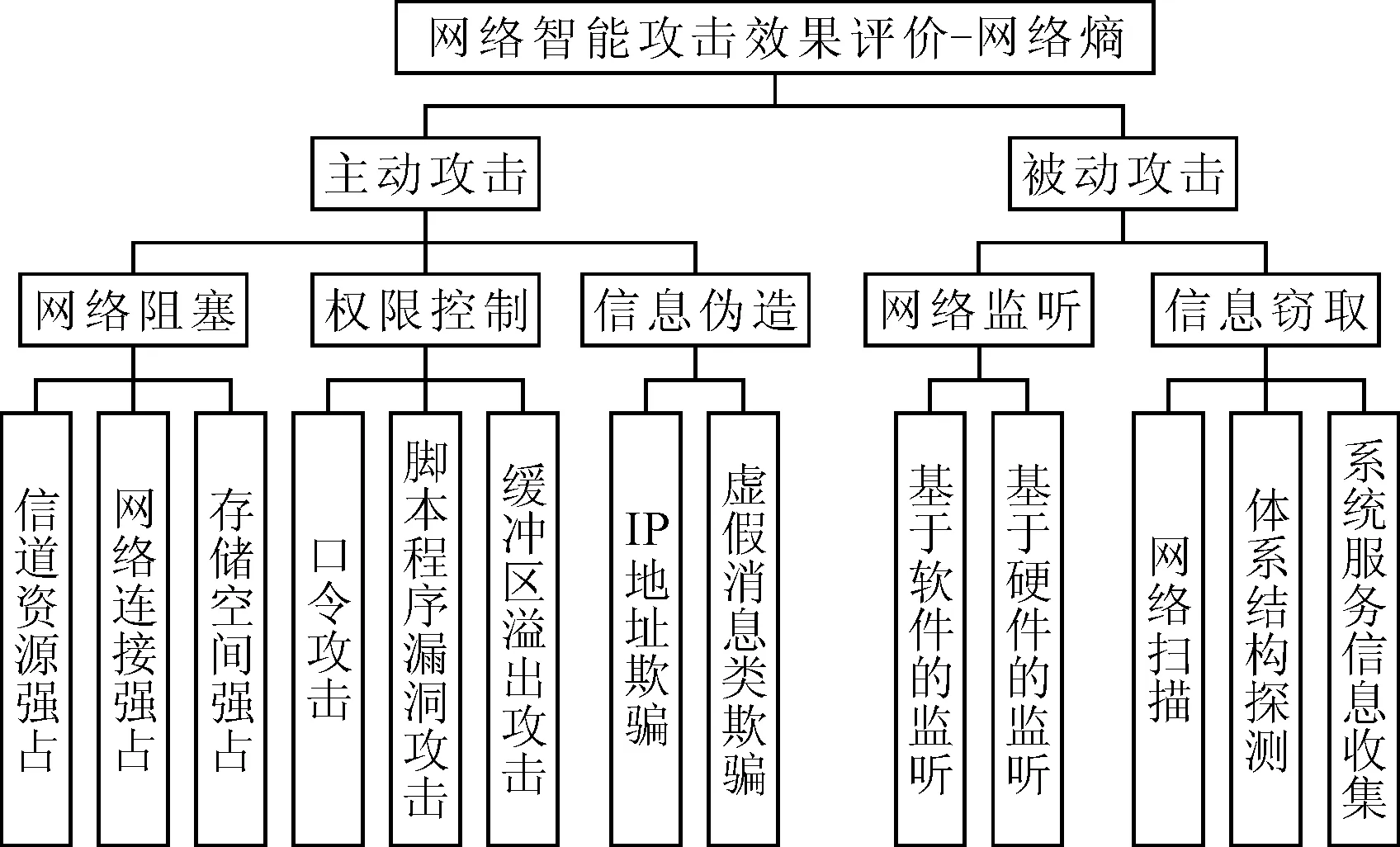
图1 基于Shannon熵和VPRS的网络攻击效果 多因素综合评价指标体系图

(2)数据离散化与预处理。为确保离散结果的客观性，笔者使用Naive Scaler 算法对原始数据表进行离散。Naive Scaler 算法不需要额外的参数，能够根据信息系统或数据库本身进行离散化处理。笔者使用波兰华沙大学与挪威科技大学联合开发的Rosetta软件自动实现Naive Scaler 算法，算法对每个属性，根据属性值由小到大的顺序对决策表中的实例进行排序，然后进行判断，对于两个相邻实例，在属性值和决策值均不同时，将两个属性值的平均值作为断点值。该算法依据具体的条件属性值和决策属性值选取断点值，忽略信息系统的不可区分关系，随着数据库本身的数据排列情况不同，得到的断点也不相同。Naive Scaler 算法选取断点的过程是起初设断点集为空集，逐步增加断点得到离散化结果。

(3)基于多级指标的网络攻击方案评价算法。设由网络攻击方案组成对象集合U，U中又包括L个对象，b=1,2,…,L，每个对象对应一个网络攻击方案；对象集合U中的网络攻击方案所使用的网络攻击方法组成条件属性集合C，C包括N个二级指标，i=1,2,…，N，每个二级指标又包括M个三级指标，j=1,2,…,M；网络攻击方案的攻击效果为决策属性D。

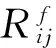
按照式(5)计算每个对象的攻击效果值TC，TC越高，说明对象Ub的攻击效果越好：

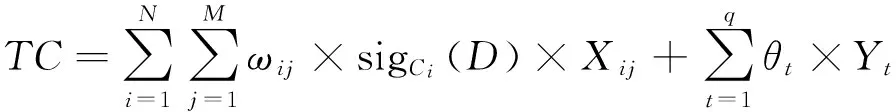
(5)

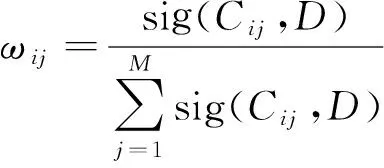
(6)

式中：Xij为对象Ub在三级指标Cij下的决策值；ωij为三级指标Cij对于决策属性D的重要性权重，ωij∈[0,1]；sigCi(D)为二级指标Ci对于决策属性D的重要性权重；Yt为对象Ub在决策属性D下的决策值；θt为决策属性D对于条件属性集合C的重要性权重；sig(Cij,D)=H(D|Li0)-H(D|Li)，表示在三级指标集合Li中去除三级指标Cij前后条件熵的变化值，其中Li为二级指标Ci对应的三级指标集合，Li0为Li中去除三级指标Cij后的三级指标集合，H(D|Li)和H(D|Li0)的计算公式为：

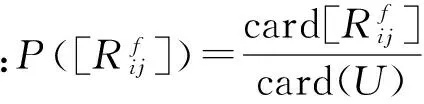
二级指标Ci对于决策属性D的重要性权重sigCi(D)，按照式(7)进行计算：

(7)

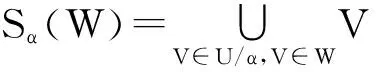
进一步地，所述决策属性D对于条件属性集合C的重要性权重θt，按照式(8)进行计算：

(8)

(4)使用变精度粗糙集(VPRS)结合遗传算法对相关规则进行挖掘并存入知识库，以实现后续对于特定目标有效攻击策略的智能调用。笔者使用具有较好全局优化能力的遗传算法对变精度粗糙集模型进行规则提取。遗传算法是一种群体性操作，这种操作以群体中所有个体为对象。主要有选择、交叉和变异3个操作算子，遗传算法的构成要素主要有：染色体编码、个体适应度评价、遗传算子(选择算子、交叉算子、变异算子)以及遗传参数设置等[16]。

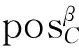
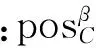
accuracy(β)=card({x∈U|f(x,d)=τ})

support(α·β)=card({x∈U|

对决策规则进行筛选的标准一般是每条决策规则的支持数(support)和覆盖度(coverage)，支持数即论域中属性值与规则匹配的对象数，对象数越多，则这条规则的强度越大；覆盖度用于估计决策规则的质量，覆盖度揭示了在满足决策规则的决策类条件下满足条件类的概率。为了提取有效的规则，必须剔除掉那些支持数和覆盖度较低的决策规则，归纳出对于决策者比较有用的决策规则。

2 算例分析

2.1 攻击方案有效性多因素评价

为了说明上述方法的有效性，笔者针对一实例进行分析。考虑如下的应用场景：为了对特定目标A进行网络攻击，攻击者使用10种不同的组合攻击策略发动了网络攻击，其中，不同组合攻击策略包含攻击手段的种类及强度均不相同，记录了被攻击目标A在受到不同攻击方案前后各项网络安全关键指标的变化情况，结合网络熵的计算公式，计算不同组合攻击策略的网络熵，作为评价指标体系中的决策属性值。10种不同的组合攻击方案及其攻击效果所构成的离散后的决策表如表1所示，应用所提出的算法进行计算分析，最终得出不同方案攻击有效性的排序，并从中进行规则挖掘，以提高后续攻击的有效性。

按照前述方法，分别计算出其他各三级指标的相对重要性权重以及各二级指标对于决策属性的重要性权重，计算结果如表2所示。

从表2可以看出，三级指标中的口令攻击在二级指标权限控制中的相对重要性为零，三级指标体系结构探测在二级指标信息窃取中的相对重要性为零，增加这两个指标对于完善针对目标的网络攻击效果并无作用，因此，可以将这两个指标从评价指标体系中剔除。

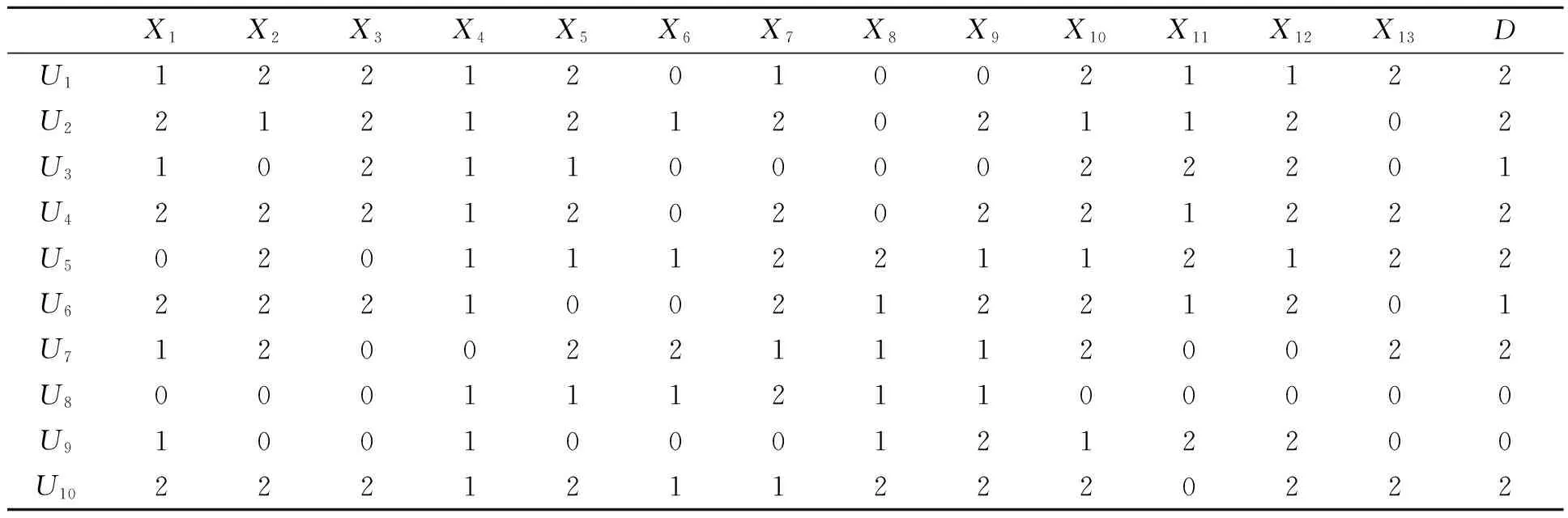
表1 攻击目标A多因素网络智能攻击策略评价决策表

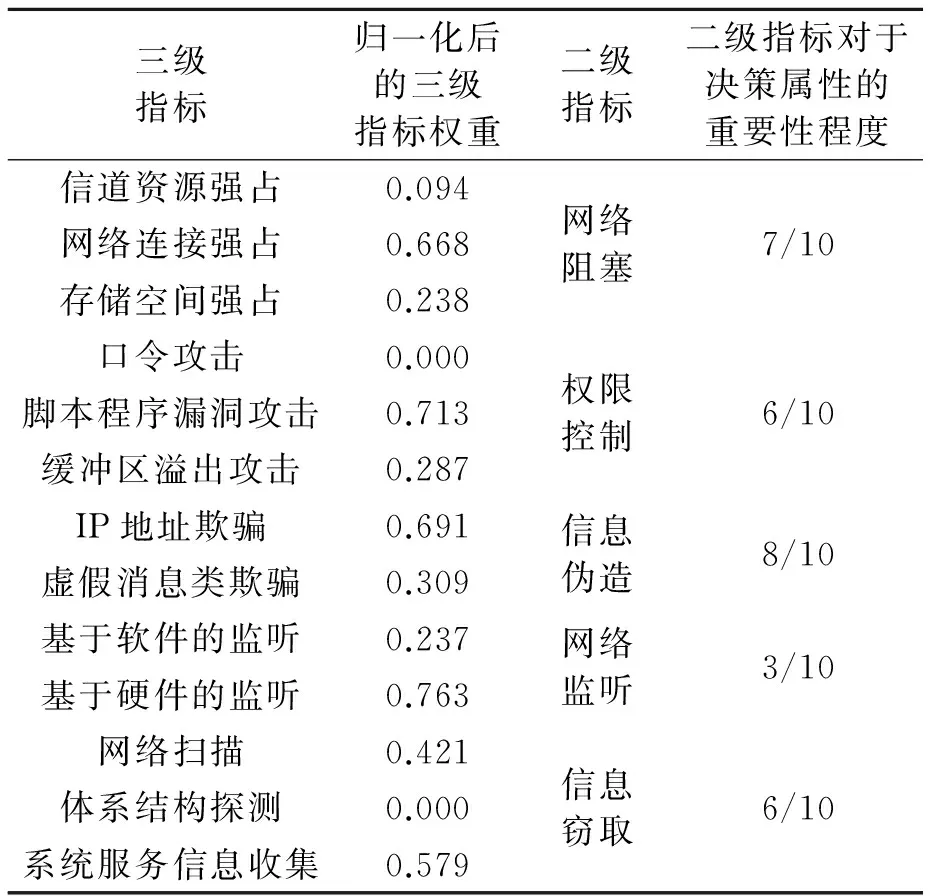
表2 基于条件Shannon熵计算得出的各级指标权重值

再按照式(5)、表1和表2，计算每个对象Ub的攻击效果值TC。按照从大到小的顺序对各个对象Ub的攻击效果值TC进行排列，结果如下：攻击方案4 (6.908 6)≻攻击方案10(6.769 8)≻攻击方案5(6.635 2)≻攻击方案7(6.224 7)≻攻击方案1(6.147 8)≻攻击方案2(5.689 5)≻攻击方案6(4.605 4)≻攻击方案3(2.789 8)≻攻击方案8(2.023 9)≻攻击方案9(1.1893)。

从综合评价结果来看，攻击方案4较为综合地运用了强烈的主动及被动组合攻击策略，因此，其对于目标的攻击效果较为显著。而攻击方案9则主要运用了被动攻击策略，因此，其攻击效果不甚明显。

2.2 有效攻击方案智能调用

综合评价的结果是为了进行有效攻击规则的智能调用，以便进行知识库的更新和有效规则挖掘。使用遗传算法对决策表进行数据挖掘和规则提取后，得出了53个属性约简和509条规则。这些规则中，有些规则具有很强的实用性和决策意义，有些规则却是偶然的。所以需要对所得出的决策规则进行提取，从而得出对于特定目标实施有效攻击的有效决策规则。在对所得出的规则进行筛选之后，得出如表3所示的具有较高代表性的决策规则。

表3 由遗传算法和VPRS提取的具有代表性的攻击规则

3 结论

笔者提出了一种基于条件Shannon熵和变精度粗糙集理论的网络攻击策略多因素评价和智能攻击策略调用方法。相较于传统方法，基于条件Shannon熵和粗糙集理论的综合评价方法完全由数据驱动，无需依赖于任何先验知识，因此所得的评价结论更加客观准确。从案例分析的结论还可得出，主动攻击、被动攻击相结合的组合攻击策略可以更为有效地对特定目标进行攻击。基于遗传算法和VPRS的智能攻击规则在线获取算法，可以自动提取满足精度要求的攻击策略，并将其存储到知识库，为后续智能攻击调用提供指导。

但是，针对笔者所提出的算法在实际攻击场景中的应用效果，尚需通过构建高仿真或真实的实验环境进行验证；同时，如何结合云计算编制相关软件及平台，保证算法的快速有效运行，实现网络攻击策略智能评价、决策与调用的一体化控制，这将是后续研究的重点工作。

[1] 吴巍.赛博空间与通信网络安全问题研究[J].中国电子科学研究院学报，2011，6(5)：473-476.

[2] 赵捷，赵宝献，王世衷.关于赛博空间与赛博空间作战问题的思考[J].中国电子科学研究院学报，2011，6(3)：235-239.

[3] 仇建伟.赛博空间作战研究[J].中国电子科学研究院学报，2011，6(3)：254-255.

[4] 王燮，刘孙俊，唐毅谦，等.一种基于灰色层次分析法的网络攻击危害性评估指标量化方法[J].成都大学学报(自然科学版)，2012，31(1)：57-60.

[5] 李雄伟，于明，杨义先，等.Fuzzy-AHP法在网络攻击效果评估中的应用[J].北京邮电大学学报，2006，29(1)：124-127.

[6] 董艳，成和平.层次分析法在合理选择网络攻击时间中的应用[J].四川师范大学学报(自然科学版)，2006，29(6)：756-758.

[7] 李雄伟，周希元，杨义先.基于层次分析法的网络攻击效果评估方法研究[J].计算机工程与应用，2005，41(24)：157-159.

[8] 刘进，王永杰，张义荣，等.层次分析法在网络攻击效果评估中的应用[J].计算机应用研究，2005，22(3)： 113-115.

[9] SWILER L P, PHILLIPS C. A graph-based system for network-vulnerability analysis [C]∥Proceedings of the 1998 Workshop on New Security Paradigms. New York: ACM, 1998:71-79.

[10] ZAKERI R, JALILI R, HAHRIARI H R, et al. Using description logics for network vulnerability analysis[C]∥Proceedings of the 5th International Conference on Networking. Mauritius: IEEE, 2006:78-83.

[11] 郭严赞，季新生，刘彩霞，等.一种基于模糊综合评价的IMS网络攻击后果评估方法[J].计算机应用研究， 2013，30(11)：3400-3403.

[12] 王艳莉，赵楠，王云峰.基于网络分析法的网络信息系统攻击效果评估研究[J].科技信息，2009(15)：452-453.

[13] 孙飞显.一种受危险理论启发的网络攻击态势评估方法[J].计算机工程与应用，2012，48(2)：8-10.

[14] 邓新颖，杨庚，姚放吾，等.基于多阶段网络攻击的网络风险评估方法研究[J].计算机工程与应用，2006，42(18)：133-135.

[15] 蒋朝哲.粗糙集理论在多属性决策中的应用研究[D].成都：西南交通大学，2006.

[16] 赵杰雪，丰洪才，杨琳.基于遗传算法的多模态视频场景分割算法[J].武汉理工大学学报(信息与管理工程版)，2015，37(6)：841-845.

CHENG Rui:Engineer; Institute of Electronic Science, China Electronics Technology Group Corporation, Beijing 100041, China.

Evaluation Method of Network Attack Strategy Based on Conditional Shannon Entropy and VPRS

CHENGRui,LEIJing,CHENGJing

Based on the literature review of existing network attack evaluation technologies, it points out that the existing methods can not be completely driven by data and can not achieve effective attack rules on-line extraction of the shortcomings. A novel network attack strategy evaluation method based on the conditional Shannon Entropy and Variable Precision Rough Set (VPRS) is put forward. This method is fully driven by input data without any priori knowledge. In addition, the effective network attack rules are derived by simultaneously using Genetic Algorithm and VPRS. A case study is presented to show the effectiveness of the proposed method. The methodology can offer a solid technological support for domestic cyberspace safety evaluation and intelligent attack rules invocation, which can guarantee the security of cyberspace in our country

conditional entropy; variable precision rough set (VPRS); network attack; intelligent invocation; data mining

2095-3852(2017)02-0162-06

A

2016-10-26.

程瑞(1987-)，男，安徽合肥人，中国电子科技集团公司电子科学研究院工程师，博士，主要研究方向为智慧城市与网络安全.

TN97;TP391

10.3963/j.issn.2095-3852.2017.02.009