无患子的压缩力学特性试验及有限元分析

2017-05-10姚立红徐道春

中国油脂 2017年4期

关键词：破壳果壳侧向

隆翔，姚立红，徐道春

(北京林业大学工学院，北京 100083)

应用技术

无患子的压缩力学特性试验及有限元分析

隆翔，姚立红，徐道春

(北京林业大学工学院，北京 100083)

为了提高无患子果壳破壳率，研究了无患子果壳破壳力学特性。首先在电子万能试验机上进行整果压缩试验，然后运用有限元法对无患子果壳的3个受力方向进行应力与应变分析。结果表明：无患子水平向、侧向、垂向的平均破壳力分别为122.08、95.13、157.24 N，弹性模量分别为49.62、40.27、50.16 MPa，平均变形率分别为13.1%、9.5%、11.4%；受力方向对破壳力、弹性模量的影响极显著；无患子果壳是各向异性的，垂向的抗压能力最强，水平向次之，侧向最小；在水平向和垂向受压时，屈服强度和变形量较大，在侧向受压时较小；有限元仿真结果与试验结果基本一致，说明所建立的仿真力学模型可以用来分析研究无患子果壳的力学特性，为无患子破壳机的设计提供了理论基础和仿真优化方法。

无患子；破壳；弹性模量；力学特性；有限元分析

无患子(Sapindusmukorossi)果实具有十分重要的开发利用价值。其果壳中含有的皂苷和苷元均具有非常强的非离子表面活性，可作为优良的纯天然洗涤剂[1-2]；在工业上，可以用来制造牙膏、洗发膏和香皂等；在医学上，可以用来止咳、化痰、退烧等[3-4]。无患子种仁可食用，含有丰富的脂肪和蛋白质，种仁含油率高达42.7%[5]，是一种新型的制取生物柴油的重要原料。无患子油品质优良，是一种良好的工业用油，可制作优质润肤剂和润滑油等[6]。

无患子成熟晾干后，首先进行脱壳处理，以便壳与仁分别加工利用。由于针对无患子的系统研究较少，大部分工业应用方面的技术是借鉴其他相似油料的应用研究。就我国目前的总体状况来看，现有的无患子脱壳设备普遍存在破壳率低、生产效率低和脱壳工艺复杂等问题[7]。因此，研制适合无患子脱壳的脱壳机就显得尤为重要。而研制适宜无患子脱壳机首先应得到无患子的破壳力学参数。

目前，在农作物的损伤规律研究方面，国内学者运用有限元法对板栗、龙眼、荔枝、澳洲坚果、冬小麦和核桃等农业物料的相关力学特性进行了大量研究[8-13]，这些研究结论表明：运用有限元法可以仿真模拟农业物料受载过程、分析农业物料的固有力学特性和损伤规律。但目前尚未见运用有限元法对无患子力学特性进行分析的研究报道。

本文选用无患子为试验材料，对其在不同的压缩方向下进行力学特性试验，得出无患子果壳分别在3个方向的破壳力、屈服强度、弹性模量和变形率。然后运用有限元法对无患子的3个受压方向进行应力及应变分析研究，获得其不同方向的破壳力学特性，并与试验结果对比分析。研究结果可为无患子脱壳机的设计提供理论基础。

1 材料与方法

1.1 试验材料

试验材料均采自福建省建宁县无患子种植示范基地，无患子果实饱满，无损伤、无虫害、外形呈球形，按照传统工艺，自然干燥，含水率为12.0%～16.0%。如图1a所示，以种脐和种脐线为参照，无患子可分为沿水平向、侧向和垂向3种受压方式；如图1b所示，无患子果实由果壳与果核两部分构成，在无患子破壳取核时，选用果壳与果核已分离的干燥无患子，破壳率较好。

a b

图1 无患子几何形状及挤压试验形式(a)和结构(b)图

试验采用深圳市瑞格尔仪器有限公司制造的电子万能试验机。试验过程中可动态显示位移变化、变形量、力、载荷速度和力-位移变化试验曲线，同时试验数据可由微机自动处理，获得弹性模量、屈服强度、最大载荷等重要力学参数。该机最大载荷10 kN，位移测量精度±0.1%，载荷精度±1.0%。电子游标卡尺：量程0～150 mm，精度0.01 mm，上海世达工具有限公司。

1.2 试验方法

试验采用刚性圆平板压缩方式，下压板设定不动，上压板以设置的下压速率5 mm/min垂直下压。无患子随机分3组，每组30个，用游标卡尺测出3组无患子的直径，并算出每组的平均值；为确保试验结果的准确性，分别以水平向、侧向、垂向受压的方式在万能试验机上做压缩试验，如图1a所示，直至果壳开裂，每组试验重复30次。测出3组无患子平均屈服强度和平均破壳力，同时统计出每次试验所得的变形量，并算出平均变形率。

采用刚性圆平板对果实加载时，根据赫兹接触理论[14]，可用下式计算果壳的弹性模量

式中:E为果壳的弹性模量，MPa；F为无患子的破壳载荷，N；μ为果壳的泊松比；D为在接触点果壳的压缩变形，mm；R为果壳的半径，mm。

1.3 仿真方法

1.3.1 建立几何模型

无患子整果由果壳和果核构成，如图1b所示。含水率为12.0%～16.0%的无患子果壳与果核均已分离；无患子破壳时主要是果壳受力，因此只需建立其果壳的三维模型，并将果壳简化为有固体属性的脆性材料。无患子试验破壳后用游标卡尺测出果壳壳厚，无患子果壳的厚度是不均匀的，呈现由顶部到底部逐渐变厚的特点，顶部壳厚为0.87～1.43mm，底部壳厚为2.51～3.47mm，取区间中间值建模。通过前期无患子几何特征测量和文献[6]可知，无患子外形近似为球形或椭球形，本文把无患子果壳简化为球形建模，直径为试验数据的平均值21.13mm，在所建模型上用细缝表达种脐部位特征，并在球模型两端放置两块平行钢板模型。

1.3.2 网格划分

用三维建模软件Solidworks建立相应的三维模型，并导入有限元仿真软件Ansysworkbench中。在分析软件中，把钢板模型设置为Solid186单元，无患子模型设置为Solid187单元，接触单元设置为CONTA174和TARGE170共同构成，接触单元是用来计算果壳模型与钢板模型之间的相互作用。大多数生物物料的泊松比在0.2～0.5以内，考虑到无患子果壳的材质与一般木材很接近，其泊松比取0.32[14]。对于含水率为12.0%～16.0%的无患子果壳，其表现为脆性材料，破裂形式为脆性破裂，因此破裂准则设置为脆性破裂破坏准则。无患子果壳的密度为0.536g/mm3，根据试验结果，无患子果壳垂向、侧向、水平向的弹性模量分别为50.16、40.27、49.62MPa。无患子果壳模型网格划分后，如图2所示。

图2 无患子果壳有限元网格划分模型

1.3.3 施加载荷

试验发现，无患子果壳水平向被压破所需的平均力为122.08N，侧向被压破所需的平均力为95.13N，垂向被压破所需的平均力为157.24N。在上端钢板模型中心施加垂直于钢板的无患子果壳平均破壳力F，下端钢板设置为固定约束，如图1a所示。

2 结果与分析

2.1 无患子压缩破壳试验

分别对3组无患子沿3种受力方向进行压缩试验。每组试验重复30次，获得的各组数据取平均值，结果见表1。

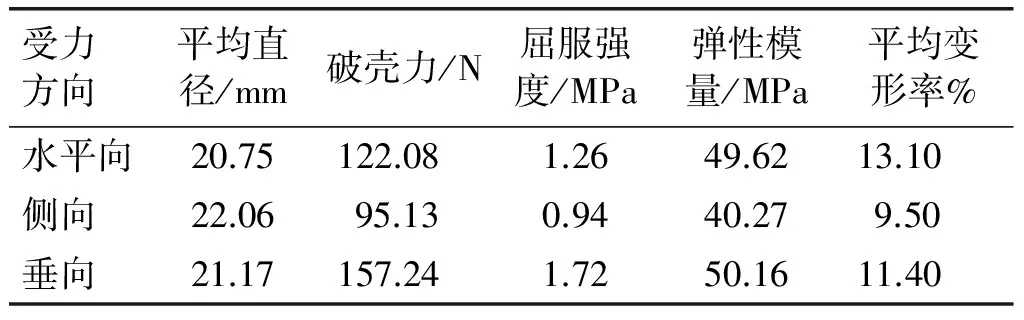
表1 不同受力方向无患子的力学特性

由表1可知，无患子果壳沿水平向、侧向、垂向受力的平均破壳力分别为122.08、95.13、157.24 N，表明垂向所需破壳力最大，因为垂向破壳时，受力点垂直于种脐部分，只有当加载力足够大，压力才能传递到果壳较脆弱部分或种脐线，才能使果壳开裂，所以所需力最大。当侧向破壳时，压力直接作用于种脐线，因此侧向受压很容易使无患子果壳破裂，所需加载力较小。无患子果壳水平向、侧向、垂向的弹性模量和屈服强度各不相同，表明果壳具有各向异性的特征，垂向时抗压能力最强，水平向次之，侧向最弱。无患子水平向破壳时平均变形率最大，侧向最小。试验中无患子垂向受压时的最大破壳力为223 N，生产中为保证果壳破裂，在设计破壳机时，施加于无患子果壳的破壳力应不小于250 N。

用Excel统计分析软件对无患子压缩试验数据进行方差分析，结果见表2。

表2 无患子压缩力学参数方差分析

由表2可知，受力方向对屈服强度、平均变形率的影响不显著，而对破壳力、弹性模量的影响极显著。

2.2 无患子力学特性的有限元分析

在压缩载荷作用下的无患子果壳的应力应变分布对无患子果壳破裂和机械脱壳的研究有着非常重要的意义。对分别沿侧向、垂向、水平向受压的无患子果壳进行有限元模拟，分别得到无患子果壳在3个方向受压的应力图、应变图和总变形图，如图3所示。

由图3可知，无患子果壳沿垂向受压时，果壳的最大应力大于水平向受压，侧向受压时最小；果壳沿水平向受压时，果壳的最大变形大于垂向受压，侧向受压时最小。无患子果壳在侧向和水平向受压时，应力应变没有一定的方向性，较大应力应变沿受力面延伸至整个果壳表面；而垂向受压时，应力应变在受力面附近比较集中，与表1对比分析可以看出，通过有限元模拟分析得出的结论和试验得出的结论一致。

将运用有限元仿真分析得到的力-位移曲线与无患子果壳压缩试验得到的力-位移曲线进行对比，如图4所示。

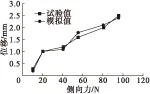
由图4可知，试验值和模拟值之间的最大、最小偏差分别是11%和3%，说明运用有限元法研究无患子果壳的破壳力学特性是可行的。原因可能是压缩试验数据的误差、果壳模型简化的几何形状与无患子果壳实际形状之间的偏差、实际受力点与数值建模受力点的误差、实际无患子果壳的材料属性参数的误差等。

3 结论

(1)通过对无患子果壳进行压缩试验，得到无患子水平向、侧向、垂向的平均破壳力分别为122.08、95.13、157.24 N；弹性模量分别为49.62、40.27、50.16 MPa；平均变形率分别为13.1%、9.5%、11.4%。

(2)试验结果表明，无患子果壳是各向异性的，当含水率在12.0%～16.0%时，垂向受压时破壳力最大，水平向受压时次之，侧向受压时最小；屈服强度和变形量沿垂向和水平向受力时较大，在侧向受力时较小；在设计无患子破壳机时，尽量使果壳沿侧向受力。

(3)运用有限元分析法模拟无患子果壳分别沿侧向、垂向和水平向受压的力-位移曲线，并与试验结果对比，得到最大偏差为11%，说明运用有限元法研究无患子果壳的破壳力学特性是可行的。

(4)试验结果显示，大部分无患子果壳受压缩载荷时，由种脐位置产生裂纹导致破壳。有限元仿真结果显示，无患子果壳沿侧向和垂向受力时，较大应力出现在种脐附近，说明所建立的仿真力学模型可以用来分析研究无患子果壳的力学特性。

[1] 姜翠翠，卢新坤，叶新福，等. 无患子的特征特性与栽培技术[J]. 东南园艺，2014(6): 118-121.

[2] 黄素梅，王敬文，杜孟浩，等. 无患子的研究现状及其开发利用[J]. 林业科技开发，2009, 23(6): 1-5.

[3] 张勤，彭求贤，蔡红兵，等. 无患子的研究进展[J]. 医药导报，2012, 31(9): 1171-1173.

[4] 邵文豪，刁松锋，董汝湘，等. 无患子种实形态及经济性状的地理变异[J]. 林业科学研究，2013(5): 603-608.

[5] 王娜，伍恒，翁震，等. 无患子种仁油特性及微波预处理提取无患子种仁油工艺研究[J]. 中国油脂，2013,38(8): 1-3.

[6] 姜翠翠，叶新福，卢新坤，等. 无患子研究进展概述[J]. 福建农业学报，2013，28(4): 405-411.

[7] 贾黎明，孙操稳. 生物柴油树种无患子研究进展[J]. 中国农业大学学报，2012，17(6): 191-196.

[8] 涂灿，杨薇，尹青剑，等. 澳洲坚果破壳工艺参数优化及压缩特性的有限元分析[J]. 农业工程学报，2015，31(16): 272-277.

[9] 张克平，黄建龙，杨敏，等. 冬小麦籽粒受挤压特性的有限元分析及试验验证[J]. 农业工程学报， 2010，26(6): 352-356.

[10] 王维，贺功民，王亚妮. 核桃的力学特性及有限元分析[J]. 中国农机化学报， 2013，34(6): 103-106.

[11] 张荣荣，李小昱，王为，等. 基于有限元方法的板栗破壳力学特性分析[J]. 农业工程学报，2008，24(9): 84-88.

[12] 陈燕，蔡伟亮，邹湘军，等. 荔枝的力学特性测试及其有限元分析[J]. 农业工程学报，2011，27(12):358-363.

[13] 卿艳梅，李长友，黄汉东，等. 龙眼力学特性的有限元分析[J]. 农业机械学报，2011，42(6): 143-147.

[14] 周祖锷. 农业物料学[M]. 北京：农业出版社, 1994: 40-50.

Compression mechanical properties test and finite element analysis ofSapindusmukorossi

LONGXiang,YAOLihong,XUDaochun

(SchoolofTechnology,BeijingForestryUniversity,Beijing100083,China)

In order to improve the breaking rate ofSapindusmukorossinutshell, the breaking mechanical properties ofSapindusmukorossinutshell was studied. The compression test of whole fruit was carried out on the electronic universal testing machine, then finite element method was applied to analyze the stress and the strain of the three forced directions of nutshell. The results showed that the average shell breaking force ofSapindusmukorossiwere 122.08, 95.13, 157.24 N, elastic modulus were 49.62, 40.27, 50.16 MPa, and average deformation rate were 13.1%, 9.5% and 11.4% respectively in the horizontal, lateral and vertical directions. The effects of forced direction on shell breaking force and elastic modulus were extremely significant, andSapindusmukorossinutshell was anisotropic, with the strongest compression capacity of vertical direction, followed by that of horizontal direction, and the minimal one of lateral direction. The yield strength and deformation amount were larger in the horizontal and vertical directions and they were smaller in the lateral direction. Simulation result of finite element analysis was basically consistent with the experimental result, and it was illustrated that the established mechanical model could be used to analyze the mechanical properties ofSapindusmukorossinutshell, providing theoretical basis and simulation optimization method for the design of shell breaking machine.

Sapindusmukorossi; shell breaking; elastic modulus; mechanical property; finite element analysis

·广告·