基于数据驱动的一类复杂系统动态特性分析

郭玲利,王目树,王 烨

(1.北京科技大学 自动化学院,北京 100083; 2.长治学院 数学系, 山西 长治 046000)

基于数据驱动的一类复杂系统动态特性分析

郭玲利1,2,王目树1,王 烨1

(1.北京科技大学 自动化学院,北京 100083; 2.长治学院 数学系, 山西 长治 046000)

针对一类复杂的无法对其机理建模的离散时间系统，根据采集的两年工艺参数数据，结合复杂工艺特点，提出了基于数据驱动的系统动态特性建模方法，构建了时间序列受控回归滑动平均(CARMA)胞映射模型;在模型结构确定的基础上，采用改进的量子行为粒子群优化(IQPSO)算法对系统参数进行辨识;算法通过设计新的粒子更新式增加了粒子的多样性，避免了算法的早熟收敛；算法通过在后期将搜索到的最优值传递给神经元作为初始权值，利用神经元增强算法的局部搜索能力，实现了算法探索与开发的平衡，达到对模型参数进行快速精确辨识的目的;在转化为状态空间模型基础上，根据胞映射理论对系统进行了稳定性分析，通过对胞映射作图快速获得平衡胞，利用动态优化原理，找到所有的周期胞和吸引域，达到对系统稳定性分析的目的;利用现场工艺数据进行仿真，结果证明了所提方法的有效性。

数据驱动；建模；粒子群算法；胞映射；稳定性

0 引言

随着科学技术、特别是信息科学技术的快速发展, 冶金、化工、机械、电子、电力、交通运输和物流等企业发生了重大变化。企业的规模越来越大, 生产设备、生产工艺和生产过程越来越复杂[1-3]。 传统方法, 即依据物理化学机理建立精确数学模型, 已变得越来越困难[4-9]。同时相当多的企业每天都在产生大量的生产和过程数据, 这些数据隐含着某些工艺变动或设备运行等信息。理论和工程界迫切需要解决的问题是，如何有效利用这些大量的数据和知识, 在难以建立受控系统较准确机理模型的条件下, 还可实现对生产过程的预报、评价和优化控制。因此, 发展基于数据驱动的控制理论与方法是新时期理论发展与应用的必然要求, 具有极为重要的理论与现实意义[10-12]。

本文针对一类复杂系统进行基于数据驱动方法的建模和控制正是在这一思想理念下产生的。由于这类复杂系统如烧结过程中发生的一系列的物理化学变化,使得其动态特性难以用精确的机理模型进行描述。但通过考察工艺特点，受工艺现场看火师傅根据火焰类型进行温度调节从而使系统工况维持正常运行，进而保证良好的产品质量的思想启发，我们尝试通过已采集的工艺过程参数数据来构建这样一个可以代替人工判断实现复杂系统的自动控制模型。在模型结构确定的基础上，采用改进的量子行为粒子群算法(IQPSO)进行参数辨识。在模型基础上，我们针对相应的自治系统，利用胞映射理论对系统稳定性加以分析。最后，利用采集到的2年的现场实际数据，对改进的算法和胞映射理论加以验证和应用，从而对这一类复杂系统有较为深入了解。

1 复杂系统建模

针对类似烧结机煅烧过程，各种烧结原料按一定比例混合布在台车上，台车一边接受布料、同时向前行进，运行至点火器下，点火，抽风，空气从料层表面吸入，遇到混合料中的燃料发生燃烧反应，在燃料燃烧产生高温的同时发生一系列的物理化学反应，部分混合料颗粒表面发生软化，熔化，产生一定量的液相，并润湿其他未熔化的颗粒，当冷却后，液相将矿粉颗粒粘结成块，这个过程称为烧结。

针对这一类机理难建模系统的复杂特性，通过分析工艺特点，得知烧结质量的好坏取决于烧结终点，因此我们利用历时2年从工业现场采集到靠近烧结终点的烧结台车两边的共8269组6维风箱温度数据，而为了消除采样过程中的干扰和测量误差，因此对数据进行滤波，滤波前后的风箱温度如图2所示。

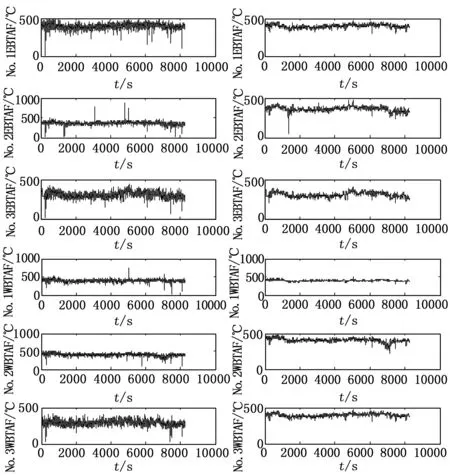
图2 滤波前后时间序列

进一步我们对滤波后的工艺参数数据利用数据驱动和胞映射的建模方法，并进行自相关函数和偏自相关函数的分析，同时通过F检验法对模型阶数和延时进行显著性检验(表1)，构建了如下时间序列受控回归滑动平均(CARMA)胞映射模型结构。

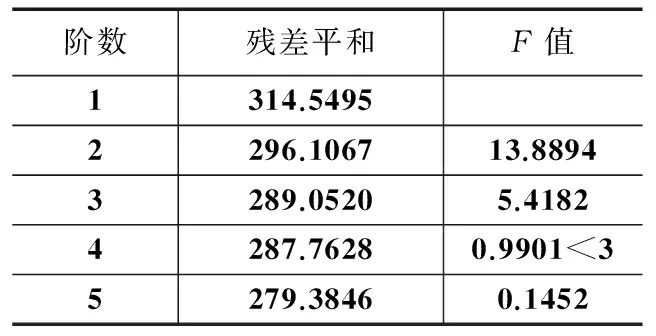
表1 残差平方和检验

y(k+3)=-a2yc(k+2)-a1yc(k+1)-

a0yc(k)+b2u(k+2)+b1u(k+1)

(1)

在模型确定的基础上，我们采用改进的量子行为粒子群优化(IQPSO)与神经元相结合的算法对模型参数进行辨识，该算法是针对粒子群(PSO)算法缺点而提出的。粒子群算法是由美国电气工程师Eberhart博士和社会心理学家Kennedy博士[13]于1995年提出，算法的主要思想源于对鸟类群体行为的研究, 利用生物学家Heppner提出的模型构建粒子群模型和算法。在PSO算法中，搜索域空间中的鸟被作为优化问题的解看待，称为”粒子”。每一个粒子对应着优化问题的一个适应值，优化问题的最优解对应着适应值最好的粒子，适应值根据具体问题而定，比如在控制问题中，往往把具体性能指标作为适应值。在该算法中，粒子的速度决定其飞行方向和距离，粒子通过追寻群体中的最优粒子最终完成解空间的搜索。PSO算法自提出以来，由于其具有计算简单，控制参数少，易于实现等特点，引起了国内外很多学者的关注，开展了一系列研究，在算法的理论分析、性能改进以及应用等方面取得了丰硕成果。

但在PSO算法中，粒子的运动状态由位置和速度确定，随着时间的推移，粒子的运动轨迹是既定的；同时粒子的速度受到一定限制，使得粒子的搜索空间最终是一个有限的并逐渐减小的区域，因此不能覆盖整个可行解空间，所以该算法不能保证全局收敛。

针对这一缺点，根据粒子群的基本收敛性质[14]，我国学者孙俊[15]利用量子力学中的相关理论为基础，设计了一种基于全局水平的参数控制方法，提出了量子行为粒子群优化(QPSO)算法。算法基本原理是通过模拟量子力学中粒子在势场中向势能最低点的移动建立搜索机制。本文在该算法的基础上加以改进，并将之用于我们构建的非线性系统的参数辨识。改进的基本思想是通过增加粒子的多样性，使得算法在前期具有更好的全局探索能力，算法后期，在基本确定待辨识参数的最优值区域的基础上，为提高辨识精度，将搜索到的最优值传递给神经元作为初始权值，利用神经元增强算法的局部开发能力。具体的改进算法如下：

1)确定辨识参数个数，数据长度以及参数初始化。

2)通过如下公式计算群体中每一个粒子的适应度。

3)判断是否收敛或达到最大迭代次数。

4)根据如下改进公式进行等概率的进化粒子。

Xi,j(t+1)=Xi,j(t)±α·|Cj(t)-Xi,j(t)|·ln[1/ui,j(t)]

Xi,j(t+1)=pi,j(k)±α·|pi,j(t)-Xi,j(t)|·ln[1/ui,j(t)]

其中：

ui,j(t)～U(0,1)φj(t)～U(0,1)

Pi(t)=[Pi,1(t),Pi,2(t),...Pi,N(t)]表示个体最好位置。它由下式确定:

(2)

Xi(t)=[Xi,1(t),Xi,2(t),...Xi,N(t)]表示在t时刻第i个粒子的位置，其中i=1,2,..M.G(t)=[G1(t),G2(t),...GN(t)]表示群体的全局最好位置，且G(t)=Pg(t)，g为处于全局最好位置的粒子的下标，g∈{1,2,...M}。群体的全局最好位置由如式(3)、(4)确定：

(3)

G(t)=Pg(t)

(4)

5)重复步骤2)～步骤4)共M次。

6)经过M次学习后将当前最优值传给单神经元，按下列公式对最优解进行局部精确搜索。

(5)

(6)

其中:i=1,...,an+bn,η为学习率。wk={ai(i=1,...an),bi(i=1,...bn)}

[X1,...Xn,...Xan+bn]=[Y(k-1),...Y(k-an),...

U(k-1),...U(k-bn)]

an=3,bn=2

7)转至步骤3)。

8)输出辨识结果，即参数a2,a1,a0,b2,b1的值给系统。

2 模型的稳定性分析

系统的稳定性是系统的固有属性，线性系统由系统的结构和参数决定，与系统的初始条件和外界扰动的大小无关。而非线性系统的稳定性则与初始条件与外界扰动的大小有关。一个系统能够正常工作的前提条件是系统必须是稳定的。在此，针对我们所构建的模型(1)特点，我们选用胞映射为工具讨论系统的稳定性。胞映射的理论基础是马尔科夫链理论、庞加莱点映射原理和相空间重构原理[16-17],它是目前处理和研究时间序列问题，尤其是非线性动力系统全局性能问题的成功方法之一。胞映射方法最先在20世纪80年代初由Hsu[16]提出，方法以其快速，准确和适用范围广等特点很快成为研究的热点，而被很多研究者所关注。它的基本思想是将动力系统状态空间离散化形成许多小的几何体(胞)，全部胞组成的集合形成胞空间。通过划分将动力系统状态空间转化为胞空间后，动力系统中状态的转移就对应为胞之间的转移。进而通过对胞之间转移关系的研究完成对原动力系统的相应研究。这就是胞映射方法的基本思想。胞映射的实现方式是通过构造局部的转移矩阵，以迭代算法进行长时间演化，实际上是用多周期运动来逼近所要描述的非线性运动，最终得到系统状态变量在研究区域的极限概率分布。胞映射的突出特点是只要计算内存容量和速度允许，对非线性动力学系统能够以任意尺度来划分胞元并进行胞映射全局分析[18-21]。通过胞映射分析系统的稳定性，为进一步设计控制器作准备。

针对本文所提的模型特点，用已知输出胞和对应时刻的输入，预测未来系统输出所在胞，胞划分的依据是通过聚类算法得到的，而不同于以往的对状态空间等分划分。由于涉及到依赖未来系统输出寻找其对应的胞，进而通过其胞标号作为反馈信息找到所对应的胞中心从而代入模型(1)得到下一时刻的系统输出胞，因此在此构建的模型不同于以往的线性CARMA模型。针对这种非线性的胞模型特点，我们利用胞映射具有处理非线性系统稳定性的优势特点，优势在于平衡胞的确定和其相应的吸引域的确定比较容易。通过转化为其对应的状态空间模型进而构建胞映射，通过寻找平衡胞以及搜索到达以平衡胞为目标胞的吸引域，对上述特点的系统开展稳定性分析。首先对上述得到的离散时间模型，通过[12]，转化为如下的状态空间胞映射模型。

yc(k)=x1c(k)

通过考察胞空间中每一个胞，在系统对应的自治模型映射下的像胞，得到所有的胞对。对于这些胞对，找到所有的平衡胞，搜索以平衡胞为目标胞，到达目标胞的所有路径。路径上的所有胞构成了吸引域，对应于系统的稳定域。利用动态规划的方法，通过寻找到达以平衡胞为目标胞的所有路径，从而将状态空间中的所有胞进行分类，分类后的胞与稳定性的对应关系如下：

1)平衡胞。对一简单胞映射C，如果胞元素Ze满足：

Ze=C(Ze)

则称Ze为系统的平衡胞。由于系统的稳定性是指：处于平衡点的系统经扰动后，偏离平衡位置，在扰动消失后，系统最终回到平衡点。考察系统的平衡点，对应胞空间中的平衡胞，因此需要对所有的胞对。找到平衡胞，并将之作为在系统稳定性分析中的目标胞，所有目标胞构成目标胞集。从此胞集出发搜索到达此胞集的所有路径，从而确定系统相应的的稳定域。

2)简单胞映射。对每个胞，经过胞映射后，对应的像胞只有一个，该映射的含义是，从原胞到像胞的映射关系是确定的。这种胞映射的算法简单，也使得利用此方法对分析系统的全局性能很有效。但对于复杂系统，利用此方法所需要的胞数量很大。以此简单胞映射为基础，在以后的研究中，要考虑利用广义胞映射、图胞和马尔科夫链理论为基础进一步分析系统的稳定性。

2)周期运动和周期胞。设Cm为映射C进行m次映射，若k个不同胞:Z*(j)(j=1,2,…k)的一个序列满足：

Z*(m+1)=Cm(Z*(1))

m=1,2,…k-1

Z*(1)=Ck(Z*(1))

则说该序列构成一个周期为k的周期运动，简称P-K运动。序列中的每一胞Z*(j)(j=1,2,…k)称为周期为k的周期胞，简称P-K胞。周期胞对应于系统的周期运动。在非线性系统的分析中，实质是用周期胞的周期运动来逼近系统的动态轨迹。

3)暂态胞和吸引域(渐近稳定域)。经过有限次映射并最终到达周期胞的那种非周期胞称之为暂态胞。如果r是一个使胞Z的r次映射成为一个P-K运动的P-K胞Z*(j)，即Cr(Z)=Z*(j)，则称Z距离周期运动有r步远。所有距离周期运动有r步远或者小于r步远的暂态胞的集合叫做周期运动的r步吸引域。而P-K运动的吸引域则是当r→∞时所有这种吸引域的总和。在本文中，我们要做的就是搜索所有能到达以周期为1的平衡胞为目标胞的暂态胞。所有的这些暂态胞集构成了系统的渐进稳定域。

因此，可通过胞映射的搜索对如图3状态胞进行分类，通过考察平衡胞，周期胞以及吸引域达到分析系统稳定性的目的。

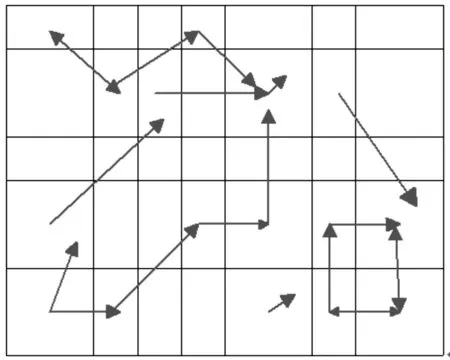
图3 胞映射图

3 数值仿真

利用第1节改进的量子行为粒子群优化与神经元相结合的算法对构建的模型(1)，通过采集的历时两年的安阳烧结机的烧结台车上靠近烧结终点的东西风箱温度以及点火温度进行仿真实验，并利用第2节以胞映射为主要工具对模型相应的自治系统进行稳定性分析。IQPSO算法的各参数设定如下：辨识参数个数为N=5个，首先从最小二乘法中将参数的范围确定，a2,a1,a0,b2,b1∈[-2,2]按数据长度为M=525规模随机初始化5维粒子，参数范围均为[-2，2]，Q=1 000，α=0.8。利用上述第二节的改进算法，得到如下(图4，图5)的辨识结果。图4表示原始时间序列，QPSO辨识得到的参数对应的时间序列以及改进的的辨识参数对应的时间序列。图5为改进前后得到的辨识参数对应的误差时间序列。无论是从图中定性观察，还是从得到的数据定量计算，都可以得出改进的算法是有效的这样的结论。

最后，经辨识得到的模型为:

y(k+3)-0.4231yc(k+2)-0.1430yc(k+1)-
0.1445yc(k)=-0.0591u(k+2)+0.0188u(k+1)

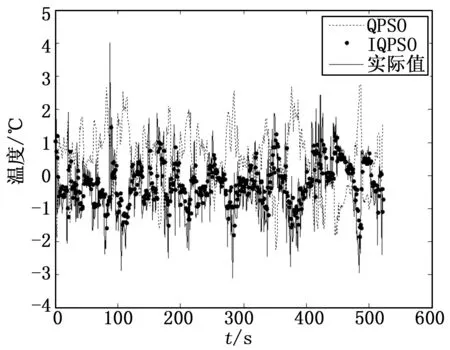
图4 改进前后辨识参数对应的以及实际时间序列

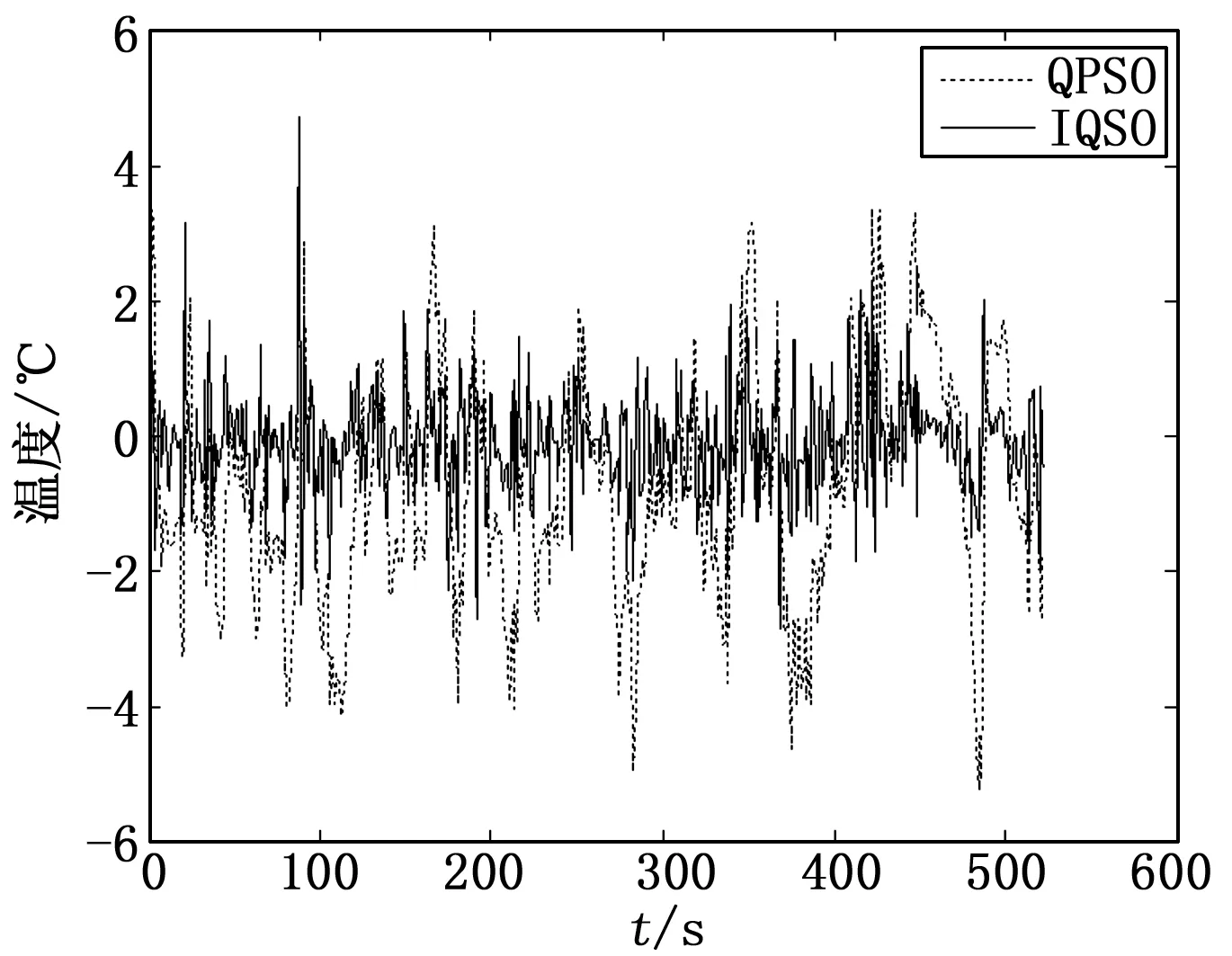
图5 改进前后辨识参数对应的误差时间序列

通过差分方程向离散时间状态空间模型的转换，转换后的状态空间模型为:

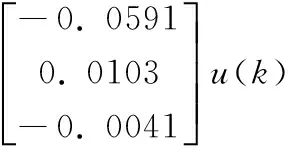
y(k)=x(k)

要讨论其系统的稳定性，则需要令u(k)=0考察其对应的自治系统。通过对胞空间中所有胞经过胞映射得到像胞，与其组成的胞映射对进行搜索算法，利用动态规划最优原理确定系统的稳定域。首先对状态空间进行胞划分，由差分方程的输出和点火温度的输入确定最终的状态空间每一维的范围，即对[-5 5]*[-5 5]*[-5 5]均匀划分为10*10*10=1 000个胞。胞的划分依据对输出工况空间通过聚类反映工况特点的性质得到的。相应地，每一维对应的胞中心如下图6。图7表明对划分后的每一个胞号作为横坐标通过状态空间模型得到的像胞号作为纵坐标得到的胞映射图形。

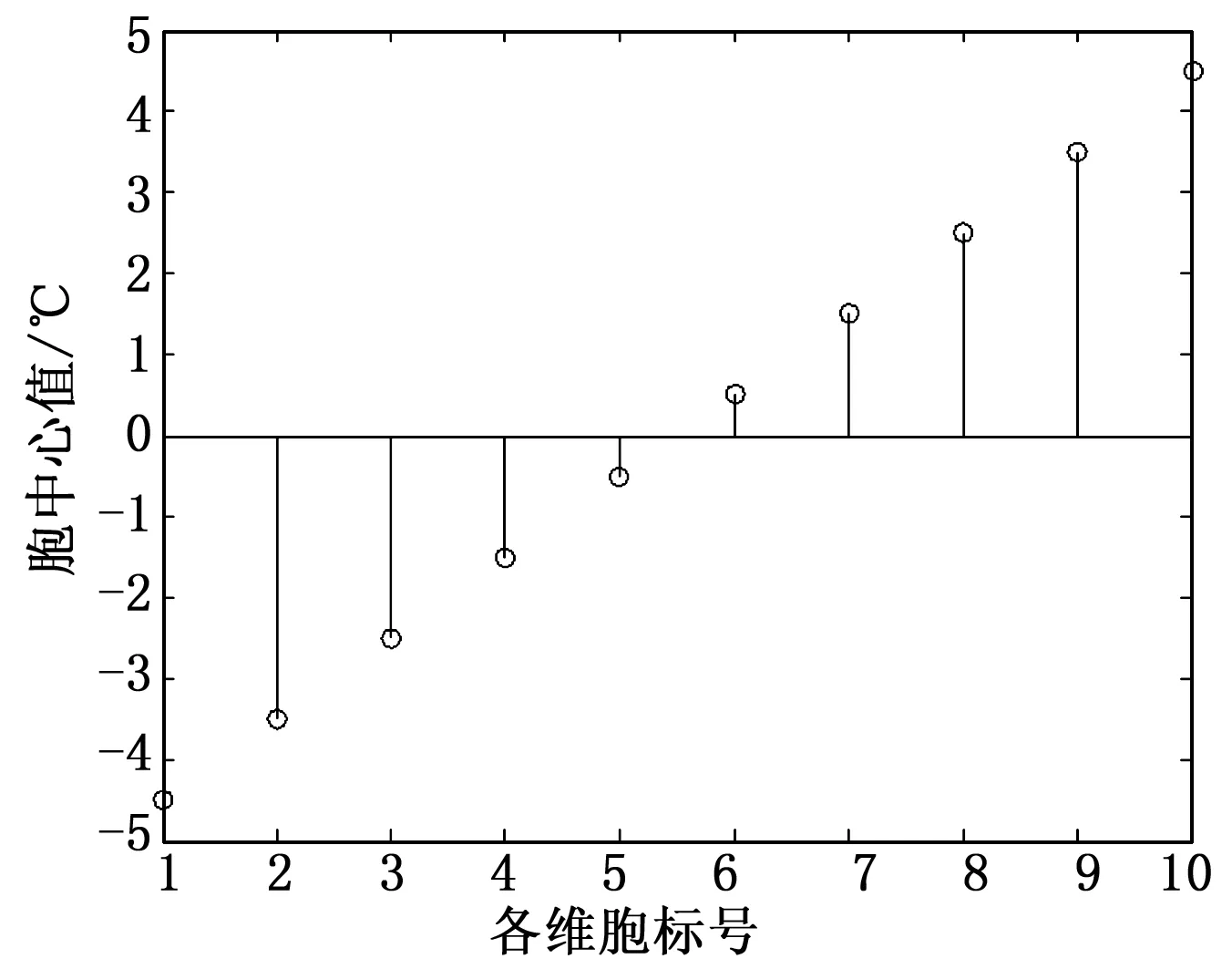
图6 各维划分10个胞时所对应的胞中心

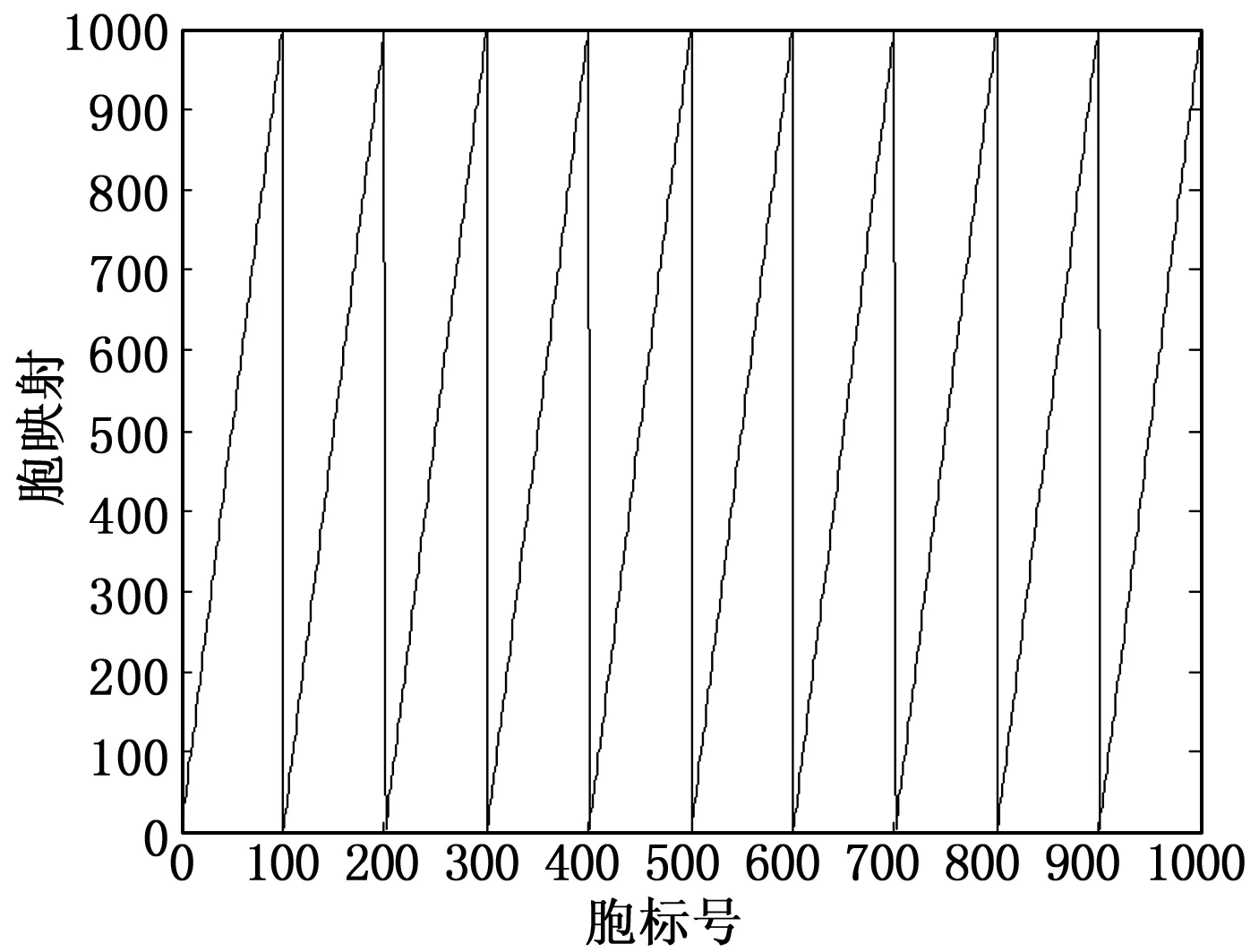
图7 各维划分10个胞时对应胞映射

将胞映射的对应关系绘制成如图7，更能直观地看出系统的动态特性，并且能从对应的胞映射表中得到平衡胞，即原胞和像胞为相同胞。同时从图8中也可以得到平衡胞，即只要将图7中胞映射图与对角线引出的直线相交，相交位置的胞即为平衡胞。例如，将原点所在胞[5,5,5]和[6,6,6]胞标号为445和556的平衡胞作为目标胞，找到目标胞的所有吸引域即为系统对应此平衡胞的稳定域。

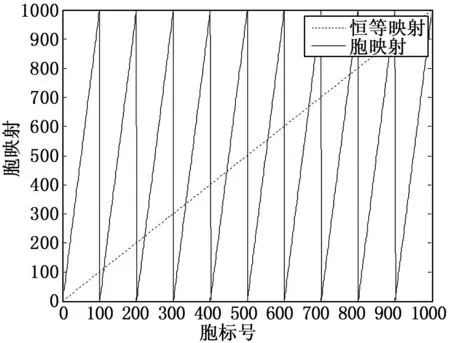
图8 平衡胞

从图8可以看出相交的点对应的胞均为平衡胞，但结合胞映射表进行搜索，得知并不是所有平衡胞都存在吸引域，不存在吸引域的平衡胞对应于着系统的不稳定平衡点，这和系统存在不稳定的平衡点理论是相符的。除稳定的平衡胞，这类胞也称为可达的平衡胞，和其对应的吸引域外，胞空间中其余平衡胞和非平衡胞对应于状态空间中的不稳定区域。利用matlab进行编程，进一步得到稳定平衡胞和其吸引域对应的胞的个数为616，占整个胞数的74/125，稳定平衡胞和其吸引域对应于状态空间中的稳定域。因此，可以看出，以胞映射为工具可以实现对这类复杂系统的稳定性分析，并且分析过程得到简化。

4 结束语

针对如烧结机等一类复杂系统难建模的特点，本文利用数据驱动的建模方法，通过采集2年的工艺参数数据，建立受控回归滑动平均(CARMA)胞映射模型。在确定模型结构的基础上，利用改进的量子行为粒子群与神经元结构相结合的算法，对模型进行参数辨识。进一步，将离散时间的CARMA模型转为状态空间模型。在状态空间中进行胞划分，所有胞的集合构成胞空间。利用简单胞映射，对胞空间中的每一个胞以胞中心作代表经过状态空间模型得到像胞，构建胞映射。利用平衡胞定义，找到所有的平衡胞。以平衡胞为目标胞搜索所有到达平衡胞的路径，对应系统的稳定域。实现以胞映射理论讨论此类复杂系统的稳定性目的。最后，给出了仿真实例，实验证明此方法是可行的，因此为这类复杂系统的动态特性分析提供了一条思路。在此基础上，可进一步开展针对控制器的设计工作。

[1]HuangLG.Influenceofsinteringtemperatureoncrystallinephasessynthesizedfromfinesiliconpower[J].Chinaceramics,2007,43(9):23-25.

[2]KangGZ,JiaBG,WangLMetal.Theuseofrotarykilninferroalloysproduction[J].Ferro-alloys,2011,218(3).

[3] 蔡 健,王百红,梁慧强,等.电解铝生产电解电容器负极箔的关键技术[J].轻合金加工技术.2004,32(9):17-21.

[4]AdamyJ.A.flemming.softvariable-structurecontrols:asurvey[J].Automatica, 2004,40: 1821-1844.

[5]KonstantinosK,JohnL.ModelingandanalysisofDNAreplication[J].Automatica, 2011,47, 1156-1164.

[6]HenryY,GranthamK,NelsonH.Performancevaluationformotif-basedpatternedtexturedefectdetection[J].IEEETransactionsonAutomationScienceandEngineering, 2010, 7(1):58-72.

[7]StachW,WitoldP,LukaszA.Learningoffuzzycognitivemapsusingdensityestimate[J].IEEETransactionsonsystems,man,Cybernetics-partB:cybernetics, 2012, 42(3): 900-912.

[8]HouZS,JinST.Anoveldata-drivencontrolapproachforaclassofdiscrete-timenonlinearsystems[J].IEEEtransactionsoncontrolsystemstechnology, 2011, 19(6):1549-1558.

[9]BeghiA,BrignoliR,CecchinatoL,etal.Data-drivenfaultdetectionanddiagnosisforHVACwaterchillers[J].ControlEngineeringPractice,2016,53(8):79-91.

[10]WangJS,YangGH.Data-drivenoutput-feedbackfault-tolerantcontrolforunknowndynamicsystemswithfaultschangingsystemdynamics[J].JournalofProcessControl,2016,43(7):10-23.

[11]WangYJ,YangD,ZhangX,etal.Probabilitybasedremainingcapacityestimationusingdata-drivenandneuralnetworkmodel[J].Journalofpowersources,2016,315(5):199-208.

[12]LiuBao.ModernControlTheory[M].Beijing:ChinaMachinePress,2000.

[13]KenneyJ,EberhartRC.Particleswarmoptimization[C].ProceedingofIEEEInternationalConferenceonNeuralNetworks,1995,1942-1948.

[14]ClercM,KennedyJ.Theparticleswarm:explosion,stabilityandconvergencyamulti-dimensionalcomplexspace[J].IEEETransactionsonEvolutionaryComputation, 2002，6:58-73.

[15]SunJ,XuWB,FengB,Aglobalsearchstrategyofquantum-behavedparticleswarmoptimization[c].In:ProceedingsofIEEEConferenceonCyberneticsandIntelligentSystems,Singapore,2004, 111-116.

[16]HsuCS.Ageneralizedtheoryofcell-to-cellmappingfornonlineardynamicalsystems[J].ASMEJ.Appl.Mech, 1981,48:634-842.

[17]HengL,LieY,XieY.ThecontinuousPoincare-likecellmappingmethodanditsapplicationtononlineardynamicsanalysisofabearing-rotorsystem[J].TribologyInternational,1998,31(7):369-375.

[18]SunJQ,HsuCS.Globalanalysisofnonlineardynamicalsystemswithfuzzyuncertaintiesbythecellmappingmethod[J].Comput.Meth.Appl.Mech.Eng.,1990,83(2):109-120.

[19]SunJQ,HsuCS.Thegeneralizedcellmappingmethodinnonlinearrandomvibrationbaseduponshort-timeGaussianapproximation[J].J.Appl.Mech.,1990,57:1018-1025.

[20]HongL,XuJX.Crisesandchaotictransientsstudiedbythegeneralizedcellmappingdigraphmethod[J].Phys.Lett.A,1999,262:361-375.

[21]HongL,XuJX.Discontinuousbifurcationsofchaoticattractorsinforcedoscillatorsbygeneralizedcellmappingdigraph(GCMD)method[J].Int.J.BifurcatChaos,2001,11:723-736.

Dynamical Performance Analysis for a Class of Complex Systems Based on Data Driven

Guo Lingli1,2,Wang Mushu1，Wang Ye1

(1.School of Automation and Electrical Engineering, University of Science &Technology Beijing, Beijing 100083,China; 2.Department of Mathematics Changzhi College, Changzhi 046011,China)

A model and the stability analysis are proposed for a class of dynamical systems which is difficult in modeling due to the complex physicochemical change by data-driven method. A CARMA cell mapping model is established, whose parameters are identificated by quantum-behaved particle swarm optimization. To avoid the premature convergence of the IQPSO algorithm, the particles position are updated and accurate search capacity is enhanced by applying the neural networks that train the optimal value as the initial weighted value. Based on the model, the stability performance is analyzed by cell mapping theory and dynamic optimization principle, which is helpful to find the whole periodic cell and attractive domain. Simulation studies are included to demonstrate the effectiveness of the proposed approach.

data driven; modeling; particle swarm algorithm; parameter identification; cell mapping; stability

2016-12-12；

2017-01-19。

国家自然科学基金(61175122)。

郭玲利(1978-)，女，山西长治人，博士研究生，讲师，主要从事控制科学与工程方向的研究。

1671-4598(2017)04-0220-05

10.16526/j.cnki.11-4762/tp.2017.04.060

TP273

A