平面域Delaunay三角网点定位算法研究综述

刘琴琴

（陕西师范大学 计算机科学学院，陕西 西安710062）

平面域Delaunay三角网点定位算法研究综述

刘琴琴

（陕西师范大学 计算机科学学院，陕西 西安710062）

不规则三角网常用于地形的可视化，其生成算法一直是国内研究热点。Delaunay三角剖分算法是构建不规则三角网的主要算法。讨论了平面域离散点生成Delaunay三角网算法的研究现状，其中逐点插入法中影响构网效率的关键因素是任意插入点定位的速度。总结了目前国内主流的点定位算法，对国内该领域现有文献研究存在的主要问题作了详细分析，并展望了未来可能的研究走向，以期为国内Delaunay三角网生成算法研究提供理论与方法上的指导意见。

Delaunay；不规则三角网；逐点插入法；点定位

在地理信息系统中，数字高程模型最基本和最重要的模型是不规则三角网 （Triangulated Irregular Network，TIN）模型。不规则三角网是由不规则的离散点生成互不交叉、互不重叠又相互邻接的连续三角形来拟合地形的[1-2]。由于Delaunay三角网[3]具有唯一性、空外接圆和最大的最小内角等性质，所以在一般情况下，Delaunay三角网被公认为是所有构网规则中最优的[4]，因此被广泛应用。

Delaunay三角网生成算法经过20多年的研究已取得了丰富的研究成果，按照构网过程的不同，主要可分为三角网生长法[5]、分治算法[6]和逐点插入法[7]，采用后两种以及两种结合算法较多。

三角网生长法构网步骤相对简单，时间效率较差，平均时间复杂度为O（n2）[8]，现应用很少。

分治算法构建三角网思路简单，运行速度较快，构网费时与离散点数基本成正比[9]，其缺点是需占用大量的内存来存储空间，相对复杂。

逐点插入法构网原理简单，内存占用少，容易实现，但时间复杂度差，运行速度慢，主要影响因素为点在三角形中的定位和三角网的优化。近年来，一些学者致力于点定位算法的研究，并取得了一定的理论成果。文中依托CNKI中国知网，对Delaunay三角网生成算法的相关中文文献进行检索和整理，总结和讨论了任意点定位的改进算法，同时对国内该领域现有文献的研究局限作了详细分析，并展望其未来可能的研究走向。

1 逐点插入法

逐点插入法于1977年由Lason提出，后来Lee和 Schachlter、Bowyer、Watson、Sloan以及 Tsai等学者对其进行了改进，具体过程如下：

1）定义一个初始多边形包含所有离散点，在初始多边形中构建初始三角网；

2）数据点的插入：从离散点中选取一点P，定位该点所在的三角形，连接点P与包含该点的三角形的3个顶点，形成新三角形；

3）优化三角形[10]；

4）迭代2）、3）步骤，直至插入完所有离散点。

逐点插入法在建立初始三角网后，将点插入到初始三角网中时，需要查找包含该点的三角形，即点定位[11]。随着点的插入，点数增加，三角形数量也成倍增加，查找该点所在的三角形的过程非常费时，执行效率低，算法平均时间复杂度为O（n log n），在最坏情况下时间复杂度为O（n2）[8]。由此可见，定位点所在的三角形是影响逐点插入法构网效率的一个关键步骤。

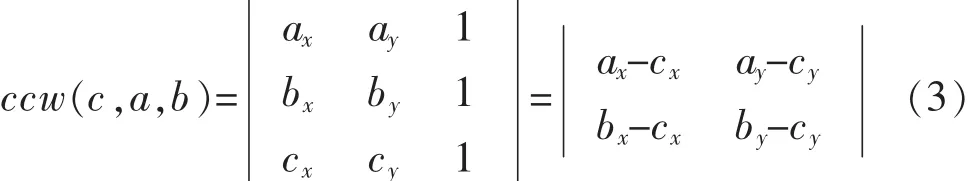
2 平面域Delaunay三角网点定位算法

为了提高逐点插入法构建Delaunay三角网的效率，国内很多学者已提出了相应的点定位算法。

2.1 基于面积坐标定位算法

定位点所在的三角形和判断下一个三角形的算法比较多。根据有限元理论，刘学军等人提出利用三角形面积坐标和三角网的拓扑关系来定位[12-13]。假设三角形 3个顶点坐标为 V1（x1，y1）、V2（x2，y2）、V3（x3，y3），面积为S，任意插入点P（xp，yp）与三角形构成的矢量面积分别为S1、S2、S3，面积坐标分别为L1、L2、L3，三角形顶点按逆时针排列，则：

若3个面积坐标均大于0，则点P位于三角形内；若至少有一个面积坐标小于0，则点P位于三角形外；若有面积坐标为0，则点P位于三角形的边上（不考虑点P与三角形顶点重合的特殊情况）。通过该方法可很快定位出点所在的三角形，计算效率较高，缺点是搜索路径不唯一，当出现两边的面积坐标S1、S3都为负值时，搜索路径不唯一。

2.2 点线关系方向定位算法

为了解决搜索定位路径唯一性问题，宋占峰等人提出了方向搜索法，基本思想为：从首三角形开始，利用点在直线边侧的检测（CCW检测），需要判断插入点P和三角形的重心G是否相对于三角形的某一边位于异侧，若点P与重心G相对于三角形的3条边都位于同侧，则点P在三角形中，若点P与重心G相对于三角形的某一边异侧，则以该边为公共边的相邻三角形就是下一个搜索三角形[14]。点与三角形某条边的关系可用公式（3）判断：若ccw（c，a，b）大于0，则点c在向量ab的左侧；若ccw（c，a，b）小于0，则点c在向量ab的右侧；若ccw（c，a，b）等于0时，则点c在向量ab上。

宋占峰等人[14]采用方向搜索法可快速定位点所在的三角形，缺点是该方法在特殊情况下也会出现搜索路径不唯一，虽然不影响最后的效果，但明显增加了运算量，效率较低。刘少华等人[15]提出点边方向定位法，根据点和有向线段的正负性来判断点是否在三角形中，计算效率较高，但搜索方向不唯一。李小秋等人[16]将上一个插入三角形作为下一插入点的搜索初始三角形，使用方向搜索法定位点所在的三角形，在实际测量数据构建三角网的速度可达每秒15万个点，在效率上能满足工程设计需要；文献[17]则将三角形顶点按顺时针排列，将新生成的三角形作为初始三角形并采用方向搜索法定位，可保持较高的生成效率；Jian Hui-xi[18]也采用方向搜索法定位。

为了进一步解决搜索定位路径不唯一问题，很多学者在此基础上提出了改进算法，如徐道柱等人[19]在此基础上增加了一个条件，在判断点P和三角形的重心G是否相对于三角形的某一边位于异侧时，判断重心G与点P的连线GP与三角形的边是否相交，验证表明算法的效率可提高4倍多；杨小运等人[20]提出“基于三角形方向搜索”的方法，通过判断三角形与插入点与三角形顶点形成的三角形的方向是否相同来定位，只需简单的数值比较运算可判断三角形的方向，有效缩短了构网过程中定位点的时间；蒲浩等人提出最速方向定位法[21]，将三角形重心G与点P连线GP作为方向线，若三角形不包含点P，则下个搜索三角形则为与方向线GP相交边的相邻三角形，如图1所示，刘云等人[22]也用此方法来定位点所在的三角形。这些方法都不同程度的提高了点定位三角形的效率，解决了搜索路径不唯一性。其中，最速方向定位法虽然路径唯一，但不是最短路径，没有考虑方向线GP与三角形顶点、边重合的情况，当遇上特殊情况时会出现死循环（如图2所示）。

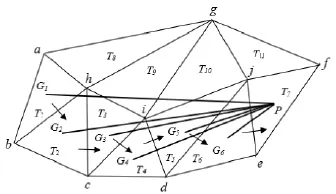
图1 最速方向定位法

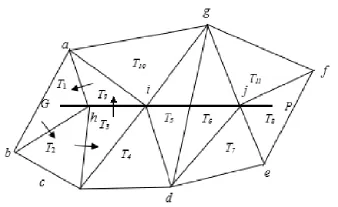
图2 点与线、三角形之间的关系

针对最速方向定位法中存在的不足，刘少华等人[15]还结合最速方向定位法，规定若方向线GP经过三角形顶点时，则以这个顶点为中心逆时针搜索三角形，判断方向线GP与三角形边的关系，若三角形的某一边与方向线GP重合，则以这条边的另一个顶点为中心逆时针搜索三角形，重复以上步骤，解决了方向线GP与三角形顶点、边重合的情况，定位路径唯一，保证了算法的稳健性和高效性，但也不是最短路径，也没有利用点与三角形的拓扑关系，计算重心的次数也较多。针对上述算法中的不足，邹永贵等人[23]充分考虑了点与三角形的拓扑关系，改进了算法，减少了重心计算次数，运算步骤也减少，搜索路径唯一，通过验证表明，在相同的离散点数据条件下，文献[15]计算了7次重心、7次相交边，而此算法只计算了2次重心、2次相交边，耗时明显小于文献[15]，提高了定位效率和构网速度。张咏等人结合三角形面积坐标定位法、重心方向搜索法和点边方向定位法[15]这三种方法，提出融和算法[24-25]，如图 3所示，在相同的离散点条件下，融合算法比基于面积坐标的定位算法搜索的三角形减少了，构网效率提高了。融合算法不仅定位路径惟一，还是最短路径，构网效率高，在健壮性和效率上达到了有效平衡，但由于没有引入格网索引，整体定位效率不高。

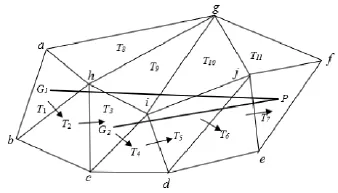
图3 融合算法

2.3 格网索引法

对离散点分块管理是快速定位点所在三角形的一个重要方法，该方法通过缩小查找范围而使点定位效率提高。定位点所在的三角形，先将离散数据点划分成矩形网格，将离散点的编号依照点的坐标存储到对应的网格中，通过计算三角形的重心坐标即可判断出所在的网格，然后通过网格中记录的三角形进行判断。徐旭等人采用网格分块的方法对构网离散点和已生成的三角网建立索引来提高点在三角网中的定位效率[26]，大大缩小了搜索范围，提高了点定位速度。

很多研究学者也采用格网索引法来定位点所在的三角形。如蒋瑜等人[27]将离散点总体上看成随机均匀分布，采用格网索引法来定位，但实际测量数据并非随机分布，常常存在一些约束关系，不够通用；赵岩等人[28]选择适当的格网大小对三角网进行存储从而减小点定位时遍历次数；李小丽等人[29]将数据按线性四叉树方式划分成若干格网来构建三角网；文献[30-31]则采用自适应格网划分来构建Delaunny三角网。也有学者提出结合格网索引法和点线关系方向定位法的算法，如姜志伟等人[32]提出基于格网索引和方向法搜索的三角网生成算法，该算法构网效率比一般插入法高，构网效率和点的个数几乎成线性关系，可利用该算法快速找到约束线段的影响三角形；王涛等人[33]利用建立的格网索引确定已知顶点后，由顶点与定位点组成方向线，搜索判断与方向线相交的边所在的三角形是否包含定位点，算法搜索路径惟一，但计算步骤较融和算法多。

3 存在的问题与研究趋势

3.1 存在的问题

1）研究注重提出新算法，缺少算法的实用性分析。如算法能适应多大的数据量、适用何种数据形式以及能处理的数据复杂度等等，同时，算法效率分析也很重要，目前很多算法提出却实用性较少。

2）格网索引法可大大缩小搜索范围，提高了点定位三角形的效率，但在对构网过程中的三角形格网分块时，若单个格网过大，则处理格网中的三角形需要大量的耗时，若单个格网过小，则格网数量会很大，许多格网会出现无点的情况，对三角网在格网中的存储、内存占用等都有影响。在大多数情况下，格网索引法可以使初始三角形与目标三角形距离很近，但少数情况下，距离却很远，从初始三角形定位点所在的三角形需查找的三角形的数目很多，耗费了大量的时间。

3）三维领域的应用较少。文献虽然提出了一些关于Delaunay三角网的地形三维可视化的方法，但是大部分都是基于二维空间的，但二维空间是无法直观地表述地形形态的，在三维领域中的应用研究较少。

3.2 研究趋势

Delaunay三角网生成算法一直是国内学者研究的热点。目前，随着Delaunay三角网的应用需求以及领域逐渐扩大，特别是为了解决大规模三维地形可视化，对三角网的构网效率和稳定性要求更高，因此有必要对Delaunay三角剖分算法继续深入的研究。文中总结了平面域Delaunay三角网任意点定位算法的原理和步骤，虽已突破以往算法，在数据结构和构网效率方面取得较好性能，但还有一定的改进空间。结合本文的研究，本人认为今后该算法的研究方向主要有以下几个方面：

1）算法的改进。Delaunay三角网算法常被用来处理海量数据，算法的效率特别重要。Delaunay三角网任意点定位算法各有优缺点，将多种算法合理的结合起来，相互补充，综合应用，从而提高Delaunay三角网的构网效率成为目前的研究热点。在对构网过程中的三角形格网分块时，格网的大小很重要，过大、过小都会影响算法的效率，因此需要对比分析，看怎么样划分网格才能使构网效率较高，这是我下一步需要做的工作。

2）研究提出了很多算法，各有其适用范围和条件，当面对一个具体的地形时，选用一种或多种适合的算法非常重要。因此，需要在对各种算法进行详细分析之后选择相应的算法处理。

3）三维领域的应用研究。文中论述的Delaunay三角网是基于二维空间的，算法已趋于成熟，但二维空间是无法直观地表述地形形态的，随着三维地形可视化的发展需要，还需进一步研究其在三维领域中的应用。

4 结束语

随着地理信息系统的发展，不规则三角网作为其关键技术，在三维地形可视化中已广泛应用，在Delaunay三角网生成算法上已取得众多学术成果。文中讨论了平面域离散点构建Delaunay三角网算法的研究现状，总结了当前国内主流的点定位算法，分别从基于面积坐标定位算法、点线关系定位算法和格网索引法3个方面介绍了它们的原理和步骤，但一些关键问题还未能完全解决，今后还需继续研究。随着研究的深入，该领域的研究将会进一步得到改善，从而更好地发挥应用价值。

[1]魏向辉，夏春林，鲁庆伟.一种基于凸包的Delaunay三角网算法设计[J].测绘科学，2010（5）: 152-153．

[2]李志林，朱庆.数字高程模型[M].2版.武汉:武汉大学出版社，2003.

[3]李凤霞，刘咏梅，王晓哲，等.一种基于映射法的散乱点云Delaunay三角剖分算法[J].计算机应用研究，2014（3）:950-953.

[4]武晓波，王世新，肖春生.Delaunay三角网的生成算法研究[J].测绘学报，1999（1）:28-35.

[5]吴佳奇，徐爱功.Delaunay三角网生长法的一种改进方法[J].测绘科学，2012（2）:103-104.

[6]Shamos M，Hoey D.Closest point problems[C]// Proceeding of the 16th Annual IEEE Symposium on Foundation of Computer Science，1975:151-162.

[7]Liu Jian-fei， Yan Jin-hui，S.H.Lo.A new insertion sequence for incremental Delaunay triangulation[J].Acta Mechanica Sinica，2013（1）: 99-109.

[8]栾晓岩.一种TIN生成算法及其三维显示[J].海洋测绘，2004（5）:39-41.

[9]向传杰，朱玉文.一种高效的Delaunay三角网合并生成技术[J].计算机应用，2002（11）:34-36.

[10]俞亚磊，罗永龙，郭良敏，等．Delaunay三角网中任意约束线段嵌入的算法 [J].测绘科学，2013，38（4）:61-63.

[11]陈定造，林奕新，刘东峰.三维Delaunay三角剖分快速点定位算法研究 [J].计算机工程与科学，2009（5）:79-81.

[12]刘学军，符锌砂，赵建三.三角网数字地面模型快速构建算法研究[J].中国公路学报，2000（2）:31-36.

[13]汤国安，刘学军，闾国年.数字高程模型及地学分析的原理与方法[M].北京:科学出版社，2005.

[14]宋占峰，蒲浩，詹振炎.基于三角网数字地面模型快速定位算法的研究[J].中国铁道科学，2002（1）: 63-66.

[15]刘少华，吴东胜，罗小龙等.Delaunay三角网中点目标快速定位算法研究 [J].测绘科学，2007（2）: 69-70.

[16]李小秋，许民献，尹志永.Delaunay三角网关键技术探讨[J].测绘工程，2011（6）:61-63，67.

[17]王龙浩，王解先.基于逐点插入法的Delaunay三角网快速生成算法[J].工程勘察，2013（10）:75-79.

[18]Jian Hui Xi.An Improved algorithm based on incremental insertion in delaunay triangulation[J]. Applied Mechanics and Materials，2013:1691-1694.

[19]徐道柱，刘海砚.Delaunay三角网建立的改进算法[J].测绘与空间地理信息，2007（1）:38-41.

[20]杨小运，陈和平，顾进广等.约束Delaunay三角网生成算法的研究与应用[J].计算机工程与设计，2012（5）:1842-1846.

[21]蒲浩，宋占峰，詹振炎.快速构建三角网数字地形模型方法的研究[J].中国铁道科学，2001（6）:100-105.

[22]刘云，夏兴东，黄北生.基于分治算法与逐点插入法的Delaunay三角网建立算法的改进 [J].现代测绘，2010（4）:14-16.

[23]邹永贵，张涛.改进的平面域Delaunay三角网生成算法[J].计算机工程与应用，2013（20）:171-174.

[24]张咏，刘长星，杨瑜华，等.基于融和算法的二维Delaunay三角网任意点定位研究 [J].测绘科学，2010（2）:85-88.

[25]张咏，杨瑜华，董汉军.二维Delaunay三角网的任意点插入算法研究 [J].地理与地理信息科学，2009（4）:45-18.

[26]徐旭，李源，陈学工.一种基于插入法的Delaunay三角网生成算法 [J].电脑与信息技术，2010（4）: 29-31.

[27]蒋瑜，杜斌，卢军，等.基于Delaunay三角网的等值线绘制算法[J].计算机应用研究，2010（1）:101-103.

[28]赵岩，张子平.一种动态构建Delaunay三角网的算法[J].测绘工程，2008（3）:24-27.

[29]李小丽，陈花竹.基于格网划分的Delaunny三角剖分算法研究 [J].计算机与数字工程，2011（7）: 57-59.

[30]许多文.不规则三角网（TIN）的构建及应用[D].赣州：江西理工大学，2010.

[31]胡金星，马照亭，吴焕萍，等.基于格网划分的海量数据Delaunay三角剖分[J].测绘学报，2004（2）: 163-167.

[32]姜志伟，王山东，王伶俐，等.基于格网和方向法索引的Delaunny三角网生成算法 [J].测绘工程，2014，23（2）:57-60.

[33]王涛.地貌信息提取中的结构化问题研究[D].武汉:武汉大学，2005.

Overview of point location algorithm of Delaunay triangulation on plane domain

LIU Qin-qin
（School of Computer Science，Shaanxi Normal University，Xi’an 710062，China）

Triangulated irregular network has been used to visualize the terrain modeling and the generation algorithm has been great concerned.The algorithms of Delaunay triangulation are the main algorithms when establishing TIN.This thesis presents the status of Delaunay triangulation algorithms and reviewed popular triangle location algorithms.Finally，the paper makes an in-depth an anlysis of the limitation of the existing literature and put forward the issues worthy of further discussion.Understanding these may give new insights into the algorithms of Delaunay triangulation and provides the guidance on the theory and method.

Delaunay；triangulation irregular network；incremental insertion；point location

TP391

：A

：1674－6236（2017）01-0047-05

2015-12-18稿件编号：201512196

刘琴琴（1990—），女，山西吕梁人，硕士研究生。研究方向：三维重建。