基于非线性滤波的GLONASS/GPS融合定位方法

姚慧，茅旭初，王俊璞

（上海交通大学 电子信息与电气工程学院，上海 200240）

基于非线性滤波的GLONASS/GPS融合定位方法

姚慧，茅旭初，王俊璞

（上海交通大学 电子信息与电气工程学院，上海 200240）

为了避免对单一卫星导航系统的过分依赖，并且针对在观测条件较差，单一系统无法定位或者定位精度急速下降的情况，提出了一种基于非线性滤波的GLONASS/GPS双系统融合定位的方法。采用扩展卡尔曼滤波（EKF）和平淡卡尔曼滤波（UKF）算法，并引入伪距判别选星策略，削弱观测卫星数量跳变对定位精度的影响，进行双系统融合定位，并针对恶劣环境，选取仰角最高的五颗卫星进行双系统定位。实验结果表明，算法有较高的定位精度和稳定性，尤其在恶劣情况下，单系统卫星数不足时，双系统融合定位更显示其优势。

卫星导航；GLONASS/GPS双系统定位；卡尔曼滤波

目前，全球定位系统GPS的精密单点定位技术已很成熟，能够为全球用户提供高精度的导航定位服务，但卫星可见性受应用环境的影响很大，在观测条件很差时，其可见卫星数、定位精度和可用性都会大幅下降，无法保障定位可靠性，甚至无法进行定位解算[1-5]。GLONASS是第二个可实现全球定位的卫星导航系统。近几年，随着俄罗斯的星座能力恢复计划、GLONASS-K/KM/NG新卫星系统研制等策略的推出，GLONASS系统得到了长足的发展[6-8]。GPS与GLONASS融合定位，可大大提高卫星可用数量，改善卫星几何分布，提高定位的可靠性、精确性及系统的自主完备性，在卫星可视条件不好的情况下，弥补单一系统无法定位的缺陷[9-10]。因此，GPS与GLONASS融合定位具有重要的应用前景。文中提出了一种保障卫星定位可靠性的GPS/GLONASS双系统融合伪距定位模型，并增加根据跳变卫星伪距来删选卫星的策略，采用非线性卡尔曼滤波算法进行定位估计，实现了高精度、高可靠的单机定位。

1 GPS/GLONASS融合定位原理

GPS和 GLONASS都是利用卫星与接收设备之间信号传输时间测距原理来确定地面用户所在的位置[11]，有伪距方程：

式（1）表示接收机计算得到的实际伪距ρi与真实几何距离Ri的关系。式中：Xu、Yu、Zu为接收机方位坐标；Xi、Yi、Zi为不同卫星系统的第颗卫星的方位坐标；δt是接收机相对于定位系统的用户时钟偏差；c为真空中光速；vi是第i号卫星的其余未建模的测量误差的总和，在解算过程中一般设为白噪声。对于GPS和GLONASS双系统定位，有如下伪距方程[12-13]：

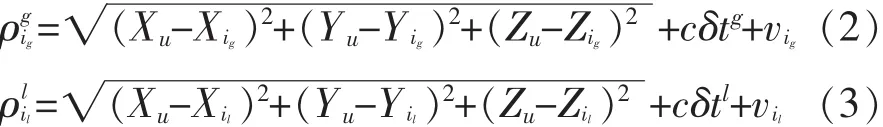
cδtg和δtl分别是接收机相对于GPS和GLONASS系统的用户时钟偏差，GPS和GLONASS系统间钟差记为δtsyst=δtl-δtg。从以上方程可以看出，双系统解算用户位置需要求解5个未知量：Xu、Yu、Zu、δtg和δtb，比单系统多一个系统时间差的未知数。所以必须至少需要5颗卫星才能进行双系统定位解算。

2 GPS/GLONASS融合定位解算方法

2.1 新增卫星的删选策略

由伪距定位原理可知，伪距的观测值对于定位结果有着直接的影响，通过观察发现伪距观测值有时会有较大的偏差，尤其是在某一时刻某颗卫星刚进入到可观测范围时，新增卫星伪距的偏差会造成定位结果出现误差。文中针对新增卫星，根据其伪距是否准确来决定此颗卫星是否为有效的定位卫星。

图1 判别伪距删选卫星流程图

针对新增卫星，如图1所示，通过其它卫星解算用户位置，再反推出新增卫星的正确伪距，与接收机采集的伪距比较，如果差值大于规定阈值，则认为此时新增卫星伪距有较大偏差，该卫星无效。否则，该卫星有效。其中阈值是通过文中定位实验所有有效卫星反算得出的伪距与接收机采集伪距之差来确定的。选择有效卫星最大伪距差值作为该阈值。

2.2 基于非线性滤波的双系统定位模型

目前卫星定位通常采用的线性模型是最小二乘迭代算法ILS。最小二乘法把伪距的测量误差当作白噪声，定位解算快速简单，但精度不高，稳定性不强，在恶劣的定位环境下，鲁棒性也很弱[14]。通过改进噪声模型，引入非线性滤波，可提高定位精度和稳定性。在非线性滤波中，考虑系统模型，即状态模型与测量模型。

2.2.1 状态模型

其中：wci为接收机第i通道的驱动噪声，假设这些噪声为零均值、非相关的随机白噪声，参数φ和φ可由下式得出[11]：

2.2.2 测量模型

由于接收机的位置和速度受多普勒频移影响，所以将多普勒方程加到测量模型中：

系统的测量方程还包括非线性的伪距测量方程，如下：

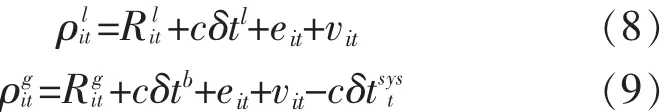
式中：Xit、Yit、Zit为 t时刻第 i颗卫星的位置坐标；δRt为由时钟偏移引起的距离差，ρit为在时刻第颗卫星的伪距；eit为接收机通道i的非白噪声误差；vit为通道i的测量噪声。故当观测到n颗GLONASS卫星和m颗GPS卫星时，系统的测量方程如下：

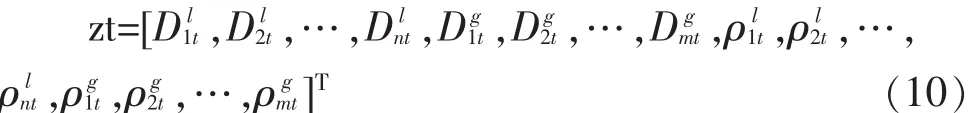
2.3 非线性卡尔曼滤波

卡尔曼滤波最早出现在上世纪60年代，是一种高效的最优化自回归数据处理算法，能够从一系列含噪声的测量中估计系统的状态，已在工程中得到了广泛的应用。UKF和EKF是非线性卡尔曼滤波中应用广泛的两种方法。EKF通过对非线性函数的泰勒展开式进行一阶线性化截断，从而将非线性问题转化为线性问题，在解决非线性问题中得到了广泛的应用。但EKF也存在不足，如在线性化过程中只保留一阶结果，会产生不可忽视的线性化误差；EKF需要进行雅可比估计和求偏微分，在实际应用中有过多的局限性等[15]。UKF是一种用采样策略逼近非线性分布的方法。UKF以UT变换为基础，采用卡尔曼线性滤波框架，采样形式为确定性采样，而非粒子滤波PF的随机采样。UKF采样的粒子点（一般称为Sigma点）的个数很少，具体个数根据所选择的采样策略而定。最常用的是（2n+1）个Sigma点对称采样。UKF的计算量基本与EKF算法相当，但性能优于EKF，并且采用的是确定性采样，从而避免了PF的粒子点退化问题[16]。此外，UKF还有无需对方程求偏微分、无需进行雅可比矩阵的估计等优势。相对于EKF，UKF有着很大的优势。

3 定位实验及结果分析

为了验证文中提出的定位方法的有效性，使用NovAtel公司OEM-628多系统接收机获取卫星原始数据进行实验。采样地点为上海交通大学电院群楼楼顶，天线无遮挡，采样频率1Hz，采样时长2500s。定位实验以OEM-628在同一位置连续24小时定位的平均值为基准。

3.1 非线性滤波定位实验

实验中，GLONASS和GPS接收到的卫星数变化情况如图2所示。GLONASS在454秒和555秒处有新增卫星；1 617~2 362 s期间GPS的卫星数在9和10之间跳动。首先采用最小二乘法进行两次定位解算：得到不使用伪距判别删选卫星策略的ILS1和用策略的ILS2，结果分别如图3（a）、（b）所示。结果表明，若不采用删选卫星策略，定位结果会因在454~ 491 s内、在555~582 s内、1 617~1 652 s内新增卫星有伪距偏差而相应的出现定位误差。采用删选卫星策略后，则可削弱甚至消除卫星数量跳变对定位结果的影响。

图2 可见卫星数

然后分别对GLONASS、GPS以及GLONASS/GSP双系统使用EKF、UKF进行定位解算，如图4所示。由图可知，EKF、UKF几乎全部情况下比最小二乘定位结果更接近基准值，很多情况下比接收机定位结果更准确，且当定位结果出现跳动时，EKF和UKF可有效地进行一定的平滑，使之更趋近于基准值。

为进一步分析非线性滤波融合定位算法的精度，计算了图4中各定位结果在X、Y、Z方向及3D方向的均方根误差RMSE，如表1所示。分析表1可知：对于相同的定位系统 （单系统或双系统），EKF和UKF的定位精度都比最小二乘法高，大部分方向甚至比接收机输出的定位精度要高。总体看来，UKF能得到最高的定位精度，EKF次之，ILS最低。对于相同的定位方法（ILS、EKF或UKF），双系统的定位精度基本介于两种单系统的定位精度之间。当某单一定位系统所处环境较差、定位精度较低时，通过与另一定位系统进行融合，能得到次优的结果，这牺牲了一些精度，但大大增加了定位的稳定性。

图3 删选卫星策略实验结果

图4 非线性滤波定位实验结果

3.2 恶劣环境中的定位仿真验证

3.1节验证了文中所提出的非线性定位模型和滤波算法的有效性，为进一步验证该模型的可靠性，进行恶劣环境下的定位实验。实验模拟峡谷、高楼林立等极端恶劣的情况：选择仰角最大的3颗GPS卫星和2颗GLONASS卫星，仅能观测到头顶附近卫星，且数量刚满足定位需求。此时单系统无法定位，而双系统仍可很好地应对这种恶劣情况（结果见图5）。

表1 定位误差比较

图5 恶劣情况下定位结果

与图4相比，恶劣环境下卫星数量减少，ILS算法的精度急速下降，而对于EKF和UKF，卫星数量的减少并没有对定位产生巨大影响，定位曲线平滑稳定。UKF的定位曲线相对EKF更为平滑，几乎没有卫星数量变化引起的波动。表2列出了恶劣环境实验中各方法的RMES。双系统UKF所得到的定位精度最高，EKF略低于UKF，但远高于双系统ILS的精度。

表2 恶劣环境下定位误差比较

4 结束语

文中介绍了采用伪距判别删选卫星策略的基于EKF和UKF进行双系统定位的方法。通过非线性滤波定位实验，得出文中提出的双系统融合定位算法相对于传统定位方法有更高的精度和稳定性。通过模拟恶劣环境，展示了文中提出的定位方法在单系统卫星数量不足时的绝对优势，即只需GLONASS和GPS卫星数之和不少于5颗，文中的算法仍能实现稳定可靠的高精度定位。为进一步提高双系统定位精度，文中提出的伪距判别卫星删选策略中的阈值选择可以做进一步研究，也可以深入研究其他卫星选择策略，为后续的研究打下基础。

[1]蔡昌盛，朱建军.GPS/GLONASS组合精密单点定位模型及结果分析 [J].武汉大学学报，2011，36（12）:1474-1477.

[2]罗晓敏，蔡昌盛.顾及PDOP的GPS/GLONASS组合单点定位的观测值定权[J].导航定位学报，2013，1（1）:56-60.

[3]段举举．GPS/GLONASS组合静态相位相对定位算法[J].测绘学报，2012，41（6）:825-830.

[4]Pirti A.Accuracy analysis of GPS positioning near the forest environment[J].Croatian Journal of Forest Engineering，2008（29）:189-199.

[5]Antonio A，Salvatore G，Ciro G.Performance assessment of aided Global Navigation Satellite System for land navigation [J].Iet Rader，Sonar and Navigation，2013，7（6）:671-680.

[6]成跃进.卫星导航定位系统及其导航战技术情报研究[R].五院情报报告，2013．

[7]纪龙蛰，单庆晓.GLONASS全球卫星导航系统发展概况及最新进展[J].全球定位系统，2012，37（5）：56-61．

[8]成跃进.现代卫星导航定位系统发展介绍[J].空间电子技术，2015（1）:17-25.

[9]Zhang Xiao-hong.Study on precise point positioning based on combined GPS and GLONASS[J]. Geomatics and Information Science ofWuhan University，2011，35（1）:9-12.

[10]王正军.GPS/GLONASS组合精密单点定位性能分析[J].大地测量与地球动力学，2012，32（2）:105-109.

[11]张思静.GPS/GLONASS双系统兼容定位算法研究与实现[D].北京：北京邮电大学，2011.

[12]Junping Chen.A comparative study for accuracy assessmentofPPP techniqueusingGPS and GLONASS in urban areas[J].Advances in Space Research，2015，55:125-134.

[13]Reha Metin Alkan，et al.A simplified and unified model of multi-GNSS precise point positioning[J]. Measurement，2015（69）:1-8.

[14]X Mao.NonlinearGPS ModelsforPosition Estimate Using Low-cost Receiver[C].The IEEE 6th IntelligentTransporta-tion System Conference，Shanghai，China，2003:637-642.

[15]朱萍.软件GPS接收机定位算法研究[D].上海：上海交通大学，2009.

GLONASS/GPS dual system positioning based on nonlinear filter

YAO Hui，MAO Xu-chu，WANG Jun-pu
（School of Electronic Information and Electrical Engineering，Shanghai Jiao Tong University，Shanghai 200240，China）

In order to avoid excessive dependence on one single satellite navigation system，and solve the problem that one single system cannot position in a high accuracy way under poor observation conditions，this paper proposes a method for GLONASS/GPS dual system positioning based on nonlinear filtering.This method adopts Extended Kalman filter （EKF）and unscented Kalman filter（UKF）algorithm，designs a satellite selection strategy based on analyzing pseudorange，and also apply this method to the poor environments for dual system positioning.The experiments results show that the proposed GLONASS/GPS dual system positioning method performs high accuracy and stability，especially in the poor conditions where the number of single system satellites is insufficient.

satellite navigation；GLONASS/GPS dual system positioning；Kalman filter

TN967

：A

：1674－6236（2017）01-0101-05

2015-11-30稿件编号：201511294

姚 慧（1990—），女，河北秦皇岛人，硕士研究生。研究方向：全球卫星导航系统定位。