基于Matlab自然伽马测井曲线小波降噪算法研究

2017-05-08林坤马朝选彭晓光李军科

测井技术 2017年2期

林坤, 马朝选, 彭晓光, 李军科

(中国船舶重工集团公司第七一八研究所, 河北邯郸 056027)

0 引言

在自然伽马测井中,由于核衰变的随机性质,导致自然伽马测井曲线上出现许多与地层性质无关的统计涨落和毛刺干扰,因此在对自然伽马测井曲线分析使用之前,需要对这些统计涨落和毛刺干扰进行滤波处理,只保留反映地层特性的信息[1]。本文通过几种降噪常用方法分析,使用快速傅里叶变换FFT降噪方法和小波阈值降噪方法对自然伽马测井曲线进行降噪分析,以信噪比、相关系数、降噪信号能量比和降噪信号与原信号均方差4个性能指标,对降噪效果进行对比,得到最佳的降噪方案。

1 小波变换算法的理论分析

小波变换在许多工程领域都得到了广泛的应用[2]。对于任意ψ(t)∈L2(R),即ψ(t)是平方可积函数,如果ψ(t)的傅里叶变换满足可容许条件

(1)

式中,R*=R-{0}表示非零实数全体,则称ψ(t)是小波母函数。对于任意的实数对(a,b),其中参数a必须为非零实数,称式(2)形式的函数为小波基函数

(2)

对于任意能量有限信号f(t)其小波变换定义为

(3)

1.1 一维离散小波分解和重构算法

一维离散小波变换给定一个长度为N的信号s,第1步从原始信号s开始,产生2组数据,一组是作用于低通滤波器Lo_D得到的近似系数cA1;另一组是作用于高通滤波器Hi_D得到的细节系数cD1。这2个系数都是原信号在滤波器作用下以尺度为2的下采样。一维小波分解算法见图1。

图1 一维小波分解算法

第2步采用同样做法,把其中的低频部分作为信号再次分解,以3层小波分解为例,图形表示见图2。

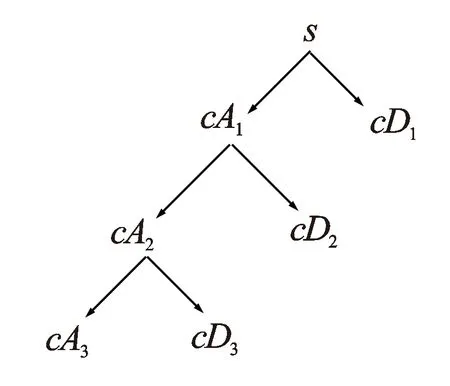
图2 3层小波分解示意图

首先对信号s进行3层小波分解,cA为近似系数,cD为细节系数。噪声信号通过包含在细节系数cD中,通过门限阈值对细节系数进行处理;对信号进行重构可以达到降噪的目的。对信号s(t)降噪的目的就是抑制信号的噪声,从而在s(t)中恢复真实信号f(t)。

重构算法是小波变分解算法的逆变换,把分解得到的近似系数和细节系数通过低通滤波器和高通滤波器重构得到原信号。

2 小波降噪算法判定准则和模型

2.1 小波降噪算法判定准则

测井信号的降噪效果可以通过信噪比、相关系数、能量比和均方差来衡量和评价[3-5]。

(1) 信噪比。信号信噪比RSN定义为

(4)

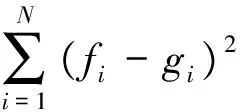
(2) 相关系数。用于计算小波函数与原测井信号波形的相似程度,相似程度越高,则对原数据信号进行逼近的时候产生的加权求和项就越小。ρxy为小波函数x与信号y的相似系数

(5)

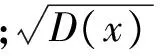
(3) 能量比。降噪后的测井信号与原测井信号大部分情况下要有相同的光滑性,降噪后的测井信号与原测井信号的能量比越大,光滑性越好。

(4) 均方差。降噪后的测井信号和原测井信号的方差估计应该是最坏情况下的方差最小,任意算法的降噪偏差均方差EMS为

(6)

2.2 小波降噪的基本模型

在实际工程应用中,通过所分析的信号具有非线性、非平稳性和奇异点较多的特点[6]。含噪声的一维信号模型可表示为

s(t)=f(t)+σ·e(t)

(7)

式中,s(t)为含噪声的信号;f(t)为有用信号;e(t)为噪声;σ为噪声强度。

小波变换降噪方法与步骤见文献[7]。

3 小波基函数选取

小波基函数选取一般原则[8-10]。①正交性,便于数学分析和工程应用中理解操作;②紧支集,保证有优良的时域局部特征,也利于算法的实现;③对称性,关系到小波的滤波特性是否具有线性相位,这与失真问题密切相关;④平滑性,关系到频率分辨率的高低。

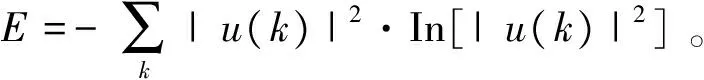
4 自然伽马测井曲线降噪

4.1 信号降噪常用方法分析

4.1.1 通过快速傅里叶变换FFT实现信号降噪

首先对原信号进行快速傅里叶变化FFT,求出原信号的频谱;根据得到的信号频谱,对所需要的频谱成分保留,对不需要的信号频谱成分进行抑制;对FFT变换后的频谱做傅里叶逆变换,得到降噪后的信号。这个过程是对原信号在一定范围滤波,还原到时域则相当于对信号进行卷积运算。设原信号为f(t),降噪后的信号为g(t),其傅里叶变换形式为F(ω)和G(ω)。则G(ω)=H(ω)F(ω),其中H(ω)为频域的滤波器,用于抑制噪声信号的频谱。

4.1.2 小波阈值实现信号降噪

小波阈值降噪方法通过对小波分解后的各层系数中模大于阈值和小于某阈值的系数分别处理;对处理完的小波系数再进行小波重构变换,重构出降噪后的信号[11-12]。

(1) 使用penalty软阈值实现信号阈值降噪。使用函数wnoisest获取噪声方差;使用函数wbmpen获取小波去噪阈值;使用函数wdencmp实现信号去噪。

sigma=wnoisest(c,l,1)

thr3=wbmpen(c,l,sigma,2)

xd3=wdencmp(′gbl′,c,l,wname,lev,thr3,′s′,1);

(2) 使用Birge-Massart分层硬阈值实现信号阈值降噪。使用函数wdcbm获取小波去噪阈值;使用函数wdencmp实现信号去噪。

[thr4,nkeep]=wdcbm(c,l,3,)

[xd4,cxd,lxd,perf0,perfl2]=wdencmp(′lvd′,c,l,wname,lev,thr4,′h′);

(3) 使用全局软阈值实现信号阈值降噪。在Matlab中使用函数ddencmp获取信号去噪阈值;采用函数wdencmp实现信号去噪。

[thr5,sorh,keepapp]=ddencmp(′den′,′wv′,x)

xd5=wdencmp(′gbl′,x,′db4′,4,thr5,′s′,keepapp);

4.1.3 基于样本估计的自适应阈值实现信号降噪

对信号做无偏似然估计,根据最坏情况下降噪信号与原信号方差最小的原则确定一个统一的阈值,然后截去超出这个阈值的系数。

(1) 使用rigrsure自适应软阈值降噪

thr6=thselect(x,′rigrsure′)

xd6=wdencmp(′gbl′,c,l,′db4′,4,thr6,′s′,1);

(2) 使用sqtwolog自适应软阈值降噪

thr7=thselect(x,′sqtwolog′)

xd7=wdencmp(′gbl′,c,l,′db4′,4,thr7,′s′,1);

(3) 使用heursure自适应软阈值降噪

thr8=thselect(x,′heursure′)

xd8=wdencmp(′gbl′,c,l,′db4′,4,thr8,′s′,1);

(4) 使用minimaxi自适应软阈值降噪

thr9=thselect(x,′minimaxi′)

xd9=wdencmp(′gbl′,c,l,′db4′,4,thr9,′s′,1);

4.2 自然伽马测井曲线降噪效果分析

分别使用快速傅里叶变换降噪算法1、penalty软阈值降噪算法2、Birge-Massart分层硬阈值降噪算法3、全局软阈值降噪算法4、rigrsure自适应软阈值降噪算法5、sqtwolog自适应软阈值降噪算法6、heursure自适应软阈值降噪算法7和minimaxi自适应软阈值降噪算法8对自然伽马测井曲线进行了降噪,降噪后的信噪比、相关性、能量比和均方差指标对比见图3。

图3 降噪算法指标对比

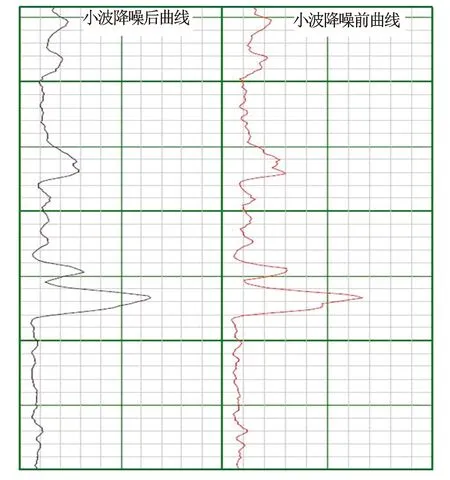
图4 自然伽马测井曲线滤波前后曲线

从图3可见,在使用小波阈值降噪方法2～8进行噪声抑制的时候,降噪后的信噪比、相关系数和能量比都比通过傅里叶变换降噪方法1的大,降噪后的均方差比通过傅里叶变换降噪方法1的小,说明通过小波阈值降噪方法2～8降噪效果好,降噪后的信号与原信号保持了很好的相似性,光滑性好。在小波阈值降噪方法2～8的7种降噪方法中,降噪方法5和7信噪比高,均方差小,说明降噪方法5和7的降噪结果最优。

自然伽马测井曲线使用rigrsure自适应软阈值小波降噪算法前后的曲线见图4。从图4可见,经过该方法降噪后的测井曲线比较光滑,无尖棱毛刺。该方法在对自然伽马测井曲线降噪中有较好的滤波效果,能有效去除自然伽马测井曲线中与地层信息无关的统计涨落和毛刺干扰。