Joint Optimal Energy-Efficient Cooperative Spectrum Sensing and Transmission in Cognitive Radio

Weizhi Zhong, Kunqi Chen, Xin Liu ,

1 College of Astronautics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;

2 School of Information and Communication Engineering, Dalian University of Technology, Dalian 116024, China

I.INTRODUCTION

CR has been proposed to solve the spectrumscarcity problem, owing to its opportunistic transmission and dynamic spectrum access capabilities [1].In CR, SU can utilize the licensed spectrum dynamically when the spectrum is temporally unused [2-4].To avoid interference to the normal communication of primary user (PU), SU needs to use spectrum sensing to detect whether PUs are present or not before its secondary transmissions [5].If the presence of the PU is detected, SU should postpone its transmissions.However, reliable spectrum sensing cannot always been guaranteed due to multipath fading, shadowing and hidden terminal problem.CSS has thus been proposed to improve the sensing accuracy.In CSS, several SUs sense the spectrum independently and then deliver their sensing data to a fusion center that makes the final judgment of the PU status [6].

Most of previous works in the literature are focused on optimizing either cooperative sensing or transmission parameters to maximize the throughput of the whole CR system [7,8].The optimal sensing- throughput tradeoff is investigated in [9] for the single-channel CR,and the multi-channel CR is also discussed in[10].Both of [9] and [10] assume each SU to have a fixed transmission power and ignore the considerable potential gain of dynamic resource allocation.Therefore, the joint optimization of spectrum sensing and resource al-location is investigated in [11] and [12] for the cases of single user and multiple users respectively, which considers the dynamic allocation and increases the throughput of the CR system observably.

In this paper, a joint optimal energy-efficient cooperative spectrum sensing(CSS) and transmission in multi-channel CR is proposed to improve the energy efficiency(EE) in cognitive radio(CR).

All the researches above pay attention to the throughput of CR.Nevertheless, due to the popularity and significance of green communication, EE has spurred great interest in recent years.Since most of the mobile terminals in wireless networks are battery-powered, EE is critical to the service life of these terminals[8,13].In the literature, energy-efficient cooperative sensing for CR networks is investigated in [14,15].The authors aim at maximizing the energy-efficient capacity via optimizing either the sensing time or detection threshold.The optimal energy-efficient power allocation is studied in [7], which assumes the sensing factors fixed.Furthermore, the joint optimization of energy-efficient sensing and transmission in the single-channel CR is considered in[16,17].However, to reduce the complexity and non-convexity of the initial optimization issues, most of the energy-efficient optimizations ignore the miss detection, where SUs fail to detect the presence of PU and access the spectrum, thus yielding awful energy waste and deviation from the real communication Moreover, the joint optimization of energy-efficient CSS and transmission in multi-channel CR has not been considered in current researches.

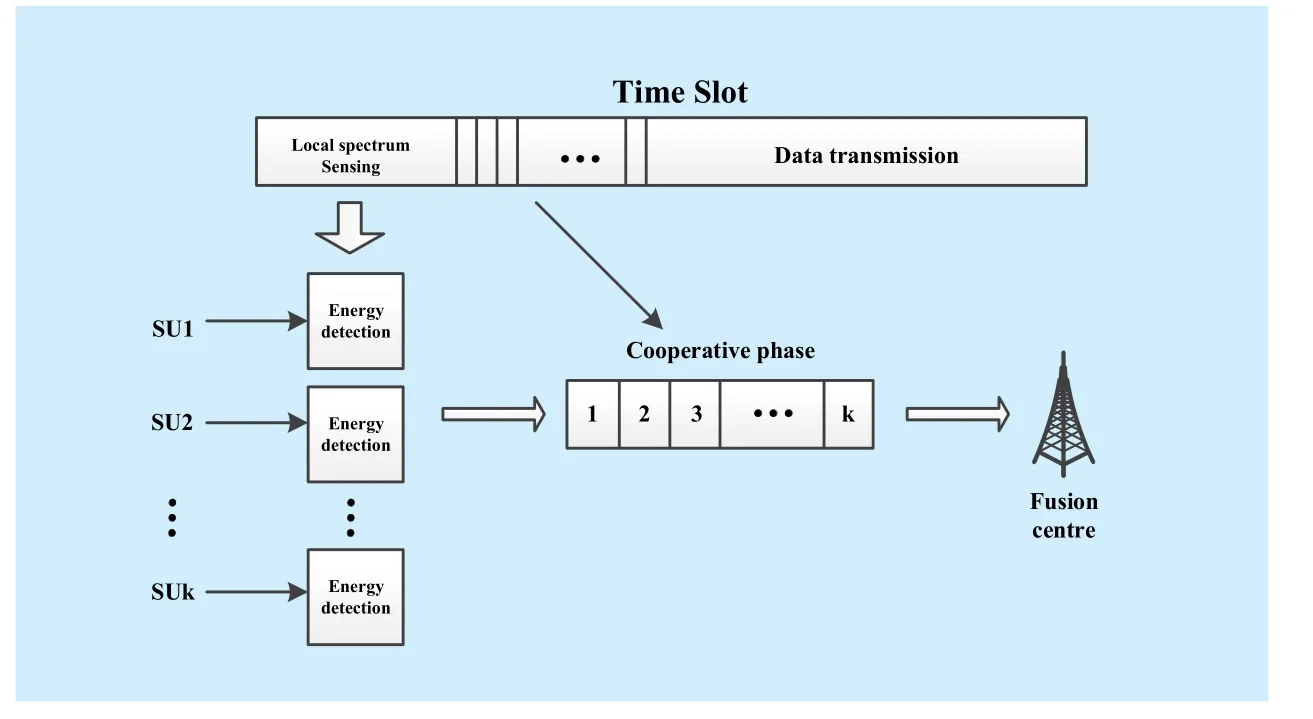
Fig.1 Cooperative spectrum sensing model

Hence, in this paper, we investigate the joint optimization of cooperative spectrum sensing,including sensing time and the number of cooperative users, and data transmission, including proportion of bandwidth and transmission power, for multi-channel CR.Besides, we also consider miss detection to formulate a holistic and significant energy-efficient optimization scheme.

The rest of this paper is organized as follows.The system model is introduced and an energy-efficient optimization problem is formulated in Section Ⅱ .Then, in Section Ⅲ , a combined algorithm of bi-level optimization,Polyblock optimization and Dinkelbach’s optimization is proposed to solve the proposed non-convex optimization problem.Simulation results and conclusions are finally presented in Section Ⅳ and V, respectively.

II.SYSTEM MODEL

In this paper, the cognitive radio network(CRN) consists ofLlicensed channels andNsecondary users.The bandwidth of each licensed channel isB.

We assume the system is strictly synchronized and a time-slot scheme is considered which divides the communication time into several slots with lengthT.In order to simplify the problem, each PU is also assumed to keep their status unchanged in each time slot.Moreover, each slot contains three phases[12], including local sensing phase, cooperative phase and transmission phase.The timeslot structure is shown in Fig.1.

First, some SUs are chosen to perform the cooperative sensing.During the local sensing phase, they sense the PU status independently with a sampling rateThen, in the cooperative phase, these SUs deliver their own sensing statistics to a fusion center that makes the final judgment of the PU status [18].To save the bandwidth of the common channel and prevent the conflict of cooperative information of the SUs, the delivery can be implemented via time division multiple access (TDMA).Finally, in the transmission phase, all SUs access the usable channels to transmit their data according to the judgment of the fusion center.

2.1 Cooperative spectrum sensing

During the local spectrum sensing phase, each SU senses the signal by spanning the objective channels.The signal received by their receivers follows a binary hypothesis as follows [9]:

Energy detection is the most widely used spectrum sensing method because it can be easily implemented without knowing any prior knowledge from the PU.Energy detection is conducted by comparing the metrical energy statistic of the received PU signal with a pre-configured decision threshold.If the energy is higher than the threshold, the PU is assumed to be busy; otherwise, the PU would be judged as idle [19-22].

Using energy detection, the energy statistic of each SU can be given as

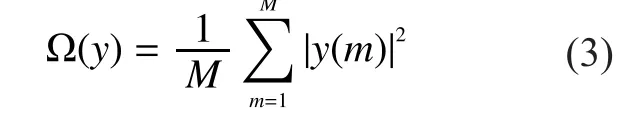
According to CSS, the fusion center collects energy statistics from all SUs and makes the final judgment of the PU status.IfkSUs are chosen to sense PU cooperatively, the global energy statistics collected by the fusion center can be given as

Furthermore, if the pre-configured decision threshold isthe false alarm and detection probabilities of CSS can be given, respectively, by following [9,11] as

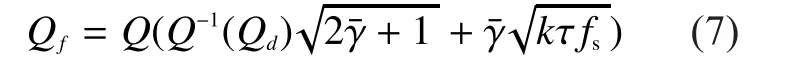
2.2 Throughput of SU

In the transmission phase, each SU is assigned a portion of each usable channel at a certain transmission power [12].In this paper,we assume theith SU is assigned a portionof thejth channel, which can be realized via either the Filter Bank Multicarrier (FBMC) or orthogonal frequency division multiple access (OFDMA), at a transmission power.Moreover, the channel gains from the PU transmitter to the SU receiver and from the SU transmitter to its own receiver are respectively denoted byand.

a) Channeljis indeed idle and no false alarm appears.The probability of this scenario iswhereis the idle probability of channelj.In this case, the SU’s achievable transmission rate is

In CR system, SU can access one channel only when the PU status in this channel is judged as idle.Actually, SU may access the channel in the following two scenarios [9,12].

b) Channel j is actually busy but it is not accurately detected.The probability of this scenario iswhereis the busy probability of channelj.In this case, the PU’s signal serves as interference to SU’s communication; hence the SU’s achievable transmission rate is

In addition, we suppose that the length of the time slot used by each cooperative SU to deliver local sensing data to the fusion center isξ.When using TDMA, the cooperative overhead is given as

Then the transmission duration is given as

Therefore, the throughput of all SUs is given as

2.3 Traditional optimization model

For the sake of explanation and contrast, we first propose a joint global optimization of CSS and transmission in multi-channel CR to maximize the throughput.

To ensure the accuracy of spectrum sensing, a lower limit of cooperative detection probability should be set beforehand and the traditional throughput maximization problem is formulated in [9] as

Problem P0:

However, Problem P0 does not consider CSS and the transmission optimization.Generally speaking, in CSS, the false alarm and detection probabilities mainly depend on the local sensing duration and the number of cooperative SUsk.In fact, the increase ofandkleads to a higher detection probability and a lower false alarm probability, which implies a better sensing capability, but also means less time and power for the later data transmission.Thus, there is a tradeoff between CSS and throughput.

Hence, we first upgrade the tradition optimization model by further considering CSS and transmission optimization as follows

Problem P1:

Although Problem P1 is a new optimization model, its objective function is just a part of Problem P2 introduced in detail later.Therefore, Problem P1 can be solved by a combination of bi-level optimization and Polyblock optimization.Moreover, a similar basic model is proposed in [12] and the optimization procedure in [12] can be taken as reference to solve Problem P1.

Hereinafter, we formulate our EE maximization model and make a comparison between the two models to demonstrate our scheme by some simulations.

2.4 Energy efficiency maximization model

When concerning energy efficiency, a good choice for the objective function of the optimization problem is one that measures the number of bits that can be transmitted per joule of energy consumed [13].In a communication system, a high power is often required to reach a high signal-noise-rate (SNR) level,which can lead to a lower bit-error-rate (BER)and thus a higher throughput.However, a high power means low battery life for the terminals and is also not eco-friendly.Thus the objective function of EE can be defined as a tradeoff between the throughput and the entire power consumed in a time slot, including both the sensing and transmission power.Furthermore,this tradeoff can be formulated as follows

The objective function in (14) was introduced in [23] and has been adopted as the definition of EE in many researches [8, 24-25].

According to (14), we formulate the objective function of EE in CSS as (15) shown in the bottom at this page.

Based on the above analysis, the EE maximization problem can be formulated as Problem P2 shown in the bottom at this page.

II.JOINT EE OPTIMIZATION OF COOPERATIVE SPECTRUM SENSING AND TRANSMISSION

Problem P2 is actually a mixed-integer non-convex problem, which is usually NP-hard to solve directly.To solve Problem P2,we first transform the problem into a low complexity form.

Becausekis within a finite integer set, we can optimizekby exhaustive searching.Next,we mainly investigate the optimization of

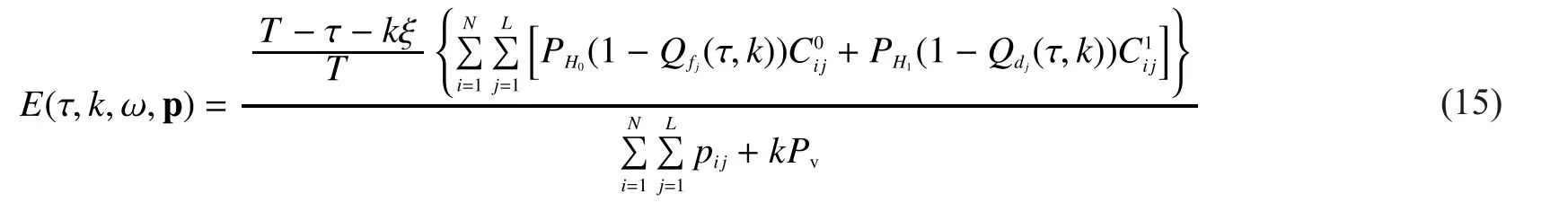
Problem P2:with a specifickvalue as Problem P4 (with a specifickvalue) shown in the bottom at this page.

However, Problem P4 is still not convex.To solve this problem, we adopt the bi-level optimization to divide Problem P4 into two sub-level optimization problems.The lower one is to optimizeandwith specifickandwhile the upper one is to optimize.The lower level problem is given as Problem P5(with specifickandvalue) shown in the bottom at this page.

which is equivalent to Problem P6 (with specifickandvalue) shown in the bottom at this page.

Problem P3:

Problem P4 （with a specifickvalue）:

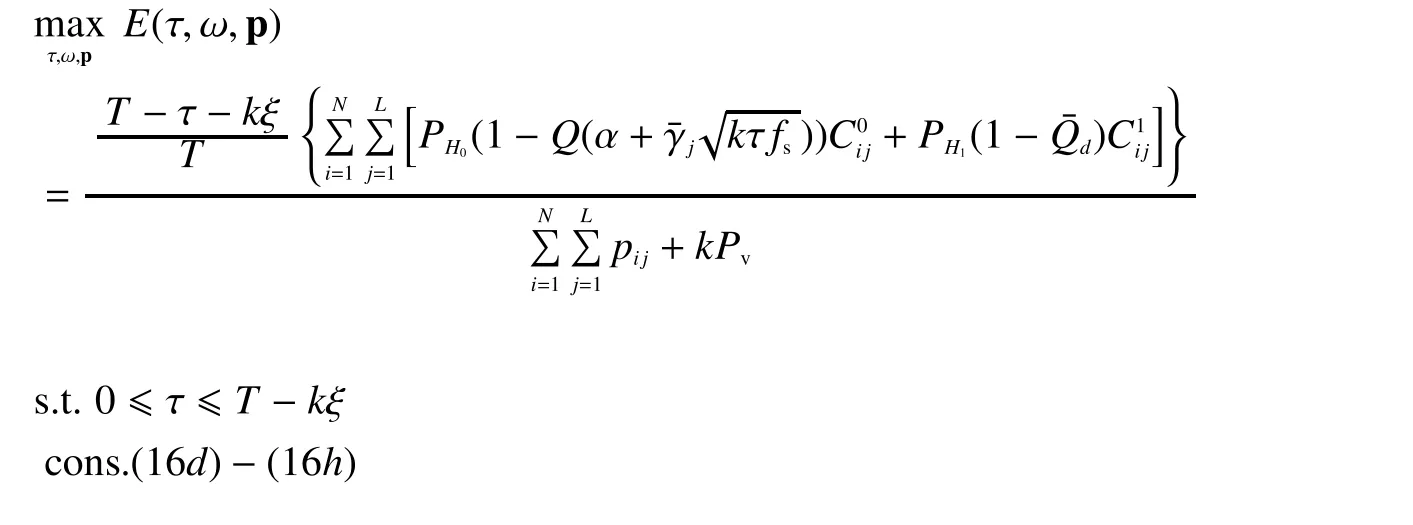
Problem P5 （with specifickandvalue）:

Problem P6 （with specifickandvalue）:

Problem P7:

The Problem P6 is a fractional optimization problem.The numerator and denominator of its objective function can be denoted asandrespectively, i.e.(17)shown in the bottom at this page.

Notice that the feasible region of Problem P6 is a convex, compact and connected set.Bothandare continuous and positive-valued functions in the feasible region of Problem P6.Meanwhile,is a concave function from [26], andis a linear function.Therefore, based on [27] and[28], Problem P6 can be solved by Dinkelbach’s optimization, where the fractional problem is represented by an equivalent parametric program that is convex for a concave-linear fractional program and can be rapidly solved by an iterative procedure.

The feasible region of Problem P6 is denoted as.Then, the procedure of Dinkelbach’s optimization for Problem P6 is described as Algorithm 1.

Thus, the optimal solution offor specifickandcan be obtained.For Problem P7, we have the following lemma.

Lemma 1: Functionsandare monotonically increasing functions with respect towithin the interval

Proof: SupposewhereWhenandthe optimal solutions ofareandrespectively.Since the functionis a monotonically increasing function with respect towithin the intervalwe have

According to lemma 1, the objective function of Problem P7 is the difference of two monotonically increasing functions whose intervals are both non-negative.Thus, by introducing a variable, Problem P7 can be transformed into a monotonic optimization problem, which can be solved through Polyblock optimization [29].

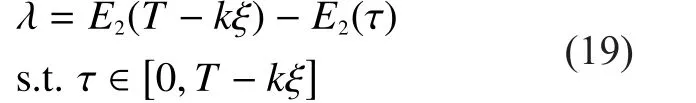
Problem P8:

Algorithm 1 Dinkelbach’s optimization for Problem P6 (with specific k and τ value)

Algorithm 2 Polyblock optimization for Problem P9 (with a specific k value)

Algorithm 3 k -Exhaustion Algorithm for Problem P3

Table I The SCSNR of each SU on each licensed channel

Problem P9:

Problem P9 is a monotonic optimization problem because its objective function and constraints are all monotonically increasing functions.Since bothτandare non-negative, Problem P9 can be solved by Polyblock optimization [30,31] as shown in Algorithm 2.

Thus, with a specifick,the outputxof Algorithm 2 is the optimal solution of the upper Problem P9 andBased on the above analysis, we can now use the exhaustive algorithm to searchkand formulate a general algorithm to solve Problem P3 as shown in Algorithm 3.

IV.SIMULATION RESULTS

In this section, simulation results are presented by comparing the energy efficiency maximization model (EEMM) with the traditional throughput maximization model (TMM) to demonstrate our scheme.

Consider a CR network consisting ofN=6 SUs andL=8 licensed channels.Each channel spans a bandwidthThe sampling frequency isthe length of time slot isthe time used by each cooperative SU to deliver local sensing data to the fusion center isthe transmission power of PU signal isthe sensing power of each cooperative SU isthe maximal transmission power of each SU isand the lower limit of detection probability isBoth the idle and busy probabilities of these channels are

In the simulations, with different pairs of specifickandτ, we can obtain the optimal utilities of Problem P2 (i.e.EEMM) and Problem P1 (i.e.TMM) by Algorithm 1 and the interior-point method, respectively.

First, we demonstrate the effect, caused by the local sensing durationτand the number of chosen cooperative sensing SUsk,on EE and throughput in both the two models (EEMM and TMM).Fig.2 shows the EE of the whole CR systemversusτwith differentkwhenandFig.3 shows the throughput of the whole CR systemversusτwith differentkwhenandIt can be seen that, with the increase ofτ, all the optimal utilities first increase and then decrease.In fact, the increase ofτleads to a lower false alarm probability,which implies a better sensing capability and thus a higher EE and throughput of the CR system.Thus the optimal utilities increase at first.However, with the increase ofτ, the effect is wearing off.Whenτreaches a certain value, the loss of transmission time, caused by the increase ofτ, becomes dominant.Hence,the optimal utilities decrease later.Besides, the increase ofkalso has a similar effect on the optimal utilities.We also indicate the optimal, achieved by Algorithm 2 with differentkindependently, and the corresponding utilities in Fig.2.It can be seen that each of the marked utilities is very close to their correspondingk-fixed global optimal utilities, which perfect-ly verifies the effectiveness of our proposed algorithm.In addition, by comparing the utilities of differentwe find out the global optimal solution through Algorithm 3.Whenk=4 andτ=0.0743s, the CR system based on EEMM can achieve the global optimal utility.Moreover, although the obtainedof EEMM is less than that of TMM, the obtainedof EEMM is much more than that of TMM.This result verifies the principles of both EEMM and TMM perfectly.

Table II The TCSNR of each SU on each licensed channel

Fig.2versus with different k when

Fig.3versus with different k when

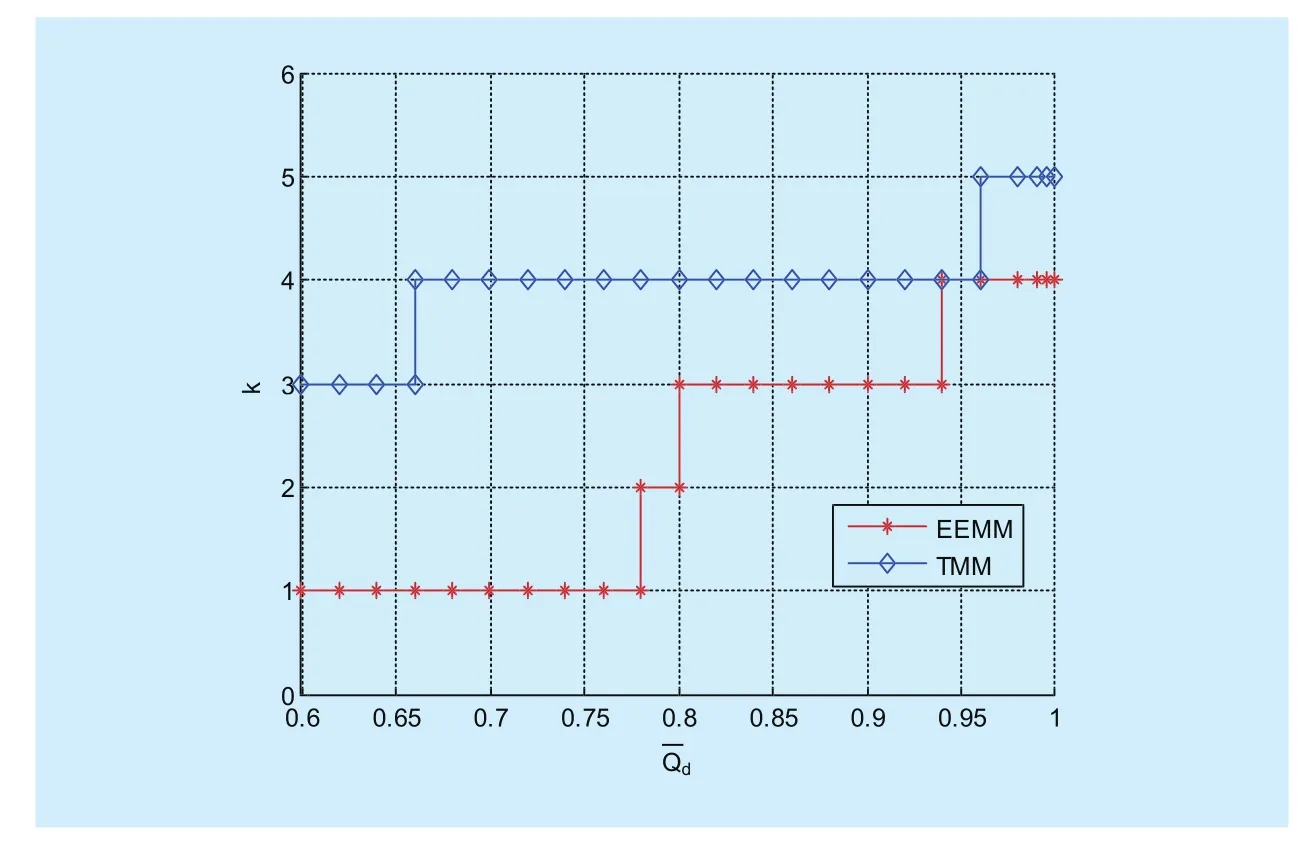
Fig.6 k versuswith different models

Then, we focus on the effect of the lower limit of cooperative detection probabilityin our scheme.In the following simulations, the optimal solutions of EEMM and TMM are respectively given by Algorithm 3 and a similar Polyblock optimization proposed in [12].For the sake of demonstration, we use power utilization ratiowhich represents the power consumption required to accomplish the desired communication preference when the maximum power limit is given, to describe the usage of power in CR system.Furthermore,can be formulated as the ratio of the total consumed power to the total maximal transmission power of all SUs, i.e.

Finally, we demonstrate the effect of the maximal transmission power of each SUin our scheme.Fig.7, Fig.8 and Fig.9 showsversuswith different models,respectively.From Fig.7, it can be seen that, asgrows,of TMM first increases and then decreases.The prime increase is due to the increase of the throughput.However, sinceof TMM is always 100%, whenreaches a certain value, the excessive consumption of power becomes dominant, which finally leads to the decrease of EE.In contrast, EEMM can limit the power consumption effectively.In Fig.7,with the increase ofof EEMM also increases at first, which is due to the increase of the throughput.However, whenrises toreaches an upper bound and almost keeps invariable later, which indicates the increase ofgradually becomes a waste of resources and the limit on power consumption in EEMM is effective.Moreover, like Fig.4, the obtainedof EEMM is always higher than that of TMM, even in the common ascent stage.In Fig.8, the initial stage of EEMMshows dramatic fluctuations.According to Fig.9, the fluctuations are mainly caused by the interaction of the increase ofkandEven whenrises to 0.0060W, wherekincreases from 3 to 4, the trend of the curve also experiences a slight change.Moreover, oncekis fixed, the useless increase ofgradually becomes more and more severe and directly leads to the periodic decreases of.

V.CONCLUSION

Fig.7versus with different models

Fig.8versus with different models

Fig.9 k versus with different models

In this paper, a joint optimal energy-efficient CSS and transmission in multi-channel CR system is investigated.A joint optimization problem is formulated to maximize EE by jointly optimizing local sensing time, number of cooperative sensing SUs, transmission bandwidth and power.This non-convex problem is effectively solved by a combination of bi-level optimization, Polyblock optimization and Dinkelbach’s optimization.Finally, we demonstrate the effectiveness of EEMM by comparing it with TMM.Simulation results show that EEMM has a significant improvement on the EE performance and performs a valid limit to the power consumption.

ACKNOWLEDGEMENTS

This work was supported by the National Natural Science Foundations of China under Grant Nos.61301105, 61401288 and 61601221;the Natural Science Foundations of Jiangsu Province under Grant No.BK20140828; the China Postdoctoral Science Foundations under Grant Nos.2015M581791 and 2015M580425;and the Fundamental Research Funds for the Central Universities under Grant No.DUT16RC(3)045.

[1] T.Cui, F.Gao, A.Nallanathan.“Optimization of Cooperative Spectrum Sensing in Cognitive Radio”.IEEE Transactions on Vehicular Technology,vol.60, no.4, pp 1578- 1589, 2011.

[2] W.Krenik, A.Batra.“Cognitive radio techniques for wide area networks”.Design Automation Conference, 2005.Proceedings.vol.30, no.5, pp 409-412, 2005.

[3] S.Huang, X.Liu, Z.Ding.“Optimal Transmission Strategies for Dynamic Spectrum Access in Cognitive Radio Networks”.IEEE Transactions on Mobile Computing, vol.8, no.12, pp 1636-1648,2009.

[4] S.Bayhan, F.Alagoz.“Scheduling in Centralized Cognitive Radio Networks for Energy Efficiency”.IEEE Transactions on Vehicular Technology,vol.62, no.2, pp 582-595, 2013.

[5] H.Jiang, L.Lai, R.Fan, et al.“Optimal selection of channel sensing order in cognitive radio”.IEEE Transactions on Wireless Communications,vol.8, no.1, pp 297-307, 2009.

[6] J.Marinho, E.Monteiro.“Cooperative Sensing-Before -Transmit in Ad-Hoc Multi-hop Cognitive Radio Scenarios”.Lecture Notes inComputer Science, pp 186-197, 2012.

[7] Y.Wang, W.Xu, K.Yang, et al.“Optimal Energy-Efficient Power Allocation for OFDM-Based Cognitive Radio Networks”.IEEE Communications Letters, vol.16, no.9, pp 1420-1423, 2012.

[8] M.Haddad, Y.Hayel, O.Habachi.“Spectrum Coordination in Energy-Efficient Cognitive Radio Networks”.IEEE Transactions on Vehicular Technology, vol.64, no.5, pp 2112-2122, 2015.

[9] Y.C Liang, Y.Zeng, E.C.Y Peh.“Sensing-throughput tradeoff for cognitive radio networks”.IEEE Transactions on Wireless Communications, vol.7, no.4, pp 1326-1336, 2008.

[10] R.Fan, H.Jiang.“Optimal multi-channel cooperative sensing in cognitive radio networks”.IEEE Transactions on Wireless Communications,vol.9, no.3, pp 1128-1138, 2010.

[11] X.Liu, G.Bi, Y.L Guan, et al.“Joint optimization algorithm of cooperative spectrum sensing with cooperative overhead and sub-band transmission power for wideband cognitive radio network”.Transactions on Emerging Telecommunications Technologies, vol.26, no.4, pp 586-597,2015.

[12] R.Fan, H.Jiang, Q.Guo, et al.“Joint Optimal Cooperative Sensing and Resource Allocation in Multichannel Cognitive Radio Networks”.IEEE Transactions on Vehicular Technology, vol.60,no.2, pp 722 - 729, 2011.

[13] F.Meshkati, H.V Poor, S.C Schwartz.“Energy-Efficient Resource Allocation in Wireless Networks”.IEEE Signal Processing Magazine, vol.24,no.3, pp 58-68, 2007.

[14] O.Ergul, O.B Akan.“Energy-efficient Cooperative Spectrum Sensing for Cognitive Radio Sensor Networks”.IEEE Symposium of Computers and Communications (ISCC), pp 465-469, 2013.

[15] E.C.Y Peh, Y.C Liang, Y.L Guan, et al.“Energy-Efficient Cooperative Spectrum Sensing in Cognitive Radio Networks”.Global Telecommunications Conference (GLOBECOM 2011), IEEE, pp 1-5, 2011.

[16] Y.Gao, W.Xu, K.Yang, et al.“Energy-efficient transmission with cooperative spectrum sensing in cognitive radio networks”.Wireless Communications and Networking Conference (WCNC),IEEE, pp 7-12, 2013.

[17] X.Wu, J.L Xu, M.Chen, et al.“Optimal Energy-Efficient Sensing and Power Allocation in Cognitive Radio Networks”.Mathematical Problems in Engineering, no.3, pp 1-7, 2014.

[18] X.Liu.“A new sensing-throughput tradeoff scheme in cooperative multiband cognitive radio network”.Inter- national Journal of Network Management, vol.24, no.3, pp 200-217, 2014.

[19] Z.P Liang, R.Z Song, Q.Z Lin, et al.“A double-module immune algorithm for multi-objective optimization problems”,Applied Soft Computing,vol.35, no.C, pp 161-174, 2015.

[20] Q.Z Lin, J.Y Chen, “A novel micro-population immune multiobjective optimization algorithm”,Computers & Operations Research, vol.40, no.6,pp.1590-1601, 2013.

[21] J.Y Chen, Q.Z Lin, Q.B Hu, “Application of novel clonal algorithm in multiobjective optimization”,International Journal of Information Technology& Decision Making, vol.9, no.2, pp.239-266,2010.

[22] J.Y Chen, Q.Z Lin, L.L Shen, “An immune-inspired evolutionary strategy for constrained optimization problems”, International Journal on Artificial Intelligence Tools, vol.20, no.3, pp.549-561,2011.

[23] V.Shah, N.B Mandayam, D.J Goodman.“Power control for wireless data based on utility and pricing”.IEEE International Symposium on Personal, Indoor and Mobile Radio Communications,vol.3, pp 1427-1432, 1998.

[24] C.U Saraydar, N.B Mandayam, D.Goodman.“Pricing and Power Control in a Multicell Wireless Data Network”.IEEE Journal on Selected Areas in Communications, vol.19, no.10, pp 1883-1892, 2001.

[25] F.Meshkati, H.V Poor, S.C Schwartz, et al.“An energy-efficient approach to power control and receiver design in wireless data networks”.IEEE Transactions on Communications, vol.53, no.11, pp 1885-1894, 2005.

[26] X.Gong, S.A Vorobyov, C.Tellambura.“Joint Bandwidth and Power Allocation With Admission Control in Wireless Multi-User Networks With and Without Relaying”.IEEE Transactions on Signal Processing, vol.59, no.4, pp 1801-1813, 2011.

[27] W.Dinkelbach.“On Nonlinear Fractional Programming”.Management Science, vol.13, no.7,Series A, Sciences, pp 492-498, 1967.

[28] S.Schaible.“Fractional Programming.II, On Dinkelbach’s Algorithm”.Management Science,vol.22, no.8, pp 868-873, 1976.

[29] S.Alizamir.“Monotonic Optimization”.Encyclopedia of Optimization, pp 2316-2323, 2009.

[30] S.Boyd, L.Vandenberghe.“Convex Optimization”.Cambridge University Press, 2004.

[31] C.Floudas, P.M.Pardalos.“Encyclopedia of Optimization”.Springer-Verlag GmbH, 2008.