A Block Parallel l0-Norm Penalized Shrinkage and Widely Linear Affine Projection Algorithm for Adaptive Filter

Youwen Zhang, Shuang Xiao＊, Lu Liu, Dajun Sun

1 Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China

2 College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China

* The corresponding author, email: xiaoshuang@hrbeu.edu.cn

I.INTRODUCTION

One major drawback of the least mean square(LMS) algorithm is its slow convergence rate for colored input signals and the affine projection (AP) algorithm is a better alternative to LMS in such an environment [1].It is regarded as the generalization of the normalized LMS(NLMS) algorithm which exploits the(e.g.the projection order) most recent input signal to update the tap-weight vector thus its convergence rate is enhanced [2].In some occasions,it may achieve a performance that rivals with the recursive least squares (RLS) algorithm at a lower computational cost.As a result, AP algorithm is widely used in many adaptive applications such as system identification, active noise control (ANC) [3] and acoustic echo cancellation (AEC) [4] and so on.

However, the application of conventional AP algorithm is limited in some occasions because it uses a fixed step-size parameter.This may lead to poor performance especially for fast change system and the non-stationary incoming signals.Aiming at this problem,many modified algorithms come out, such as the algorithms in [5]-[7].The proportionate AP algorithm (PAPA) and the improved PAPA(IPAPA) are proposed in [5] obtain the stepsize proportionated with the corresponding tap.In [6] the variable step-size AP algorithm(VSSAPA) exploits the estimate error power to calculate the step-size.The shrinkage linear AP (SHAP) algorithm is proposed in [7] adjusts the step-size by minimizing the Euclidean norm of the noise-freea posteriorianda priorierrors.All these provide a variable step is close to the optimal one at each iteration and the convergence rate and tracking ability are improved.

In this paper, the authors proposed a block parallel l0-SWLDCD-AP algorithm for the time-varying sparse communication system.

Although the variable step-size can track the system more efficiently, they have not consider the specific conditions such as the sparsity system, which is a common phenomenon in wireless communications, medical imaging and so on.The typical feature of a sparse system is its impulse response contains few non-zero values [8].An efficiently method to solve this problem is to utilize the sparsity-promoting constraint [8]-[13].The constraint suggests a zero-attractor in the update function which can enhance the performance of the zero value tap.Based on this idea, the zero-attracting AP algorithm (ZA-APA) and the reweighted ZA-APA (RZA-APA) [12], the affine projection algorithm for sparse system identification (APA-SSI) and quasi APA-SSI(QAPA-SSI) [13] are proposed.These algorithms can demonstrate better performance than the AP algorithm in many sparse scenarios, even at low sparsity level.

In the conventional adaptive signal processing field, these signals are considered as proper or circular, which mean the signals are uncorrelated with their conjugate forms and their probability distribution is invariant when rotate in the complex plane [14].However, the widely used signals, such as BPSK,PAM, GMSK, off-set QPSK and so on, are the noncircular signals according to recently research [15].The circular assumption ignores second-order properties of the signals [16], so the algorithms which are optimal for circular signals may lead to suboptimal performance for noncircular signals [17].The widely linear processing applied in [14]-[20] makes efforts to solve this problem.It suggests the combination of incoming signal and its conjugate form as the input of the adaptive filter, so the second-order properties of the signal are fully used.The method has already applied in the LMS algorithm [19], [20] and result shows that the performance is improved.

The computational complexity of AP algorithm is one of the tricky obstacle that restricts its application, especially for largeTo solve the problem, many fast affine projection (FAP)algorithms have been proposed [21]-[24].All of them lead to simpler performance only when the step-size is close to 1, so the benefit is limited obviously.In [25], the author proposed a dichotomous coordinate descent AP (DCDAP) algorithm which can reduce computational complexity without too much performance decrease.The DCD iteration is a multiplication-free method to solve the inverse of the matrix and the precision is controlled.The block processing [26]-[29] is also an effective approach to reduce the algorithm computational complexity and it can reach the same convergence rate as the non-block version and smaller computational complexity than the FAP.In[30], the author proposed a parallel computing method which can save the hardware processing time.It is an alternative way to enhance the algorithm implementation in practical.

Based on these ideas, we proposed a block parallell0-SWL-DCD-AP algorithm in this paper.First, to improve the tracking ability of the proposed algorithm, we introduced the shrinkage denoising method to generating a variable step-size, thus the step-size can vary automatically according to the changing of the channel.Second, in order to take advantage of the sparse properties of the channel, we add a zero-attractor to the cost function to count the non-zero number of the channel impulse response.Third, aiming at the non-circular properties of the communication received signals, we exploit the widely linear processing to make full use of the information signals carried.The DCD iterations, block processing, and parallel computing are adopted in proposed algorithm to simply the computation and make it easy for implementation.To fully study the steady-state mean and MSE behavior of the proposed algorithm, we also present the performance analysis of the blockl0-SWLAP algorithm at this work.Simulation results shows that the proposed algorithm can achieve improved performance in the system identification and channel equalization application.

The remainder of this paper is organized as follows.In Section II, we present the system model and rationale of block parallell0-SWLDCD-AP algorithm.In Section III, we analyze the convergence behavior of the proposed algorithm.Numerical results and performance analysis are provided for comparing algorithms in Section IV.Section V drafts the conclusions.

Throughout this paper, the following notations are adopted: Capital boldface letters and small boldface letters are used to denote matrices and vectors, respectively.The superscriptsanddenote the conjugate,inverse operators, transpose and conjugate transpose, respectively.Theandstand for the trace and mathematical expectation of the matrix, respectively.The symboldenotesidentity matrix anddenotes azero vector.The operatorandstand for the absolute value,l0-norm,l1-norm and Euclidean norm, respectively.

I.THE PROPOSED ALGORITHM

Assuming the input vector of the adaptive filter iswherenis the time index andNis the length of the filter.Then the input matrix for AP algorithm iswhereLis the projection order.The noise element isIt is assumed to be the independent and identically distributed (i.i.d.) white Gaussian noise signal with zero mean and variance of.The tap-weight vector of the adaptive filter is

2.1 The block l0-AP algorithm

From [30], we know that the update equation of the blockl0-AP algorithm can be expressed as

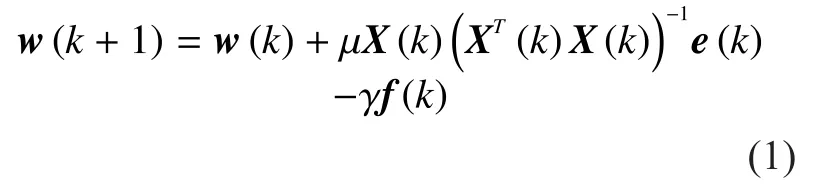
Notice that the time index in the update equation iskat this time.This is because the blockl0-AP algorithm updates the coefficients vector one time everyLiterations,and the actual time index satisfiesis the step-size parameter andis a constant to adjust the weight of the constraint.is the zero-point attraction which is obtained by

A popular approximation forl0-norm constraint [8] is

2.2 The widely-linear processing

In the past, the complex-valued signals is considered circular whose covariance is zero.Although this assumption is convenient, it ignores the second-order properties of the input signals and may lose the information signals carried.

To take full advantage of the phase information, we can adopt the widely linear processing[15].This approach exploits the conjugated form of the signals then the input vector of the filter can be changed as

For the blockl0-AP algorithm proposed in subsection-A, the input signal matrix turns toand its tap-weight update equation is

2.3 The block l0-SWL-AP algorithm

A priorerror vector of the AP algorithm is defined as [7]

where

is the noise-freea priorerror vector.Similarly,a posteriorierror vector is

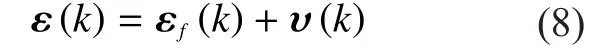
where

is the noise-freea posteriorierror vector.

To demonstrate the relation between the step-size and the estimation error, we can substitute the update equation (5) into (9) and take(6) and (7) into account, then we have

The step-size must be selected to makea posteriorierror vector minimum.We can follow the MMSE principle to minimize the.Taking the expectation of the squared Euclidean norm of (10), we have

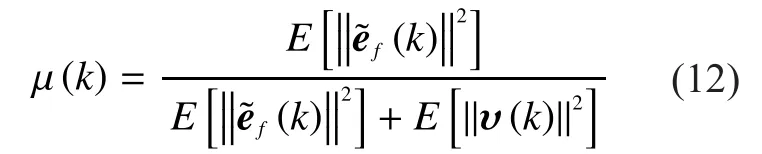
Above is the variable step-size related to thek-th updating.Replacingbyin (5),we will get the update equation of blockl0-SWL-AP algorithm as follows

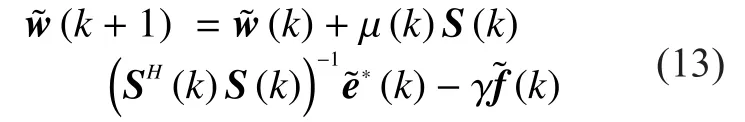
From equation (12) we know that theis decided by theThe former isif the noise is the white Gaussian vector.However, the latter is hard to get because the noise component ofis hard to separate.The shrinkage denoising method used for image denoising problems proposed in [31], [32] can inspire us to solveIt can be expressed as follows

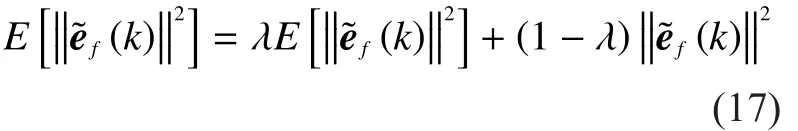
2.4 The block parallel l0-SWL-DCDAP algorithm

The computational of AP-type algorithms mainly originate from its large number matrix operations.The proposed blockl0-SWL-AP algorithm has a complexity ofmultiplications andadditions operations per sample [7].During the derivation of the algorithm, the calculation ofis the largest contribution of the complexity because the inverse operation is complex.Only this operation may require as many asmultiplications andadditions operations per sample.The high complexity is a big obstacle for the hardware implementation of the proposed algorithm.To improve the application of the proposed algorithm, we can utilize the DCD iterations to solve the inverse operations.

The DCD iterations are often used to solve the system of normal equations,The details are present in [33].Assuming the order ofis.We only need predefine three parameters:andwhereis the number of bits corresponding to the binary representation ofandis the limit to the number of the successful iterations.is the amplitude range of the step-sizeα.The parameteris chosen as a power-of-two number, so as toα.After finding the most significant bit ofr, the algorithm starts updaterandThe process is controlled byαwho will reduce tofor less significant bits.After the successful updating of one bit, the algorithm find next significant bit and repeat the above process.During the process, the multiplication operations are replaced by bitshifts and there are only addition operations left.The complexity of DCD algorithm is upper limited bywhile counting comparison operations as addition operations.

For the main computational complexity in the blockl0-SWL-AP algorithm is caused by the calculation of(in Table I isandpdenotes thep-th processors), we can use DCD to solve them.The details can be seen in step 18-27 in Table I.We define thatand[34].After the DCD iterations, the estimate result turns towhich equals to the second term of the tap-weight update equation.The calculationis added into the DCD iterations in step 27.This can reduce the use of multiplication because the calculation ofcan be replaced by bit-shifts [25].With these operations,the computational complexity of derivingand the proposedl0-SWL-DCDAP algorithm isO(L) andO(L2), respectively.

To save the time frequency of the hardware,we can also adopt the parallel implementation in the algorithm application.Assuming there areparallel processors in our work, then we can separately calculate the increment termof thePprocessors at the same time.After the parallel processing, we can sum up all the parallel calculated increments together and add them to the update equation.At this circumstance the tap-weight update equation is calculated everytimes.The details can be seen in step 10-27 in Table I.This approach may reduce the updating times of the tap-weight while keep the convergence and tracking behavior invariant because the up-date increments are the same with the algorithm without parallel processing.Besides, the advantage is obvious because it can reduce the clock frequency bytimes.

Table I The pseudo code of the block parallel l0-SWL-DCD-AP algorithm

III.THE STEADY-STATE BEHAVIOR ANALYZE

As the DCD iterations and the parallel processing are the easy way to apply the algorithm, they do not influence the convergence behavior of the proposed algorithm.So we only analyze the basic blockl0-SWL-AP algorithm in this Section.

3.1 Mean convergence

Considering (6), we have

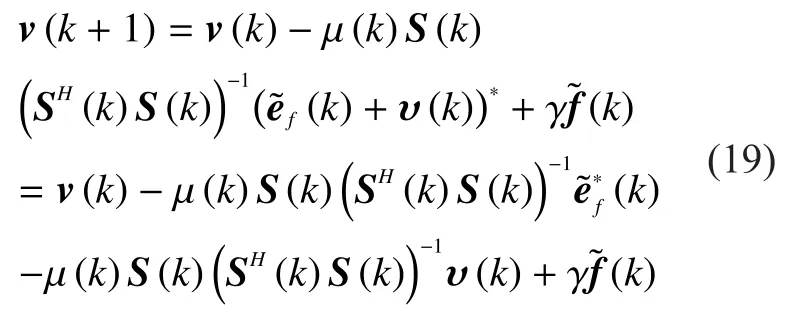
In the front we know that

Substituting (20) into (19), the result follows

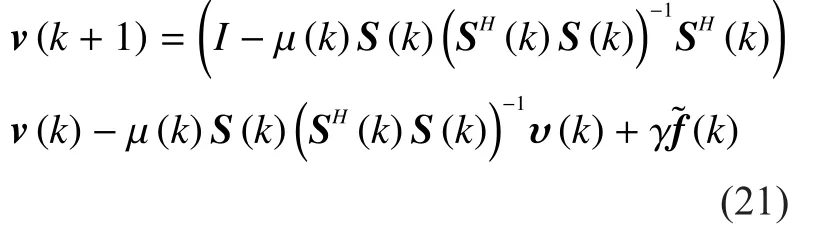
Taking the expectation on both sides, we have

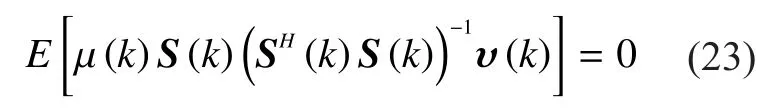
To simplify (22), we can assume thatis independent from each other.Actually the assumption is valid.The details can be derived from (17): whenis close to 1,varies slowly compared withS(k) ande(k).As a result,is approximately uncorrelated withandThen (22)turns to (24) shown in the bottom at this page.

We know that

It is easy to find that the element of (25)achieves

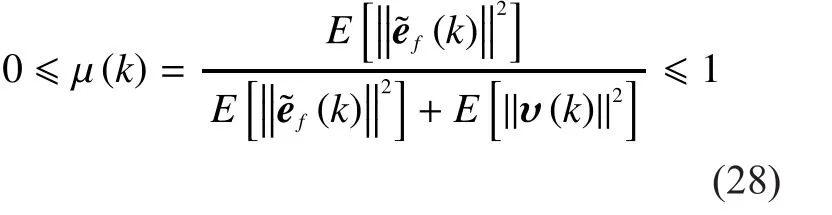
Fortunately, we have and the second term is bounded whenwe can conclude thatis convergent, which meansis closing towhen the algorithm get the steady-state.

so (27) is satisfied easily.

As the first term of (24) is convergent

3.2 MSE Behavior

Evaluating the squared Euclidean norm and then taking the expectation of both sides of(19), rearranging the result, we have (29)shown in the bottom at this page.

To simply the evaluation of the EMSE of the blockl0-SWL-AP algorithm, we can take some identical transformation of (31) as follows

Substituting (32) and (33) into (31) and rearranging the result, we have

Comparing (34) with the result in [37], we can conclude that the first term is the EMSE of standard AP algorithm, while the second term

Fig.1 The learning curve under time invariant sparse system (L=1)

Fig .2 The learning curve under time invariant sparse system (L=4)

is caused by thel0-norm constraint.In [38],we know that ifthe first term is convergent and the second term satisfies

IV.SIMULATION RESULTS

In this section, we demonstrate the advantages of the proposed algorithm comparing with the blockl0-AP algorithm in two adaptive scenarios: sparse system identification and the channel equalization.During the simulations,to make sure the matrix is reversible, a regularization matrixwithis added toEach of the experiment results is averaged over 1000 times to avoid loss the generality.

4.1 Sparse system identification

First we compare the two algorithms under the sparse system identification application.The length of the impulse response of the unknown system is 256.The sparse system is generated by set 16 of the 256 coefficients non-zero and they are randomly distributed.The training sequence is obtained by the zero-mean Gaussian random numbers of unit variance with the length of 500.The noise component is the additive Gaussian noise with zero mean while SNR=10 dB.Thel0-norm constraint parameters are carefully chosen asandFor the block parallell0-SWLDCD-AP algorithm, we chooseandUas the discrete cosine transform matrix[7].The DCD parameters are set asThe parallel sizeis 3.The learning curve is used to compare the convergence rate and the steady-state misalignment of the two algorithms.We use the normalized mean square error (NMSE) which is defined asto normalize the misalignment.The simulation results are presented in Fig.1～ Fig.3.

In Fig.1, we choose the projection orderand the step-size for the blockl0-AP algorithm isAs can been seen in the figure, the proposed block parallell0-SWLDCD-AP algorithm outperforms the blockl0-AP algorithm in both the convergence rate and the final NMSE.The block parallell0-SWLDCD-AP algorithm gets the convergent state after about 150 iterations while the blockl0-AP algorithm convergent after about 250 iterations.Meanwhile, the steady-state NMSE for the block parallell0-SWL-DCD-AP algorithm is -50 dB, which is 30 dB lower than that of blockl0-AP algorithm.This is because the variable step-size brought by the shrinkage linear tracking the system more accurately.When the estimation error is large at the beginning of learning, the step-size is large to accelerate the convergence.After the algorithm is convergent, the small error leads to small step-size to improve the estimation accuracy.So the convergence rate and the steady-state NMSE can be improved at the same time.

In Fig.2, we chose the projection orderand the step-size for the blockl0-AP algorithm is stillFrom the figure we can see that the NMSE gap decrease as the projection order increase.However, the performance of the block parallell0-SWL-DCDAP algorithm is still better than the blockl0-AP algorithm.Comparing with the results in Fig.1, the block parallell0-SWL-DCD-AP algorithm convergent after about 25 iterations whenfaster thanof 150.Besides,the NMSE ofis about 29 dB higher than that ofThat means for the proposed algorithm, the convergence rate improves while the misalignment increases as the projection order increases.Besides, although the parallel processing decreases the learning accuracy in theory, these does not reflect in the simulations as the effect of the shrinkage denoising method is so apparent.

In Fig.3, we change the step-size of the blockl0-AP algorithm toand other parameters remain unchanged.The step-size is chosen carefully to adjust the NMSE performance of block parallell0-SWL-DCD-AP algorithm whose step-size varies through iterations.As can been seen in the figure, when the estimation error is the same, the block parallell0-SWL-DCD-AP algorithm yields nearly a doubled convergence speed compared with the blockl0-AP algorithm.The comparison highlights the advantage of the variable step-size decided by the shrinkage denoising method that it can improve the convergence speed and the steady-state misalignment at the same time.

4.2 Channel equalization

Fig.3 The learning curve for block parallel l0-SWL-DCD-AP algorithm and the block l0-AP algorithm with μ=0.3

Fig.4 The sound velocity profile in South China Sea

In this subsection, we will show the advantages of the proposed algorithm under the area of channel equalization [39].To study the application of the block parallell0-SWL-DCD-AP algorithm, we perform the simulation under the practical channel.The channel is generated by the Bellhop ray tracing program [40]while the.env file is formed by the measured sound velocity profile (SSP) collected in the South China Sea in January.The SSP is depicts in Fig.4.The frequency of the channel is 12 KHz and the symbol rate is 1 kbps.For simplify the simulations, we only choose the real part of the actual impulse response as the experiment channel.The channel is depicted in Fig.5.The transmitted packet contains 500 BPSK training symbols and 2500 BPSK transmitting symbols.The decision feedback equalizer (DFE) is chosen to recover the signal distorted by the channel.The BER is used to measure the result and it is calculated without the training part.

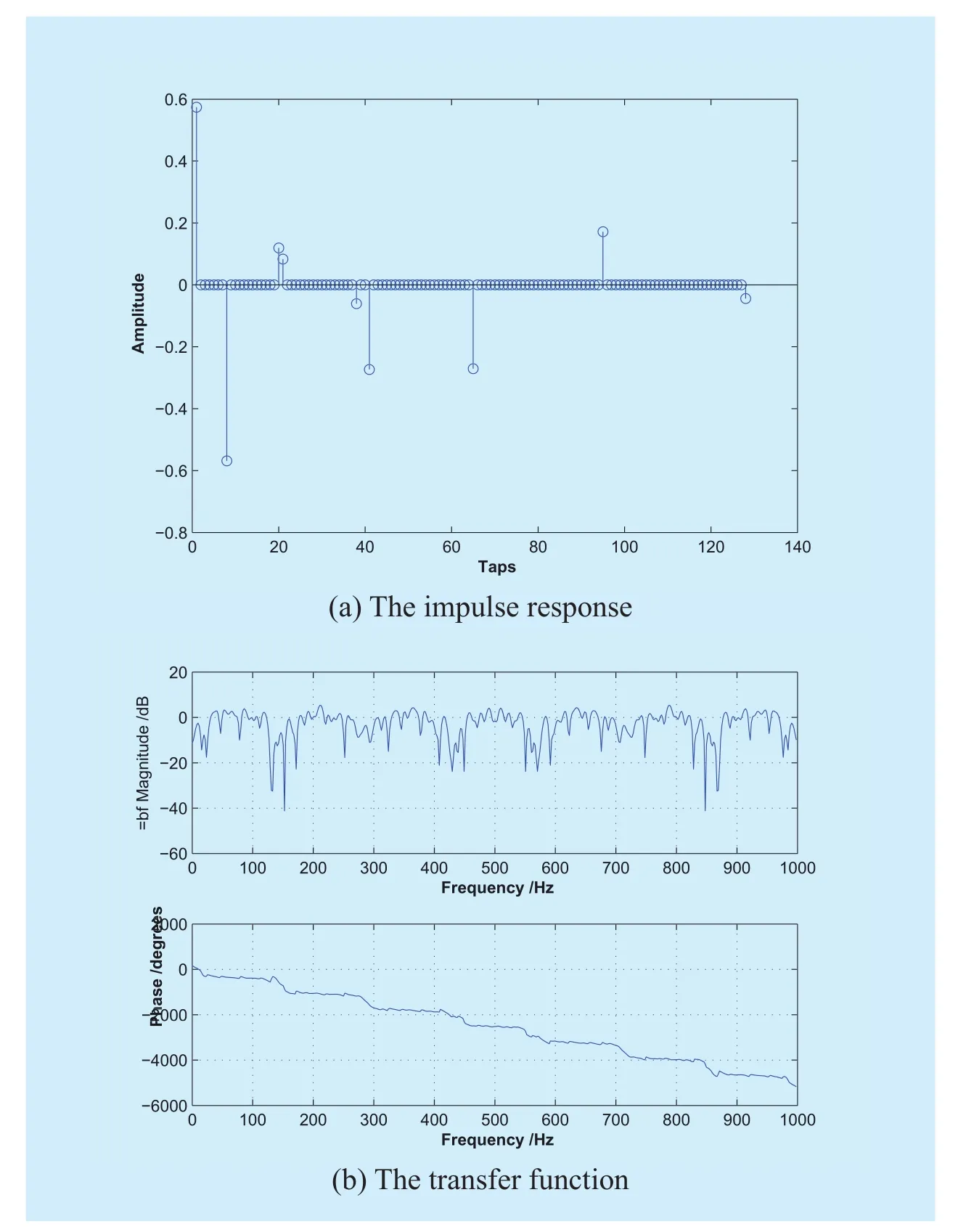
Fig.5 The channel generated by Bellhop

Fig.6 The BER curve of the comparing algorithms

Compared to last subsection, we resetfor the blockl0-AP algorithm,andfor thel0-norm constraint andfor the shrinkage denoising method.The DCD parameters are set asThe projection order isand parallel size isThe result is shown in Fig.6.We can see clearly from the figure that the block parallell0-SWL-DCDAP algorithm achieves the better BER performance than blockl0-AP algorithm.The gap is at least 6 dB when the SNR ranges from 5 to 16 dB.As the SNR increases, the advantage of proposed algorithm gets obvious.The result verifies that the proposed algorithm is suitable for the sparse channel equalization application and it can be applied in the physical truth.

V.CONCLUSION

In this paper, we proposed a block parallell0-SWL-DCD-AP algorithm for the time-varying sparse communication system.The proposed algorithm can not only exploit the sparsity properties of the system, but also provide a variable step-size to track the variation of the different taps.Besides, it utilizes the widely linear processing to make full use of the information the signal carried.As a result, the tracking ability and the estimation accuracy of the adaptive filter are improved.The computational complexity of the proposed algorithm iswhich is lower than theof the non-DCD version.The parallel processing drops the clock frequency of hardware processor to, thus the difficulty of implementation is reduced.Simulations of system identification demonstrate that the proposed algorithm can obtain superior convergence rate and steady-state misalignment performance at the same time and both of them is better than the blockl0-AP algorithm.It can also improve the performance of DFE as the BER after equalization decrease apparently.

ACKNOWLEDGEMENTS

This work was supported by the National Natural Science Foundation of China (Grant No.61471138, 50909029 and 61531012), Program of International S&T Cooperation (Grant No.2013DFR20050), the Defense Industrial Technology Development Program (Grant No.B2420132004), the Acoustic Science and Technology Laboratory (2014).

Reference

[1] F.Albu, C.Paleologu and J.Benesty, “A variable step size evolutionary affine projection algorithm”,IEEE ICASSP, pp 429-432, May, 2011.

[2] F.Albu, C.Paleologu and J.Benesty, “Gauss-Seidel based variable step-size affine projection algorithms for acoustic echo cancellation”,17th European Signal Processing Conference, pp.2007-2011, Aug.2009.

[3] M.Bouchard,“Multichannel affine and fast affine projection algorithms for active noise control and acoustic equalization systems”,IEEE Trans.Speech and Audio Process., vol.11, no.1, pp.54-60, Jan.2003.

[4] J.Benesty, P.Duhamel and Y.Grenier, “A multichannel affine projection algorithm with applications to multichannel acoustic echo cancellation”,IEEE Signal Process.Lett., vol.3, no.2, pp.35-37, 1996.

[5] O.Hoshuyama, R.A.Goubran and A.Sugiyama,“A generalized proportionate variable step-size algorithm for fast changing acoustic environments”,Proc.IEEE ICASSP, vol.4, pp.161-164,2004

[6] C.Paleologu, J.Benesty and S.Ciochina, “A variable step-size affine projection algorithm designed for acoustic echo cancellation”,IEEE Trans.ASLP., vol.16, no.8, pp.1466-1478, Nov.2008.

[7] M.Z.A.Bhotto and A.Antoniou, “A family of shrinkage adaptive filtering algorithms”,IEEE Trans.Signal Process., vol.61, no.7, pp.1689-1697, Apr.2013.

[8] Y.Gu, J.Jin and S.Mei, “l0norm constraint LMS algorithm for sparse system identification”,IEEE Signal Process., vol.16, no.9, pp.774-777, Sept.2009.

[9] Y.Chen, Y.Gu and A.O.Hero, “Sparse LMS for system identification”,Proc.IEEE ICASSP, pp.3125-3128, Apr.2009.

[10] E.J.Candes, M.B.Wakin and S.P.Boyd, “Enhancing sparsity by reweightedl1minimization”,Journal of Fourier Analysis and Applications, vol.14, no.5, pp.877- 905, Dec.2008.

[11] J.Yang and G.E.Sobelman, “Sparse LMS with segment zero attractors for adaptive estimation of sparse signals”,IEEE Asia Pacific Conference on Circuits and Systems,pp.422-425, Dec.2010.

[12] R.Meng, R.C.de Lamare and V.H.Nascimento,“Sparsity-aware affine projection adaptive algorithms for system identification”,SSPD 2011, pp.1-5, Sept.2011.

[13] M.V.S.Lima, W.A.Martins and P.S.R.Diniz,“Affine projection algorithms for sparse system identification”,Proc.IEEE ICASSP, pp.5666-5670, May, 2013.

[14] Q.J.You, Z.Jianyun and Z.Xinan, “A widely-linear LMS algorithm for adaptive beamformer”,IEEE International Symposium on Microwave,Antenna, Propagation and EMC Technologies for Wireless Communications,pp.1060-1063, Apr.2007.

[15] T.Adali, P.J.Schreier and L.L.Scharf, “Complex-valued signal processing: The proper way to deal with impropriety,”IEEE Trans.Signal Process., vol.59, no.11, pp.5101-5125, Nov.2011.

[16] P.Chevalier and F.Pipon,“New insights into optimal widely linear array receivers for the demodulation of BPSK, MSK and GMSK signals corrupted by noncircular interferences-Application to SAIC”,IEEE Trans.Signal Process., vol.54,no.3, pp.870-883, Mar.2006.

[17] P.Chevalier, J.P.Delmas and A.Oukaci, “Optimal widely linear MVDR beamforming for noncircular signals”,in Proc.IEEE Int.Conf.on Acoust.,Speech, and Signal Processing (ICASSP), pp.3573-3576, May, 2009.

[18] P.Chevalier, “Optimal array processing for nonstationary signals”,in Proc.International Conference on Acoustics Speech and Signal Process.(ICASSP), pp.2868-2871, May, 1996.

[19] B.Picinbono and P.Chevalier, “Widely linear estimation with complex data”,IEEE Trans.Signal Process., vol.43, no.8, pp.2030-2033, Aug.1995.

[20] Yun-Mei Shi, Lei Huang, Cheng Qian and H.C.So, “Shrinkage Linear and Widely Linear Complex-Valued Least Mean Squares Algorithms for Adaptive Beamforming”,IEEE Trans.Signal Process., vol.63, no.1, pp.119-131, Jan.2015.

[21] S.L.Gay and S.Tavathia, “The fast affine projection algorithm”,ICASSP, vol.5, pp.3023-3026,May, 1995.

[22] S.L.Gay, “A fast converging, low complexity adaptive filtering algorithm”,in Proc.IWAENC,pp.223-226, 1993.

[23] F.Albu, J.Kadlec, N.Coleman and A.Fagan, “The Gauss-Seidel fast affine projection algorithm”,in Proc.IEEE SIPS, pp.109-114, 2002.

[24] M.C.Tsakiris and P.A.Naylor, “Fast exact affine projection algorithm using displacement structure theory”,in Proc.DSP, pp.69-74, 2009.

[25] Y.Zakharov, “Low-complexity implementation of the affine projection algorithm”,IEEE Signal Process.Lett., vol.15, pp.557-560, 2008.

[26] M.Montazeri and P.Duhamel, “A set of algorithms linking NLMS and block RLS algorithms”,IEEE Trans.Signal Processing, vol.43, pp.444-453, Feb.1995.

[27] C.B.Papadias and D.T.M.Slock, “New adaptive blind equalization algorithms for constant modulus constellations”,in Proc.Int.Conf.Acoustics,Speech, Signal Processing ’94, Adelaide, Australia,pp.321-324, Apr.1994.

[28] S.G.Sankaran and A.A.L.Beex, “Normalized lms algorithm with orthogonal correction factors”,in Proc.31st Annu.Asilomar Conference Signals, Systems, Computers, pp.1670–1673,Nov.1997.

[29] M.Tanaka, S.Makino, J.Kojima, “A block exact fast affine projection algorithm”,IEEE Trans.Speech and Audio Process., vol.7, no.1, pp.79-86, Jan.1999.

[30] D.Yin, H.C.So, Y.Gu, “Sparse constraint affine projection algorithm with parallel implementation and application in compressive sensing”,IEEE ICASSP,pp.7238-7242, May, 2014.

[31] I.Daubechies, M.Defrise and C.De-Mol, “An iterative thresholding algorithm for linear inverse problems with a sparsity constraint”,Comm.Pure Appl.Math., vol.57, no.11, pp.1413-1457,2004.

[32] M.Zibulevsky and M.Elad, “l1-l2optimization in signal and image processing”,IEEE Signal Process.Mag., pp.76-88, May, 2010.

[33] Teyan Chen, “Novel Adaptive Signal Processing Techniques for Underwater Acoustic Communications”, P.h.D.thesis, University of York, Sept.2011.

[34] F.Albu, C.Paleologu, J.Benesty and Y.V.Zakharov, “Variable step size dichotomous coordinate descent affine projection algorithm”,IEEEEUROCON, pp.1364-1369, May, 2009.

[35] H.-C.Shin and A.H.Sayed, “Mean-square performance of a family of affine projection algorithms”,IEEE Trans.Signal Process., vol.52, no.1,pp.90-102, Jan.2004.

[36] G.Su, J.Jin, Y.Gu and J.Wang, “Performance analysis ofl0-norm constraint least mean square algorithm”,IEEE Trans.Signal Process., vol.60,no.5, pp.2223-2235, May, 2012.

[37] Sundar G.Sankaran, A.A.Beex, “Convergence behavior of affine projection algorithms”,IEEE Trans.Signal Process., vol.48, no.4, pp.1086-1096, Apr.2000.

[38] M.V.S Lima, I.Sobron, W.A.Martins and P.S.R.Diniz, “Stability and MSE analyses of affine projection algorithms for sparse system identification”,Proc.IEEE ICASSP, pp.6399-6403, May,2014.

[39] K.Pelekanakis, M.Chitre, “Comparison of sparse adaptive filters for underwater acoustic channel equalization/Estimation”,IEEE ICCS, pp.395-399, Nov.2010.

[40] Orlando Camargo Rodrıguez, “General description of the BELLHOP ray tracing program,” 2007,http://w3.ualg.pt/˜orodrig, orodrig@ualg.pt