Priority-Based Real-Time Stream Coding over Multi-Channel with Packet Erasures

School of Communication and Information Engineering, University of Electronic Science and Technology of China,Chengdu, Sichuan, 611731, China

I.INTRODUCTION

The bandwidth-intensive and delay-sensitive real-time streams are posing increasingly huge burden to various networks [1-4].To provide higher transmission capacity for real-time streams, the scattered resources in different channels can be combined and used together with some efficient coding schemes [5][6].However, to the best of our knowledge,there is no accurate model defining how much resource a real-time stream needs over multi-channel so far.Moreover, given several channels, the transmission capacity for real-time streams and the way to achieve this capacity have not been explored.Therefore,two issues are urgent to be solved:

(i) Modeling the relationship between a real-time stream and the minimum required resource in multi-channel context.Or in another word, exploring the capacity of given channels in transmitting a real-time stream.For brevity, this capacity is denoted asMulti-channel Real-time Stream Transmissioncapacity, orMRSTcapacity.

Table I Shannon capacity versus MRST capacity

Fig.1 An example: MRST capacity is sometimes less than Shannon capacity

(ii) Developing an efficient code to achieve or approach the MRST capacity, which has low computational complexity in encoding and decoding, since increasingly real-time streaming services take place in light mobile devices.

The traditional Shannon capacity cannot accurately specify the MRST capacity under strict delay constraint.A simple example is shown in Fig.1.Suppose the source generates one uniform message every 4 time steps,which should be decoded by the receiver intime steps.Channel 1 can transmit one packet of sizeat each time step,and in every 4 time steps there is one packet erased.For channel 2, the packet size isand in every 2 time steps there is one packet erased.The comparison between Shannon capacity and MRST capacity is shown in Table I.Obviously, the total Shannon capacity iswhich is the essential feature of the channels.Whereas, the MRST capacity changes when the stream changes, and is less than the former in most cases.This leads to the result that traditional coding schemes are not suitable for such real-time streams.

So far only a few works tried to find the transmission capacity for real-time stream and design corresponding codes, which were mostly done over single channel.Leong and Ho [7][8] presented a symmetric intra-session code for real-time streams.Another coding scheme presented by Martinian and Badr in [9][10]can adjust the delay deadline according to the channel quality.Prominent works also have been done in [11][12], where low delay streaming coding schemes over burst and isolated erasures were studied.However, all these works only deal with real-time streams with uniform messages over single channel, and have not considered the multi-channel scenario and the difference in these messages.

The message importance may be different in most streams, such as MPEG-encoded video, where a Group of Pictures (GOP) consists of different types of frames which differ in importance.Under packet erasures, Unequal Error Protection [13], or Priority Encoding Transmission [14], can be used to provide different levels of redundancy protection to messages of different importance, and has been applied to video coding in various literatures e.g.[15][16][17].However, currently prioritized encoding are mostly used in streams without strict delay deadline or the area of source coding.

Therefore, studying the accurate MRST capacity and coding scheme over multi-channel is significant for such prioritized real-time streams.Our previous work [18][19] has done some basic work for this problem, but two limitations exist in that work: (i) only single channel scenarios are considered; (ii) the streams considered in that work are limited into a special kind, which only occupy a small part of all the real-time streams.

The first work deals with the multi-channel issue was done in [20], which only considers the window based erasure channels.In this paper, we extend the work to both window erasure channels and i.i.d.(identically and independently distributed) erasure channels.The contributions are highlighted as follows:

(i) For both window erasures and i.i.d.erasures, we derive the MRST capacity models in multi-channel context.This would help to promote the information theory on real-time stream transmission.At the same time, these capacity models can be used to guide the design of efficient real-time stream coding approaches.

(ii) A Maximum Equilibrium Intra-session Code (MEIC) is proposed for real-time stream over window erasure multiple channels.MEIC can asymptotically achieve the MRST capacities under window erasures, indicating these capacities are tight.

(iii) An Adaptive Maximum Equilibrium Intra-session Code (AMEIC) is proposed for real-time stream over i.i.d.erasure multiple channels, and then proved able to closely approach the MRST transmission capacity upper bound.

I.SYSTEM MODEL

A discrete-time data streaming system is considered, which comprisesκpacket erasure channels from a source to a receiver, as illustrated in Fig.2.

(1) Source.At each time stepthe data source generates a random message.The random variablesare independent and identically distributed, non-positive messagesare zeros.Considering the priorities and sizes of messages in real-time stream usually follow a periodic pattern in practice, this paper assumes that one high priority message is followed bylow priority messages.That is to say, the period is assumed to bewhereHeredis the delay deadline of a message, and.Ifthe messageis a high priority message with sizeotherwise,is a low priority message with size

(2)Coding Window.Letbe the coding window for messagewhich is defined as the interval ofdtime steps between its creation time and decoding deadline, i.e.,The special coding window ofin channelis denoted aswhereLetbe the set of active messages at time step, which include the messages whose effective coding window contains the time step , i.e.,At any time stepa single packetwhich is a function of messages created at or before time step, can be transmitted over channelFor brevity, let

(3) Receiver.In the receiver, each message must be decoded no later than a delay ofdtime steps from its creation time.For example,a messagecreated at time step, is to be decoded by time step.Since this paper deals with hard message decoding deadlines, we use a zero-error decodability condition where a given messageis considered to be decodable from the packets received at time stepsif and only if

Fig.2 Prioritized real-time streaming system for.The source creates one high priority message followed bylow priority messages periodically.Each message must be decoded at the receiver within a delay of d time steps from its creation time.At each time step, packets of sizeare allowed to be transmitted over channelrespectively

(4)Channels and erasure models.Suppose the bandwidth of channelisindicating that at every time stepia packetwith sizecan be sent out.Letdenote the (overlapping)coding windows of the firstmessagesbe the set of erasure patterns for window based erasures of channel, andfor i.i.d.erasures.The erasure models will be demonstrated in detail in corresponding sections.Assumeis the erasure tolerance of messageA messagewith erasure tolerancemeans that for any erasure patterns,if only the ratio (in size) of erased packets incoding window is no more thanthenshould be decodable in the receiver.That is to say,should be decodable with onlyproportion of all packets encodingTherefore,is used to denote the message priority in this paper.For high priority messages there isand for low priority messages there is

(5) MRST capacity.As described above,MRST capacity denotes the transmission ability of given channels for a real-time stream.In the following, in cases there is one message created at each time step, i.e., MRST capacity equals tothe upper bound on message size is treated as an expression of the MRST capacity.

(6) SR stream and AR stream.As defined in [19], the real-time streams are divided into Symmetric Real-time (SR) streams and Asymmetric Real-time (AR) streams, which are briefly introduced as follows.

Definition 1(Symmetric Real-time Stream,SR Stream).Consider a real-time streamwith the corresponding prioritiesin sequence.Given any two time stepstandif the active messages satisfy

such real-time stream is called symmetric real-time stream, or shortened as SR stream.

Definition 2(Asymmetric Real-time Stream, AR Stream).Consider a real-time streamwith the corresponding prioritiesin sequence.If there exists at least one pair of time steptandsatisfies:

such real-time stream is called asymmetric real-time stream, or shortened as AR stream.

III.WINDOW ERASURE MODEL

3.1 Erasure model

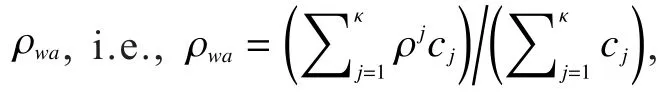
3.2 Symmetric real-time stream

For SR streams under window erasures, a tight MRST capacity exists and can be asymptotically achieved with MEIC-SR, as follows.

3.2.1 MRST capacity for SR stream under window erasures

The MRST capacity for SR streams under window erasures is proposed in a general form where each message can have a different message size and priority, as shown in Theorem 1.Then, the capacity is specialized to the case with two priorities in Corollary 1.

Theorem 1(MRST capacity for SR stream under window erasures).Let a sequence of messagesbe encoded into packetswhereMessageis created at time stepi, packetis the encoded packet in channelat time step, andMessageis decodable at time stepwhenproportion of the packets in its coding windoware unerased.Then in window erasure multiple channels,

Proof:Since there isobviously the right partalways holds.

The left part is proved by contradiction.Assume there is a coding scheme A that encodeswhich satisfies the decoding requirements as well asAggregating theκchannels into one channel with bandwidth, and letting(), the multi-channel problem is degraded into a single channel problem.According to Theorem 1 in [18], there should beHowever,

Then the contradiction is found.Thus, Theorem 1 is proved.

Corollary 1.For the two-priority system with window erasure model in multiple channels, the MRST capacity for SR stream under window erasures is:

Proof:According to the system model,there isandfor high priority messages, otherwiseTherefore, Theorem 1 equals to:

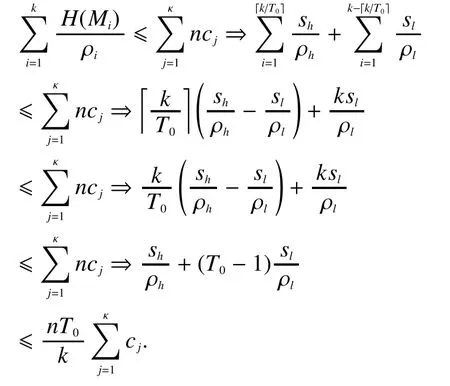
3.2.2 Code construction

In this section, a Maximum Equilibrium Intra-session Code (MEIC) is proposed, which will be shown asymptotically optimal under window erasures.

MEIC is a kind of intra-session code, where coding is allowed within the same message but not across different messages [8].Each packet is partitioned into sub-packets or blocks of possibly different sizes, each encoding a different message.We assume that an appropriate code (e.g., a maximum distance separable (MDS) code or a random linear code) is subsequently applied to this allocation so that each message is decodable whenever the total amount of received data that encodes that message, or the total size of the corresponding blocks, is at least the message sizes.The blocks that encode a given messageare confined to the packets transmitted in the corresponding coding window.Thus, to decode each message, the decoder needs to access only the packets received at the most recentdtime steps.

As illustrated in Fig.3, MEIC divides the packet at each time step into blocks.In the time stepsthe packet in channeljis divided into blocksOtherwise whenthe blocks are

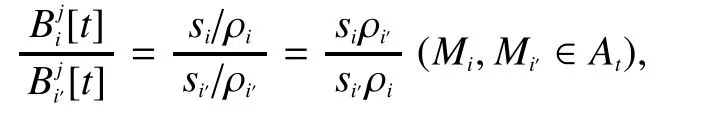
Fig.3 The blocks at each time step in the channels, where cj is the packet size that can be transmitted through channelat each time step

For channelj, there is:

The total size of blocks forat time stepstis:

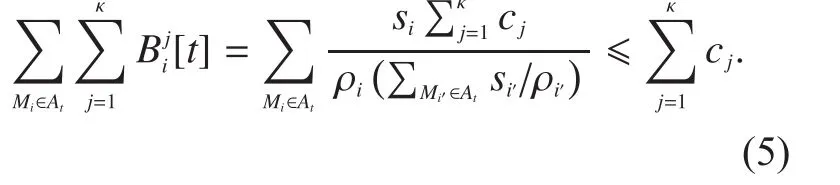
Substituting (4) into (5), we can find (5) always holds.Moreover, for any other time stepaccording to (4),

which means this allocation is appropriate to all time steps.

3.2.3 Achievability

In this part, two lemmas are introduced, based on which MEIC-SR is then shown able to asymptotically achieve the MRST capacity under window erasures when SR stream is considered.

Lemma 1.When MEIC-SR is used in a SR stream described above, there is

Proof:The expressioncan be easily obtained.

Lemma 2.For the SR streams described above, whenthere should be

Proof:According to Theorem 1, there is

Theorem 2(Achievability of MRST capacity for SR stream under window erasures).Consider a SR streamwhereis the amount of channels,is the packets sent out at time stepiin channelj,andMEIC-SR is asymptotically optimal over all codes in the following sense: it achieves a message size of

which is the MRST capacity defined in Theorem 1.

Proof:The proof includes the decodability under given erasure model, and the achievability of MRST capacity.

(1) Decodability.For a messageproportion of the packets are correctly received by the receiver in channelj.Therefore, the total received block size ofis

where (a) follows Lemma 1, step (b) followswhich is the condition in Theorem 2, step (c) follows (4), and (d) follows Lemma 2.

Therefore, according to the feature of intra-session codes, messageis decodable by its delay deadline.is a random selected message, indicating that for all messages in the SR stream, MEIC can ensure the message decodable under given delay and priority constraints.

(2) The achievability of the MRST capacity.To show MEIC-SR can asymptotically achieve the MRST capacity, we need to prove whenthere is

For the left part,

where (a) and (b) follows thatequals to the total size of blocks forin the unerased packets and (4).

Therefore, Theorem 2 is proved.

3.3 Asymmetric real-time stream

In this part, the tight MRST capacity for AR streams under window erasures are derived and shown asymptotically achievable.As described in [19], the capacity for AR streams are much more complicated than SR streams.This is particular true in multi-channel scenarios.To simplify the problem, we focus on the caseand the messages have uniform size,Then, the maximum achievable message size is derived when only intra-session codes are allowed, and this size is shown actually the general MRST capacity for AR streams under window erasures.After that, MEIC-AR is proved able to achieve this capacity.

3.3.1 Maximum achievable message size with intra-session codes

As described above, in intra-session codes,coding is allowed within the same message but not across different messages.Suppose the channels are divided into blocks as shown in Fig.3, which are subsequently allocated to the messages.The allocation should follow two basic rules: i) At each time step of a messagecoding window, there exists one and only one block forin each channel; ii) Each active message of one time step has one unique block at this time step in each channel.

Consequently, there are many possible allocation methods for an AR stream.For example, in channelj, the blocksare allocated to high priority messages andto low priority messages.Letdenote the ratio ofin the blocks of channelfor a high priority message, anddenote that ofthere isandObviously, there isandWe useato denoteandto denote.

Theorem 3.For an AR streamover multiple channels with window erasure modelwhen only intra-session codes are allowed andthe message sizesis upper bounded as:

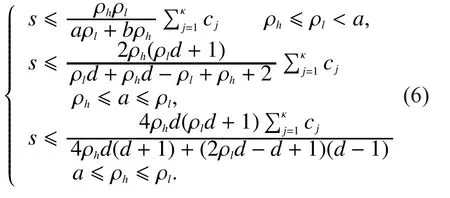
For convenience, the upper bound on message size in theorem 3 is denoted within the following.

Proof:With the two allocation rules described above, the proof will show no allocation methods can exceed the upper bound in Theorem 3 as follows.

Since only intra-session codes are allowed,the channels can be treated as a single channel which can send out a packet with sizeat each time step.Letdenoteand the combined erasure model is

(i) WhenSuppose subsetwhereandSincethere must beTherefore, for high priority messages, there isSumming upfor all possibleV,there is

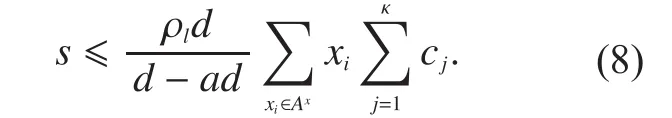
Add up (7) and (8), there is

(ii) Others.Whenorthe following subset should be further introduced:andThen, similar methods can be used to get the result in Theorem 3.

3.3.2 MRST capacity for AR streams under window erasures

The maximum achievable message size derived when only intra-session codes are allowed, is actually the general MRST capacity for AR streams under window erasures, as follows.

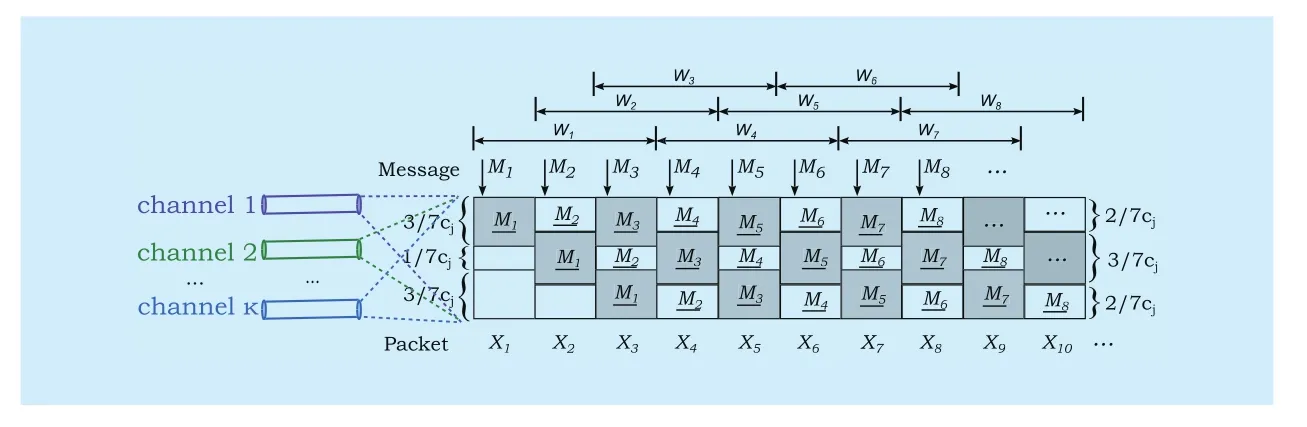
Fig.4 The blocks at each time step in the channels.cj is the packet size that can be transmitted through channelt each time step

Theorem 4 （MRST Capacity for AR Streams under Window Erasures）.For an AR streamover multiple channels with window erasure modelthe MRST capacity is equal to the upper bound when only intra-session codes are allowed.That is, the message sizesis upper bounded as that in Equation (6).Proof:The proof is by contradiction.Suppose there is a coding scheme that can achieve the message sizewhereϵis an infinitesimal positive number.Whenandthere isOn the other hand, sinceportion of packets are erased, the channel capacity can be at mostThis leads to a contradiction.Similarly the other cases can also be shown thatsubis the upper bound on message for all codes.

3.3.3 MEIC for AR streams

For AR streams, we focus on the case(one high priority message is followed by one low priority message) and the messages have uniform size, i.e.,The object of this assumption is to simplify the problem of finding the MRST capacity for AR streams, which is much more complicated than SR streams.The key point of MEIC for AR streams (MEIC-AR) is also the block allocation.Letdenote the upper bound of message size, which has been described in Theorem 4.To achieve this upper bound, the sizes of different blocks are defined as the following:

Fig.4 shows an example of MEIC for AR stream

3.3.4 Achievability

The following result shows MEIC-AR can achieve the MRST capacity in Theorem 4.

Theorem 5.For an AR streamoverκchannels with window erasure modelMEIC-AR can asymptotically achieve the MRST capacity presented in Theorem 4.

Proof:According to MEIC-AR, for a high priority messageMi(i= 1(mod2)), if the weighted packet arrive ratiothe total received blocks size will be distinctly bigger thansub, guaranteeingMidecodable in the re-ceiver.Consequently, we only need to prove the low priority messages are also decodable in the receiver whenever

(i) WhenIn MEIC-AR, the blocks allocated to low priority messages areObviously, according to the block sizes there isTherefore, the total size of received blockswill be:

Therefore, the low priority messages are decodable in the receiver.

(ii) Others.For the other two casesandwith similar method, the low priority messages can also be shown decodable in the receiver whenever

Consequently, Theorem 5 is proved.

IV.I.I.D.ERASURE MODEL

For i.i.d.erasure models, each packet transmitted over a channel is erased identically and independently distributed with a specific probability.Let the erased probability in channelbe denoted withand received probability with

In the window erasure channels, we can use MEIC-SR or MEIC-AR to ensure the messages decodable under given conditions.Whereas,in the i.i.d.erasure channels, even if the packet erasure rate is very low, there is a probability that most (or even all) packets encoding one message are erased.That is to say, we cannot ensure any message decodable, unless we are using ideal channels without packet erasure.Therefore, instead of directly using message priority, we specify a desired recovery probabilityfor each messageFor the two-priority streaming system we consider

In this section, the size of channels are set as uniformc, i.e.,which is common in practice and can decrease the complexity in defining or applying the MRST capacity.The SR streams and AR streams are analyzed together, since they make no essential difference under i.i.d.packet erasures.

4.1 MRST capacity under I.I.D.erasures

To satisfy the desired recovery probabilityfor high priority messages andfor low priority messages simultaneously, we develop an upper bound on the messages’ sizes for the class of time-invariant codes.

Theorem 6.Consider the i.i.d problem with given values ofFor any time-invariant code with finite encoder memory sizethe high priority message sizeand low priority message sizemust satisfy

Proof:As shown in Fig.5, one message is decodable under some erasure patterns,and undecodable under others.Letdenote all of the time steps that are no later than the decoding deadline for message, and the random subsetbe the unerased time steps in channelj; the received packets that can be used by the decoder for decoding messageare therefore given byConsequently, the decoding probabilitywherecan be expressed in terms ofas follows:

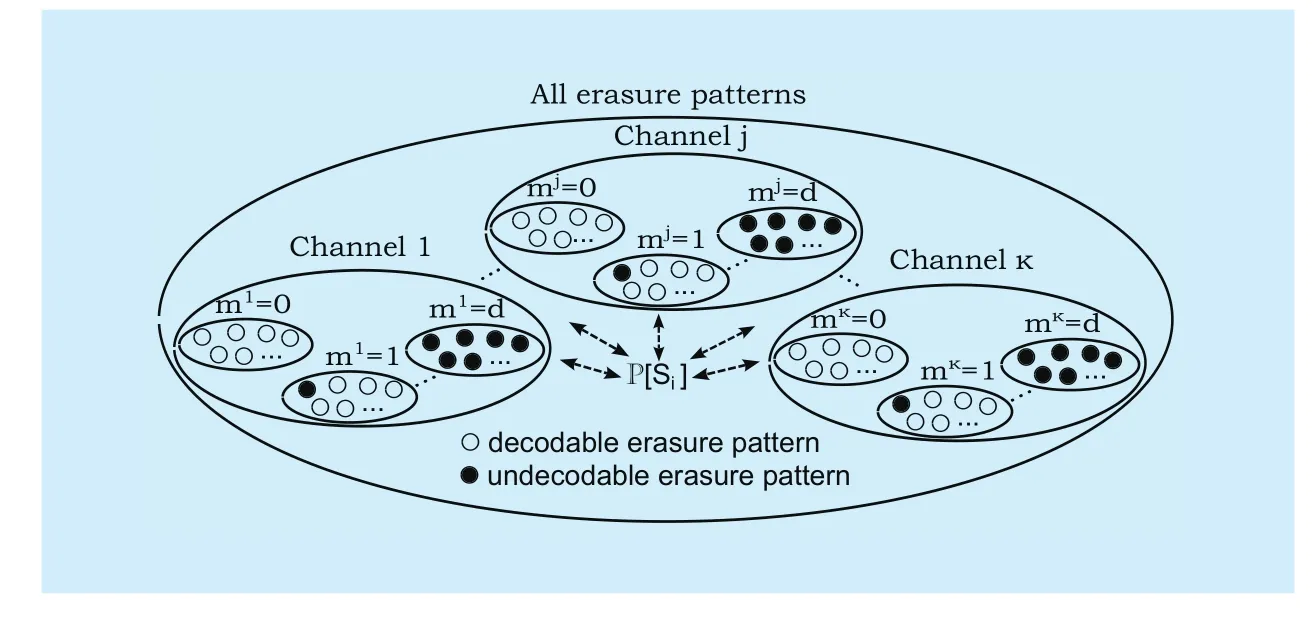
Fig.5 All possible erasure patterns.m denotes the number of erased packets in a message’s coding window over the corresponding channel.The message is decodable under some erasure patterns, and undecodable under others.The decodability of an erasure pattern in one channel should be judged together with the erasure patterns in the other channels

By partitioning the set of unerased time stepsinto two sets(i.e., unereased time steps before the coding windowand(i.e., unerased time steps in the coding windowafter some derivation from (9), we can upper boundas:

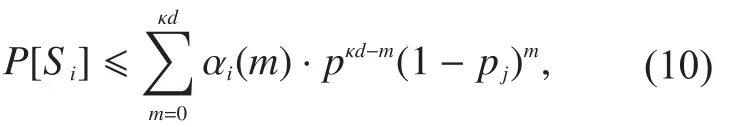
where

For the class of time-invariant codes that we consider, for anythere is

By a conditional entropy based derivation fromwe can also have:

The result follows combining (10), (11) and(12).

4.2 Code construction

To approach the MRST capacity as close as possible, we propose an Adaptive Maximum Equilibrium Intra-session Code (AMEIC),which is enhanced from MEIC, as follows.

AMEIC also divides the packet at each time step into blocks, but the division and allocation in AMEIC are different from that in Fig.3.As shown in Fig.6, all the channels are sorted in the descending order ofp.This is to say, after ordering, channel 1 is the best channel with the lowest erasure probabilitythen channel.Or in another word, after ordering there isAt each time step, the best channels should be firstly allocated to the high priority active messages.After these messages are satisfied,the left channels are divided and allocated to the low priority active messages.In the messages of the same priority, the earlier message can be allocated prior to the later ones, so that the earlier messages may have better channels.

Therefore, in each time step, AMEIC will allocate the channels to the active messages according to the following steps:

Step 1:Sort all available channels in the ascending order of erasure probabilityand denote the sorted channels as channelwith the channel capacity

Step 2:Sort all active messages according to the descending order of priority.In the same priority, earlier message is prior to later message.For brevity, denote the sorted messages asand their priorities asis a high priority message,otherwise,

Fig.6 The block division and allocation in AMEIC.In this figure we assume the stream is

Step 3: Allocate the blocks to messageThe allocation begins from the best available channel — channel 1.If channel 1 is not enough, then some block in channel 2 will be allocated, and so on.Letdenote the blocks allocated toin channelj, then messagehas blocksNote that if channel 1 is enough forthere isandOtherwise,and AMEIC will continue to allocate block in the subsequent channels.The total block size allocated tocomply with the following equation:

Step 4:In the rest available channels, repeat the operation in step 3 to messagesuntil all messages are allocated with appropriate blocks.

Step 5:Apply some appropriate code (e.g.,a MDS code or a random linear code) to this allocation.Form the blocks in each channel into a packet and send out this packet.

According to equation (13), it is easy to deduce that the total size of all allocated blocks just equals to

4.3 Achievability

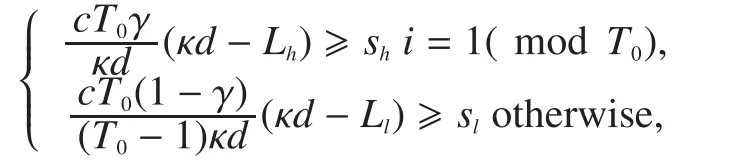
Proposition 1.For the i.i.d.problem with given conditionsandAMEIC can achieve a message size of

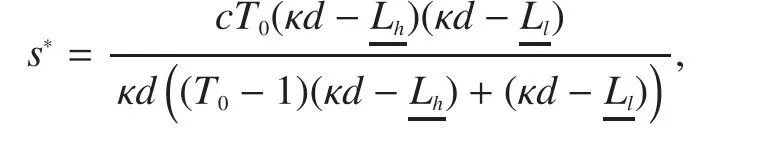
with the allocation ratio

where

Proof:Note thatandare the minimum values ofandrespectively such that the required decoding probabilities are satisfied.From (14), the message sizesand allocation ratioshould satisfy

When gets the optimal value, we should have

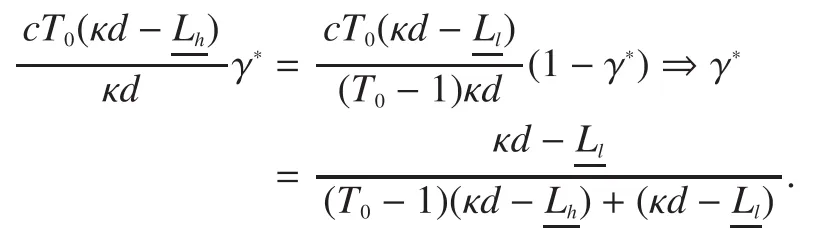
Therefore, the optimal messages size under MEIC is

Fig.7 The achievability of MEIC for SR streams comparing to the MRST capacity over two window erasure channels, where(Byte).Two SR streams are considered: stream 1and stream 2

Comparing the message size in Theorem 6,we can find there is a gap between them.But this gap decreases asandbecome closer ordgoes to infinity.

V.PERFORMANCE EVALUATION

Although the MRST capacities and the achievability of MEIC or AMEIC have already been proved theoretically, the performance evaluation is shown in this section, so as to provide an intuitionistic and practical demonstration.

The performance evaluation of MEIC for SR streams (MEIC-SR) is shown in Fig.7.In the first dozens of time steps, there is a gap between MEIC-SR and the MRST capacity.But this is a transient state, no optimization is needed to be done to reduce the gap.With the time steps increasing, the gap quickly becomes 0.Consequently, the performance evaluation shows that MEIC-SR can asymptotically achieve the MRST capacity for SR streams over multiple channels with window erasures.

The performance of Symmetric Time-invariant Intra-session Code (STIC) from [7]is also compared in Fig.7.Since STIC is proposed for real-time stream with uniform messages, for STIC we setAs shown in Fig.7, the maximum achievable message size with STIC isBytes, but with MEIC, there isBytes whenBytes, andBytes whenBytes, which is much better than STIC for such streams.

The performance evaluation of MEIC for AR streams (MEIC-AR) is shown in Fig.8.Apparently, the capacity defined in Theorem 1 is loose for AR streams.The MRST capacity is evaluated when the time stepsince the streams are in transient state in the first dozens of time steps.As shown in Fig.8, whencan asymptotically achieve the MRST capacity for AR streams over multiple channels with window erasures.Moreover,MEIC-SR and STIC are also evaluated for AR streams.Obviously, MEIC-AR is distinctly better than STIC and MEIC-SR.

For i.i.d.erasures, the maximum message sizes of AMEIC, STIC and the MRST capacity are shown in Fig.9.AMEIC can achieve bigger message size than STIC, which has to treat all messages with the high priorityWhen the gap betweenandbecomes larger, the gap between AMEIC and STIC becomes larger too.At the same time, there is a gap between AMEIC and MRST capacity of the real-time stream over multiple channels with i.i.d.erasures.This gap decreases asandbecome closer ordgoes to infinity.

VI.CONCLUSION

In this paper, the concepts of Symmetric Real-time streams and Asymmetric Real-time streams are introduced.To solve the problem that traditional capacity theories cannot cover multi-channel real-time streams, the MRST capacity models are derived for SR streams and AR streams respectively under window erasures.These models would help to promote the information theory on real-time stream transmission, and be used to guide the design of efficient real-time stream coding approaches.Theoretical analysis and simulation results show the MRST capacities of SR streams and AR streams are both asymptotically achievable by the proposed coding scheme MEIC.Moreover, the MRST capacity under i.i.d.erasures is also derived in the form of recovery probability constrained maximum message size.AMEIC is proposed to be applied to the case under i.i.d.erasures.The simulation results show AMEIC can approximately approach the MRST capacity under i.i.d.erasures.

ACKNOWLEDGEMENTS

This work has been supported by National Key Technology Research and Development Program of China under Grant No.2015BAH08F01, and the joint fund of the Ministry of Education of People's Republic of China and China Mobile Communications Corporation under Grant No.MCM20160304.

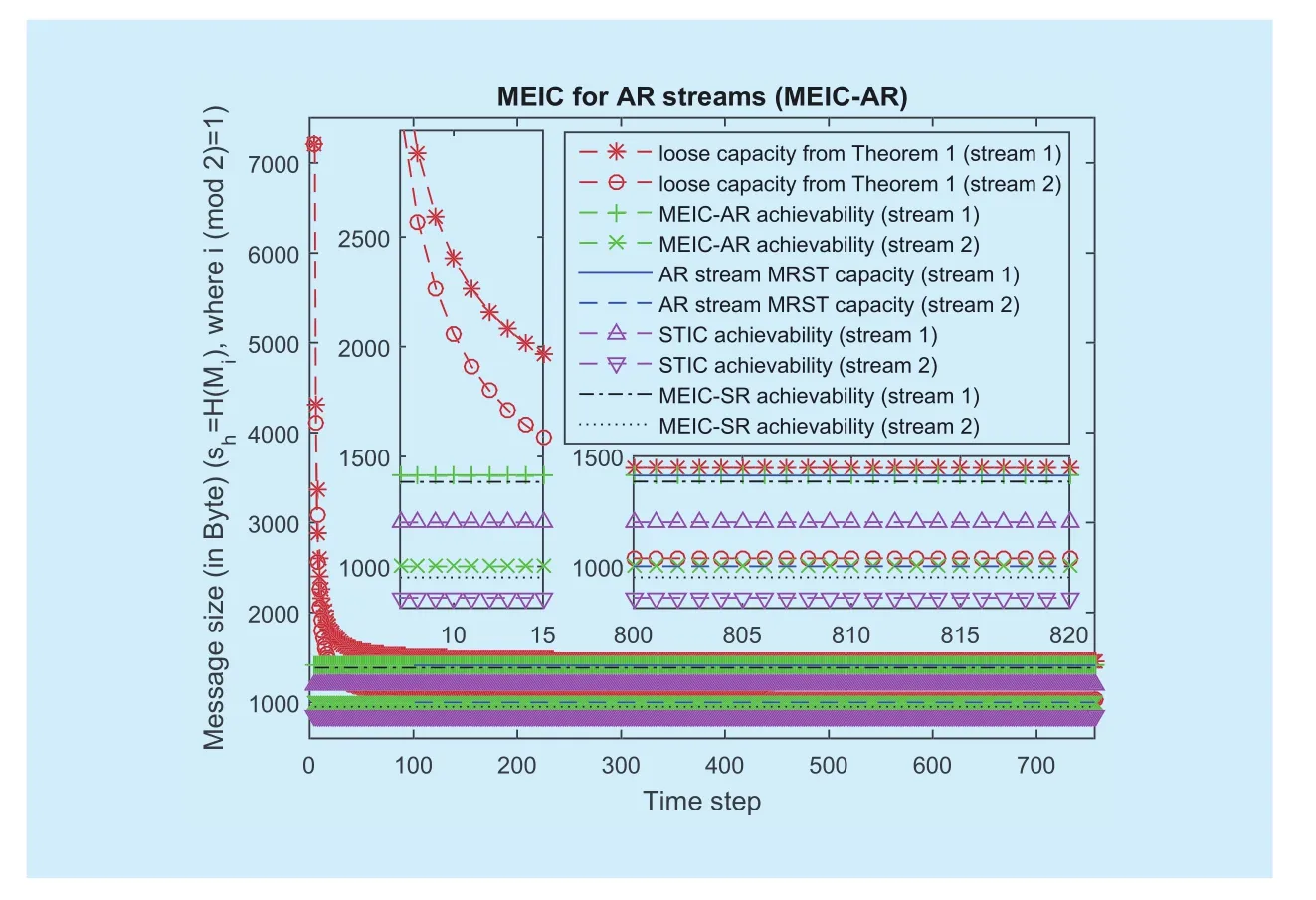
Fig.8 The achievability of MEIC for AR streams comparing to the MRST capacity over two window erasure channels, where c1 = 1000 and c2 = 2000 (Byte).Two AR streams are considered: stream 1(d,T0,ρh,ρl) = (5,2,2/5,3/5); and stream 2(d,T0,ρh,ρl)= (7,2,2/7,3/7)

Fig.9 The maximum message size that AMEIC can achieve over two i.i.d.erasure channels with the same packet erasure probability, where c1 = c2 = 1000 Bytes.The result is compared with that in the existing non-prioritized STIC scheme and the MRST capacity.The considered real-time stream is (d,T0,rh,rl) = (20,2,0.99,0.9)

[1] “Cisco visual networking index: Global mobile data traffic forecast update, 2015-2020 white paper”,tech.rep.,Cisco, February 2016.

[2] G.Nan, Z.Mao, M.Li, Y.Zhang, S.Gjessing,H.Wang, and Mohsen Guizani, “Distributed Resource Allocation in Cloud-based Wireless Multimedia Social Networks”,IEEE Network Magazine, vol.28, no.4, pp.74-80, August 2014.

[3] G.Nan, Z.Mao, M.Yu, M.Li, H.Wang, and Y.Zhang, “Stackelberg Game for Bandwidth Allocation in Cloud-based Wireless Live-streaming Social Networks”,IEEE Systems Journal, vol.8,no.1, pp.256-267, March 2014.

[4] T.Jiang, H.Wang and Y.Zhang, “Modeling Channel Allocation for Multimedia Transmission over Infrastructure based Cognitive Radio Networks”,IEEE Systems Journal, special issue on Multimedia Communications Systems, vol.5,no.3, pp.417-426, Sept.2011.

[5] S.Maharjan, Y.Zhang, and S.Gjessing, “Optimal Incentive Design for Cloud-enabled Multimedia Crowdsourcing”,IEEE Transactions on Multimedia, Vol.PP, no.99, pp.1-11, August 2016.

[6] Z.Mao, G.Nan, and Y.Zhang, “Game-theoretical Approaches in Wireless Multimedia Social Networks”,IEEE MMTC (Multimedia Communications Technical Committee) E-Letter, 2012.

[7] D.Leong, A.Qureshi, and T.Ho, “On coding for real-time streaming under packet erasures”,in IEEE International Symposium on Information Theory (ISIT), (Istanbul, Turkey), pp.1012-1016,July 2013.

[8] D.Leong and T.Ho, “Erasure coding for real-time streaming”,in IEEE International Symposium on Information Theory (ISIT), (Cambridge,MA), pp.289-293, July 2012.

[9] E.Martinian and C.-E.W.Sundberg, “Burst erasure correction codes with low decoding delay”,IEEE Transactions on Information Theory, vol.50,pp.2492-2502, October 2004.

[10] A.Badr, A.Khisti, and E.Martinian, “Diversity embedded streaming erasure codes (de-sco):Constructions and optimality”,IEEE Journal on Selected Areas in Communications, vol.29,pp.1042-1054, May 2011.

[11] A.Badr, A.Khisti, W.-T.Tan, and J.Apostolopoulos,“Streaming codes for channels with burst and isolated erasures”,in 2013 Proceedings IEEE INFOCOM, (Turin, Italy), pp.2850-2858, April 2013.

[12] A.Badr, A.Khisti, W.tian Tan, and J.Apostolopoulos, “Streaming codes with partial recovery over channels with burst and isolated erasures”,IEEE Journal of Selected Topics in Signal Processing, vol.9, pp.501-516, January 2015.

[13] B.Masnick and J.Wolf, “On linear unequal error protection codes”,IEEE Transactions on Information Theory, vol.IT-13, no.3, pp.600-607, 1967.

[14] A.Albanese, J.Blomer, J.Edmonds, M.Luby,and M.Sudan, “Priority encoding transmission”,IEEE Transactions on Information Theory, vol.42,pp.1737-1744, November 1996.

[15] R.Janakiraman and L.Xu, “Layered priority encoded transmission for video streaming to heterogeneous clients”,in International Symposium on Information Theory (ISIT), (Chicago, IL),pp.331, June 2004.

[16] Q.Qu, Y.Pei, and J.W.Modestino, “An adaptive motion-based unequal error protection approach for real-time video transport over wireless ip networks”,IEEE Transactions on Multimedia, vol.8, pp.1033-1044, October 2006.

[17] K.-C.Yang and J.-S.Wang, “Unequal error protection for streaming media based on rateless codes”,IEEE Transactions on Computers, vol.61,pp.666-675, May 2012.

[18] Y.Wei and T.Ho, “On prioritized coding for real-time streaming under packet erasures”,in 51st Annual Allerton Conference on Communication, Control, and Computing, (Monticello,USA), pp.327-334, October 2013.

[19] Y.Wei, Y.Mao, S.Leng, and T.Ho, “Priority-based real-time stream coding under burst erasures”,in 2015 IEEE Global Communications Conference, (San Diego, CA), pp.1-7, December 2015.

[20] Y.Wei, Z.Hu, Y.Mao, and S.Leng, “Priority-based real-time stream coding over multi-channel under sliding window erasures”,in fifth IEEE/CIC International Conference on Communications in China, (Chengdu, China), pp.1-7, July 2016.