Hybrid Gene Expression Programming-Based Sensor Data Correlation Mining

Lechan Yang, Zhihao Qin, Kun Wang, Song Deng

1 International Institute for Earth System Science, Nanjing University, Nanjing 210093, China

2 Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing 100081, China

3 Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks, Nanjing University of Posts and Telecommunications,Nanjing 210023, China

4 Institute of Advanced Technology, Nanjing University of Posts and Telecommunications, Nanjing 210023, China

* The corresponding author, email: kwang@njupt.edu.cn

I.INTRODUCTION

The model mining based on hyperspectral sensor data is an important branch of data processing.Extracting useful knowledge from high-dimensional, complex hyperspectral sensor data is critical for the application of sensor data in a wide range of industries [1-10].The traditional method of model mining based on hyperspectral sensor data is field sampling and laboratory determination.However, this method is error-prone and time consuming in terms of sampling, measurement and data analysis.In many model mining applications based on hyperspectral sensor data, reflectance estimation model mining of leaf nitrogen concentration (LNC) is most important.As the variation of LNC may affect the leaf physiological characteristics of the internal organization and cause the specific reflectance spectral trait to change, the assessment of LNC can be conducted by establishing the model between reflectance spectrum and LNC.Many studies have focused on establishing the relationship between LNC or canopy nitrogen concentration and spectral bands or the derived spectral indices [11-18].However, most of the regression methods [19, 20] depended on a priori knowledge and many subjective factors.Meanwhile, these methods have high time complexity and low computational efficiency for complex and high-dimensional hyperspectral data.In this paper, we propose an algorithm called hybrid gene expression programming for LNC reflectance estimation using hyperspectral data.The major contributions of our work are listed as follows:

(1) For hyperspectral sensor data, most of the dimensionality reduction methods give priority to regression methods.These methods inevitably result in the loss of part of the decision information in hyperspectral data.However, the Rough Set (RS) does not change the decision rules of the original hyperspectral data.In this paper, we present a novelty dimensionality reduction algorithm with noise data based on dependence degree (DRNDDD) to find the optimal hyperspectral band.

(2) The traditional estimation model mining algorithms between LNC and hyperspectral band depended on prior knowledge.This would lead to the traditional estimation model having too much subjectivity.Based on the dimensionality reduction of hyperspectral band,we apply gene expression programming to mine the estimation model between LNC and hyperspectral band.

The remainder of this paper is organized as follows.In Section II, we briefly describe the related work.In Section III, we introduce the dimensionality reduction algorithm with noise data based on the dependence degree.In Section IV, we propose reflectance estimation model mining of LNC for hyperspectral data based on hybrid gene expression programming.Simulation results are provided in Section V and VI, and we conclude this paper in Section VI.

II.RELATED WORK

2.1 Model estimation of LNC

Yao et al.[12] indicated that the sensitive spectral bands for leaf nitrogen concentration (LNC) in wheat existed mainly within the visible and near-infrared regions.Three spectral indices were found to be best for estimating LNC in wheat, and the regression models based on these spectral indices were established.Wang et al.constructed the new spectral index for LNC estimation based on the available index and correlation analysis.Then, the linear regression model between LNC in rice and wheat and new spectral index was built [15].Sun et al.employed the BP network, LM neural network and Bayesian neural network to build a spectrum model for the estimation of LNC in rice.He suggested that the LM neural network is the best in terms of prediction accuracy [11].Zhai et al.compared partial least squares regression (PLSR) and support vector machine regression (SVMR)methods for estimating LNC in leaves of diverse plants using visible and near-infrared reflectance spectra [17].He indicated that the SVMR method achieved better estimation accuracies and has the potential to estimate LNC.Du et al.[21] estimated rice leaf nitrogen contents based on hyperspectral LIDAR by using support vector machine (SVM) regression.The results showed that the method could help farmers make more accurate fertilization strategies.Kalacska et al.[22] estimated foliar nitrogen content from hyperspectral data by using a model insensitive to plant functional type.For nitrogen status estimation,Sumriddetchkajorn et al.[23] proposed a single-wavelength-based rice leaf color analyzer.These methods can be used to estimate LNC.However, these traditional regression methods depended on a priori knowledge and many subjective factors.Moreover, these methods have high time complexity and low computational efficiency for complex and high-dimensional hyperspectral data.

To solve these problems, Koza et al.used genetic programming (GP) for a mathematical model and obtained good experimental results [24].At the same time, GP also avoided the defect in traditional statistical methods of selecting the function model in advance.However, the efficiency of the function model that was mined by GP was low.Thus, a new algorithm, which was called gene expression programming (GEP), was advanced by Portuguese biologist Ferreira in 2001 [25, 26].Compared with GP, the efficiency of complex function mining based on GEP was increased by 4-6 times.

2.2 Gene expression programming

In this study, the gene expression programming (GEP) algorithm was employed to estimate LNC in various plants using hyperspectral band.GEP is an evolutionary algorithm for model learning or formula discovery from data [27, 28]; it uses a search and optimization technique to solve a particular problem by randomly generating expressions that are coded as a tree structure.A best solution is reached based on the fitness of expressions.For GEP,when establishing an estimation model between LNC and hyperspectral band, there is no need for prior knowledge.To date, a wide range of GEP applications in resources assessments and environment modeling have been reported [29-33].

Moreover, Yassin et al.introduced gene expression programming into a predictive model for furrow irrigation infiltration [34].The comparison results showed that GEP has obvious advantages compared with traditional algorithms.Zorn et al.proposed a peak flood estimation model based on gene expression programming in comparison to the Regional Flood Estimation (RFE) method [35].Yassin et al.estimated daily reference evapotranspiration in an arid climate by using artificial neural networks and gene expression programming,respectively [36].Dey et al.[37] used gene expression programming to predict the heat transfer characteristic.The results showed that the heat transfer rate of a circular cylinder could be enhanced.

In all of the latest works, gene expression programming is an inspiring algorithm.This shows that gene expression programming has a powerful function model mining and is well suited to build the nonlinear model between LNC and hyperspectral band.

2.3 Dimensionality reduction of hyperspectral data

Moreover, dimensionality reduction of hyperspectral data should be taken into account when these methods are used to estimate LNC.Hyperspectral data usually consists of hundreds or even thousands of narrow, continuous spectral bands [38, 39].Many adjacent bands have strong correlation and contain redundant information [40-42].Thus, reducing the dimensionality of hyperspectral data is necessary.Before building linear regression models,the correlation analysis method was always used to select the optimal hyperspectral wavebands in previous studies [12, 15].Principal component analysis (PCA) was also employed to reduce the dimensionality of hyperspectral data when using a neural network algorithm[43].Another wavebands selection technique was the stepwise regression method [44].

Although there are various methods for reducing the dimensionality of hyperspectral data,so far, the optimal wavebands for estimating LNC in various plants have not been settled.These dimensionality reduction methods of hyperspectral data inevitably result in the loss of part of the decision information, while dimensionality reduction based on the rough set(RS) [45] does not change the decision rules of the original data set.

II.DIMENSIONALITY REDUCTION ALGORITHM WITH NOISY DATA

In this section, we will introduce the rough set into the dimensionality reduction with noisy data.

3.1 Preliminaries

Hyperspectral data are very large and of high dimensionality.Many bands are redundant due to the strong correlation between bands that are adjacent.Hence, the analysis of hyperspectral data is complex and needs to be simplified by selecting the most relevant spectral bands [46].Therefore, to establish the model between LNC and hyperspectral band, the first thing to do is to analyze the hyperspectral data.Usually, hyperspectral data of all crops,trees and other plants includes thousands of spectral attributions.To better describe hyperspectral sensor data, the hyperspectral data decision table is defined as follows.

Definition 1.Let the data table bewhereandrepresent the hyperspectral data set, hyperspectral band, level of leaf nitrogen content, set of hyperspectral band, and leaf nitrogen content value and information function, respectively,andData tableis called the hyperspectral data decision table.

To understand the dimensionality reduction algorithm of hyperspectral data based on a rough set, we shall first briefly introduce the related concepts for a rough set in this paper [45].

Definition 2.Let the hyperspectral data decision table beandif and only if; then,andare indiscernible and denoted by

Definition 3.Let the hyperspectral data decision table beThe positive region

Definition 4:Let the hyperspectral data decision table beFor the same condition attributes value, the corresponding decision attribute value is also the same.Hyperspectral data decision tableis consistent.

Definition 5:Let hyperspectral data decision tablebe consistent.The dependence degree between condition attributionand decision attributionis denoted byForifthen condition attributionis reducible, whererepresents the number of elements in hyperspectral data set.

3.2 Algorithm description

To better mine the model between LNC and hyperspectral band by using GEP, the reduction of hyperspectral band must be performed to decrease computational complexity.However, in the process of data acquisition during crop monitoring, much noisy hyperspectral data are generated due to the human, network or collecting device.Attribution reduction for the hyperspectral data with noise is bound to affect the accuracy of reduction, which will eventually lead to the precision of the LNC estimation model.Accordingly, it is necessary to find and remove the noise data in the process of attribute reduction.This can reduce the effect of noise during the attribute reduction.In this paper, a novelty dimensionality reduction algorithm with noisy data based on dependence degree (DRND-DD) is proposed.

Before reduction, we first find the noise data detection algorithm based on the nearest distance (NDD-NearDis).The algorithm can find the noise data without prior knowledge and delete the noise.First, the definition of noise data is given.

Definition 6.Letbe the distance threshold,be the fraction threshold, andbendata.Ifthen data objectuiis called noise data.

The noise data detection based on the nearest distance (NDD-NearDis) is as follows.

Based on algorithm 1, we suppose that the hyperspectral data decision table is consistent.Then, hyperspectral data feature attribution can be reduced by calculating the dependence degree between hyperspectral band and the level of leaf nitrogen contents.The flow of DRND-DD is as follows.

Time consumption of the entire algorithm mainly occurs when calculating the dependence degreeof each hyperspectral band.Thus, the time complexity of the algorithm is approximately

IV.REFLECTANCE ESTIMATION MODEL MINING OF LNC

4.1 Algorithm overview

Essentially, reflectance estimation of LNC is to build a nonlinear function model mining between LNC and hyperspectral band.In terms of model mining, reflectance estimation of LNC can be perceived as a process that establishes a model between LNC and hyperspectral band and that determines reflectance estimation of LNC based on the model.Traditional regression methods are applied to the estimation of the biochemical contents of plants.Multiple linear regression (MLR) has been applied to estimate the LNC [13, 47, 48].Partial least squares regression (PLSR) and support vector machine regression (SVMR)are regarded as effective in estimating the leaf nitrogen content of plants [17, 49].Elfatih M.Abdel-Rahman et al.applied random forest regression to estimate the LNC [17].These methods depend on a priori knowledge and several subjective factors; thus, the complex function model is not easy to build.Meanwhile, these methods assume that the model type between LNC and hyperspectral band is known in advance.To solve these problems,based on DRND-DD, reflectance estimation model mining of LNC for hyperspectral data based on hybrid gene expression programming(REMLNC-HGEP) is proposed in this paper.

4.2 Coding of REMLNC-HGEP

Coding of GEP is an important expression form of REMLNC-HGEP.To explain the coding of REMLNC-HGEP, the relevant definitions are as follows.

Definition 7.Let the function set beand terminal set bewheremrepresents the number of hyperspectral band.Then, the gene that is built according to the rules and symbol in Ref.[26] is called estimation of theLNC gene (ELNC-Gene).

Algorithm 1: NDD-NearDis (HT)

Algorithm 2: DRND-DD (HT)

The head of the ELNC-Genehcomprises elements ofFandT, while the tail of ELNC-Genetcomprises elements ofT.Moreover,the lengths ofhandtfollow the equation:

wherenrepresents the maximum number of arguments of the operator in the gene head.

Fig.1 A random chromosome in GEP

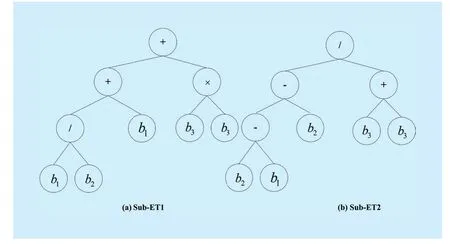
Fig.2 The corresponding ETs

REMLNC-HGEP adopts linear code of fixed length to represent an individual called a chromosome [50].A chromosome is composed of one or more ELNC-Gene(s).However, the linear code can accurately show expression trees (ETs) of different shapes and sizes.During decoding, ETs are traversed from the top to the bottom, from the left to the right.Finally, the function model is obtained.The following example 1 illustrates the coding and decoding of REMLNC-HGEP.

Example 1:Let the function set beterminal set beand length of the gene head bewhere “” andrepresent the band in the hyperspectral data.From function setF, we know that the maximum number of arguments of all operators is two.According to Equation (1), the length of the gene tail is five.The randomly generated chromosome is shown in Fig.1.

The chromosome shown in Fig.1 consists of two genes.The corresponding ETs are shown in Fig.2.

4.3 Description of RELNC-HGEP

To better describe RELNC-HGEP, the related concepts are given before the RELNC-HGEP algorithm is introduced.

Definition 8.Letbe the optimal fitness value of the estimation function of LNC based on hybrid GEP andbe the maximum fitness value; then,is called the function mining success ratio on estimation of LNC (FMSR-ELNC).

Definition 9.In RELNC-HGEP, fitness functionof theith individual is expressed by equation (2):

Meanwhile, the genetic operation of model mining based on the hybrid GEP includes selection based on elitism, mutation, IS/RIS/Gene transposition, one-point/two-point/gene recombination, etc.

The process of RELNC-HGEP is as Algorithm 3 on next page.

V.SIMULATIONS

In this section, we present some numerical results to evaluate the performance of Algorithms 1 and 2.

5.1 Experiment setup and data source

To test the performance and effectiveness of the proposed algorithm in this paper, simulation experiments are done in a laboratory environment.All experiments are given on the following platform: Intel i5 2.3 GHz+2 G+Win7(64 bit) +Jdk1.7, etc.

The experimental data is mainly from OPTICLEAF, a database of leaf optical properties[52].These experimental data mainly come from the LOPEX93 dataset.Because this dataset contains more plant species, all plant species are divided into three datasets: crops, low fruit trees/shrub/vines (LSV) and arbor.The range of the hyperspectral band is 400-2500 nm.The sample numbers of three datasets are 66, 40, and 105, respectively.For these three datasets, each testing dataset is composed of 20 samples and the remaining samples are treated as three training datasets, respectively.

5.2 Experimental results

5.2.1 LNC and spectral reflectance of plant

The descriptive statistics of leaf nitrogen content (LNC) of crops, LSV and arbor datasets are shown in Table 1.The maximum value is almost three or four times the minimum value for eachLNC.The average raw reflectance spectra of leaves of various plants had similar patterns (Figure 3).Due to the chlorophyll influence, a reflection peak occurs at approximately 550 nm.Meanwhile, a sharp rise(called a red edge) appears between 700 and 750 nm.The reflectance in the near-infrared range (760–1300 nm) is higher than those in other ranges caused by the internal cellular structure of plants.Two absorption peaks occur at approximately 1450 and 1950 nm due to the absorption of water content.

5.2.2 Reduction of hyperspectral band

For crops, LSV and arbor datasets, change of the number of hyperspectral band based on DRND-DD is shown in Table 2.The optimal dimensionality reductions based on DRNDDD, principal component analysis (PCA),singular value decomposition (SVD), the dimensionality reduction algorithm based on a positive region (AR-PR) and the dimensionality reduction algorithm based on a discernable matrix (AR-DM) are shown in Fig.4.

It is well known that the optimal dimensionality reduction is not unique for invariant hyperspectral band according to the Rough Set.From Table 2, we know that DRND-DD is effective for solving an optimal dimension-ality reduction.After reduction, for these three datasets, the numbers of hyperspectral band decreased by 99.52%, 99.52% and 99.48%,respectively.Thus, by means of dimensionality reduction of hyperspectral data, many bands are reduced.These will greatly reduce the complexity of model establishment when using GEP.Meanwhile, according to rough set theory, the reduction of hyperspectral band does not change the decision ability of hyperspectral data.

Algorithm 2: RELNC-HGEP

Table I Descriptive statistics of the leaf nitrogen content (LNC) of crops, LSV and arbor datasets

Table II Change of number of hyperspectral band based on DRND-DD

Fig.3 The average raw reflectance spectra of leaves from six types of plants.

Fig.4 Comparison of the numbers of hyperspectral band after optimal reduction based on five dimensionality reduction algorithms

From Fig.4, compared with AR-PR, ARDM, PCA and SVD, the number of hyperspectral band after optimal reduction based on DRND-DD maximally decreases by 41.18%,41.18% and 38.89% for crops, LSV and arbor datasets, respectively.Furthermore, the optimal dimensionality reduction based on DRND-DD, AR-PR and AR-DM does not result in loss of the original decision information.Meanwhile, dimensionality reduction based on PCA and SVD will inevitably result in partial loss of the original decision information.

In this study, the training dataset was run 10 times using the GEP algorithm and stopped when no significant change was noticed based on the fitness value.For the dataset of crops,the maximum of fitness is 4600 (46 samples)and the fitness values range from 4560.3 to 4564.5 for 10 models.For the dataset of LSV,maximum of fitness is 2000 (20 samples) and the fitness values range from 1992.9 to 1994.3 for 10 models.For the dataset of arbor, maximum of fitness is 8500 (85 samples) and the fitness values range from 8460.5 to 8466.2 for 10 models.

For these three datasets, the numbers of hyperspectral band after optimal reduction are 10, 10 and 11, respectively (Table 3-5).However, for dried plants, the sorption feature in the SWIR region is observed as nitrogen concentration increases, while for fresh leaves,the sorption feature in this region is also observed as water in the leaves increases.So, the models that contain the bands in SWIR region were ignored.

For the dataset of crops, the wavelengths are located in the blue and green region (ranging from 400-550 nm), red region (ranging from 670-698 nm) and near-infrared region(Table 3).For the LSV dataset, the wavelengths are located in the blue and green region (also ranging from 400-550 nm), rededge, and near-infrared regions (ranging from 700-900 nm) (Table 4).For the arbor dataset,the wavelengths are located in the blue, green,and near-infrared regions (Table 5).These results are consistent with the findings of some studies on LNC estimation [15, 18, 53].

The hyperspectral band at 423 nm was one of the selected spectra used by Wang for LNC estimation [15].Schlemmer et al.found that the nitrogen contents in maize at the leaf and canopy levels can be accurately retrieved at the green band (approximately 550 nm) [53].Abdel-Rahman [46] indicated that the red edge (670-780 nm) is in the vegetation spectra between low reflectance in the red region and high reflectance in the near-infrared, which is associated with chlorophyll content and consequently to nitrogen.Fitzgerald et al.[54]indicated that the canopy chlorophyll content index can be designed to detect canopy nitrogen using three wavebands in the red-edge region.Moreover, some authors have reported that the red-edge and near-infrared regions are good indicators for nitrogen estimation in plants [14, 16, 55].

5.2.3 Time-consumption for different algorithms

Fig.5 shows that time-consumption for solving the optimal reduction based on DRNDDD, AR-PR, and AR-DM is less than that based on PCA and SVD.However, in comparison with AR-PR and AR-DM forcrops, LSVandarbordatasets, the time-consumption of DRND-DD reduces to approximately 27.49%and 26.96%, 26.38% and 22.71%, 16.87% and 14.69%, respectively.This is mainly because the maximum time complexity of DRND-DD iswhile the time complexity of ARPR, AR-DM, PCA, and SVD is approximately, andrespectively.Here,represents the number of instances in the hyperspectral data andrepresents the number of hyperspectral band.

5.2.4 LNC estimation

After dimensionality reduction, for LNC estimation, the performance of RELNC-HGEP is described in the following experiment.Parameters of GEP are shown in Table 6.Table 7 shows a comparison of optimal and maximum

fitness values by using RELNC-HGEP before

and after reduction.Fig.6 shows a compar-ison of the function mining success ratio of RELNC-HGEP before and after dimensionality reduction.Under the condition that RELNC-HGEP runs 5 times, comparison of average time-consumption before and after reduction is shown in Fig.7.Fig.8 and Fig.9 show,respectively, comparison between the real value and model value and correlation between the real value and estimation value of the leaf nitrogen content for training and test datasets by using RELNC-HGEP.Meanwhile, performance comparison of RELNC-HGEP, partial least squares regression (PLSR) [17] and support vector machine regression (SVMR) [17]are described in Table 8

Table III Statistical performance of each model (For crops)

Table IV Statistical performance of each model (For LSV)

Table V Statistical performance of each GEP model (For arbor)

Table VI Parameters of GEP

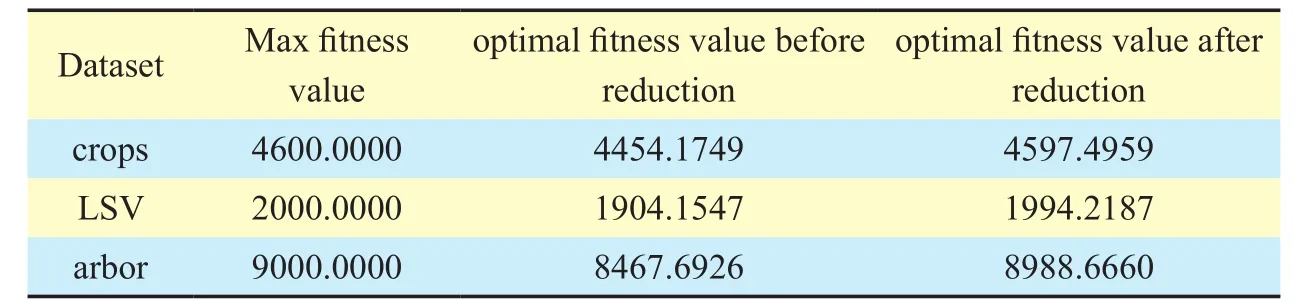
Table VII Comparison of optimal and maximum fitness value before and after dimensionality reduction

From Table 7, for crops, LSV and arbor datasets, we know that in comparison with the difference between the optimal and maximum fitness value before the dimensionality reduction, the difference after the dimensionality reduction has decreased by approximately 98.28%, 93.97% and 97.87%, respectively.According to Definition 7, we get the function mining success ratio ofcrops, LSV and arbor datasets, respectively.From Fig.6, forcrops,LSVandarbor, the function mining success ratio has been improved by approximately 3.12%, 4.5% and 5.79%, respectively.This means that for high-dimensional hyperspectral data, dimensionality reduction greatly improves the success probability of function mining without changing the decision capability of the existing hyperspectral dataset.Fig.7 shows that dimensionality reduction greatly reduces the average time-consumption of the reflectance estimation model between LNC and hyperspectral band by using RELNC-HGEP for the same hyperspectral dataset.Forcrops,LSV and arbordatasets, the average time-consumption has been maximally dropped by approximately 57.52%, 40.44% and 71.38%,respectively, under the same parameters.This is mainly because the dimensionality reduction can drastically decrease redundant hyperspectral band so that the analysis of hyperspectral data by using GEP is greatly simplified.

From Fig.8 (a), (c) and (e), for these three trainingdatasets, we can see that the maximum error between the real value and model value of the leaf nitrogen content is 0.59, 0.14 and 0.34, respectively, and that the minimum error is 0.01, 0.02 and 0.01, respectively.From Fig.8 (b), (d) and (f), for these three training datasets, the determinant coefficient between the real value and estimation value of the leaf nitrogen content is 0.9707, 0.98 and 0.9704,respectively.For these three testdatasets, Fig.9 (a), (c) and (e) indicate that the maximum error between the real value and model value of the leaf nitrogen content is 1.52, 0.9 and 0.83, respectively, while the minimum error is 0.09, 0.1 and 0.05, respectively.For these three testdatasets, from Fig.9 (b), (d) and(f), we know that the determinant coefficient between the real value and estimation value of the leaf nitrogen content is 0.7119, 0.6233 and 0.7448, respectively.It can be seen that the model between LNC and hyperspectral band based on RELNC-HGEP has high estimation accuracy.

VI.CONCLUSIONS

Fig.6 Comparison of function mining success ratio of RELNC-HGEP before and after dimensionality reduction

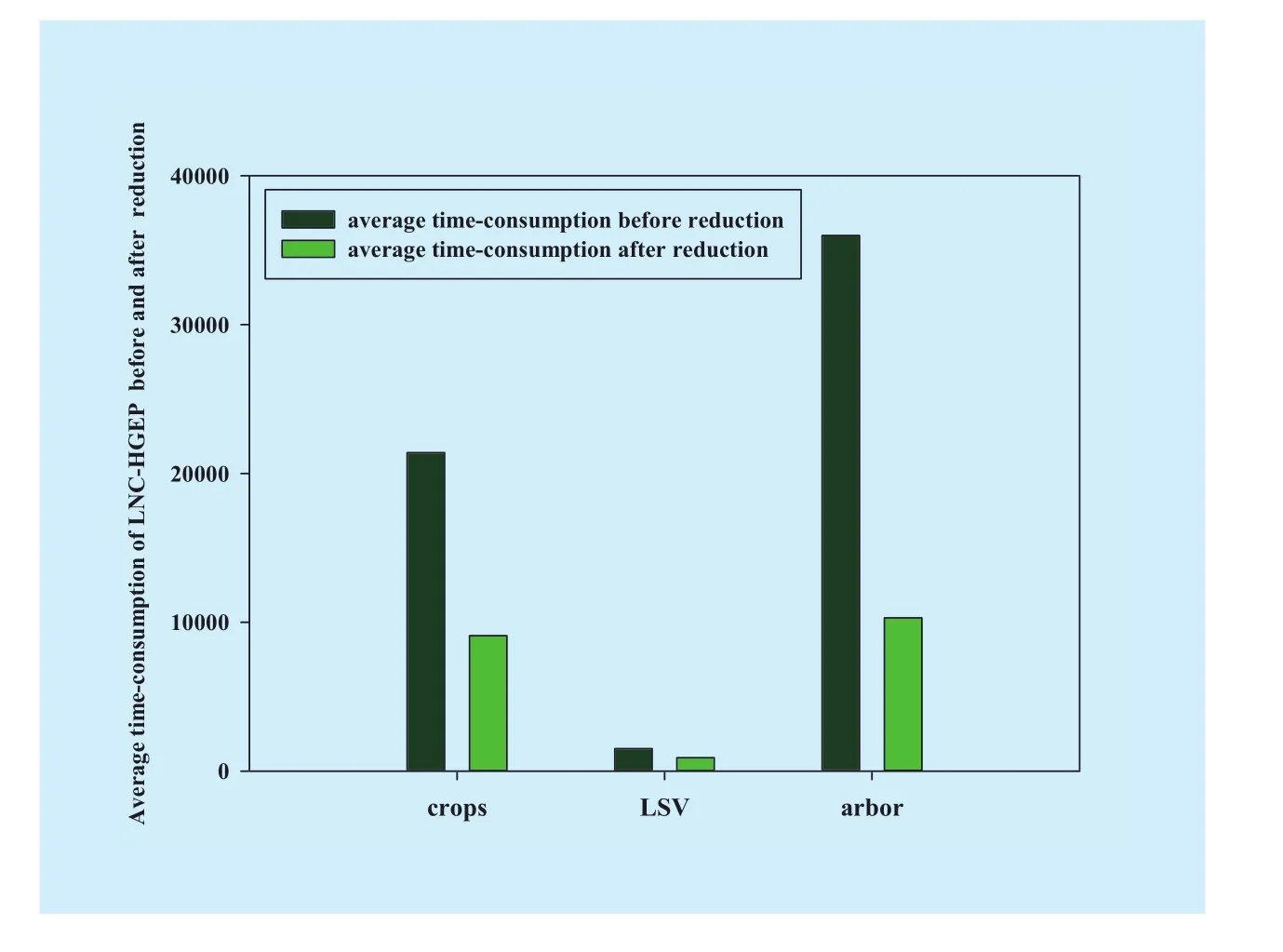
Fig.7 Comparison of average time-consumption before and after dimensionality reduction

This paper has proposed a reflectance estimation model between leaf nitrogen content and hyperspectral band for monitoring plant growth via hybrid gene expression programming (REMLNC-HGEP).REMLNC-HGEP overcomes the defect, i.e., that the traditional regression methods need to rely on prior knowledge.The major results of this paper are as follows.

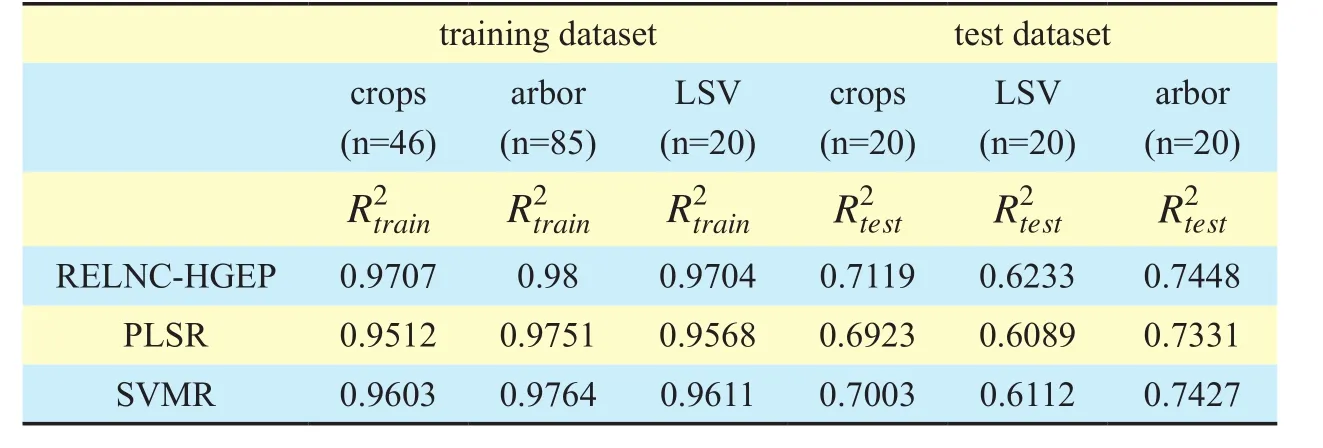
Table VIII Comparison of determinant coefficient between the real value and estimation value of the leaf nitrogen content based on RELNC-HGEP, PLSR and SVMR

The gene expression programming algorithm, an evolutionary algorithm, was applied to develop a new reflectance estimation model between leaf nitrogen content and hyperspectral band.Before reflectance estimation model evaluation, the dimensionality reduction algorithm with noise data based on dependence degree (DRND-DD) is used to reduce the hyperspectral data’s complexity.The experimental results showed that REMLNC-HGEP had great potential for mining the reflectance estimation model between leaf nitrogen content and the hyperspectral band of plants.The method can not only improve the prediction accuracy of the reflectance estimation model of leaf nitrogen content but also reduce the difficulty of hyperspectral data processing.The proposed model and existing reflectance estimation model of leaf nitrogen content were both tested in terms of their model mining success ratio, average time-consumption and coefficient of correlation (R2).The results indicated that the reflectance estimation model based on REMLNC-HGEP has advantages in model mining success ratio, average time-consumption and coefficient of correlation.Specifically, for the crops, LSV and arborhyperspectral datasets, regarding the mining success ratio, the function mining success ratio based on REMLNC-HGEP before and after DRNDDD improved by approximately 3.12%, 4.5%and 5.79%, respectively; regarding average time-consumption, average time-consumption based on REMLNC-HGEP before and after DRND-DD maximally dropped by approximately 57.52%, 40.44% and 71.38%, respectively; regarding the coefficient of correlation,compared with partial least squares regression(PLSR) and support vector machine regression(SVMR), the R2of REMLNC-HGEP improved by 1%.These results indicate that the REMLNC-HGEP model has a high mining success ratio, low average time-consumption and high predictive accuracy.This will provide a good foundation for timely and accurate assessment and prediction of plant growth in the future.

With the development of remote sensing,more and more hyperspectral data will be collected and stored.The proposed algorithm in this paper will be difficult to deal with these massive hyperspectral sensor data in single computer.How to deal with massive data is an important direction of development in the future [56-61].Distributed computing technology based on cloud computing will be a good choice.Meanwhile, Security, is also an important issue that must be considered in dealing with these massive data in the future[62-68].

ACKNOWLEDGMENT

This work was supported in part by the National Natural Science Foundation of China(11&zd167, 51507084, 61572262), NSF of Jiangsu Province (BK20141427), NUPT(NY214097), Open research fund of Key Lab of Broadband Wireless Communication and Sensor Network Technology (NUPT), Ministry of Education (NYKL201507), Qinlan Project of Jiangsu Province and the General Project of National Natural Science Found of China under Grant 41471300.

[1] Q.Wang, S.Leng, H.Fu, Y.Zhang, and H.Weerasinghe,An Enhanced Multi-Channel MAC for the IEEE 1609.4 Based Vehicular Ad Hoc Networks: IEEE, 2010.

[2] L.Zhang and Y.Zhang, “Energy-Efficient Cross-Layer Protocol of Channel-Aware Geographic-Informed Forwarding in Wireless Sensor Networks,”IEEE Transactions on Vehicular Technology,vol.58, pp.3041-3052, 2009.

[3] X.Zhang, Z.Yi, Z.Yan, G.Min, W.Wang, A.Elmokashfi, et al., “Social Computing for Mobile Big Data,” vol.49, pp.86-90, 2016.

[4] Y.Zhang, R.Yu, M.Nekovee, Y.Liu, S.Xie, and S.Gjessing, “Cognitive machine-to-machine communications: visions and potentials for the smart grid,”IEEE Network,vol.26, pp.6-13,2012.

[5] Y.Zhang, R.Yu, S.Xie, W.Yao, Y.Xiao, and M.Guizani, “Home M2M networks: Architectures,standards, and QoS improvement,”IEEE Communications Magazine,vol.49, pp.44-52, 2011.

[6] S.Xie and Y.Wang, “Construction of Tree Network with Limited Delivery Latency in Homogeneous Wireless Sensor Networks,”Wireless Personal Communications,vol.78, pp.231-246,2014.

Fig.9 Comparison between the real value and model value of the leaf nitrogen content for (a) crops, (c) LSV and (e) arbor test datasets and determinant coeffi-cient between the real value and estimation value of the leaf nitrogen content for(b) crops, (d) LSV and (f) arbor test datasets in the RELNC-HGEP

[7] K.Wang, Z.Ouyang, R.Krishnan, and L.Shu, “A Game Theory-Based Energy Management System Using Price Elasticity for Smart Grids,”IEEE Transactions on Industrial Informatics,vol.11,pp.1607-161, 2015.

[8] Y.Zheng, J.Byeungwoo, D.Xu, Q.M.J.Wu, and Z.Hui, “Image segmentation by generalized hierarchical fuzzy C-means algorithm,”Journal of Intelligent & Fuzzy Systems,vol.28, pp.4024-4028, 2015.

[9] B.Gu, X.Sun, and V.S.Sheng, “Structural Minimax Probability Machine,”IEEE Transactions on Neural Networks & Learning Systems,pp.1-11,2016.

[10] K.Wang, Y.Wang, Y.Sun, S.Guo, and J.Wu,“Green industrial Internet of Things architecture:an energy-effi cient perspective,”IEEE Communications Magazine,vol.54, pp.1-7, 2016.

[11] S.Jun, L.Bing, and W.Xiaohong, “The prediction of rice leaf’s nitrogen content based on leaf spectrum on the heading stage,” inControl Conference (CCC), 2010 29th Chinese, 2010, pp.2704-2707.

[12] X.Yao, Y.Zhu, Y.Tian, W.Feng, and W.Cao, “Exploring hyperspectral bands and estimation indices for leaf nitrogen accumulation in wheat,”International Journal of Applied Earth Observation and Geoinformation,vol.12, pp.89-100,2010.

[13] Y.Tian, X.Yao, J.Yang, W.Cao, D.Hannaway,and Y.Zhu, “Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground-and space-based hyperspectral reflectance,”Field Crops Research,vol.120, pp.299-310, 2011.

[14] Y.Inoue, E.Sakaiya, Y.Zhu, and W.Takahashi,“Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements,”Remote Sensing of Environment,vol.126, pp.210-221, 2012.

[15] W.Wang, X.Yao, X.Yao, Y.Tian, X.Liu, J.Ni,et al., “Estimating leaf nitrogen concentration with three-band vegetation indices in rice and wheat,”Field Crops Research,vol.129, pp.90-98, 2012.

[16] C.Zhao, Z.Wang, J.Wang, and W.Huang, “Relationships of leaf nitrogen concentration and canopy nitrogen density with spectral features parameters and narrow-band spectral indices calculated from field winter wheat (Triticum aestivum L.) spectra,”International journal of remote sensing,vol.33, pp.3472-3491, 2012.

[17] Y.Zhai, L.Cui, X.Zhou, Y.Gao, T.Fei, and W.Gao, “Estimation of nitrogen, phosphorus, and potassium contents in the leaves of different plants using laboratory-based visible and near-infrared reflectance spectroscopy: comparison of partial least-square regression and support vector machine regression methods,”International journal of remote sensing,vol.34,pp.2502-2518, 2013.

[18] W.Feng, B.-B.Guo, Z.-J.Wang, L.He, X.Song,Y.-H.Wang, et al., “Measuring leaf nitrogen concentration in winter wheat using double-peak spectral reflection remote sensing data,”Field Crops Research,vol.159, pp.43-52, 2014.

[19] B.Gu, V.S.Sheng, Z.Wang, D.Ho, S.Osman,and S.Li, “Incremental learning for ν -Support Vector Regression,”Neural Networks the Official Journal of the International Neural Network Society,vol.67, pp.140-150, 2015.

[20] B.Gu, V.S.Sheng, K.Y.Tay, W.Romano, and S.Li, “Incremental Support Vector Learning for Ordinal Regression,”IEEE Transactions on Neural Networks & Learning Systems,vol.26, pp.1403-1416, 2014.

[21] L.Du, W.Gong, S.Shi, J.Yang, J.Sun, B.Zhu, et al., “Estimation of rice leaf nitrogen contents based on hyperspectral LIDAR,”International Journal of Applied Earth Observation and Geoinformation,vol.44, pp.136-143, 2016.

[22] M.Kalacska, M.Lalonde, and T.Moore, “Estimation of foliar chlorophyll and nitrogen content in an ombrotrophic bog from hyperspectral data: Scaling from leaf to image,”Remote Sensing of Environment,vol.169, pp.270-279, 2015.

[

23] S.Sumriddetchkajorn and Y.Intaravanne, “Single-wavelength based rice leaf color analyzer for nitrogen status estimation,”Optics and Lasers in Engineering,vol.53, pp.179-184, 2014.

[24] J.R.Koza,Genetic programming: on the programming of computers by means of natural selectionvol.1: MIT press, 1992.

[25] C.Ferreira, “Genetic representation and genetic neutrality in gene expression programming,”Advances in Complex Systems,vol.5, pp.389-408, 2002.

[26] C.Ferreira,Gene expression programming:mathematical modeling by an artificial intelligencevol.21: Springer, 2006.

[27] M.Z.Hashmi, A.Y.Shamseldin, and B.W.Melville, “Statistical downscaling of watershed precipitation using Gene Expression Programming(GEP),”Environmental Modelling & Software,vol.26, pp.1639-1646, 2011.

[28] H.Wang, S.Liu, F.Meng, and M.Li, “Gene expression programming algorithms for optimization of water distribution networks,”Procedia Engineering,vol.37, pp.359-364, 2012.

[29] J.Shiri and Ö.Kişi, “Application of artificial intelligence to estimate daily pan evaporation using available and estimated climatic data in the Khozestan Province (South Western Iran),”Journal of irrigation and drainage engineering,vol.137, pp.412-425, 2011.

[30] G.Landeras, J.J.López, O.Kisi, and J.Shiri,“Comparison of Gene Expression Programming with neuro-fuzzy and neural network computing techniques in estimating daily incoming solar radiation in the Basque Country (Northern Spain),”Energy Conversion and Management,vol.62, pp.1-13, 2012.

[31] H.M.Azamathulla, “Gene-expression programming to predict friction factor for Southern Italian rivers,”Neural Computing and Applications,vol.23, pp.1421-1426, 2013.

[32] Ö.Terzi, “Daily pan evaporation estimation using gene expression programming and adaptive neural-based fuzzy inference system,”Neural Computing and Applications,vol.23, pp.1035-1044, 2013.

[33] S.Traore and A.Guven, “New algebraic formulations of evapotranspiration extracted from gene-expression programming in the tropical seasonally dry regions of West Africa,”Irrigation Science,vol.31, pp.1-10, 2013.

[34] M.A.Yassin, A.Alazba, and M.A.Mattar, “A new predictive model for furrow irrigation infiltration using gene expression programming,”Computers and Electronics in Agriculture,vol.122, pp.168-175, 2016.

[35] C.R.Zorn and A.Y.Shamseldin, “Peak flood es-timation using gene expression programming,”Journal of Hydrology,vol.531, pp.1122-1128,2015.

[36] M.A.Yassin, A.Alazba, and M.A.Mattar, “Artificial neural networks versus gene expression programming for estimating reference evapotranspiration in arid climate,”Agricultural Water Management,vol.163, pp.110-124, 2016.

[37] P.Dey and A.K.Das, “A utilization of GEP (gene expression programming) metamodel and PSO(particle swarm optimization) tool to predict and optimize the forced convection around a cylinder,”Energy,vol.95, pp.447-458, 2016.

[38] I.B.Strachan, E.Pattey, and J.B.Boisvert, “Impact of nitrogen and environmental conditions on corn as detected by hyperspectral reflectance,”Remote Sensing of Environment,vol.80, pp.213-224, 2002.

[39] S.S.Shen, “Optimal band selection and utility evaluation for spectral systems,”Hyperspectral Data Exploitation: Theory and Applications,pp.227-43, 2007.

[40] P.S.Thenkabail, E.A.Enclona, M.S.Ashton, C.Legg, and M.J.De Dieu, “Hyperion, IKONOS,ALI, and ETM+ sensors in the study of African rainforests,”Remote Sensing of Environment,vol.90, pp.23-43, 2004.

[41] B.L.Becker, D.P.Lusch, and J.Qi, “Identifying optimal spectral bands from in situ measurements of Great Lakes coastal wetlands using second-derivative analysis,”Remote Sensing of Environment,vol.97, pp.238-248, 2005.

[42] M.Pal, “Random forest classifier for remote sensing classification,”International Journal of Remote Sensing,vol.26, pp.217-222, 2005.

[43] G.BAO, Z.-h.QIN, Y.ZHOU, Y.-h.BAO, X.-p.XIN,Y.HONG, et al., “The Application of Hyper-spectral Data and RBF Neural Network Method to Retrieval of Leaf Area Index of Grassland,”Remote Sensing for Land & Resources,vol.2, p.003, 2012.

[44] K.-S.Lee, W.B.Cohen, R.E.Kennedy, T.K.Maiersperger, and S.T.Gower, “Hyperspectral versus multispectral data for estimating leaf area index in four different biomes,”Remote Sensing of Environment,vol.91, pp.508-520,2004.

[45] Z.Pawlak, “Rough sets,”International Journal of Computer & Information Sciences,vol.11, pp.341-356, 1982.

[46] E.M.Abdel-Rahman, F.B.Ahmed, and R.Ismail,“Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data,”International Journal of Remote Sensing,vol.34, pp.712-728, 2013.

[47] Y.Grossman, S.Ustin, S.Jacquemoud, E.Sanderson, G.Schmuck, and J.Verdebout, “Critique of stepwise multiple linear regression for the extraction of leaf biochemistry information from leaf reflectance data,”Remote Sensing of Environment,vol.56, pp.182-193, 1996.

[48] X.-y.LI, G.-s.LIU, Y.-f.YANG, C.-h.ZHAO, Q.-w.YU, and S.-x.SONG, “Relationship between hyperspectral parameters and physiological and biochemical indexes of flue-cured tobacco leaves,”Agricultural Sciences in China,vol.6, pp.665-672, 2007.

[49] P.Geladi and B.R.Kowalski, “Partial leastsquares regression: a tutorial,”Analytica chimica acta,vol.185, pp.1-17, 1986.

[50] C.Ferreira, “Gene Expression Programming: A New Adaptive Algorithm for Solving Problems,”Complex Systems,vol.13, pp.87-129, 2001.

[51] S.Wolfram,The mathematica bookvol.35,2000.

[52]Leaf Optical Properties Experiment 93 (LOPEX93).Available: http://teledetection.ipgp.jussieu.fr/opticleaf/lopex.htm (accessed on 22 September 2015)

[53] M.Schlemmer, A.Gitelson, J.Schepers, R.Ferguson, Y.Peng, J.Shanahan, et al., “Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels,”International Journal of Applied Earth Observation and Geoinformation,vol.25, pp.47-54, 2013.

[54] G.Fitzgerald, D.Rodriguez, and G.O’Leary,“Measuring and predicting canopy nitrogen nutrition in wheat using a spectral index—The canopy chlorophyll content index (CCCI),”Field Crops Research,vol.116, pp.318-324, 2010.

[55] K.Yu, F.Li, M.L.Gnyp, Y.Miao, G.Bareth, and X.Chen, “Remotely detecting canopy nitrogen concentration and uptake of paddy rice in the Northeast China Plain,”ISPRS Journal of Photogrammetry and Remote Sensing,vol.78, pp.102-115, 2013.

[56] K.Wang, Y.Shao, L.Shu, and C.Zhu, “Mobile big data fault-tolerant processing for ehealth networks,”IEEE Network,vol.30, pp.36-42,2016.

[57] K.Wang, J.Mi, C.Xu, Q.Zhu, L.Shu, and D.J.Deng, “Real-Time Load Reduction in Multimedia Big Data for Mobile Internet,”Acm Transactions on Multimedia Computing Communications &Applications,vol.12, 2016.

[58] K.Wang, Y.Shao, L.Shu, and G.Han, “LDPA: a local data processing architecture in ambient assisted living communications,”Communications Magazine IEEE,vol.53, pp.56-63, 2015.

[59] H.Jiang, K.Wang, Y.Wang, and M.Gao, “Energy Big Data: A Survey,”IEEE Access,vol.4, pp.3844-3861, 2016.

[60] X.Wen, L.Shao, Y.Xue, and W.Fang, “A rapid learning algorithm for vehicle classification,”Information Sciences,vol.295, pp.395-406, 2015.

[61] B.Gu and V.S.Sheng, “A Robust Regularization Path Algorithm for ν-Support Vector Classification,”IEEE Transactions on Neural Networks &Learning Systems,vol.1, pp.1-8, 2016.

[62] K.Wang, X.Qi, L.Shu, D.-j.Deng, and J.J.P.C.Rodrigues, “Towards trustworthy crowdsourcing in the social internet of things,” vol.23, pp.30-36, 2016.

[63] K.Wang, M.Du, D.Yang, C.Zhu, J.Shen, and Y.Zhang, “Game-Theory-Based Active Defense for Intrusion Detection in Cyber-Physical Embedded Systems,”Acm Transactions on Embedded Computing Systems,vol.16, 2016.

[64] K.Wang, H.Gao, X.Xu, and J.Jiang, “An Energy-efficient Reliable Data Transmission Scheme for Complex Environmental Monitoring in Underwater Acoustic Sensor Networks,”IEEE Sensors Journal,vol.16, pp.4051-4062, 2015.

[65] J.Shen, H.Tan, S.Moh, and I.Chung, “Enhanced secure sensor association and key management in wireless body area networks,”Journal of Communications & Networks,vol.17, pp.453-462, 2015.

[66] K.Wang, H.Lu, L.Shu, and J.J.Rodrigues, “A context-aware system architecture for leak point detection in the large-scale petrochemical industry,”IEEE Communications Magazine,vol.52, pp.62-69, 2014.

[67] Z.Xia, X.Wang, X.Sun, Q.Liu, and N.Xiong,“Steganalysis of LSB matching using differences between nonadjacent pixels,”Multimedia Tools and Applications,vol.75, pp.1-16, 2016.

[68] K.Wang, M.Du, Y.Sun, A.Vinel, and Y.Zhang,“Attack detection and distributed forensics in machine-to-machine networks,”IEEE Network,vol.30, pp.49-55, 2016.

Biographies

Song Deng,is an associate professor at the Institute of Advanced Technology, Nanjing University Post &Telecommunication.He received his Ph.D.degree in Information Network from the Nanjing University Post & Telecommunication in 2009.His research interests include intelligent control theory and its application, nonlinear system analysis and optimization,and pattern recognition.