硝基胍溶液的热分解性能及动力学
2017-05-08陈莹莹陈利平陈网桦薛倍倍
陈莹莹, 陈利平, 陈网桦, 董 泽,2, 薛倍倍, 张 军, 王 炎
(1. 南京理工大学化工学院安全工程系, 江苏 南京 210094; 2. 索尔维投资有限公司, 上海 200000)
1 引 言
硝基胍(NQ)[1-4]广泛应用于火炸药制造中,是发射剂、推进剂和炸药的重要组分,也可作为机动车辆或飞行器安全气囊的产气剂组分[5]。同时硝基胍具有一定燃爆危险性和毒性,受热、明火、摩擦、震动、撞击时可发生爆炸,其高热下的分解将产生有毒的氮氧化物[6]。我国危险化学品名录将硝基胍分为第一类(爆炸品),第一项(具有整体爆炸危险的物质和物品)。硝基胍的制备属于间接硝化,被列入重点监管危险化工工艺目录。
国内外学者针对其热分解特性展开了一系列研究。刘子如[7]及Lee P P等[8]分别利用差示扫描量热仪(DSC)和绝热量热仪(ARC)得到了硝基胍在动态模式下和绝热模式下基本的热分解参数。Lee P P和Back M H[9]证实了DSC实验样品池是否密闭、气氛的不同都会对硝基胍热流曲线具有一定影响。李艳春等[10]提出硝基胍具有复杂的分解机理,并得到其分解由三步连续反应组成。洪三国、傅孝愿[11]用量子化学方法研究了硝基胍热解反应的机理,提出硝基胍热解反应可经历两条相互竞争的途径,并认为其分解主产物为N2O、H2O和NH3。刘子如等[12]也得到硝基胍的分解会产生大量N2O、H2O及NH3、H2N—NH2。Volk F[13]则检测到硝基胍的分解过程存在一种具有较高热安定性的中间产物嘧勒胺。
由于硝基胍的危险性,联合国危险物品运输专家委员会[14]建议其可加水后进行储存和运输。但目前尚缺乏以硝基胍水溶液为研究对象的工作,因此探究硝基胍水溶液的热分解行为,具有实用价值。
另一方面,是否具有自催化性质是研究物质分解特性的一个重要方向。自催化性质指的是物质在分解过程中的产物对其自身的反应具有催化加速的作用[15]。等温DSC实验通常被作为鉴别物质是否具有自催化性质的一种有效手段。具有自催化性质的物质,在等温条件下,其反应速率不会随着反应进程呈单调递减趋势。而是经过一定时间的诱导期后,放热速率随反应进程而增加,到达最大值后才下降,表现出一个钟型的放热峰。由于具有此种性质的物质在诱导期内的反应十分缓慢,难以觉察,容易被人们忽略; 但反应一旦被引发,便在较短时间内快速发生,且往往具有较大的温度和压力效应,需要引起重视。
本研究利用动态和等温DSC研究硝基胍水溶液的热分解特性,采用无模型方法(Friedman方法)对两种模式数据进行活化能求解,并利用活化能的求解结果作为物质反应机理是否单一的判据。由于等温DSC实验表明其分解反应具有自催化性质,进一步采用一种将引发反应考虑在内的自催化模型,利用模型拟合法计算硝基胍水溶液的分解反应动力学参数并进行验证。
2 实验部分
2.1 试剂与仪器
仪器: 热通量型差示扫描量热仪(DSC-1),瑞士METTLER TOLEDO公司生产。样品池均为带镀金垫片的不锈钢高压坩埚,耐压15 MPa。
试剂: 硝基胍,工业纯,辽宁庆阳化学工业公司。
2.2 实验条件
将一定量的硝基胍置于DSC坩埚中,滴加一定量的沸水,使两者在高温下互溶[6],设置动态DSC实验升温速率为1,2,4,8 ℃·min-1,等温DSC实验温度分别为112,114,120,124 ℃; 动态及等温DSC试验所用样品量分别见表1和表2,由于加样困难,未能做到被测试样高温下的浓度完全一致,但保持硝基胍质量浓度在29.45%~29.77%。两种模式下的实验,均采用空坩埚做参比,氮气气氛,流速为50 ℃·min-1。
表1 动态DSC实验样品量
Table 1 Sample mass used in dynamic DSC experiments
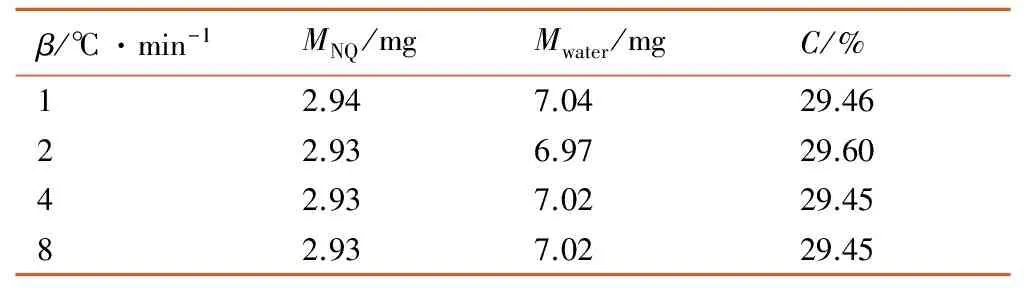
β/℃·min-1MNQ/mgMwater/mgC/%12.947.0429.4622.936.9729.6042.937.0229.4582.937.0229.45
Note:βis the heating rate,MNQis the mass of NQ,Mwateris the mass of water,Cis the mass percent of NQ.
表2 等温DSC实验样品量
Table 2 Sample mass used in isothermal DSC experiments

isothermaltemperature/℃MNQ/mgMwater/mgC/%1122.956.9629.761142.956.9429.771202.957.0029.651242.936.9629.63
3 结果与讨论
3.1 硝基胍溶液动态DSC热分解特性
硝基胍溶液的动态DSC测试曲线见图1。由图1可知,硝基胍溶液的动态DSC曲线存在一个分解放热峰,起始分解温度较高(Tonset=149~185 ℃)。从图1可以看出随着升温速率增加,放热峰向高温区移动,起始分解温度Tonset和峰温Tp升高,最大放热速率增加。四次试验的平均比放热量约为311 J·g-1。
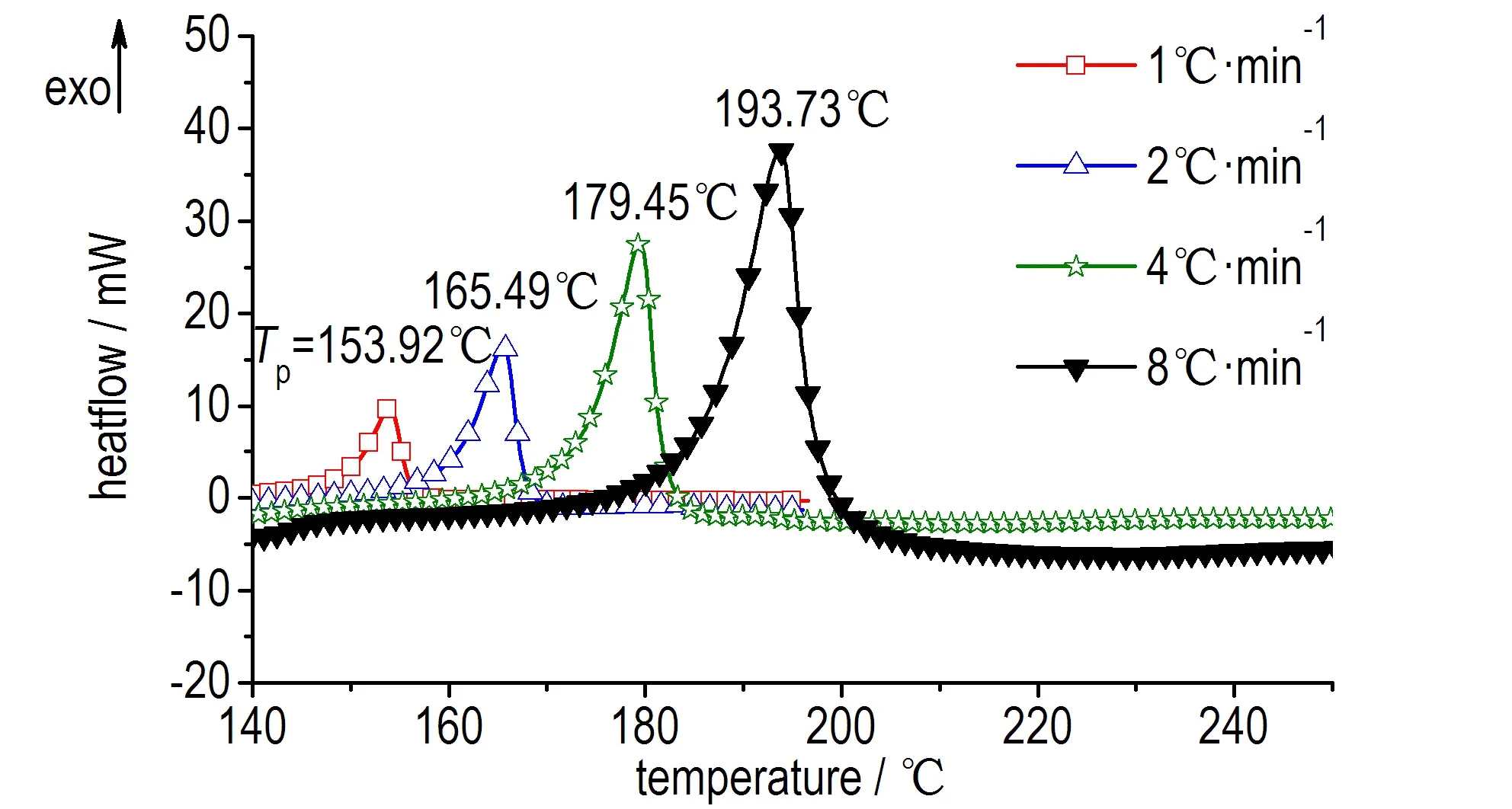
图1 硝基胍溶液动态DSC测试曲线
Fig.1 Dynamic DSC curves of NQ solution
3.2 硝基胍溶液等温DSC热分解特性
在动态DSC实验的基础上,进行了等温DSC实验(等温实验温度分别为112,114,120,124 ℃),如图2所示。结果显示硝基胍溶液的等温分解放热速率表现为钟型曲线,放热速率达到最大值后开始下降,表明硝基胍溶液的分解具有自催化性质(N级机理的物质在等温条件下,其放热速率随时间单调下降)[15]。且随着等温温度的升高,反应程度愈发剧烈,等温诱导期缩短(112 ℃时等温诱导期为255.76 min,114 ℃时等温诱导期为190.28 min,120 ℃时等温诱导期为116.45 min,124 ℃时等温诱导期为75.48 min)。等温条件下分解反应平均比放热量为305 J·g-1,与动态DSC结果接近。

图2 硝基胍溶液等温DSC测试曲线
Fig.2 Isothermal DSC curves of NQ solution
3.3 硝基胍溶液动力学参数计算
3.3.1 硝基胍溶液动态DSC活化能
采用等转化率微分方法中的Friedman法,在不涉及模式函数的情况下获取可靠的活化能。式(1)为Friedman方程[16],由此可以得到每一个反应转化率α下的活化能Eα值。
(1)
式中,β为温升速率,℃·min-1;α为转化率;Aα为反应转化率α下的指前因子,s-1;f(α)为机理函数,Eα为活化能,kJ·mol-1;R为理想气体常数,8.314 J·mol-1·K-1;T为温度,K。
根据热分析动力学委员会的建议[16]: Friedman法求得的活化能曲线形状可以作为判断反应是否可用单一速率方程描述的依据。放热开始和即将结束阶段,活化能Eα值受基线影响很大,一般主要关注0.1<α<0.9下的求解结果。图3中动态DSC模式下硝基胍溶液的活化能值在0.1<α<0.9时,活化能变化不大(84~78 kJ·mol-1),表明硝基胍溶液的热分解反应可以用单一的速率方程来描述。
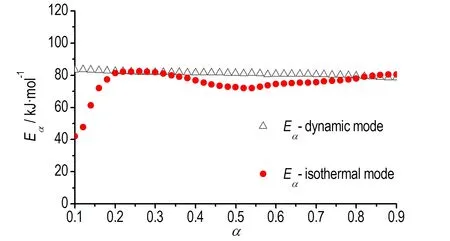
图3 Friedman法计算硝基胍溶液的活化能
Fig.3Eαof NQ solution (Friedman method)
3.3.2 硝基胍溶液等温DSC活化能
对于等温DSC,Friedman法方程见式(2):
(2)
式(2)中(dα/dt)α为反应速率,s-1。其它符号的含义同公式(1)。
求解结果见图3。可见,硝基胍溶液等温模式下活化能在0.1<α<0.2时出现较大变化,但在0.2<α<0.9时,活化能变化较小(86~78 kJ·mol-1),与动态模式下求得的活化能非常接近,同样表明硝基胍溶液分解反应可用单步反应速率方程描述。
3.3.3 硝基胍溶液动力学模型求解
上述研究显示,硝基胍溶液的分解反应属于单步机理,且具有自催化特性,众所周知,S-B模型[17]是一种典型的自催化模型,其计算方法见式(3)。
(3)
式中,m,n为自催化模型的反应级数。
但是S-B模型忽略了自催化反应的引发反应,对于强自催化的情况,这种忽略对动力学求解影响不大。而对于弱自催化的情况,引发反应则不能被忽略。因此采用将引发反应考虑在内的自催化模型[17-20],即假设该自催化反应包含(4)、(5)两个步骤。
A→B (initial stage)
(4)
A+B→2B (autocatalytic stage)
(5)
其中式(4)为引发反应,式(4)为具有自催化性质的分解反应。于是得到反应速率如式(6)所示。该模型已被证实能够更好地描述自催化反应,并被应用于多种含能材料的分解反应动力学参数求解中。
(6)
式中,k1和k2分别为两步反应各自的速率常数;n1、n2为自催化反应的反应级数。
基于上述公式,对4条等温DSC曲线分别进行非线性拟合计算。本研究利用MATLAB软件的lsqnonlin函数实现非线性拟合运算,将转化率和转化率速率分别定义为自变量和应变量,并对k1和k2、n1和n2赋以初值1,可得到每个温度下的k1和k2、n1和n2计算结果见表3。结果表明拟合的相关系数很高,且不同温度下得到的反应级数都很接近,其中n1平均值为1.111,n2平均值为1.995。基于阿仑尼乌斯速率常数表达式(式(7)):
(7)
式中,A为指前因子,s-1;E为活化能,kJ·mol-1。
表3 等温DSC数据的非线性拟合计算结果
Table 3 Nonlinear fitting results based on isothermal DSC data
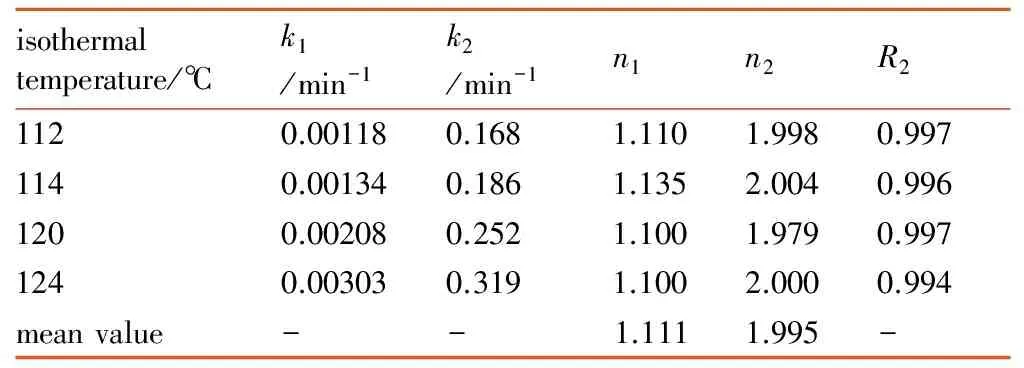
isothermaltemperature/℃k1/min-1k2/min-1n1n2R21120.001180.1681.1101.9980.9971140.001340.1861.1352.0040.9961200.002080.2521.1001.9790.9971240.003030.3191.1002.0000.994meanvalue--1.1111.995-
将lnk1对1/T进行线性拟合(见图4),得到活化能E1和lnA1分别为92.17 kJ·mol-1和18.03 s-1。同理得到E2和lnA2分别为76.40 kJ·mol-1和18.00 s-1,相关数据见表4。线性拟合方法求得的活化能的值与上文Friedman方法的计算结果接近,一定程度上证实了数值的可靠性。
因此,硝基胍溶液的反应速率可以表示为:
(8)
为了验证上述模型,采用获得的反应速率表达式对动态DSC的测试结果进行计算和比较,结果如图5所示。图5显示基于上述反应速率方程所得到的计算结果与动态DSC(1,2,4,8 ℃·min-1)实验的结果十分吻合,证实了所得模型可以很好地描述硝基胍溶液的热分解。
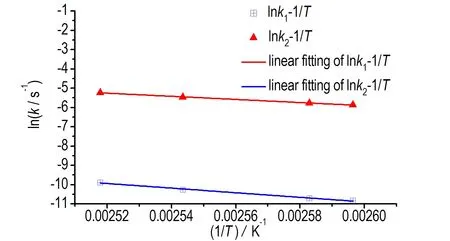
图4 lnk-1/T曲线(计算E1、E2和lnA1、lnA2)
Fig.4 lnk-1/Tcurves (caculatedE1,E2and lnA1, lnA2)
表4 线性拟合(lnk1, 1/T)、(lnk2, 1/T)的计算结果
Table 4 Linear fitting results of (lnk1, 1/T) and (lnk2, 1/T)

isothermaltemperature/℃ln(k1/s-1)E1/kJ·mol-1ln(A1/s-1)R21ln(k2/s-1)E2/kJ·mol-1ln(A2/s-1)R22112-10.837114-10.709120-10.270124-9.89392.1718.030.992-5.878-5.776-5.473-5.23776.4018.000.997
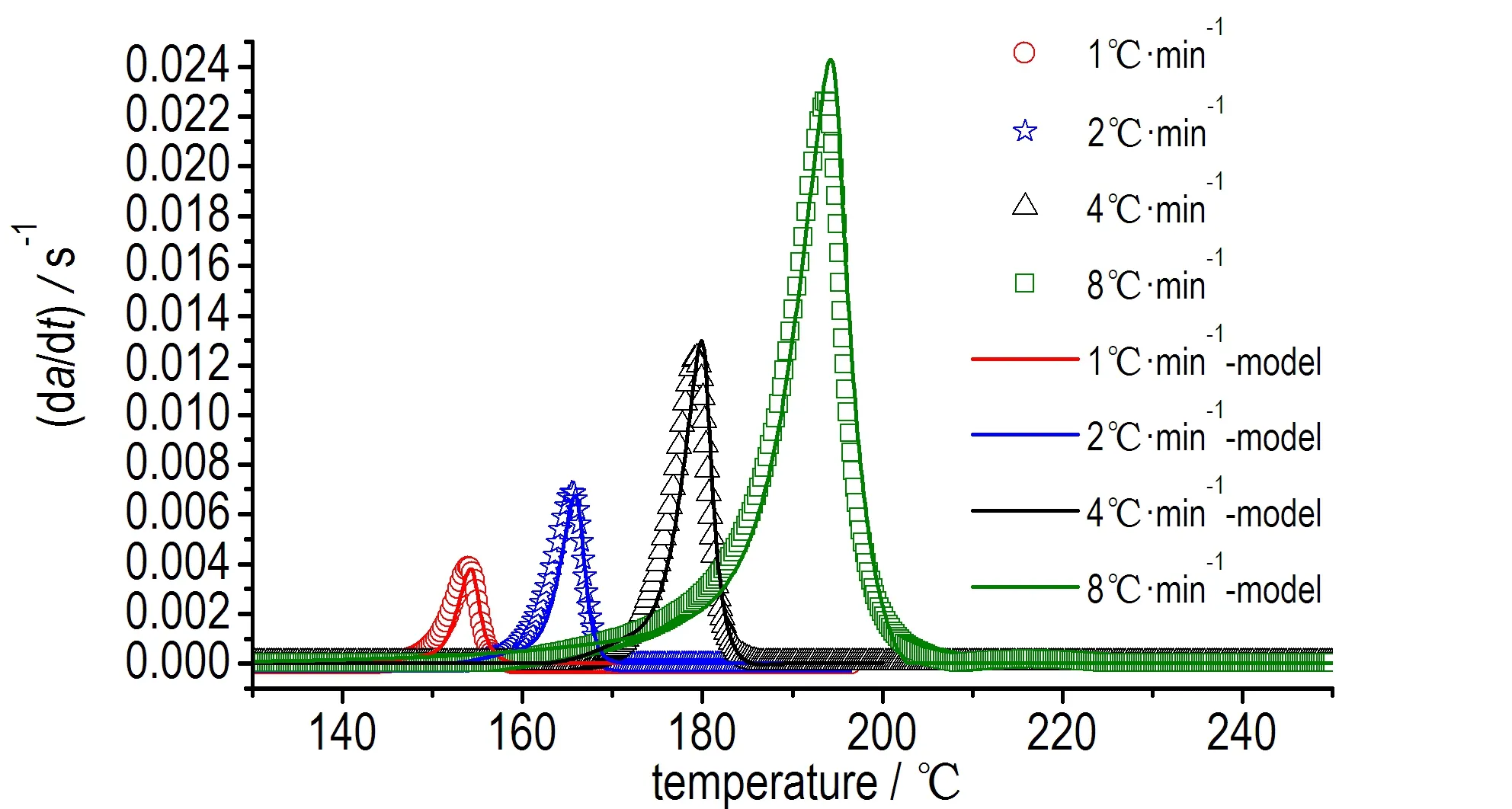
图5 模型拟合曲线和动态模式实验曲线
Fig.5 Comparison of model curves with dynamic DSC data
4 结 论
(1)硝基胍水溶液的动态及等温DSC实验表明,在动态模式下其起始分解温度较高(149~185 ℃),平均比放热量约为311 J·g-1; 等温模式下溶液平均比放热量约为305 J·g-1,与动态结果非常接近。
(2)基于Friedman法计算得到两种测试模式下获得的活化能很接近,表明其分解反应可用单步的反应速率描述。
(3)硝基胍水溶液的热分解为单步自催化反应,其分解动力学模型为:
dα/dt= exp(18.03)exp(-92170/RT)(1-α)1.111+
exp(18.00)exp(-76400/RT)(1-α)1.111α1.995,
该模型不仅可以准确描述其等温分解过程,同样可以描述动态分解过程。
参考文献:
[1] 段卫东, 吕早生. 硝基胍炸药的机械感度和爆炸性能研究[J]. 含能材料, 2003, 11(4): 209-212.
DUAN Wei-dong, LÜ Zao-sheng. Mechanical sensitivity and explosive performance of nitroguanidine(NQ)-based composite explosives[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2003, 11(4): 209-212.
[2] 魏学涛, 赵颖,李乃勤, 等. 新型硝基胍发射药研究[J]. 火炸药学报, 2001 (4): 34-36.
WEI Xue-tao, ZHAO Ying, LI Nai-qin, et al. The study on a new kind of Nitroguanidine propellant[J].ChineseJournalofExplosivesandPropellants, 2001 (4): 34-36.
[3] 周诚, 陈智群, 黄新萍, 等. 硝基胍标准物质的制备及其均匀性和稳定性研究[J]. 化学分析计量, 2009, 18(5): 4-6.
ZHOU Cheng, CHENZhi-qun, HUANG Xin-ping, et al. Preparation of reference material of NQ and study of itshomogeneity and stability[J].ChemicalAnalysisandMeterage, 2009, 18(5): 4-6.
[4] 俞朝晖, 栾志杰. 硝基胍火药的热安定性研究[J]. 火炸药学报, 1996 (4): 14-16.
YU Zhao-hui, LUAN Zhi-jie. A Investigation of hermal Stability of Nitroguanidine Propellants[J].ChineseJournalofExplosivesandPropellants, 1996 (4): 14-16.
[5] Liu Z R. Thermal analysis for energetic materials[M]. Beijing: National Defense Industry Press, 2008.
[6] http://www.somsds.com/detail.asp?id=-2142056035[2016-04-14].
[7] Liu Z R, Wang C Y, Kong Y H, et al. Investigation of the thermal stability of nitroguanidine below its melting point[J].ThermochimActa, 1989, 146: 115-123.
[8] Lee P P, Back M H. Kinetic studies of the thermal decomposition of nitroguanidine using accelerating rate calorimetry[J].ThermochimActa, 1988, 127: 89-100.
[9] Lee P P, Back M H. Thermal decomposition of nitroguanidine[J].ThermochimActa, 1989, 141: 305-315.
[10] Yan C L, Cheng Y. Investigation on the thermal stability of nitroguanidine by TG/DSC-MS-FTIR and multivariate non-linear regression[J].JThermAnalCalorim, 2010, 100: 949-953.
[11] 洪三国,傅孝愿. 硝基胍热解反应途径的t子化学研究[J]. 物理化学学报, 1991, 1(7): 30-34.
HONG San-guo, FU Xiao-yuan. A quantum chemical study of the mechanism of thermolythsis of nitroguanidine[J]. Acta Phys.Journalofphysicalchemistry, 1991, 1(7), 30-34.
[12] Liu Z R, Wu C Y, Yin C M. The thermal decomposition of nitroguanidine and some derivatives[J].SympChemProblConnectedStabilExplos, 1988, 8: 369-389.
[13] Volk F. Decomposition behavior of nitroguanidine[J].SympChemProblConnectedStabilExplos, 1982, 6: 373-414.
[14] UN Recommendations on the Transport of Dangerous Goods, Manual of tests and criteria, 5th revised edition, 2007.
[15] Vyazovkina S, Burnhamb A K, Criadoc J M, et al. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data[J].ThermochimActa, 2011, 520: 1-19.
[16] Friedman L H. Kinetics of thermal degradation of char-forming plastics from thermogravimetry application to a phenolic plastic[J].JPolym,Sci, 1964, Part C(6): 183-195.
[17] Bertrand R, Marco H, Patrick F, et al. Thermal decomposition of AIBN, Part B: Simulation of SADT value based on DSC results and large scale tests according to conventional and new kinetic merging approach[J].ThermochimActa, 2015, 55: 1-8.
[18] Elena M. Thermal decomposition of AIBN Part C: SADT calculation of AIBN based on DSC experiments[J].ThermochimActa, 2015, 11: 1-13.
[19] Li X R, Wang X L, Koseki H. Study on thermal decomposition characteristics of AIBN[J].JHAZARDMATER, 2008, 159: 13-18.
[20] Bertrand R, Marco H, Patrick Folly, et al. Prediction of thermal stability of materials by modified kinetic and model selection approaches based on limited amount of experimental points[J].ThermochimActa, 2014, 579: 31-39.
