基于鲁棒H∞理论的三级倒立摆控制系统研究
2017-05-08夏炎谢玮��
夏炎 谢玮��
摘要:为了研究三级倒立摆的鲁棒控制方法,设计出三级倒立的状态反馈H∞控制器。仿真结果表明三级倒立摆具有良好的鲁棒稳定性、鲁棒性、抗干扰性,实现了对三级倒立摆的稳定控制。同时运用了状态空间极点配置法和LQR最优控制法,分别设计出针对三级倒立摆的控制器。经比较研究:采用状态反馈H∞方法设计的三级倒立摆控制器的控制效果非常好,使其具有较小的振荡和超调量,倒立摆起摆迅速,稳定控制性能优良。
关键词:H∞控制理论;三级倒立摆;状态反馈;控制器
中图分类号:TP273文献标识码:ADOI:10.3969/j.issn.10036199.2017.01.004
1引言
三级倒立摆作为控制理论研究和进行各种控制实验的一个理想实验平台[1],对其不确定性的研究,在理论和实践上都具有重要研究意义。倒立摆具有变量多、阶次高、不稳定、非线性和强等特性[2],使得现代控制理论研究者把它作为研究火箭垂直姿势、双足行走机器人等控制对象的简单模型[3]。对倒立摆的研究应用到了多种技术并且涉及多个领域,包括机器人技术、计算机控制技术、控制理论技术等,试图通过对倒立摆的研究来检验控制理论在多变量、不稳定系统上的应用能力,从而找出最优的控制方法[4]。本文是基于鲁棒H
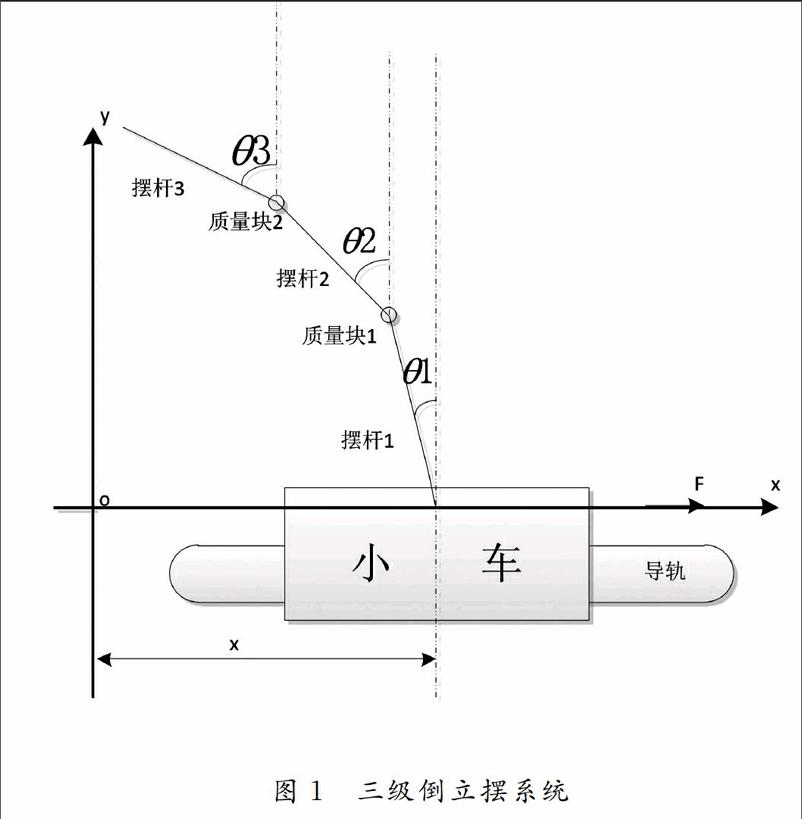
设定倒立摆的摆杆为刚體,控制系统的输入为电动机的输出力矩。三级倒立摆变量名称及系统模型参数见表1。利用动力学知识以及拉格朗日方程,可以建立起三级倒立摆的数学模型。结构图中的θ1,θ2,θ3为1、2和3级摆杆与垂直方向的夹角,其中g为重力加速度,g=9.8N/kg,F:电机对小车的驱动力
当给定初始状态为平衡态时即X=0时给系统加入单位阶跃响应信号,如图3所示,大约在10s时小车基本处于静止状态,趋于稳定。摆角1,2,3的振荡幅值大约为0.4rad且在5s后趋于稳定。为了通过对比验证,在相同的初始状态下,给系统施加一个脉冲信号作为扰动输入W的输入信号,如图4所示,虽然小车的摆角1,2,3的摆动幅度很大且振荡频率增大,但在10 s的时候小车静止,4s后摆角基本停止振荡,系统又能够重新回到平衡态,趋于稳定状态,说明系统具有很好的抗干扰能力。状态反馈H∞方法能够很好的控制倒立摆的摆角和小车的位置。
当给定初始状态为X=[1 2 -1 2 1 1 2 2]时,显然三级倒立摆系统是远离平衡态X=0的,这时给系统加入单位阶跃响应信号后如图5所示,即使系统振荡的幅度和频率很大,但最终还是能在5 s的时候回到平衡态使系统趋于稳定,具有很好的鲁棒性。4.2三种控制方法比较研究
为了比较研究,又设计了基于LQR[12]-[13]和极点配置算法的三级倒立摆控制器,并进行了仿真比较研究。如图6所示:
初始状态为平衡态即X=0时加入同样的单位阶跃响应信号情况下,基于LMI鲁棒H∞控制方法设计的倒立摆控制器具有很好的鲁棒稳定性和鲁棒性,虽然调整时间ts比另两种方法的较长,但符合系统要求。摆角1,2,3的振荡幅值和频率较小,超调量明显比其他两种方法小得多,摆杆的摆动幅度也比较小,调节时间和上升时间比较短。通过对比三种方法;基于LMI鲁棒H∞控制方法构造的控制器可以很好的控制倒立摆,使其有更好的鲁棒稳定性、鲁棒性和抗干扰性。
5结论
对三级倒立摆进行了鲁棒控制问题的研究。通过对比仿真实验,从系统鲁棒性和鲁棒稳定性两个角度综合的论证了状态反馈H∞方法的优点。
在仿真过程中,小车的位移和摆杆与竖直方向的夹角的初始值对倒立摆的稳定性影响很大,而在求取鲁棒H∞控制器的过程中,加权矩阵C1的选取对控制器的控制效果影响比较显著,现在没有具体的方法来选取合适的加权矩阵C1,只能根据经验来反复选取,这也是未来值得探索的方面。
参考文献
[1]SIEBER J,KRAUSKOPF B.Complex balancing motions of an inverted pendulum subject to delayed feedback control[J]. physica dnonlinear phenomena, 2004,197(3-4):332-335.
[2]王俊.基于倒立摆的PID 控制算法的研究[J].现代电子技术,2012,35(23):152-154.
[3]ASTROM K J,FURUTA K.Swinging up a pendulum by energy control[J]. Dans IFAC,13th Word Congress, San Francisco,1996.
[4]王强,陈炜,赵新华.直线倒立摆的快速起摆与稳摆控制研究[J].机械设计与制造,2013(5):74 - 77.
[5]张晋.时滞系统的H∞鲁棒控制策略研究[D].兰州:甘肃工业大学控制理论与控制工程专业.2000.40-65.
[6]FRANCIS B A, HELTON J W, ZAMES G.H∞ optimal feedback controllers for linear multivariable systems[J].IEEE Trans.Automat.Control,1984,29(10):888-900.
[7]俞立.鲁棒控制一线性矩阵不等式处理方法[M].北京:清华大学出版社,2002.6-267.
[8]高云霞. 基于H∞理论的主汽温控制系统的分析与综合[D].保定:华北电力大学自动化系,2005.25-34.
[9]申铁龙.H∞控制理论[M].北京:清华大学出版社,1996.
[10]薛定宇,陈阳泉.控制数学问题的MATLAB求解[M].北京:清华大学出版社,2007:411-414.
[11]薛定宇.控制系统计算机辅助设计(第二版)[M].北京:清华大学出版社,2006,87-90.
[12]王仲民,孙建军,岳宏.基于LQR的倒立摆最优控制系统研究[J].工业仪表与自动化装置,2005,3(1):6-8.
[13]郝智超,朱廷焕,刘克平.不确定柔性倒立摆系统鲁棒控制器设计[J].吉林大学学报:信息科学版,2009,27(6):
第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36,No1Mar. 2 0 1 7第36卷第1期2017年3月计算技术与自动化Computing Technology and AutomationVol36,No1Mar. 2 0 1 7
