考虑压实质量影响的碾压混凝土坝层间结合质量动态评价研究
2017-05-07钟登华鄢玉玲吴斌平
钟登华,鄢玉玲,崔 博,吴斌平,胡 炜,吕 鹏
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
1 研究背景
碾压混凝土坝筑坝技术是由美国的Laphael于1970年首次提出,并被广泛应用于许多地区。碾压混凝土的施工方法是通过机械的强力振动和碾压的共同作用,对超干硬混凝土进行压实,由于采用机械分层的施工方式,这种坝型存在层间结合面[1]。因此,层间结合质量成为了碾压混凝土坝施工质量控制的关键,这也是碾压混凝土坝不同于其它坝型的地方。层间结合质量一般通过抗剪强度、抗拉强度以及渗透性等指标来表征[2],这些指标一般通过钻孔取芯等现场试验获取,然而个别取样点的层间结合质量并不能代表全仓面的层间结合质量。实时监控系统[3-4]能够很好地监控施工过程中的层间间隔时间等施工参数,为碾压混凝土坝层间结合质量的控制提供了保证。因此,开展基于实时监控系统的碾压混凝土坝层间结合质量动态评价研究是控制碾压混凝土坝层间结合质量的有效手段。
层间结合质量的影响因素主要包括层间间隔时间、层面处理和压实情况等,目前的研究大都集中于研究层间间隔时间以及层面处理对层间结合质量的影响。姜福田[5]研究分析了层面对于各项力学性能指标的影响,为如何改善层间结合质量提供了依据;娄亚东[6]则通过试验分析了不同的层间间隔时间和不同的层面处理对碾压混凝土的抗剪强度和抗渗性能的影响,为提高碾压混凝土的层间结合质量提供了依据;Sanghyun Chun等[7]通过建立三维有限元模型,模拟了不同的层间结合条件对沥青路面的层间结合质量的影响;Li Sheng等[8]通过动态力学性能评价等角度,分析了4种沥青材料的层间结合质量,为改良沥青层间结合提供了依据;Yuan Zongzheng等[9]通过进行抗拉强度和切变强度试验,证明了增加有机纤维和高分子材料可以增强混凝土的层间结合质量。由此可见,现有的研究多是立足于层间间隔时间以及层面处理对层间结合质量的影响,研究采用何种措施、何种材料来改善层间结合的质量,而缺乏考虑压实质量影响的层间结合质量评价模型的研究。由于实际工程中,层间结合质量通过个别取样点进行监测,有限且随机的取样点使得据此评价得到的层间结合质量具有随机性和灰色性等不确定性,且取样监测方法为事后控制措施,不能对层间结合质量进行实时动态的评价,因此,需要建立一个能够综合考虑压实质量以及不确定性的碾压混凝土坝层间结合质量动态评价模型,加强对层间结合质量的控制。
针对上述问题,本文开展考虑压实质量以及不确定性影响下的碾压混凝土坝层间结合质量动态评价研究。由于压实度通过核子密度仪检测,不能够获得全仓面的压实质量,故在对层间结合质量进行评价时需要对压实度进行计算,进一步考虑压实度计算过程中的不确定性影响。本文需要解决以下3个方面的问题:(1)如何计算压实度并考虑压实度计算中存在的不确定性问题;(2)如何考虑不同季节条件下,混凝土初凝时间不同的问题;(3)如何建立层间结合质量评价指标与影响因素之间的关系。
首先针对问题(1),提出利用极大熵准则改进的盲数理论对具有不确定性的混凝土特性参数进行处理,建立能够考虑不确定性问题的压实度计算模型,并将其计算结果应用于层间结合质量评价。由于盲数理论是基于未确知数学发展而来的不确定性信息处理理论,故能够对具有多种不确定性的信息进行处理,并已被应用于风险评价、水质评价和电网系统可靠度评价等各个学科和行业[10-13]。应用盲数理论处理随机性信息时需要对信息进行离散化处理,同时,在本文中引入极大熵准则来确定盲数的可信度,获得随机性最大的参数可信度分布,实现基于熵-盲数的不确定性参数处理和分析,并在考虑不确定性的基础上对压实度进行全仓面动态计算;其次,针对问题(2),提出构建时间差值指标,通过利用初凝时间与层间间隔时间的差值作为评价指标来提高评价模型在不同季节条件下的适用性问题;再者,针对问题(3),借助线性回归分析方法建立综合考虑层间间隔时间与压实度的层间结合质量评价模型。最后,结合实时监控系统,对某碾压混凝土坝某仓面的层间结合质量进行评价。
2 研究框架
根据获得的指标数据建立评价指标体系,在考虑压实质量及其不确定性的条件下,对碾压混凝土坝的层间结合质量进行评价,评价框架如图1所示。研究分为评价指标体系的建立、评价模型的建立以及模型应用输出。
(1)第一步,基于实时监控系统、取样检测、钻孔取芯等方式获得指标数据,建立评价指标体系。层间结合质量评价指标体系分为3个层次,第一层为研究目标:层间结合质量q。本文中,层间结合质量的评价指标为混凝土的抗拉强度,通过钻孔取芯的方式取样。第二层为层间间隔时间和压实度。层间间隔时间是影响层间结合质量的主要因素,可以通过实时监控系统获得。Zhong等[3]研究开发的实时监控系统,通过利用GPS、GPRS、传感器等先进技术,对层间间隔时间、碾压遍数等施工参数进行实时跟踪记录,从而实时地控制施工质量,与传统旁站等人工手段相比,该系统能够更加严格地控制施工质量,减少人为因素的干扰。层间间隔时间需要控制在混凝土的初凝时间以内,而混凝土的初凝时间会随着外界环境的变化而变动;因此,不同的季节需要对混凝土的初凝时间进行检测,以更好地控制层间结合质量。同时由于考虑压实质量对层间结合质量的影响,因此将压实度作为第二层的指标之一,压实度一般通过核子密度仪检测,而对于任意位置处的压实度需要通过各种施工参数以及混凝土特性参数进行评价获得。因此,第三层为影响压实度的各种参数,包括碾压参数(碾压遍数和碾压厚度等)和混凝土特性参数(VC值和Gs值等),碾压参数可通过实时监控系统获得,混凝土特性参数通过取样检测获得。
(2)第二步,建立压实度计算方法。利用极大熵准则对盲数理论进行改进,对具有不确定性的参数进行处理,结合非线性回归分析方法,提出基于熵-盲数的压实度计算方法,实现考虑参数不确定性情况下的压实度全仓面动态计算。
(3)第三步,构建层间间隔时间差值指标。考虑到不同季节条件下,混凝土的初凝时间不同,计算初凝时间与层间间隔时间的差值,故以计算得到的差值作为层间结合质量评价的指标,以提高评价模型在不同季节条件下的适用性。
(4)第四步,分析层间间隔时间以及压实度与抗拉强度的关系,建立考虑压实质量的层间结合质量评价模型,并基于实时监控系统实现全仓面动态评价。
(5)第五步,将提出的方法应用于实际工程,实现对碾压仓面的层间结合质量的动态评价,并通过对比分析,验证模型的有效性和优越性。
3 层间结合质量评价模型与方法
3.1 基于熵-盲数的压实度动态计算方法由图1中的评价指标体系可知,压实度受碾压参数(碾压遍数、碾压厚度)以及混凝土特性参数(VC值和Gs值)影响。由于:(1)取样点的随机性使得混凝土特性参数具有随机性;(2)有限的取样点使得获得的混凝土特性参数不能完全反映全仓面的压实情况,使其具有部分已知部分未知的特点,即具有灰色性;(3)根据取样获取的混凝土特性参数数据,可以获得该参数的分布区间以及参数在各个区间内的大致分布规律,但对于决策者而言,其信息仍然不完备,亦具有未确知性。因此,在对压实度进行预测时需要考虑这些不确定性。由于盲数理论能够对具有多种不确定性的信息进行处理,而极大熵准则能够最大程度地降低主观影响,并得到最佳的可信度分布,因此应用极大熵准则改进盲数理论,提出基于熵-盲数理论的压实度计算方法,在考虑随机性、灰色性、未确知性等不确定性的基础上对压实度进行计算。
3.1.1 盲数理论 盲数理论是在概率统计、模糊数学、灰色系统理论、未确知数学基础上发展而来的理论,能够处理复杂的信息。中国工程院院士王光远教授的“未确知信息及其数学处理”一文,开创了未确知信息数学表达和数学处理研究的先河,在他的倡导下,刘开第等[14]对不确定性信息的数学处理方法进行了研究,总结出了盲数理论。
混凝土特性参数x是碾压混凝土坝压实度的某个具有不确定性的影响参数(比如VC值或者Gs值),假设其在施工期间是在一系列区间xi(称为灰区间)内变化,若每个区间xi与可信度αi对应,则参数x可以用盲数形式表示,该盲数称为混凝土特性参数盲数[15],并定义如下:设g(I)为由某参数x的一系列区间xi构成的区间型灰数集,xi∈g(I)。若αi∈ [0,1],i=1,2,3,…,m,f(x)为定义在g(I)上的灰函数,且f(x)表示为:

称f(x)为一个混凝土特性参数盲数,是参数x的盲数表达形式,αi为f(x)的参数x取xi值时的可信度,称α为f(x)的总可信度,称m为f(x)的阶数。盲数理论定义了盲数的均值、期望以及运算。本文利用盲数理论对具有不确定性的参数进行处理,但传统的盲数理论在确定区间的可信度时,一般根据实测数据的分布情况来确定,可信度结果受制于数据量的大小和参数的不确定性,因此本文应用极大熵准则来确定盲数的可信度。
3.1.2 极大熵准则 熵是源于物理学的一个基本概念,信息论创始人Shannon引入了一个不确定性程度的概念,将信息熵作为对信息不确定性程度的量度。对于离散型随机变量,熵的计算公式如下:

那么Hn即为一个具有n个可能结果的系统所具有的不确定性,αi为第i个可能结果出现的概率。
在信息熵的基础上,Jaynes提出了极大熵准则[16-18],即在一定约束下,挑选熵极大化的分布作为选定的分布,这种分布是最为随机的分布,其能够提供最多的信息。本文引入极大熵准则来确定盲数理论的可信度值,获得参数最可能的可信度分布情况,可以使得参数信息最大化,不确定性程度最小。
3.1.3 基于熵-盲数的不确定性参数处理 应用极大熵准则确定参数的可信度分布步骤为,首先,根据参数A的实测数据计算整体均值E,并划分为n个区间,计算各区间均值ei,应注意使分布集中的数据划分在一个区间内;然后,按照极大熵准则,建立如下模型:
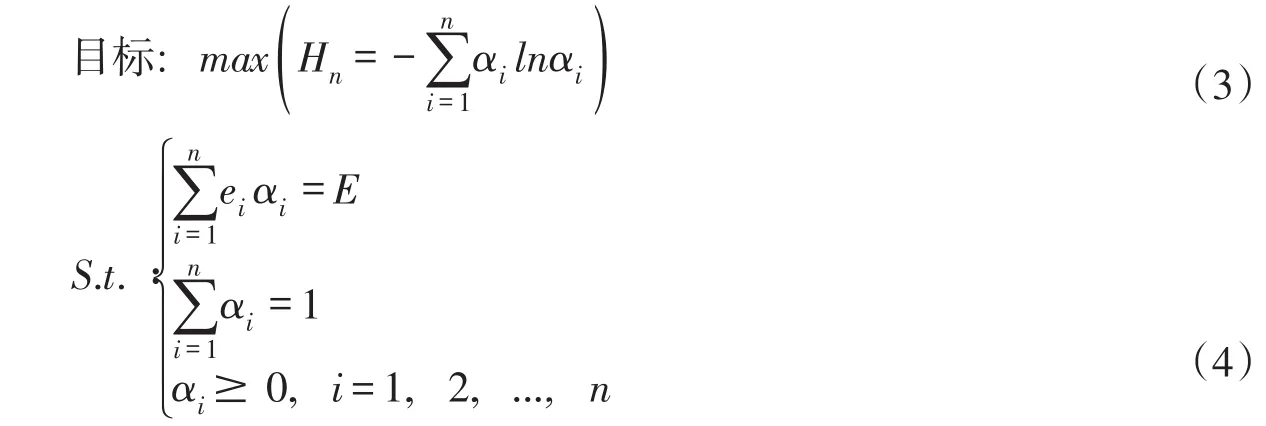
最后,根据拉格朗日乘子法计算各区间的可信度αi,从而可以构造压实度影响参数A的盲数形式:

式中:a、b分别为参数A的最小值和最大值;a1、b1为对应区间的边界值。
3.1.4 考虑参数不确定性的压实度计算 通过相关性分析建立压实度与各个参数的非线性回归关系,并将不确定性参数以盲数形式代入得到盲数形式的压实度计算结果,并应用于层间结合质量评价,从而在进行层间结合质量评价时体现压实度的不确定性。
3.2 考虑季节影响的层间间隔时间处理方法混凝土的初凝时间是指在标准条件下,从混凝土拌和加水起至贯入阻力仪贯入深度为25 mm所经历的时间。为了保证层面胶结处于最佳状态,务必在下层碾压混凝土初凝前完成上层铺料碾压,以便上层的骨料有可能嵌入到下层,形成犬牙交错,提高层间结合质量[19]。但是混凝土的初凝时间会随着外界环境温度的变化而变化,在高温季节,混凝土初凝时间较短,此时需要添加外加剂来延长初凝时间,这些因素使得混凝土的初凝时间在不同的施工时间段有所差异,而控制层间间隔时间的标准也会发生变化。因此,在进行层间结合质量评价时需要考虑不同的季节条件下,混凝土初凝时间不同对层间间隔时间控制的影响。
层间间隔时间可以通过实时监控系统实时获取任意位置的时间数据,而初凝时间则是通过试验获取。本文在不同的施工季节对混凝土的初凝时间进行了检测,8#—13#坝段的1426.5~1435 m高程范围内的仓面施工时间为7月和8月,由于增加了减水剂,其初凝时间分别为1134 min和914 min。为了提高层间结合质量评价模型在不同季节的适用性,在进行评价时,采用初凝时间与层间间隔时间的差值作为评价指标,如下式所示:

式中:T为初凝时间;t为层间间隔时间;∆t为两者差值,min。
3.3 考虑压实质量的层间结合质量评价模型根据上两节的方法,计算压实度和层间间隔时间差值,作为层间结合质量评价的指标,建立考虑压实质量的层间结合质量评价模型。以抗拉强度作为度量层间结合质量的评价指标,基于线性回归分析方法建立抗拉强度与层间间隔时间、压实度的映射关系,如下式所示:

式中:q为抗拉强度,MPa;∆t为初凝时间和层间间隔时间的差值,通过式(7)计算获得,min;P为压实度,%。
由于考虑了压实度的不确定性,因此,对层间结合质量进行评价的结果能够体现其不确定性。
4 工程应用
某碾压混凝土坝是位于中国西南地区的Ⅰ等大(1)型水利水电工程。大坝共分20个坝段:1#—7#为右岸非溢流坝段;8#—11#为溢流及泄洪放空底孔坝段;12#—15#为左岸非溢流坝段;16#—20#为进水口坝段。坝体混凝土总量366.77万m3,其中常态混凝土91.48万m3,碾压混凝土275.29万m3。本文以该工程8#—13#坝段的1426.5~1435.0 m高程范围内的仓面为研究对象,对该碾压混凝土坝的层间结合质量进行评价。通过实时监控技术、取样检测等方法获得142组碾压混凝土坝仓面指标数据,据此构建层间结合质量评价模型,实现在考虑压实质量及其不确定性的基础上对碾压混凝土坝层间结合质量的评价。其中前120组数据为回归样本,后22组数据为检验样本,其碾压混凝土强度等级为C25,抗拉强度设计值为1.27 MPa。
4.1 评价模型的建立
4.1.1 基于熵-盲数的压实度计算模型
(1)压实度非线性回归模型的建立。通过相关性分析确定压实度与各影响指标之间的关系,通过MATLAB建立压实度的非线性回归模型,如下式所示:
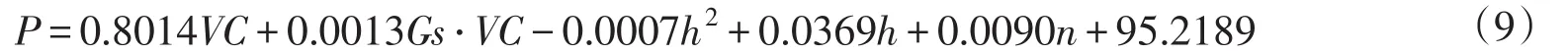
式中:P为压实度,%;VC为混凝土振至表面泛浆所需的时间,s;Gs为混凝土含气量;h为碾压厚度,cm;n为碾压遍数。
模型的最小误差平方和为10.7966,R2为0.7188。
(2)基于熵-盲数的不确定性参数处理。根据VC值和Gs值的实测数据分布情况,基于极大熵准则和盲数理论,对指标进行处理。以VC值为例,根据其实测数据将其划分为3个区间:[3.1,3.5]、[3.6,4]和[4.1,4.9],各个区间的均值分别为3.35、3.82和4.38,数据的总均值为3.94。然后根据前文所述,应用极大熵准则计算各个区间的可信度,从而建立VC值的盲数形式:

同理,建立Gs值的盲数形式:

据此可以对参数的不确定性进行分析。根据式(10)-式(13),实测的VC值变化区间为[3.1,4.9],区间宽度为1.8s,且落在3个子区间内的可信度差异值较小,而实测的Gs值变化区间为[3.3,4.7],区间宽度为1.4,略小于VC值的变化区间宽度,且落在[3.3,3.9]区间内的可信度为0.84,即能够以较大的可信度确定Gs值的取值区间,故认为其不确定性程度小于VC值。在实际工程中,应采取措施控制VC值的大小,以降低其不确定性程度。
(3)基于熵-盲数的压实度计算结果。将VC值、Gs值以盲数形式代入非线性回归模型式(9),得到基于熵-盲数理论的压实度计算模型为:

根据不同点的碾压参数即可得到各点的压实度情况。本文取可信度为0.9,此可信度可根据需要来选取,当可信度为0.9时,信息的损失在可接受的范围内[20],基于盲数理论压实度非线性回归模型的计算结果与实测值对比情况如图2所示。由图2可以看出,在可信度为0.9的情况下,压实度计算结果的可能值上、下界基本上能够包括真值,计算结果可行,模型可靠。

图2 基于熵-盲数的压实度计算结果(0.9可信度)
因此,基于熵-盲数理论的压实度计算结果为一个区间值,对于每一个样本,压实度值可能为上界值或下界值,也可能为区间内的任意一个值,其结果具有0.9的可信度;因此,在压实质量控制时,只要各个样本区间的压实度下界计算结果达到要求,则可认为该仓面在0.9可信度下压实质量合格。同时,可以将压实度计算结果的上界值和下界值的差值占可能结果区间的百分比作为评价结果的不确定性度量。本文压实度计算结果的上、下界的差值为1.32%,而实测压实度值的范围为[98%,100%],即认为压实度的所有可能结果位于这个区间,因此,将1.32与(100-98)做比值,计算结果为0.66,根据式(1)认为压实度计算结果存在大小为的不确定性。因此,对于每一个样本,压实度大小具体为区间内的何值具有不确定性,这一不确定性的大小根据上下界的差值确定为0.64,不确定性程度较大。由于压实度与各个指标之间的关系模糊,在无实测施工质量值时,通过相关指标来计算压实度,其结果必然具有不确定性。而基于熵-盲数理论的压实度计算方法既考虑了已知信息(即非线性回归模型是基于实测数值建立的),又考虑了不确定性信息(混凝土特性参数的熵-盲数处理),两者兼顾,相较于传统的单一数值结果,区间形式的计算结果既能够反映压实度计算过程中的确定性规律,又能够体现不确定性程度,包含了压实度计算中参数的灰色性、随机性等不确定性信息,更符合实际。
4.1.2 考虑压实质量的层间结合质量评价模型 根据式(7)计算初凝时间与层间间隔时间的差值,将其作为层间结合质量评价的指标。通过对抗拉强度与层间间隔时间差值、压实度进行Pearson相关性分析,结果如图3所示。图3中,主对角线的绿色柱状图为各个指标的分布频率直方图,右上方的蓝色散点图为各指标的数据分布散点图,同时给出了指标间的线性相关关系曲线,左下方为指标间相关性,颜色越深代表相关性越大。由图3可知,抗拉强度与层间间隔时间差值、压实度均存在较强的正相关关系,层间间隔时间一般要求控制在初凝时间以内,层间间隔时间越短,层间间隔时间差值越大,层间结合质量越好,而压实质量越好,层间结合质量也会越好;因此,相关性分析结果符合实际情况。根据散点图,利用MATLAB建立抗拉强度线性回归评价模型:

式中:q为抗拉强度,MPa;∆t=T-t为初凝时间T与层间间隔时间t的差值,min;P为压实度,%。
模型的最小误差平方和为0.4713,R2为0.8217,评价模型与相关性分析结果相吻合。实测值与模型拟合值的对比如图4(a)所示,二者的残差图如图5(a)所示。由图4(a)和图5(a)可知,模型拟合值与实测值的变化幅度基本吻合,二者残差基本都在0.1 MPa以内,仅仅10号和135号样本的残差较大,分别为-0.4和0.23 MPa,但整体来说满足精度要求。从整体的数据分布来看,实测的抗拉强度基本都介于2.6~3.2 MPa之间,均大于强度设计值1.27 MPa,层间结合质量合格。模型拟合得到的抗拉强度也都位于这个区间,仅10号和135号样本的实测抗拉强度超出了这个区间,因此,这两个样本的拟合误差较大。从抗拉强度的影响因素来看,10号样本的压实度为98.1%,初凝时间与层间间隔时间的差值为624.5 min,其压实度偏小,时间差值也较大,其实测的抗拉强度却是所有样本中的最小值,为2.3 MPa;135号样本的压实度为99.9%,初凝时间与层间间隔时间的差值为795.1 min,其压实度和时间差值均较大,实测的抗拉强度为所有样本中的最大值,为3.43 MPa,且远大于数据分布区间。从数据的角度分析,2号样本的压实度和时间差值(98.1%,629.4 min)与10号样本(98.1%,624.5 min)相近,二者的抗拉强度评价结果应当相近,但二者的实测抗拉强度相差较大,分别为2.62和2.3 MPa;101号样本的压实度和时间差值(99.9%,804.7 min)与135号样本(99.9%,795.1 min)相近,二者的抗拉强度评价结果应当相近,但实测结果相差较大,分别为3.1和3.43 MPa。这说明,层间结合质量评价系统较为复杂,相近的影响因素数据评价得到的抗拉强度也可能存在差异,具有不确定性,这种不确定性可能来自于压实度及其影响因素;故在实际工程中仅根据层间间隔时间以及采用单一数值的层间结合质量评价结果忽略了压实度的影响以及评价中的不确定性,其只能够提供确定性信息(层间间隔时间),忽略了不确定性规律信息(压实度及其不确定性),容易造成层间结合质量评价的误判,因此,有必要在考虑压实度及其不确定性的情况下,对抗拉强度进行评价。
根据上述分析,将基于熵-盲数的压实度计算结果代入上述层间结合质量评价模型中,得到考虑压实度不确定性的层间结合质量评价结果,如图4(b)所示。由图4(b)可知,考虑压实度不确定性的层间结合质量评价结果为区间形式,除了10号样本和135号样本,评价结果的上下界值能够基本上包含实测值;因此可以认为这两个样本的不确定性比其他样本的不确定性大;这说明通过层间间隔时间和压实度数据来评价10号和135号这两个样本的层间结合质量较其他样本差,得到的结果可信度较低,需要对其加强质量控制。从黄色区域的大小可以计算层间结合质量评价结果与实测结果相符的概率为0.31/(3.2-2.6)=0.52,根据式(1)可以计算由压实度不确定性带来的层间结合质量的不确定性大小为-[0.52×ln(0.52)+(1-0.52)×ln(1-0.52)]=0.69,即对抗拉强度进行监测时,监测结果落在黄色区域内的可能性为0.52,具有0.69的不确定性,不确定性较大,还有0.48的可能性出现超过3.2 MPa或者小于2.6 MPa的结果,因此,需要加强对不确定性参数的控制,降低不确定性程度,从而提高模型评价结果的可靠性。

图3 相关性分析与数据散点图矩阵
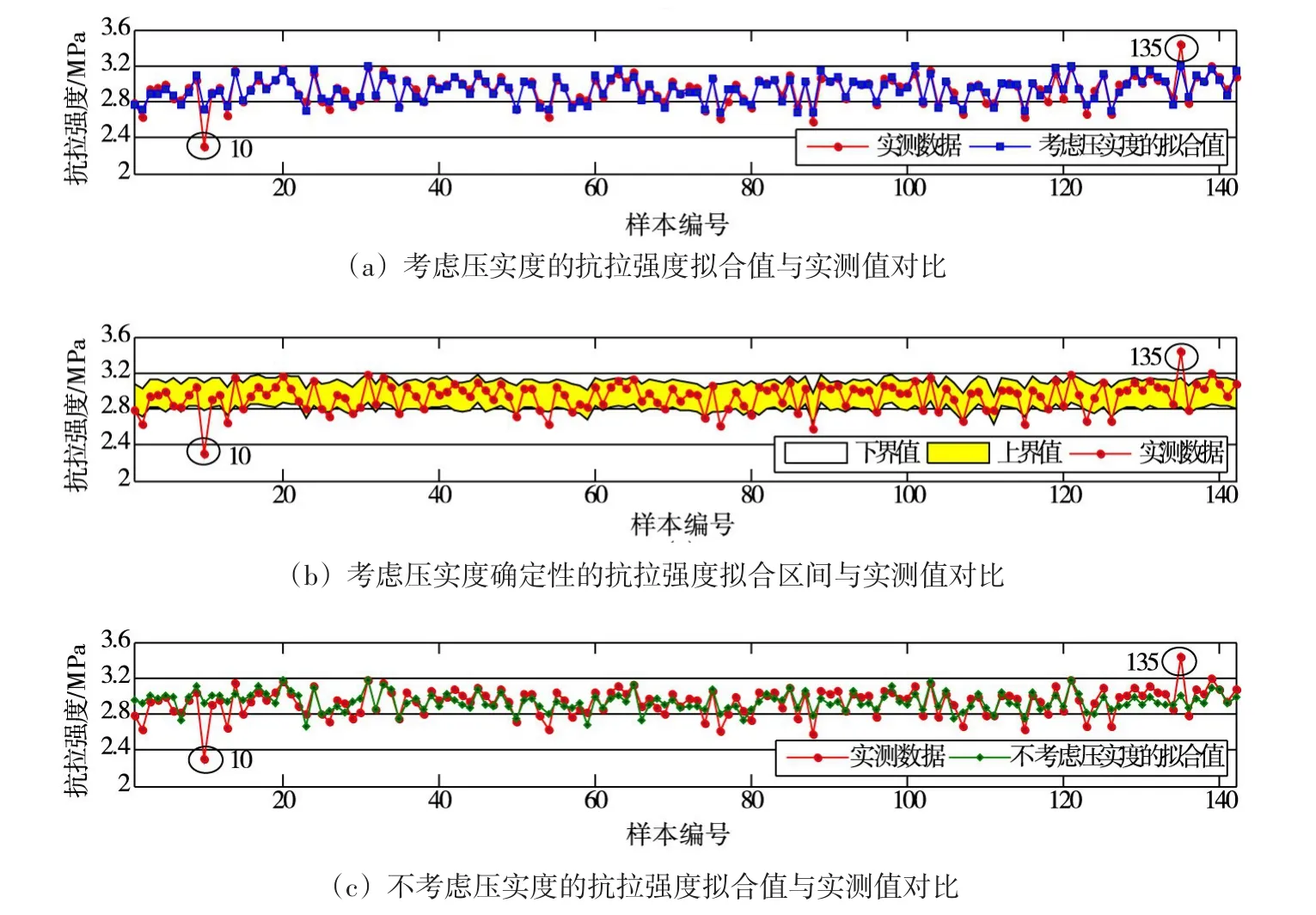
图4 实测值与拟合值的对比

图5 抗拉强度拟合残差
为验证本文模型的优越性,在不考虑压实质量情况下对层间结合质量进行评价,并将其结果与考虑压实质量的层间结合质量评价结果、考虑压实度不确定性的层间结合质量评价结果进行了对比分析,对比分析的实测值与拟合值的对比图以及拟合残差图分别如图4和图5所示。对比图4(c)和图4(a)可以发现,考虑压实度的抗拉强度拟合值比不考虑压实度的拟合值与实测数据更为相符;从残差对比图也可以得到相同结论,考虑压实度的抗拉强度拟合残差基本上远小于不考虑压实度的抗拉强度拟合残差;从整体的误差平方和计算结果分析得出不考虑压实度的抗拉强度模型的误差平方和为1.901,其大于考虑压实度的抗拉强度模型的误差平方和0.4713;因此,考虑压实度的抗拉强度模型评价结果更为准确。对比图4(a)和图4(b),考虑压实度不确定性的抗拉强度评价结果为区间值,这个区间能够基本上包含实测值,且通过区间的大小可以判断层间结合质量评价的不确定性大小,不确定性程度越大,说明由压实度计算带来的不确定性就越大,根据已知参数评价层间结合质量所提供的信息越少,需要在实际工程中加强对不确定性参数的控制,降低不确定性程度。同时,在实际工程应用时可以通过下界值来作为层间结合质量控制的标准,下界值是所有可能结果中的最小值,只要下界值能够符合规定的要求,则可以在0.9可信度下认为其层间结合质量满足要求。
4.2 实时监控下考虑压实质量的层间结合质量动态评价应用考虑压实度不确定性的层间结合质量评价模型对某碾压混凝土坝仓面进行评价。通过应用熵-盲数对混凝土特性参数的处理和在实时监控下对碾压混凝土坝仓面任意位置的压实度的动态计算,将熵-盲数的压实度动态计算结果应用于层间结合质量评价中,可以得到任意位置处的碾压混凝土坝层间结合质量评价结果,实现了对碾压混凝土坝层间结合质量的动态评价。
将某35 m×25 m的仓面划分成35个5 m×5 m的网格,通过实时监控系统获取仓面内各个网格的碾压参数和层间间隔时间,利用基于熵-盲数的压实质量评价模型计算其压实度,获得压实度计算结果。结合该仓面的施工季节确定其混凝土初凝时间为1134 min,据此,应用考虑压实度不确定性的层间结合质量评价模型计算其抗拉强度,通过应用盲数的上界值、下界值和均值对结果进行插值,从而绘制该仓面抗拉强度分布等值线图和云图。同时对比分析不考虑压实度影响下的该仓面的层间结合质量评价结果。图6表示初凝时间与层间间隔时间差值、不考虑压实度的抗拉强度等值线图,图7表示考虑压实度及其不确定性的抗拉强度等值线图和分布云图。
对比图6和图7可以得到以下结论:
(1)本文模型考虑了压实度及其不确定性对层间结合质量进行评价,评价结果更为精细和可靠。对比图6(a)和图6(b)可以发现,不考虑压实度的抗拉强度评价结果与层间间隔时间的分布情况基本相同,即不考虑压实度的抗拉强度评价结果完全依赖于层间间隔时间;而对比图6(b)和图7可以发现,考虑了压实度及其不确定性的抗拉强度的评价结果更为精细化,其能够对各个网格内的抗拉强度进行更为精细的评价,且不完全依赖于层间间隔时间的大小。即如图中的①网格,在不考虑压实度情况下认为该网格内的抗拉强度基本上为3 MPa左右,而考虑了压实度及其不确定性的抗拉强度评价结果显示,该网格内各点的抗拉强度具有较大差异,各点抗拉强度的上界值从2.9 MPa到3.1 MPa变化,下界值从2.6 MPa到2.8 MPa变化。又如②和③网格,其层间间隔时间相近,时间差值均为700 min左右,在不考虑压实度情况下认为两个网格的层间结合质量基本相同,但考虑了压实度及其不确定性情况下,这两个网格的层间结合质量评价结果并不相同,在实际工程中仅根据层间间隔时间来判断层间结合质量忽略了不确定性信息,层间结合质量评价结果是不可靠的即不能够体现在层间间隔时间相同的条件下层间结合质量也可能为不同的情况。故在实际工程中应当综合利用确定性信息(实测层间间隔时间)和不确定性信息(压实度及其不确定性)对层间结合质量进行评价。
(2)本文模型评价结果由上界值、下界值以及均值构成,并综合考虑了确定性信息和不确定性信息,其能够在提供抗拉强度评价结果的同时提供不确定性程度信息。本文的这种区间形式的结果更符合同一网格各点的抗拉强度具有差异性的实际情况。从各个网格的抗拉强度的上下界值的差值以及信息熵可以得到各个网格评价结果所具有的不确定性程度,而不确定性程度越大(大于0.6)的网格在实际工程中需要加强其质量控制。同时,在实际工程中,可以根据抗拉强度评价结果的均值分布情况,从而判断仓面层间结合质量的大致情况,判断各网格之间层间结合质量的优劣关系,如②网格层间结合质量优于③网格;亦可以根据下界值来控制其层间结合质量,即若下界值达到质量控制要求,则可以以0.9的可信度认为其层间结合质量符合要求,由图7的抗拉强度上下界值可知,该仓面的抗拉强度基本介于2.5~3.2 MPa之间,下界值满足抗拉强度1.27 MPa的要求;因此,本文认为该仓面的层间结合质量符合要求。
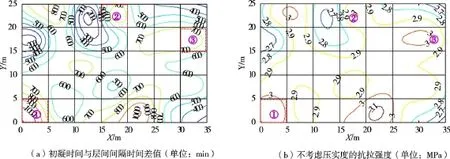
图6 某仓面时间差值与不考虑压实度的抗拉强度评价结果等值线图

图7 考虑压实度及其不确定性下的某仓面抗拉强度等值线图与分布云图(0.9可信度,MPa)
综上所述,本文模型能够综合利用确定性信息和不确定性信息对层间结合质量进行评价,从而为碾压混凝土坝的层间结合质量控制提供更多信息,能够有效且可靠地对碾压混凝土坝的层间结合质量进行动态评价。
5 结论
层间结合质量是碾压混凝土坝施工质量控制的重要因素,而影响层间结合质量的因素包括了层间间隔时间和压实度。本文提出了能够综合考虑这两个因素的层间结合质量评价指标体系,并在考虑压实度计算中存在的不确定性情况下对层间结合质量进行动态评价。首先,提出基于熵-盲数的压实度计算模型,实现了压实度影响因素的不确定性分析;其次,考虑不同季节条件下混凝土初凝时间不同,提出利用初凝时间与层间间隔时间的差值作为评价指标,并建立了综合考虑层间间隔时间与压实度的层间结合质量评价模型;然后,将本文评价模型的评价结果与不考虑压实度的层间结合质量评价结果进行对比分析,表明了考虑压实度的层间结合质量评价结果更为准确,且结合熵-盲数理论的应用,其评价结果不仅能够综合利用确定性信息,还能够根据评价结果的上界值、下界值来计算其不确定性,尤其对于不确定性较大的仓面,实际工程中需要加强其质量控制;最后,对研究区域某仓面的层间结合质量进行动态评价,评价结果表明,考虑压实度及其不确定的层间结合质量评价模型能够精细化地评价仓面的层间结合质量,其评价结果更为符合实际,同时,结合实时监控系统,应用本文模型能够实现碾压混凝土坝仓面的层间结合质量动态评价。
参 考 文 献:
[1] 魏日华,孙桂喜.碾压混凝土层间结合质量影响因素分析及改进措施[J].吉林水利,2006(S1):123-124,127.
[2] 王怀亮,宋玉普.多轴应力条件下碾压混凝土坝层面抗剪强度试验研究[J].水利学报,2011,42(9):1095-1101,1109.
[3] ZHONG Denghua,LIU Donghai,CUI Bo.Real-time compaction quality monitoring of high core rockfill dam[J].Science China Technological Sciences,2011,54(7):1906-1913.
[4] 吴斌平,崔博,任成功,等.龙开口碾压混凝土坝浇筑碾压施工质量实时监控系统研究与应用[J].水利水电技术,2013,44(1):62-65.
[5] 姜福田.碾压混凝土坝的层面与影响[J].水利水电技术,2008,39(2):19-21.
[6] 娄亚东.碾压混凝土层面处理对层间结合性能影响研究[D].杭州:浙江大学,2015.
[7] SANGHYUN Chun,KUKJOO Kim,JAMES Greene,et al.Evaluation of interlayer bonding condition on structur⁃al response characteristics of asphalt pavement using finite element analysis and full-scale field tests[J].Con⁃struction and Building Materials,2015,96:307-318.
[8] LI Sheng,HUANG You,LIU Zhao-hui.Experimental evaluation of asphalt material for interlayer in rigid-flexi⁃ble composite pavement[J].Construction and Building Materials,2016,102:699-705.
[9] YUAN Zongzheng,XU Fang,LIU Miao,et al.Interlayer bonding performance of organic fiber and polymer modi⁃fied cement concrete road overlay[J].Electronic Journal of Geotechnical Engineering,2014,19:10637-10647.
[10] 汪明武,李丽,金菊良.基于盲数理论的液化等级风险评价模型[J].岩土工程学报,2010,32(2):303-307.
[11] 赵书强,王海巍.基于盲数的配电系统可靠性评估[J].电力系统保护与控制,2011,39(16):7-12.
[12] 李如忠,洪天求.盲数理论在湖泊水环境容量计算中的应用[J].水利学报,2005,36(7):765-771.
[13] 唐晓娇.基于盲数理论的水体沉积物重金属污染评价模型[D].长沙:湖南大学,2013.
[14] 刘开第,吴和琴,庞彦军.不确定性信息数学处理及应用[M].北京:科学出版社,1999.
[15] 李如忠,王家权,钱家忠.地下水允许开采量的未确知风险[J].水利学报,2004,35(4):54-60.
[16] LI C,WANG S,WANG W.Reliability analysis of free jet scour below dams[J].Entropy,2012,14(12):2578-2588.
[17] 陈海涛,黄鑫,邱林,等.基于最大熵原理的区域农村干旱度概率分布模型[J].水利学报,2013,44(2):221-226.
[18] 钱龙霞,张韧,王红瑞,等.基于MEP和DEA的水资源短缺风险损失模型及其应用[J].水利学报,2015,46(10):1199-1206.
[19] 袁光裕,胡志根.水利工程施工[M].5版.北京:中国水利水电出版社,2009.
[20] 高赐威,程浩忠,王旭.盲信息的模糊评价模型在电网规划中的应用[J].中国电机工程学报,2004,24(9):24-29.
