基于模糊RES-云模型的坝基岩体可灌性评价研究
2017-05-07李晓超钟登华任炳昱邓韶辉祝玉珊
李晓超,钟登华,任炳昱,邓韶辉,祝玉珊
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
1 研究背景
大坝基岩灌浆(主要包括固结灌浆和帷幕灌浆)可以有效地改善坝基岩体的力学性能,提高坝基的整体性和降低坝基的渗透性等,大坝基岩灌浆作为坝基基础处理的有效措施被广泛地应用在国内水利工程中;岩体可灌性分析与评价是灌浆的基础,是灌浆设计时必须查明的基本条件,亦是选择灌浆材料和灌浆工艺的主要依据。因此,科学合理的可灌性评价对于保证灌浆效果具有重要的理论与工程意义[1]。国内外学者对可灌性做出了相应的定义[1-3],总体而言,可灌性指在压力作用下浆液渗透到被灌介质内的能力,以及浆液在被灌介质内的渗透能力。目前普遍采用的衡量岩体可灌性的方法是岩体压水试验。Ewert[4]、马国彦和林秀山[5]认为压水试验透水率大于特定值时岩体才具有可灌性,此时需要灌浆处理。Sadeghiyeh等[6]定性分析了可灌性与岩体渗透性的关系。Sohrabi-Bidar等[7]对灌浆量与透水率的定量关系进行了探讨。樊贵超[8]基于分形理论对注灰量与透水率的关系进行了探索性研究,并对灌浆区域进行可灌性类型划分。但是由于浆液和水的流变属性存在差异,并且岩体中裂隙分布具有复杂性和不确定性,浆液和水在岩体中的渗透扩散不完全相同;因此,可灌性和透水率之间并没有普遍适用的确定关系。此外,一些学者通过研究可灌性与可灌比(裂隙宽和水泥粒径之比)[9]、浆液属性[10]、耗浆率[1]以及岩体地质参数[7]等因素之间的关系对岩体可灌性进行了分析,Barani等[11]提出了基于节理间距和透水率的可灌性综合性指标。但是这些研究大多只对影响可灌性的单因素进行了分析,较少考虑多因素尤其是岩体地质因素对于可灌性的综合影响研究。因此,亟待建立综合考虑岩体地质特征和灌浆参数等因素综合影响的岩体可灌性分析与评价体系,这对于更加准确有效地进行岩体可灌性分析是十分必要的。
岩体可灌性的影响因素众多,包括浆液性质、灌浆工艺及被灌介质地质条件等诸多方面因素[3],并且这些影响因素间并不是独立的,它们存在相互影响,并共同组成一个复杂的系统。英国学者Hudson提出的岩石工程系统(Rock Engineering System,简称RES)理论[12]为解决此类复杂系统问题提供了新的途径。RES理论采用系统分析的方法,充分考虑多种因素以及它们之间的交互作用对整个岩石工程系统的影响,最终实现对岩体性态和工程效果的分析与评估。RES理论被广泛应用在岩土工程的各个领域,包括边坡稳定性评估[13]、地下工程稳定性评估[14]、崩落采矿工程崩落度评估[15]以及岩体爆破工程效果指标的评估[16]等。
RES方法研究多采用综合加权评价法,可以将分散的信息通过模型集成,再进行综合值的求和、分级,进而评价研究对象的综合水平。但是该方法存在以下不足:①影响可灌性的因素的权重决定于交互作用矩阵的编码,目前普遍采用的专家半定量法很大程度依赖专家知识,且多采用单一确定值表示二元作用,未考虑因素间交互作用的不确定性影响;②影响因素的指标等级划分、等级评值,评价综合指标取值范围、等级划分和评级具有很强的主观性;③无法识别单指标、总体指标与评价等级之间的隶属程度,遗漏了单个指标的一些评价信息;④当评价因子不能同时满足某一等级标准时未能合理处理评价因子的随机性问题;⑤评价因子实测值常因观测、计算误差或舍入等引起一定的误差,而这可能导致在阈值附近的因子等级划分不合理造成的评价分类模糊性问题。
可见,以上各问题实质是模糊性和随机性的综合分析问题,显然岩体可灌性评价不可避免地面临数据和指标的模糊性和随机性。云模型是李德毅等[17]提出的一种定性概念与其定量数值表示之间的不确定性转换模型,其已在数据挖掘、模拟预测和评价等多个领域得到应用。由于其在处理概念的模糊性和随机性方面的优势,大量学者将云模型应用在岩土工程领域的各类评价问题中,包括:岩体质量评价[18-19]、岩体稳定性分类[20]、岩爆烈度评估[21]、泥石流灾害危险性区划[22]以及水库诱发地震风险评价[23]等。
本文将云模型(Cloud Model)理论引入RES方法中,综合考虑评价过程中存在的模糊性与随机性问题,并采用模糊RES(Fuzzy RES)方法,即模糊专家半定量编码交互作用矩阵的方法对专家知识进行模糊化,从而降低专家半定量编码方法的主观性,建立基于模糊RES-云模型的岩体可灌性评价模型,实现坝基岩体可灌性的评价与分析。
2 坝基岩体可灌性评价指标体系
坝基岩体可灌性评价是一项复杂的系统工程,其准确性依赖于所建立的评价指标体系。影响坝基岩体可灌性的因素众多,这些影响因素可以分为3类:①地质条件,主要包括岩体岩性特征、结构面属性(节理裂隙产状、间距、延伸长度、粗糙度、张开度和充填情况等)、岩体结构特征、岩体完整性以及岩体透水性特征;②浆液性质,主要由浆液颗粒粗细、黏度以及浆液流变性等所决定;③灌浆工艺,主要包括灌浆压力、灌浆方法和灌浆设备等[1]。本文参考国内外有关研究成果[1,3,7],遵循代表性、存异性、系统性、易量化等原则,并综合考虑待评价灌浆工程实例情况,选取节理裂隙倾向、张开度、间距、延伸长度、粗糙度、填充情况、节理组系数、岩体质量指标RQD值、声波波速值、透水率、浆液水灰比以及灌浆压力等12个指标作为岩体可灌性的评价指标。其中,节理裂隙倾向、张开度、间距、延伸情况、粗糙度、填充情况和节理组系数能够反映岩体构造发育条件,描述被灌岩体中的空隙和缝隙的特征,是决定岩体的可灌性最重要因素;RQD值和声波波速是反映岩石结构特征和完整性的基本指标,RQD值越小、声波波速越小,岩体越破碎、裂隙越发育,消耗浆液越多,并且这两个易于获取,广泛应用于岩土工程领域评价中;岩体透水率反应岩体的渗透性,它是目前作为岩体可灌性判定的最主要指标,一般情况下透水率越大,岩体可灌性越好;由于浆液颗粒粗细、黏度以及浆液流变性参数获取困难,且其主要决定于浆液水灰比参数,故本文选用水灰比作为浆液性质的表征值;灌浆压力越大,浆液在压力作用下扩散距离越远,因此,灌浆压力同样是可灌性的重要影响因素。综上,建立坝基岩体可灌性评价指标体系,如图1所示。

图1 坝基岩体可灌性评价指标体系
3 基于模糊RES-云模型的坝基岩体可灌性评价模型
3.1 基于模糊RES-云模型的坝基岩体可灌性评价模型 建立了如式(1)至(4)的数学模型,该数学模型描述了基于模糊RES-云模型的坝基岩体可灌性评价系统,其中,基于RES理论建立综合考虑岩体地质特征和灌浆参数的岩体可灌性分析与评价体系;采用模糊RES方法降低了专家的个人经验和主观因素对评价结果的影响;引入云模型理论方法,建立坝基岩体可灌性模糊综合评价模型,能够更加准确有效地对岩体可灌性进行定量化分析和研究;数学模型包括目标函数、指标集、评价等级集、方法集。其中式(1)定义了评价系统的目标函数,fV表示可灌性指数GI与评价指标集X之间的复杂函数关系。式(2)定义了评价系统的指标集X,即上文建立的岩体可灌性评价指标体系。式(3)定义了各评价指标的等级集V和区间划分标准,包括五个等级:微可灌(V1级)、较可灌(V2)、中等可灌(V3)、容易可灌(V4)和强可灌(V5)。式(4)定义了求解目标函数所用的方法集M,其中Mcloud和MFRES分别表示基于云模型的模糊综合评价方法和模糊RES方法,R是云模糊隶属度矩阵,μ(xi,vj)表示指标xi对评价等级vj的隶属度,ω是求解指标权重集W的函数,f是求解评价结果集D的模糊综合函数。

3.2 基于模糊RES的综合评价方法 岩石工程系统(RES)理论是综合考虑岩石工程复杂特性的系统分析理论方法[12],该方法从确定研究对象的各影响因素开始,利用二元作用机理分析各因素之间的作用关系,采用交互作用矩阵对复杂的系统形态加以描述。通过对交互作用矩阵的非对角元素进行编码,并根据矩阵分析结果,实现系统主要因素的识别和重要性(即权重)的评估。RES理论的关键环节是交互作用构造与编码实现方式。
图2为考虑有n个影响因素(P1,P2,…,Pn)的交互作用矩阵,影响因素列于矩阵的主对角单元上,非对角单元Iij和Iji分别表示因素Pi对Pj的作用和因素Pj对Pi的作用,具体数值是通过矩阵编码得到的。将通过Pi所在的这一行的数列值累加,称之为原因C(Cause);同理将通过Pi所在这一列的数列值累加,称之为效果E(Effect),如式(5)和(6)。一个变量的原因代表这个变量对系统的影响,而一个变量的效果代表系统对这个变量的影响。因素Pi的交互作用强度值定义为原因和效果数值之和,并用其计算因素Pi在系统中的重要性(即权重wi),如式(7)。

图2 RES交互作用矩阵

所有影响参数的权重获得后,待研究问题的系统综合性指标(如本文所研究的岩体可灌性指标(GI))即可通过下式得到:

式中,Pi为各影响因素按照指标等级分类所赋予的等级特征值。
目前,交互作用矩阵编码最常用的是专家半定量法(ESQ),通过专家经验按照相互作用强度等级赋予不同的数值。影响因素间相互作用强度被赋予一个确定的数值,显然这种方式缺少对因素间交互作用的不确定性进行描述。国外学者Rafiee等[15]提出了一种考虑编码过程不确定性的模糊专家半定量编码(FESQ)方法,对于研究复杂的岩石工程系统问题有很好的效果。FESQ方法编码交互作用矩阵的步骤如下:
(1)建立交互作用矩阵,收集一定数量专家的半定量编码信息。
(2)利用模糊推理系统(FIS)对专家半定量编码进行模糊化。以各交互作用强度等级专家投票比例值作为模糊推理系统的输入,建立一定的模糊推理规则,最终输出模糊RES编码。
3.3 基于云模型的模糊综合评价方法 设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C的一次随机实现,x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数,则x在论域U上的分布称为云(cloud),每一个x称为一个云滴[17],即:

期望Ex(Expected value)、熵En(Entropy)和超熵He(Hyper entropy)是云的一组数字特征,其中:Ex是云滴在论域空间中的均值,代表概念量化的最典型样本;En表示云滴在论域空间中的离散程度,是定性概念的不确定度量;He是熵的不确定度量,由熵的模糊性和随机性共同决定。
基于云模型理论确定的云参数Ex,En和He,运用正向云发生器分别对评价指标生成对应的等级隶属度云模型,如图3所示,图中横坐标表示评价指标取值,纵坐标代表向对应等级的隶属度,从右侧到左则是I~V级对应的云。

图3 评价因子隶属于级别的云模型
依据云发生器的算法,计算某一评价指标数据x0隶属于某等级云的确定度:
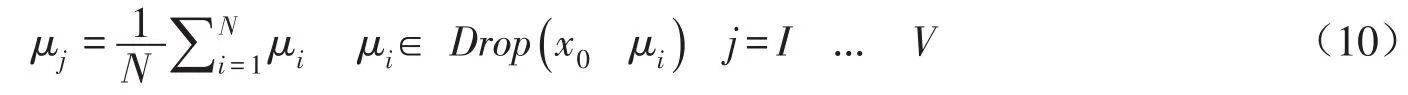
式中,μi为正向云发生器一次计算得到的指标数据x0隶属于某等级云的确定度;N为正向云发生器计算次数。
结合评价因子的权重,最终计算得到综合确定度U。根据最大的综合确定度值,判别样本的可灌性级别:
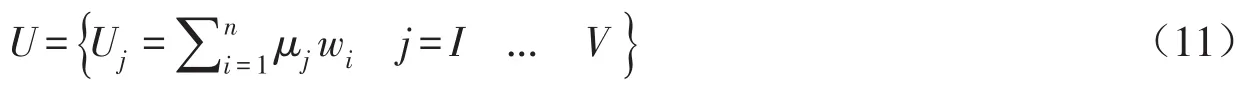
式中,Uj为评价样本隶属于等级j的综合确定度;wi是评价因子的权重。若则评价等级属于j0。
3.4 基于模糊RES-云模型的坝基岩体可灌性评价模型 基于模糊RES-云模型的模糊综合评价方法构建坝基岩体可灌性评价模型,其关键在于利用RES理论把整个岩体可灌性问题当作一个系统来处理,并充分考虑复杂地质和施工因素以及它们之间的交互作用,应用模型分析的方法,实现对岩体可灌性的分析与评估;采用模糊推理系统对RES交互作用矩阵进行模糊化处理,能够最大程度上降低专家的个人经验和主观因素对评价结果的影响;引入云模型理论方法,将每一个评价因子对应于可灌性等级的隶属度看作是一个云模型,通过构造隶属度函数的云模型可以考虑可灌性评价过程中的随机性和模糊性。利用模糊RES-云模型的岩体可灌性综合评价模型的具体实现流程如图4所示。
4 工程应用及结果分析
结合澜沧江流域某大型水电工程说明基于模糊RES-云模型的综合评价方法在水电站坝基岩体可灌性评价中的具体应用。研究对象为该水电工程坝基固结灌浆工程的灌浆施工单元。
4.1 坝基岩体可灌性评价指标分级标准 目前,涉及坝基岩体可灌性的研究中缺乏多影响因素下的岩体可灌性分析,且鲜有可灌性综合评价分级研究,可灌性评价指标分级标准尚无通用的准则可以遵循。参考可灌性相关研究[7,24-25]中关于岩体可灌性与影响指标间的一般规律,其中,节理倾向越缓,灌浆孔穿越的裂隙越多;隙宽越大、延伸长度越大、面越光滑且填充物少,浆液越容易进入且扩散距离越远;节理间距越小、节理组数越多,岩体裂隙越多;RQD越小、声波速度越小,岩体质量越差;透水率越大,岩体宽大导水裂隙越多;增大水灰比和增加灌浆压力能够提高浆液进入岩体的能力;综合以上条件,岩体可灌性越好。将坝基岩体可灌性划分为5个等级,即微可灌(Ⅰ级)、较可灌(Ⅱ级)、中等可灌(Ⅲ级)、容易可灌(Ⅳ级)和强可灌(Ⅴ级),并参考岩土工程评价领域惯例以及工程实例可灌性调查经验将各评价指标进行了等级划分,最终提出坝基岩体可灌性评价指标的分级标准,如表1所示。

图4 模糊RES-云模型的岩体可灌性综合评价模型

表1 坝基岩体可灌性评价指标的分级标准
4.2 坝基岩体可灌性评价模型求解
4.2.1 坝基岩体可灌性评价指标云模型的生成 根据评价指标的变化范围和评价等级的定义区间(表1),确定岩体可灌性评价指标云模型的各个参数,评价因子对某一可灌性等级的云数字特征按下式进行计算:

式中:Cmax和Cmin分别为某一等级标准的最大与最小边界;k值通常是人为给定的一个经验值[18-19],可以根据变量本身的不确定程度进行调整。综合考虑各变量的模糊阈度、变量指标数量级的差异以及实际观测时因观测、计算误差或舍入等引起的误差,节理裂隙倾向、张开度、间距、延伸长度、粗糙度、填充情况、节理组系数、RQD值等指标k值取0.15En;声波波速值、透水率、浆液水灰比以及灌浆压力等指标由于在测量方法上更为严格,在数据误差上较前者小,因此令其k值取0.05En。
基于云模型理论确定的云模型参数Ex,En和He,运用正向云发生器对坝基岩体可灌性评价因子生成相应的岩体可灌性等级隶属云模型,如图5为透水率的岩体可灌性等级隶属云模型。图中横坐标表示透水率的取值,纵坐标代表对应可灌性等级的隶属度,从左向右分别代表岩体可灌性等级Ⅰ级至Ⅴ级对应的云。

图5 评价因子(透水率)隶属于岩体可灌性级别的云模型
4.2.2 确定坝基岩体可灌性评价指标权重系数 采用模糊RES方法确定岩体可灌性影响指标权重。
(1)利用模糊专家半定量编码方法建立可灌性影响因素的模糊RES交互作用矩阵。选择10位具有丰富灌浆工程经验的专家进行意见咨询,内容为因素间相互作用编码(按照交互作用强度由小到大分为0~4五个等级值);对于交互矩阵每一个元素,按照专家对于交互作用强度判断进行统计:nA,nB,nC,nD,nE分别表示认为无交互作用,弱交互作用,中等互作用,强交互作用和关键交互作用的专家人数比例。这五个数值用作模糊推理系统的输入,每一个输入按照两个模糊集分类(“高”、“低”)。例如,当nA输入为“高”意味着大多数专家认为因素间无交互作用。这里认为比率数值低于0.4时,“低”集合的隶属度函数值较大,“高”集合的隶属度函数值小,反之亦然。对于模糊推理系统的输出同样定义为若干等级,将专家半定量编码中五等级编码(0到4)分为9个模糊集。建立如图6的模糊推理系统,系统有5个输入,每个输入两个节点,因此最多可定义25推理规则,除去不符合逻辑的规则,该模糊推理系统含有15条规则。比如,对于一个交互作用矩阵元素,6个专家认为是强交互作用,3个专家认为是关键交互作用,剩余1个专家认为是中等交互作用。模糊推理系统的输入即为:nA=0,nB=0,nC=0.1,nD=0.6,nF=0.3。通过模糊推理系统规则运算,可得到输出为3.14,即为该交互作用矩阵元素的模糊RES编码。同理可得交互作用矩阵全部元素编码。
图7为岩体可灌性评价因子节理倾向与其他评价因子间交互作用强度专家编码情况(图中柱状图表示的对于交互作用强度判断的专家人数比例),以及通过模糊推理系统获取的最终RES交互作用矩阵强度值(图中折线表示的模糊RES交互作用强度值)。表2为最终的坝基岩体可灌性模糊RES评价模型的交互作用编码值。可以看出,影响岩体可灌性的众多因素间存在复杂的关系,大部分因素交互作用值不等于0。这些因素共同构成了一个复杂的岩体可灌性评价系统。
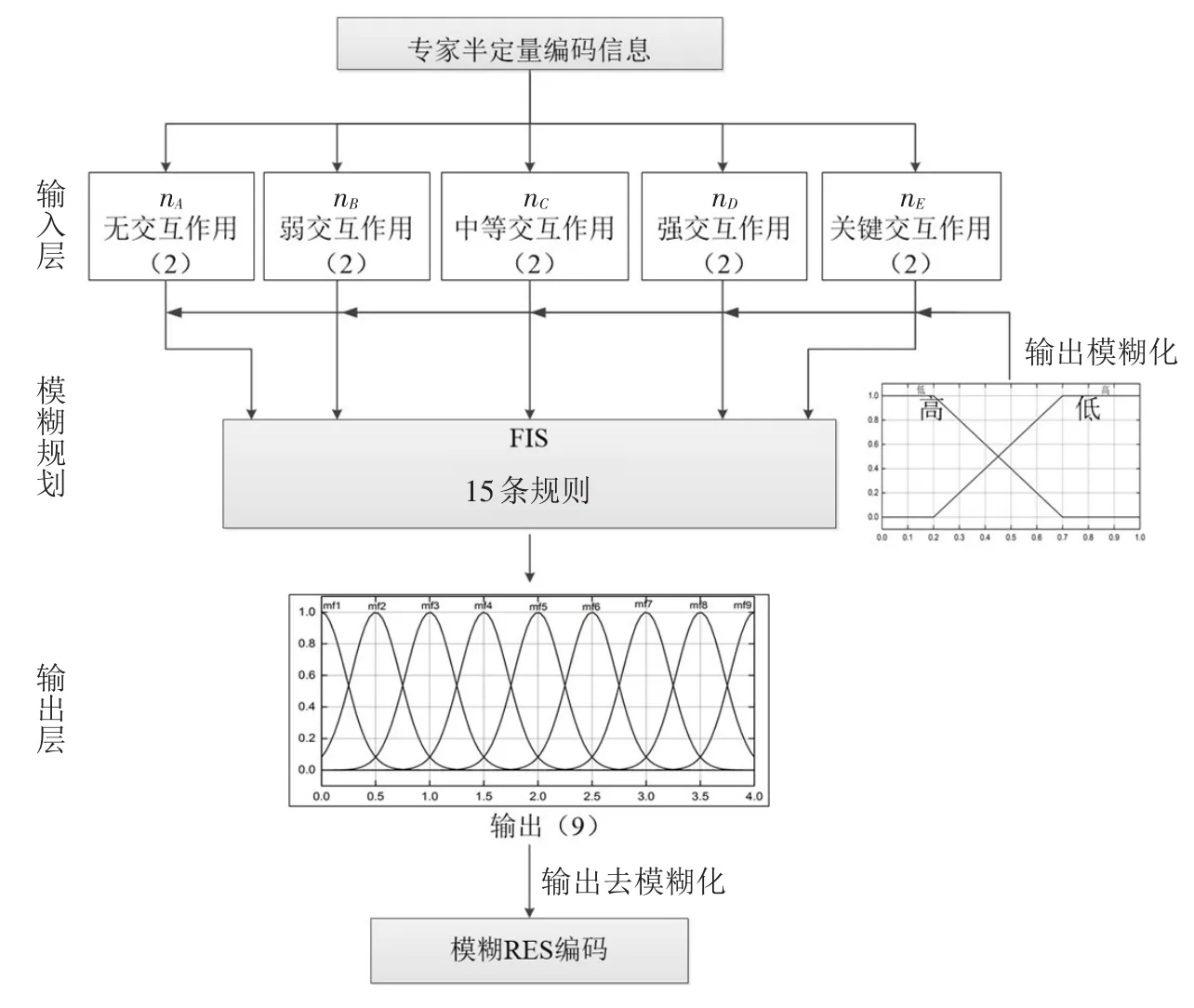
图6 交互作用的模糊推理系统结构

图7 节理倾向对于其他评价指标交互作用强度专家编码与模糊RES的交互作用强度值
通过对编码后的交互作用矩阵进行分析得到坝基岩体可灌性评价模型的作用-效果(C-E)图,如图8所示。各影响因素在因果空间的位置表明了各因素的交互作用模式,在C=E线以上的因素具有较次的优势参数,而在C=E线以下的因素具有较大的优势参数。由图8可知,最大优势参数为灌浆压力,其对坝基岩体可灌性系统的影响最大;最次优势参数为浆液水灰比,其受到其它因素的制约较多。自C-E图左下角至右上角,随着C+E值的增加,因素对于整个系统的作用变得更重要。图8可以看出本文研究的12个影响因素间都具有一定的交互作用,它们是岩体可灌性评价中的重要评价指标。其中,透水率、RQD、灌浆压力、声波波速和节理张开度交互作用强度最大(右上角虚线框内),它们是影响岩体可灌性的最主要指标;节理组系数、节理倾向和浆液水灰比交互作用强度较小(左下角虚线框内),它们对于岩体可灌性评价重要性程度弱。

图8 岩体可灌性评价模型影响因素的C-E图
(2)确定岩体可灌性影响指标权重。通过各影响因素的C+E值,可以得到各影响因素的总要性程度,利用式(5)~式(8)计算各指标权重,结果如表2。
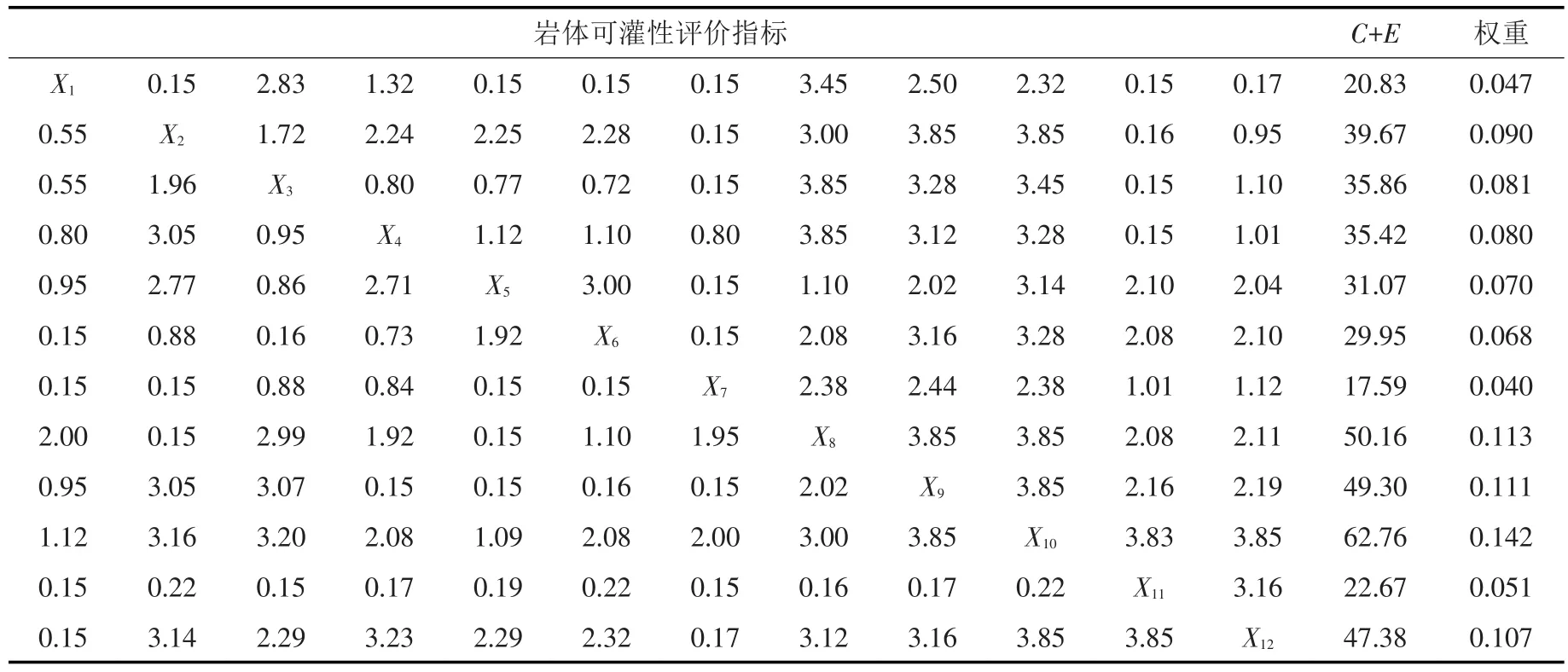
表2 坝基岩体可灌性模糊RES评价模型的交互作用编码
4.2.3 坝基岩体可灌性综合评价 选用的某水电站坝基固结灌浆代表性单元的各指标详细数据如表3所示。基于各评价指标的隶属度云模型和权重参数,利用模糊RES-云模型评价方法,计算各样本的可灌性等级综合确定度,基于确定度最大原则判断岩体可灌性等级,结果如表3所示。
由表3得到的坝基岩体可灌性评价结果可知,灌浆单元可灌性等级集中分布在Ⅲ~Ⅴ等级,表示该坝基灌浆单元岩体可灌性以中等可灌~强可灌起主导作用。并且,可灌性等级确定时,采用模糊评价的方法,能够得到评价样本隶属于各等级的隶属度,反映出岩体可灌性评价中的不确定性,为工程设计施工提供了更多决策信息。
4.3 坝基岩体可灌性评价结果分析 将本文综合评价模型得到的结果与单因素评价方法(以透水率为列)评价结果进行对比,选取大坝坝基水平河床坝段固结灌浆区域为例,如图9所示。可以看出综合评价模型结果与透水率单因素评价结果具有一定的一致性,表现在大部分灌浆单元可灌性等级评价一致,这是由于透水率作为可灌性评价关键指标,在评价过程中具有很大的重要性,从本文计算的权重中即可体现。图9中两种方法对于岩体可灌性等级评价存在差异的单元,主要是由于以单指标评价岩体可灌性,只考虑透水率指标作为评价依据,然而,由于水和浆液的流变属性存在差异,并且岩体裂隙具有复杂性和不确定性,可灌性并不能完全由透水率决定。本文采用的可灌性评价方法,全面考虑影响岩体可灌性的各种因素,包括地质条件、浆液性质以及灌浆工艺等各方面多因素,相比于单因素评价方法更具有全面性和合理性。
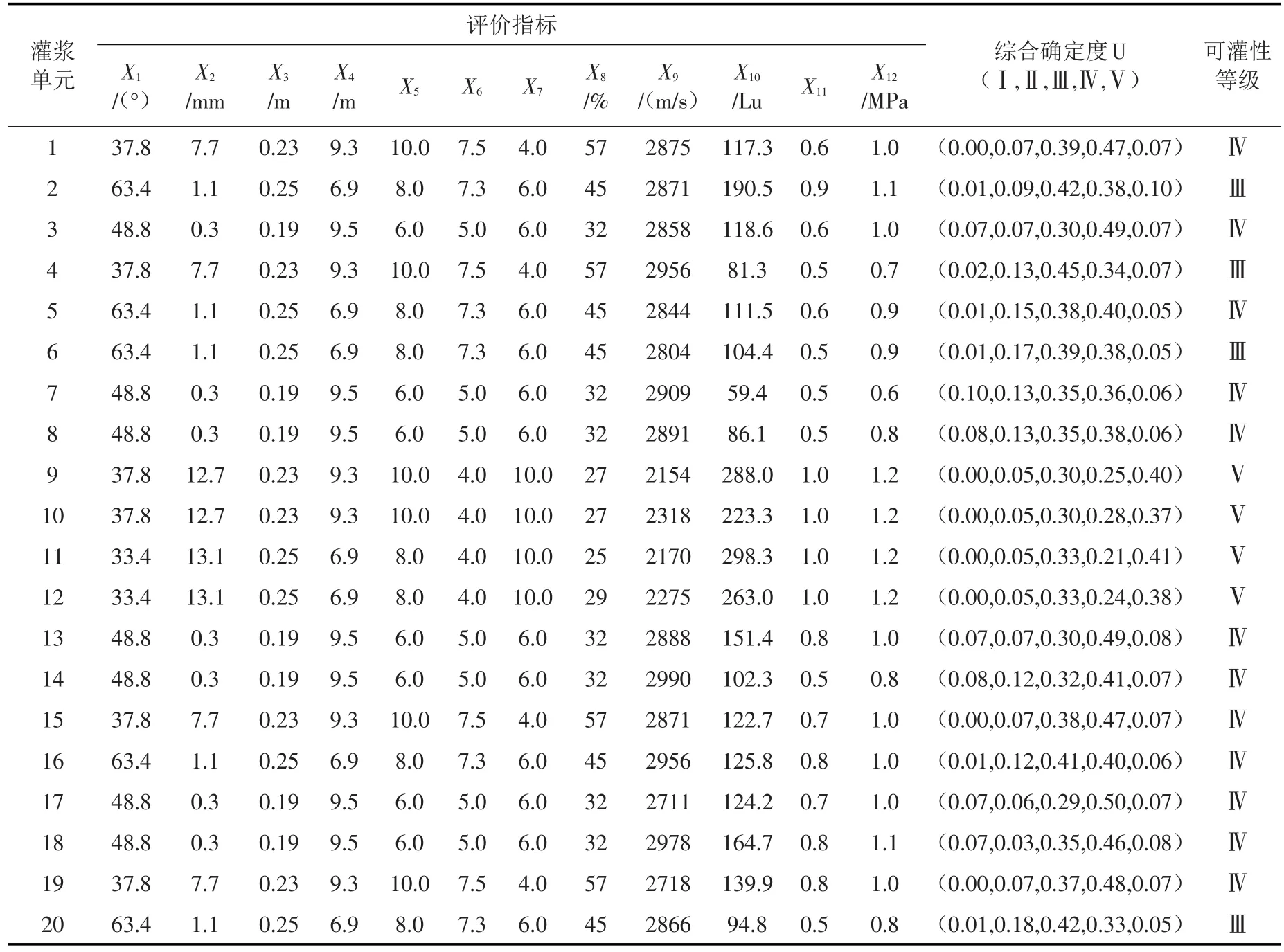
表3 灌浆单元评价指标数据与评价结果
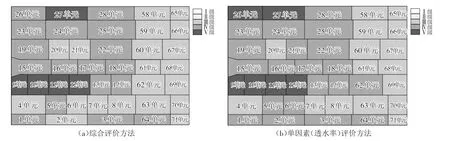
图9 综合评价方法与单因素(透水率)评价方法可灌性评价结果对比
基于模糊RES-云模型的坝基岩体可灌性评价方法提出一个表征岩体可灌性的综合性指标GI,形式如下式:

式中:Uj为评价样本隶属于等级j的综合确定度;Qj为等级特征值,这里定义Qj=j。
为了验证基于模糊RES-云模型的坝基岩体可灌性评价模型的合理性和有效性,本文将基于综合评价模型得到的表征岩体可灌性指标GI与灌浆单元实际单耗情况CT(Cement Take)值对比分析,并将模糊RES-云模型岩体可灌性评价模型与不考虑可灌性等级隶属关系不确定性的传统RES模型进行对比,即式(15)与式(8)计算得到的岩体可灌性指标(GI-RES&云模型与GI-RES)进行对比分析,如图10和图11所示。
图10中,通过岩体可灌性指标GI对灌浆单元的可灌性进行评价,模糊RES-云模型岩体可灌性评价模型与传统RES模型得到的可灌性指标与灌浆单元实测单耗情况都具有较好的一致性。模糊RES-云模型得到可灌性由高到低顺序为:9>11>10>12>19>15>1>2>18>17>13>3>16>5>4>6>14>8>20>7(数字代表单元编号,符号“>”表示可灌性排序优势关系),传统RES模型得到可灌性由高到低顺序为:11>9>10>12>2>1>15>19>18>5>16>3>13>17>6>14>4>20>7>8,两者与实际灌浆单元单耗情况基本一致(9>10>11>12>19>15>1>2>17>13>3>16>18>4>5>6>14>8>20>7)。

图10 岩体可灌性指标特征值GI与灌浆单元单耗CT对比
图11中,为研究GI指标与单耗的关系,以GI指标值为横坐标、实测单耗为纵坐标绘制散点图。可以看出两者之间存在很明显正相关关系,随着GI的增加,单耗随之变大。图11(a)中,当GI<65时,单位注灰量一般小于200 kg/m;当65<GI<70时,单位注灰量处于200~400 kg/m区间;当GI>70时,单位注灰量大于400 kg/m。将模糊RES-云模型岩体可灌性评价模型与传统RES模型获取的GI指标与实测单耗分别采用线性关系和二次多项式关系进行拟合。两种模型得到的GI指标值与实测单耗都具有很好的相关性,相关系数都在0.7以上。因此,基于模糊RES-云模型的坝基岩体可灌性评价模型的GI指标在一定程度上可以作为表征岩体可灌性的综合性指标。对两种模型进行对比,显然模糊RES-云模型无论是线性和二次多项非线性拟合得到的GI指标与单耗的关系都较传统RES模型优,其中线性拟合关系式相关系数分别为RRES-云模型=0.7821和RRES=0.7165,二次多项非线性拟合关系式相关系数分别为RRES-云模型=0.9623和RRES=0.8793。说明模糊RES-云模型较传统RES模型的优势在于考虑可灌性评价过程中的随机性和模糊性,更加科学合理,准确度高,贴合实际。对于GI指标与单耗的两种拟合模型(线性模型和二次多项式模型)分析可以看出,无论是模糊RES-云模型还是传统RES模型,二次多项式模型在相关性上都由于线性模型,说明岩体可灌性与评价指标间存在复杂的非线性关系。另外,基于GI指标与单耗回归模型的单位注灰量预测,可作为一种新的预测方法,对于现场灌浆施工控制也具有指导意义。

图11 灌浆单元单耗CT与岩体可灌性指标特征值GI关系
5 结论
针对目前涉及岩体可灌性评价的研究中多为考虑单因素影响下的岩体可灌性评价,未能充分考虑可灌性评价中的模糊和随机等不确定性问题,提出了基于模糊RES-云模型的坝基岩体可灌性评价模型与方法,并结合工程实例对岩体可灌性进行评价,得到以下结论:
(1)本文采用的可灌性评价方法,全面考虑影响岩体可灌性的各种因素,包括地质条件、浆液性质以及灌浆工艺等各方面多因素,相比于单因素评价方法更具有全面性和合理性。
(2)基于RES理论从系统的角度科学合理地确定评价因子的重要性程度,并获取指标权重。通过引入模糊理论克服RES方法中对主观因素的依赖,体现了评价对象的主动性,更加符合实际情况。
(3)本文将考虑模糊性和随机性关联问题的云模型理论引入坝基岩体可灌性的评价研究中,为坝基岩体可灌性评估提供了一种科学的方法。该方法能够反映出岩体可灌性评价中的不确定性,为工程设计施工提供了更多决策信息。
(4)模糊RES-云模型作为一种评价分析方法,在使用于岩体可灌性评价过程中关键在于建立完善的评价指标体系、合理选取评判因子和云数字特征以及科学确定各评价因子的权重,保证岩体可灌性的评价结果的准确性和可靠性。
参 考 文 献:
[1] 黄向春.岩体可灌性分析与评价综述[J].勘察科学技术,2000(4):36-41.
[2] BRUCE D A.Glossary of grouting terminology[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(12):1534-1542.
[3] 罗平平.裂隙岩体可灌性及灌浆数值模拟研究[D].南京:河海大学,2006.
[4]EWERT F K.Rock grouting with Emphasis on Dam Sites[M].Berlin:Springer-Verlag,1985.
[5] 马国彦,林秀山.水利水电工程灌浆与地下水排水[M].北京:中国水利水电出版社,2001.
[6] SADEGHIYEH S M,HASHEMI M,AJALLOEIAN R.Comparison of permeability and groutability of ostur dam site rock mass for grout curtain design[J].Rock Mechanics and Rock Engineering,2013,46(2):341-357.
[7] SOHRABIBIDAR A,RASTEGARNIA A,ZOLFAGHARI A.Estimation of the grout take using empirical rela⁃tionships(case study:Bakhtiari dam site)[J].Bulletin of Engineering Geology and the Environment,2016,75(2):425-438.
[8] 樊贵超,钟登华,任炳昱,等.基于分形理论的坝基裂隙岩体注灰量与导水率关系研究[J].水利学报,2017,48(5):560-567.
[9] DRAGANOVIC A,STILLE H.Filtration and penetrability of cement-based grout:Study performed with a short slot[J].Tunnelling and Underground Space Technology,2011,26(4):548-559.
[10] 杨璐,孙满利,黄建华,等.交河故城PS-C灌浆加固材料可灌性的实验室研究[J].岩土工程学报,2010,32(3):397-400.
[11] BARANI H R,LASHKARIPOUR G,GHAFOORI M.A proposal for geological groutability index(GGI)of ce⁃ment grouting in rock foundations[J].Indian Journal of Science and Technology,2014,2(7):95-103.
[12] HUDSON J.Rock engineering systems.Theory and Practice[M].Ellis Horwood Limited Publisher,1992.
[13] 陈筠,郭果.基于RES理论的潜在滑坡识别[J].工程地质学报,2014,22(3):456-463.
[14] 余伟健,高谦,韩阳,等.基于RES的地下巷道工程稳定性全耦合分析方法[J].岩土力学,2008,29(6):1489-1493.
[15] RAFIEE R,ATAEI M,KHALOOKAKAIE R.A new cavability index in block caving mines using fuzzy rock en⁃gineering system[J].International Journal of Rock Mechanics and Mining Sciences,2015,77:68-76.
[16] FARAMARZI F,MANSOURI H,FARSANGI M A E.Development of rock engineering systems-based models for flyrock risk analysis and prediction of flyrock distance in surface blasting[J].Rock Mechanics and Rock Engi⁃neering,2014,47(4):1291-1306.
[17] 李德毅,杜鹢.不确定性人工智能[M].北京:国防工业出版社,2005.
[18] 帅青燕,何亚伯.基于云模型的坝基岩体质量综合评价[J].东南大学学报:自然科学版,2013,43(S1):54-58.
[19] 魏博文,黄海鹏,徐镇凯.基于云模型和组合赋权的岩体质量二维评价模型[J].岩石力学与工程学报,2016,35(S1):3092-3099.
[20] 李健,汪明武,徐鹏,等.基于云模型的围岩稳定性分类[J].岩土工程学报,2014,36(1):83-87.
[21] 周科平,林允,胡建华,等.基于熵权—正态云模型的岩爆烈度分级预测研究[J].岩土力学,2016,37(S1):596-602.
[22] 尹超,王晓原,张敬磊,等.基于遗传算法和云模型的公路沿线泥石流灾害危险性区划[J].岩石力学与工程学报,2016,35(11):2266-2275.
[23] 张秋文,章永志,钟鸣.基于云模型的水库诱发地震风险多级模糊综合评价[J].水利学报,2014,45(1):87-95.
[24] MORTAZAVI A,MAADIKHAH A.An investigation of the effects of important grouting and rock parameters on the grouting process[J].Geomechanics and Geoengineering,2016,11(3):219-235.
[25] SAEIDI O,STILLE H,TORABI S R.Numerical and analytical analyses of the effects of different joint and grout properties on the rock mass groutability[J].Tunnelling and Underground Space Technology,2013,38:11-25.
