地震作用下混凝土坝时变动力可靠度的概率密度演化方法研究
2017-05-07陈健云贾启彬
陈健云,贾启彬,徐 强
(1.大连理工大学 工程抗震研究所,辽宁 大连 116024;
2.大连理工大学 海岸与近海工程国家重点实验室,辽宁 大连 116024)
1 研究背景
我国西部地区既是水能资源丰富的地区,也是地震频发的地区。混凝土坝在长期运行过程中不可避免地遭受各种外界环境和外部荷载的影响[1],导致坝体的抗震能力随时间逐渐退化,进而可能引起大坝在地震作用下面临溃决灾变的风险,造成人员伤亡和经济损失。所以对混凝土坝进行全寿命周期抗震安全性能评估有着重要意义[2]。
混凝土坝所处外界环境的不确定性以及大坝本身性能的变异性促使人们用可靠度方法来评价其安全性。当这些不确定性的因素同时具有时变性时,可靠度变的十分复杂且计算量巨大,因此在水工领域关于时变可靠度的研究有限。刘宁等[3]考虑了温度场、徐变应力场和混凝土强度的随机性并结合随机有限元计算了混凝土重力坝的时变可靠度;张俊芝等[4]在系统可靠度的基础上探讨了服役混凝土重力坝系统可靠度随时间的变化;杨志刚[5]应用灰色理论对随机变量时变性进行预测,同时引入了混凝土损伤变量对混凝土重力坝时变可靠性进行了分析;姜树海等[6-8]分析了大坝运行过程中各种随机变量的时变特性对大坝防洪安全和堤坝渗流风险的影响;苏怀智等[9-11]相继将信息熵理论、模糊概率理论、相关性分析、多失效模式和非概率可靠度等方法运用到了混凝土重力坝的时变可靠度分析中。上述研究均考虑了大坝服役过程中结构可靠度的变化,结合时变特性运用传统瞬时可靠度分析方法对大坝进行可靠性评价。但是由于传统可靠度方法的限制,时变可靠度的分析仅局限于有限的离散时间点。另外,抗震动力性能作为大坝服役期间一个很重要的研究对象,并未具体出现在上述研究当中。虽然也有学者[12-16]对混凝土坝随时间变化的抗震能力进行了相关研究,但是并未考虑环境及坝体自身的不确定性,缺少大坝安全的可靠性评价,所以有必要针对运行过程中坝体的抗震性能变化从概率角度进行大坝抗震安全性评价。
根据以上所述,基于李杰等[17]提出的概率密度演化理论,本文首次提出一种全寿命周期抗震性能可靠度分析方法,区别于广义概率密度演化理论中给定的初始条件,这里根据等价极值事件求得所需初始条件,并将随运行时间变化的混凝土坝动力非线性响应极值按随机过程处理建立概率密度演化方程,运用数值方法求解,基于首次超越准则对大坝进行时变动力可靠度分析。该方法可兼顾坝体结构的时变性和不确定性,与以往方法相比,本文方法充分利用概率密度演化理论在计算动力可靠度方面的高效率和高精度的优势,避免样本统计阶段带来的误差,从概率角度分析混凝土坝抗震性能随服役时间的演化规律,并给出连续时间的时变可靠度分析。经算例验证,建议方法与蒙特卡洛法对比,计算结果一致性较好,计算效率提高。
2 混凝土坝时变抗震性能概率密度演化理论
地震动作用下混凝土坝的非线性动力响应分析方程即可表示为:
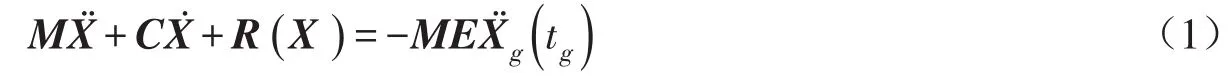
考虑材料随机性,假设Θ=(Θ1Θ2…Θs)为混凝土坝结构性能参数中的随机变量,s为混凝土坝性能参数中随机变量的个数;为混凝土坝任意感兴趣的性能指标(例如位移、应力或层面抗滑稳定系数等),m为感兴趣的性能指标的数目。则式(1)可表示为:

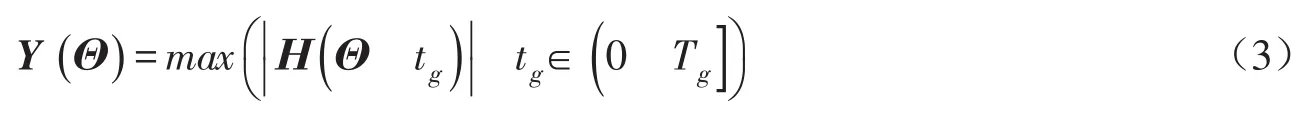
式中:Tg为给定地震动总持时。
考虑材料时变性,引入一个时间变量ta,ta∈[0Ta],其中,ta表示混凝土坝已运行时间,Ta表示混凝土坝服役期限,一般为50年到100年。则在地震作用下Z(tg)的极值。变为表示大坝运行ta时间后,
在整个服役期间内,Y(Θta)为一个保守的随机系统,所以根据概率守恒原理可得广义概率密度演化方程[17]:
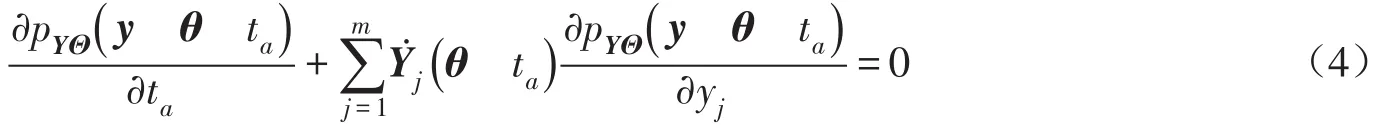
当m=1时,式(4)变成一维广义概率密度演化方程[17]:
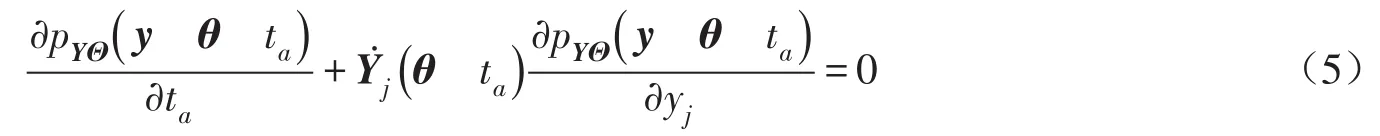
如将式(5)应用于整个大坝服役期内,还需要重新求解所需初始条件,结合等价极值事件,引入虚拟过程[18]:

这里ta=0表示混凝土坝开始投入使用,使式(6)满足如下条件:

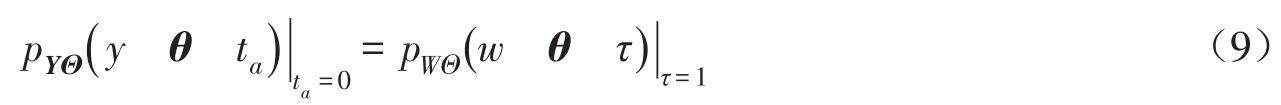
最终通过求解式(5)可以得到Y(t)即整个服役期间目标物理量的概率密度函数:

从而,可以得到结构时变动力可靠度:

式中:Ωs为未超过限值的安全区域。
通常情况下,式(5)和式(8)无法直接求得解析解,需要借助有限差分法进行求解,常用的差分格式[19]包括:单边差分格式、Lax-Wendroff格式、TVD差分格式,不同差分格式稳定性和收敛性不同,需要根据实际问题选择合适的差分格式,本文选择单边差分格式。
离散代表点的选取是概率密度演化理论的关键性技术,代表点选取的好坏将直接影响计算结果的准确性,方式众多,本文采用数论选点法并基于GF偏差对点集进行优化[20]。
3 混凝土坝地震动时变可靠度分析
3.1 基本步骤 基于概率密度演化理论的全寿命周期可靠度分析方法可分为以下几个步骤:
(1)选取坝体混凝土弹性模量和抗拉强度作为随机变量。根据分布类型和混凝土特性时变规律选取离散代表点集,其中q=1 2…Nsel为代表点集数目,ta为运行时间。基于GF偏差对点集优化,并依据voronoi区域计算赋得概率Pq。
(2)根据选取的代表点选择参数建立有限元模型,计算大坝的动力响应,得到服役期内坝体响应极值以及速率本文采用和文献[21]一致的相对位移角作为坝体响应。
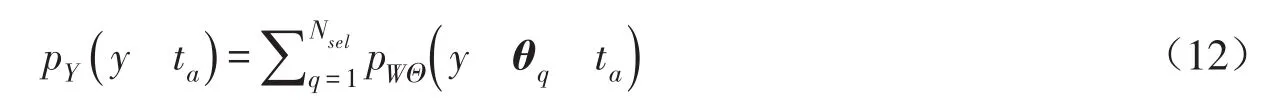
(5)根据式(11)计算服役期内结构时变动力可靠度的R(t)。
3.2 混凝土重力坝时变动力可靠度分析 针对某一混凝土重力坝,采用本文所提出的方法进行时变动力可靠度分析。大坝模型参数如图1所示,仅进行坝体分析。坝体材料参数见表1,混凝土本构模型选用开裂位移损伤模型[22]。外荷载主要考虑静力荷载(重力、水压力、扬压力、泥沙压力)和地震作用,动水压力按照Westergaard附加质量法计算。地震动选取:按照100年超越概率2%的基岩地震动水平向峰值加速度为0.304g,对Koyna实测地震波进行调幅,竖向地震动峰值取其2/3。
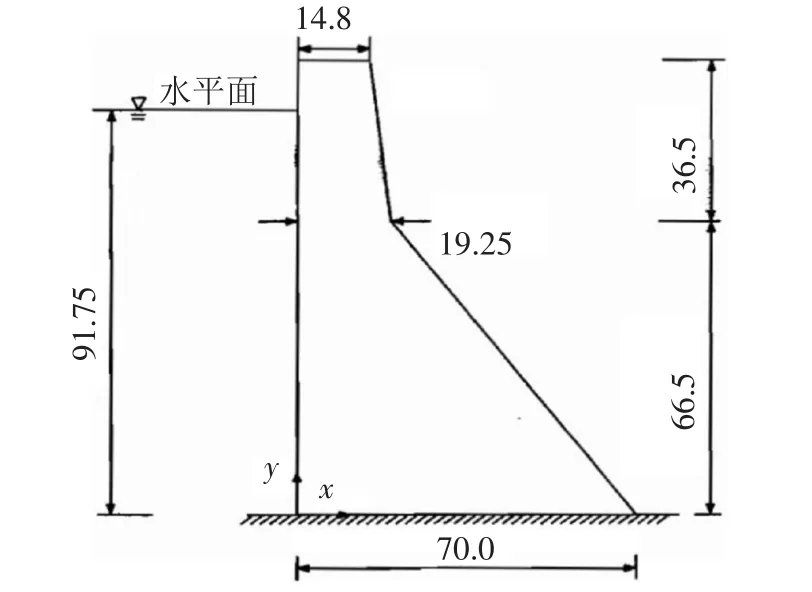
图1 大坝模型(单位:m)
3.3 随机变量选择 本文引入坝体参数不确定性和时变性分析地震作用下大坝时变动力可靠度。考虑影响混凝土坝力学性能的主要因素[23-24],选取弹性模量和混凝土强度作为随机变量,均值取表1中对应的数值,变异系数均为0.1,服从正态分布类型,选取89个样本点。对于坝体材料的时变性,经过学者们大量研究试验得到了一系列的关于混凝土的时变规律,本文参考相关文献[4,25],衰减函数取为:
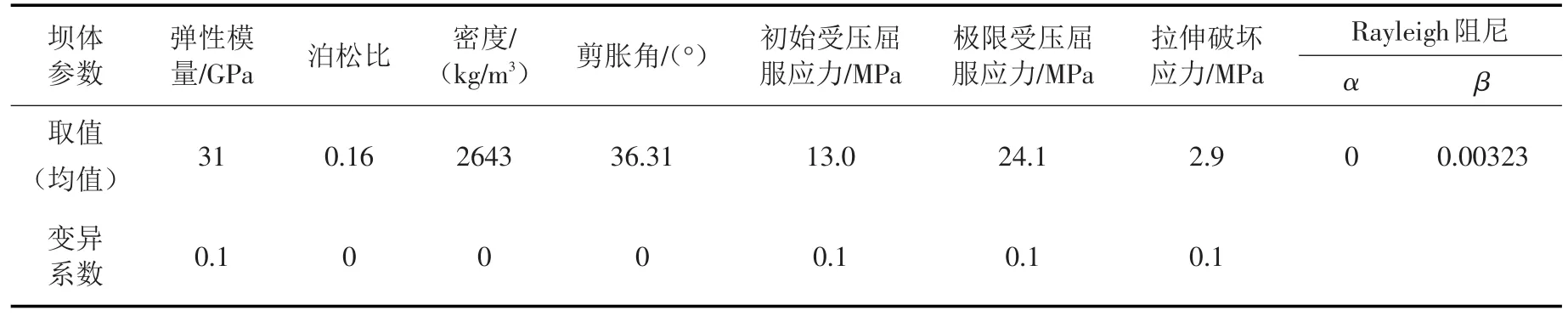
表1 材料参数
混凝土强度:

混凝土弹性模量:

式中:Rc(0)为混凝土初始强度;Ec(0)为混凝土初始弹性模块;t单位为年。
衰减规律如图2所示。
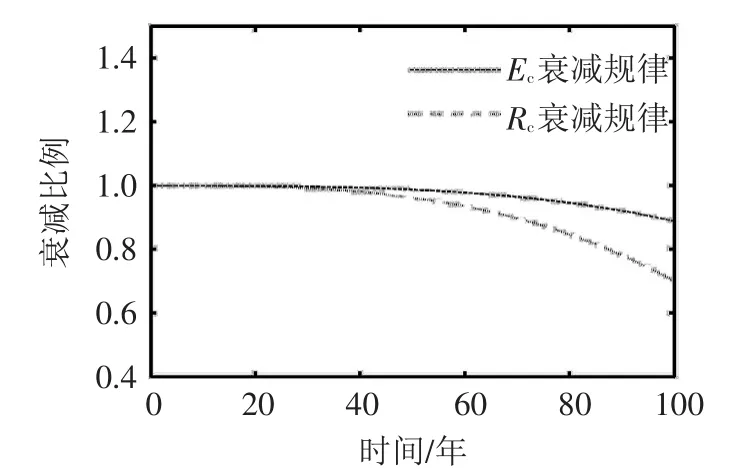
图2 衰减规律
3.4 结果分析 利用上述模型分别分析了大坝正常运行状态和地震作用下的性能变化。
3.4.1 正常运行状态 首先对正常运行状态的大坝承载能力进行分析,主要荷载包括重力、水压力、扬压力和泥沙压力。通过上游坝顶与坝踵的相对位移角φ1(t)反映坝体整体的变形和承载能力:

φ1(t)的概率信息如图3所示。从图3(a)可以发现,位移角均值变化与图2中材料参数的变化规律相似,这是因为在恒定静力外荷载下,结构处于弹性范围内,坝体相对位移角将随材料参数变化呈线性变化;从图3(b)可以看到,第1年的φ1(t)概率分布与第50年的φ1(t)概率分布差别很小,到第100年φ1(t)的均值变大,表明在运行前中期,性能退化不明显;当进入到后期,坝体进入老化阶段,性能衰减速率增加。
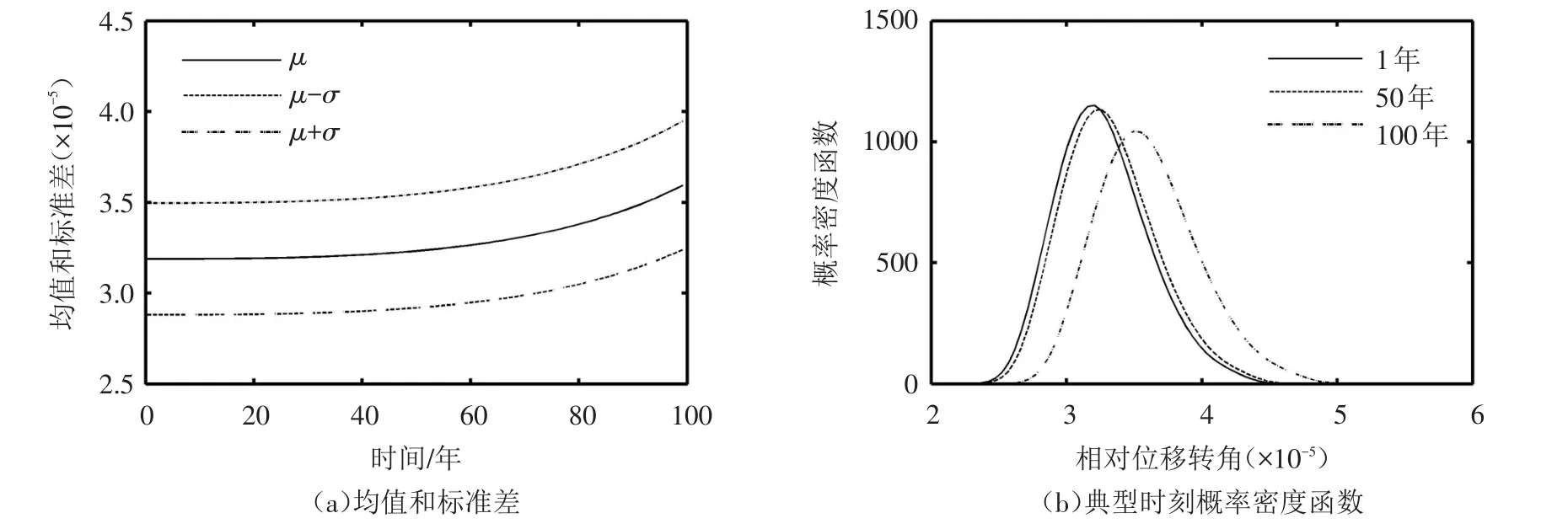
图3 正常运行状态Φ1(t)概率信息
3.4.2 地震作用下 本文考虑了在大坝服役周期过程中,随着材料逐渐退化首次遭遇地震荷载坝体的响应。根据以往的实际震害资料和学者分析研究,重力坝下游折坡处是其抗震薄弱位置,易发生开裂破坏,因此这里引入了位移角φ2(t)作为折坡处开裂程度的评价指标:

φ2(t)的概率信息如图4所示。从图4可以看到:在地震作用下,坝体材料进入非线性阶段,结构的响应变得不规则;结合图4(a)和(b)发现,φ2(t)的均值和标准差随运行时间逐渐增加,在最后30年离散性显著变大,说明坝体的加速老化使得坝体抗震性能的不确定性迅速增加,坝体抗震性能呈整体下降趋势。究其原因,坝体材料性能退化,导致其自身的振动频率降低,强度降低;地震荷载下混凝土发生损伤破坏引起刚度和强度降低,造成坝体的动力特性不断发生变化。

图4 地震作用下φ2(t)概率信息
将地震作用下的φ1(t)的概率信息提取出来,如图5所示,其概率信息的变化规律与φ2(t)的变化规律相似,两相对位移角的概率密度分布均具有极值Ⅰ型分布特征。不同的是,φ1(t)值主要分布在2×10-4~5×10-4范围内,φ2(t)值主要分布在3×10-4~8×10-4范围内,φ2(t)所反应的破坏程度高于φ1(t),表明在同样的地震作用下,下游折坡处是重力坝的脆弱部位,相较于其他位置变形要大,这与实际震害基本吻合[26],说明了可以选用相对位移角来作为评价指标。
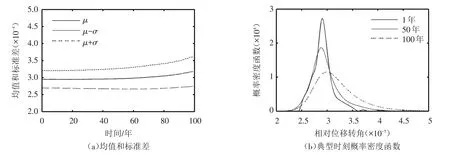
图5 地震作用下φ1(t)概率信息
3.5 时变动力可靠度分析 为便于说明本文方法,描述可靠度随时间变化规律,根据上文φ1(t)和φ2(t)的范围,分别假设φ1(t)位移角限值为3×10-4、φ2(t)位移角限值为5×10-4,计算大坝时变动力可靠度,结果如图6所示。图6(a)(b)分别为φ1(t)、φ2(t) 的累积概率分布时变曲面。图6(c)(d)为可靠度时变曲线。从图6可以看出,φ1(t)和φ2(t)的可靠度均随时间降低,说明抗震性能随时间逐渐退化。可靠度降低速度介于线性和指数之间,考虑到材料属性的指数型衰减以及地震作用非线性响应带来的不确定性,符合实际情况。
为验证本文方法的正确性,利用Monte Carlo算法产生500个样本点计算得到的结果对本方法89个样本点计算所得结果进行校核。由于Monte Carlo算法计算量庞大,为简化,这里仅提取了φ1(t)和φ2(t)分别在1年、50年和100年的可靠度计算结果(表2)。从表2可以看出,本文方法的计算结果与蒙特卡洛结果基本一致。每个样本点计算量相同,蒙特卡洛方法是本方法计算量的5倍之多,体现了概率密度演化理论的计算高精度和高效性。
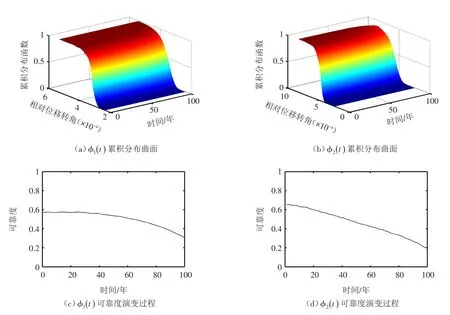
图6 大坝时变动力可靠度演化
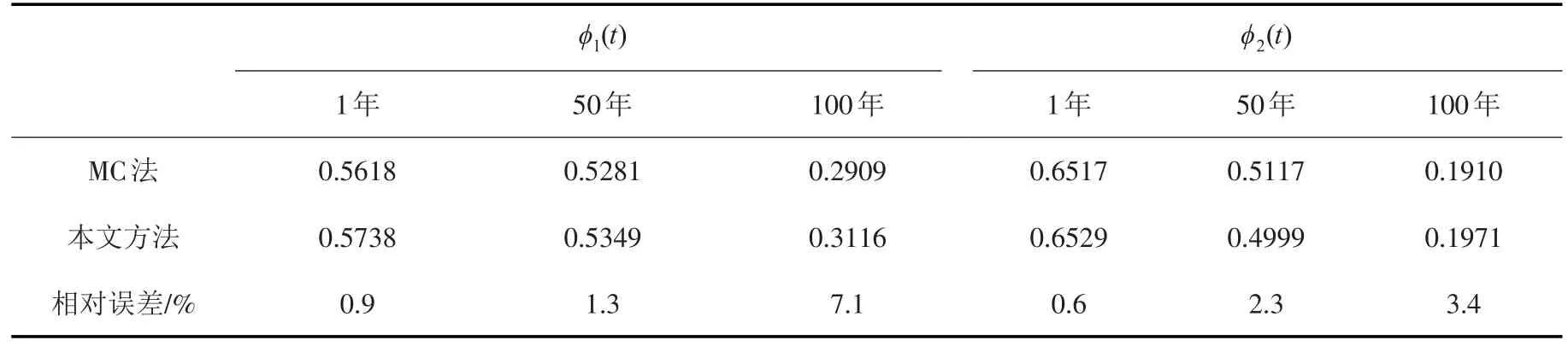
表2 数据对比
4 结论
本文针对大坝抗震性能随时间退化的现状,结合概率密度演化理论对运行过程中混凝土坝的抗震动力性能进行了概率演化分析,并经模型验证了所提出方法的可行性。本文方法兼顾了结构性能的随机性和时变性,继承了概率密度演化方法计算的高精度和高效性;跳过样本统计阶段,直接从概率密度函数角度获得了均值和标准差,避免了统计带来的误差。结果表明,该方法可以获得坝体丰富的概率演化信息和可靠度演变规律,为混凝土坝全寿命周期抗震安全评估提供了一种新思路。通过指定不同的性能评价指标(如损伤、应力、抗滑稳定系数等),可推广应用到其他结构的全寿命周期性能评估中。由于本文所使用地震波为固定的地震波,因此本文建议方法适用于确定性地震动作用下,大坝运行过程的抗震性能安全评价,所得概率结果为条件概率,考虑地震动随机性将是笔者下一步重点研究的内容。
参 考 文 献:
[1] 顾冲时,苏怀智.混凝土坝工程长效服役与风险评定研究述评[J].水利水电科技进展,2015,35(5):1-12.
[2] 张楚汉,金峰,王进廷,等.高混凝土坝抗震安全评价的关键问题与研究进展[J].水利学报,2016,47(3):253-264.
[3] 刘宁,刘光廷.随机徐变应力影响下重力坝时变可靠度初探[J].水利学报,1999(5):49-56.
[4] 张俊芝,李桂青.服役重力坝系统可靠度及概率寿命探讨[J].水利学报,2000(4):40-45.
[5] 杨志刚.基于灰色理论的混凝土重力坝损伤时变可靠度分析[D].昆明:昆明理工大学,2002.
[6] 姜树海,范子武.时变效应对大坝防洪风险率的影响研究[J].水利学报,2006,37(4):425-430.
[7] 姜树海,范子武.基于Bayes方法的堤坝时变渗流风险率评估[J].岩土工程学报,2007,29(3):420-424.
[8] 范子武,姜树海,李运辉.影响大坝防洪安全随机因子的时变特性及其量化方法[J].岩土工程学报,2008,30(11):1632-1636.
[9] SU H Z,WEN Z P,HU J,et al.Evaluation model for service life of dam based on time-varying risk probability[J].Science in China Series E:Technological Sciences,2009,52(7):1966-1973.
[10]SU H Z,HU J,WEN Z P.Service life predicting of dam systems with correlated failure modes[J].Journal of Per⁃formance of Constructed Facilities,2013,27(3):252-269.
[11] SU H Z,LI J Y,WEN Z P,et al.Dynamic non-probabilistic reliability evaluation and service life prediction for arch dams considering time-varying effects[J].Applied Mathematical Modelling,2016,40(15/16):6908-6923.
[12] GOGOI I,MAITY D.Seismic safety of aged concrete gravity dams considering fluid-structure interaction[J].Journal of Earthquake Engineering,2005,9(5):637-656.
[13]WANG J,JIN F,ZHANG C.Seismic safety of arch dams with aging effects[J].Science China Technological Sci⁃ences,2011,54(3):522-530.
[14] NAYAK P,MAITY D.Seismic damage analysis of aged concrete gravity dams[J].International Journal for Com⁃Putational Methods in Engineering Science and Mechanics,2013,14(5):424-439.
[15] 牛志国,石现春,李伟.现役混凝土坝的抗震安全分析[J].地震工程与工程振动,2014,34(S1):602-605.
[16] 王怀亮,周志宇.长期运行老化混凝土重力坝地震反应分析[J].地震工程与工程振动,2015,35(1):183-188.
[17] 李杰,陈建兵.随机动力系统中的概率密度演化方程及其研究进展[J].力学进展,2010,40(2):170-188.
[18] 陈建兵,李杰.随机结构动力可靠度分析的极值概率密度方法[J].地震工程与工程振动,2004,24(6):39-44.
[19] 陈建兵,李杰.随机结构静力反应概率密度演化方程的差分方法[J].力学季刊,2004,25(1):21-28.
[20] CHEN J,YANG J,LiI J.A GF-discrepancy for point selection in stochastic seismic response analysis of struc⁃tures with uncertain parameters[J].Structural Safety,2016,59:20-31.
[21] 刘章军,曾波,周宜红,等.地震动过程的概率模型及在重力坝抗震可靠度分析中的应用[J].水利学报,2014,45(9):1066-1074.
[22] 王金昌.ABAQUS在土木工程中的应用[M].杭州:浙江大学出版社,2006.
[23] 马怀发,陈厚群,黎保琨.混凝土试件细观结构的数值模拟[J].水利学报,2004(10):27-35.
[24] 唐欣薇,陈厚群,张楚汉.基于细观损伤力学模型的混凝土坝抗震分析[J].水力发电学报,2013,32(2):195-200.
[25] 牛荻涛.混凝土结构耐久性与寿命预测[M].北京:科学出版社,2003.
[26] 张社荣,王高辉,王超.混凝土重力坝极限抗震能力评价方法[J].水力发电学报,2013,32(3):168-175.
